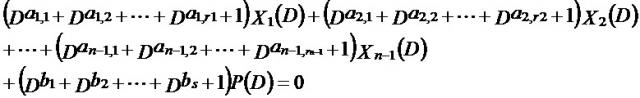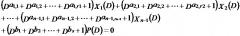2643506 - Способ кодирования, способ декодирования, кодер и декодер

Способ кодирования, способ декодирования, кодер и декодер

Иллюстрации

Показать все

Изобретение относится к вычислительной технике. Технический результат заключается в обеспечении повышенной способности к коррекции ошибок. Способ кодирования для выполнения сверхточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n, в котором принимают информационную последовательность в качестве входных данных; и кодируют информационную последовательность с использованием уравнения 1 в качестве полинома контроля по четности #g, чтобы удовлетворять 0, причем #g является g-ым порядковым номером изменяющегося во времени периода q: (уравнение 1). 4 н. и 4 з.п. ф-лы, 75 ил., 9 табл.

Реферат

Область техники, к которой относится изобретение

Настоящее изобретение относится к способу кодирования, способу декодирования, кодеру и декодеру с использованием сверточных кодов разреженного контроля по четности (LDPC-CC), поддерживающим множество скоростей кодирования.

Уровень техники

В последние годы внимание привлечено к коду разреженного контроля по четности (LDPC) в качестве кода коррекции ошибок, который предоставляет высокую способность к коррекции ошибок с осуществимым размером схем. Вследствие своей высокой способности к коррекции ошибок и простоты реализации, LDPC-код приспособлен в схеме кодирования с коррекцией ошибок для систем высокоскоростной беспроводной LAN по стандарту IEEE802.11n, систем цифровой широковещательной передачи и т.д.

LDPC-код является кодом коррекции ошибок, заданным посредством матрицы H разреженного контроля по четности. Кроме того, LDPC-код является блочным кодом, имеющим длину блока, идентичную числу столбцов N контрольной матрицы H (см. непатентный документ 1, непатентный документ 2, непатентный документ 3). Например, случайный LDPC-код, QC-LDPC-код (QC: квазициклический) предлагаются.

Тем не менее, характеристика многих современных систем связи заключается в том, что информация передачи совместно передается в расчете на пакет или кадр переменной длины, как в случае Ethernet (зарегистрированная торговая марка). Проблема с применением LDPC-кода, который является блочным кодом, к системе этого вида, например, заключается в том, как заставить кодовый LDPC-блок фиксированной длины соответствовать Ethernet-кадру (зарегистрированная торговая марка) переменной длины. IEEE802.11n применяет обработку дополнения или обработку прореживания к последовательности информации передачи и тем самым регулирует длину последовательности информации передачи и длину блока LDPC-кода. Тем не менее, трудно не допускать изменения скорости кодирования или передачи избыточной последовательности через дополнение или прореживание.

Проводятся исследования для LDPC-CC (сверточных кодов разреженного контроля по четности), допускающих выполнение кодирования или декодирования информационной последовательности произвольной длины для LDPC-кода (в дальнейшем в этом документе, он представлен посредством "LDPC-BC: блочный код разреженного контроля по четности") такого блочного кода (например, см. непатентный документ 8 и непатентный документ 9).

LDPC-CC является сверточным кодом, заданным посредством матрицы разреженного контроля по четности. Например, матрица H^T[0, n] контроля по четности LDPC-CC со скоростью кодирования R=1/2 (=b/c) показывается на фиг. 1. Здесь, элемент H^T[0, n] принимает 0 или 1.

Все элементы, отличные от , равны 0. M представляет емкость запоминающего устройства LDPC-CC, и n представляет длину кодового LDPC-CC-слова. Как показано на фиг. 1, характеристика матрицы LDPC-CC-контроля заключается в том, что она является матрицей в форме параллелограмма, в которой 1 размещается только в диагональных элементах матрицы, а соседние элементы и левый нижний и правый верхний элементы матрицы являются нулями.

LDPC-CC-кодер, заданный посредством матрицы H^T[0, n] контроля по четности, когда и , здесь представляется посредством фиг. 2. Как показано на фиг. 2, LDPC-CC-кодер формируется с помощью 2*(M+1) сдвиговых регистров с длиной c в битах и сумматора по модулю 2 (оператора "исключающее ИЛИ"). Таким образом, признак LDPC-CC-кодера заключается в том, что он может быть реализован с помощью очень простой схемы по сравнению со схемой, которая выполняет умножение порождающей матрицы, или LDPC-BC-кодера, который выполняет вычисление на основе способа обратной (прямой) подстановки.

Кроме того, поскольку кодер на фиг. 2 является кодером на основе сверточного кода, необязательно разделять информационную последовательность на блоки фиксированной длины при кодировании, и информационная последовательность любой длины может быть кодирована.

Патентный документ 1 описывает способ формирования LDPC-CC на основе полинома контроля по четности. В частности, патентный документ 1 описывает способ формирования LDPC-CC с использованием полиномов контроля по четности с изменяющимся во времени периодом 2, изменяющимся во времени периодом 3, изменяющимся во времени периодом 4 и изменяющимся во времени периодом кратным 3.

Список библиографических ссылок

Патентные документы

PTL 1.

Выложенная Патентная заявка (Япония) номер 2009-246926

Непатентные документы

NPL 1

R.G. Gallager, "Low-density parity check codes", IRE Trans. Inform. Theory, IT-8, стр. 21-28, 1962 год.

NPL 2

D.J.C. Mackay, "Good error-correcting codes based on very sparse matrices", IEEE Trans. Inform. Theory, том 45, №2, стр. 399-431, март 1999 года.

NPL 3

M.P.C. Fossorier, "Quasi-cyclic low-density parity-check codes from circulant permutation matrices", IEEE Trans. Inform. Theory, том 50, №8, стр. 1788-1793, ноябрь 2001 года.

NPL 4

M.P.C. Fossorier, M. Mihaljevic and H. Imai, "Reduced complexity iterative decoding of low density parity check codes based on belief propagation", IEEE Trans. Commun., том 47, №5, стр. 673-680, май 1999 года.

NPL 5

J. Chen, A. Dholakia, E. Eleftheriou, M.P.C. Fossorier and X.-Yu Hu, "Reduced-complexity decoding of LDPC codes", IEEE Trans. Commun., том 53, №8, стр. 1288-1299, август 2005 года.

NPL 6

J. Zhang and M.P.C. Fossorier, "Shuffled iterative decoding", IEEE Trans. Commun., том 53, №2, стр. 209-213, февраль 2005 года.

NPL 7

Стандарт IEEE для локальных вычислительных сетей и общегородских вычислительных сетей, IEEE P802.16e/D12, октябрь 2005 года.

NPL 8

A.J. Feltstrom and K.S. Zigangirov, "Time-varying periodic convolutional codes with low-density parity-check matrix", IEEE Trans. Inform. Theory, том 45, №6, стр. 2181-2191, сентябрь 1999 года.

NPL 9

R.M. Tanner, D. Sridhara, A. Sridharan, T.E. Fuja and D. J. Costello Jr., "LDPC block and convolutional codes based on circulant matrices", IEEE Trans. Inform. Theory, том 50, №12, стр. 2966-2984, декабрь 2004 года.

NPL 10

H.H. Ma and J.K. Wolf, "On tail biting convolutional codes", IEEE Trans. Commun., том com-34, №2, стр. 104-111, февраль 1986 года.

NPL 11

C. Weib, C. Bettstetter and S. Riedel, "Code construction and decoding of parallel concatenated tail-biting codes", IEEE Trans. Inform. Theory, том 47, №1, стр. 366-386, январь 2001 года.

NPL 12

M.B.S. Tavares, K.S. Zigangirov and G.P. Fettweis, "Tail-biting LDPC convolutional codes", Proc. of IEEE ISIT 2007, стр. 2341-2345, июнь 2007 года.

NPL 13

G. Muller and D. Burshtein, "Bounds on the maximum likelihood decoding error probability of low-density parity check codes", IEEE Trans. Inf. Theory, том 47, №7, стр. 2696-2710, ноябрь 2001 года.

NPL 14

R.G. Gallager, "a simple derivation of the coding theorem and some applications", IEEE Trans. Inf. Theory, том IT-11, №1, стр. 3-18, январь 1965 года.

NPL 15

A.J. Viterbi, "Error bounds for convolutional codes and the asymptotically optimum decoding algorithm", IEEE Trans. Inf. Theory, том IT-13, №2, стр. 260-269, апрель 1967 года.

NPL 16

A.J. Viterbi and J.K. Omura, "Principles of digital communication and coding", McGraw-Hill, Нью-Йорк, 1979 год.

Сущность изобретения

Техническая задача

Тем не менее, хотя патентный документ 1 описывает подробности способа формирования LDPC-CC с изменяющимися во времени периодами 2, 3 и 4 и изменяющимся во времени периодом кратным 3, изменяющиеся во времени периоды ограничены.

Следовательно, задача настоящего изобретения заключается в том, чтобы предоставить способ кодирования, способ декодирования, кодер и декодер изменяющегося во времени LDPC-CC, имеющего высокую способность к коррекции ошибок.

Решение задачи

Одним аспектом способа кодирования настоящего изобретения является способ кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем изменяющийся во времени период q является простым числом, превышающим 3, причем способ содержит прием информационной последовательности в качестве входных данных и кодирование информационной последовательности с использованием уравнения 116 в качестве g-го (g=0, 1, …, q-1) полинома контроля по четности, который удовлетворяет 0.

Одним аспектом способа кодирования настоящего изобретения является способ кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем изменяющийся во времени период q является простым числом, превышающим 3, причем способ содержит прием информационной последовательности в качестве входных данных и кодирование информационной последовательности с использованием полинома контроля по четности, который удовлетворяет:

"a_{#0, k, 1}%q=a_{#1, k, 1}%q=a_{#2, k, 1}%q=a_{#3, k, 1}%q=…=a_{#g, k, 1}%q=…=a_{#q-2, k, 1}%q=a_{#q-1, k, 1}%q=v_p=k (v_p=k: фиксированное значение)",

"b_{#0, 1}%q=b_{#1, 1}%q=b_{#2, 1}%q=b_{#3, 1}%q=…=b_{#g, 1}%q=…=b_{#q-2, 1}%q=b_{#q-1, 1}%q=w (w: фиксированное значение)",

"a_{#0, k, 2}%q=a_{#1, k, 2}%q=a_{#2, k, 2}%q=a_{#3, k, 2}%q=…=a_{#g, k, 2}%q=…=a_{#q-2, k, 2}%q=a_{#q-1, k, 2}%q=y_p=k (y_p=k: фиксированное значение)",

"b_{#0, 2}%q=b_{#1, 2}%q=b_{#2, 2}%q=b_{#3, 2}%q=…=b_{#g, 2}%q=…=b_{#q-2, 2}%q=b_{#q-1, 2}%q=z (z: фиксированное значение)", и

"a_{#0, k, 3}%q=a_{#1, k, 3}%q=a_{#2, k, 3}%q=a_{#3, k, 3}%q=…=a_{#g, k, 3}%q=…=a_{#q-2, k, 3}%q=a_{#q-1, k, 3}%q=s_p=k (s_p=k: фиксированное значение)"

g-го (g=0, 1, …, q-1) полинома контроля по четности, который удовлетворяет 0, представленного посредством уравнения 117 для k=1, 2, …, n-1.

Одним аспектом кодера настоящего изобретения является кодер, который выполняет сверточное кодирование на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), причем изменяющийся во времени период q является простым числом, превышающим 3, включающий в себя модуль формирования, который принимает информационный бит X_r[i] (r=1, 2, …, n-1) в момент времени i в качестве входных данных, обозначает уравнение, эквивалентное g-му (g=0, 1, …, q-1) полиному контроля по четности, который удовлетворяет 0, представленному посредством уравнения 116, в качестве уравнения 118 и формирует бит P[i] четности в момент времени i с использованием уравнения с подстановкой k вместо g в уравнении 118, когда i%q=k, и модуль вывода, который выводит бит P[i] четности.

Одним аспектом способа декодирования настоящего изобретения является способ декодирования, соответствующий вышеописанному способу кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q (простое число, превышающее 3) с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), для декодирования кодированной информационной последовательности, кодированной с использованием уравнения 116, в качестве g-го (g=0, 1, …, q-1) полинома контроля по четности, который удовлетворяет 0, причем способ содержит прием кодированной информационной последовательности в качестве входных данных и декодирование кодированной информационной последовательности с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 116, которое является g-ым полиномом контроля по четности, который удовлетворяет 0.

Одним аспектом декодера настоящего изобретения является декодер, соответствующий вышеописанному способу кодирования для выполнения сверточного кодирования на основе разреженного контроля по четности (LDPC-CC) с изменяющимся во времени периодом q (простое число, превышающее 3) с использованием полинома контроля по четности со скоростью кодирования (n-1)/n (где n является целым числом, равным или превышающим 2), который выполняет декодирование кодированной информационной последовательности, кодированной с использованием уравнения 116, в качестве g-го (g=0, 1, …, q-1) полинома контроля по четности, который удовлетворяет 0, включающий в себя модуль декодирования, который принимает кодированную информационную последовательность в качестве ввода и декодирует кодированную информационную последовательность с использованием доверительного распространения (BP) на основе матрицы контроля по четности, сформированной с использованием уравнения 116, которое является g-ым полиномом контроля по четности, который удовлетворяет 0.

Преимущества изобретения

Настоящее изобретение может достигать высокой способности к коррекции ошибок и тем самым может обеспечивать высокое качество данных.

Краткое описание чертежей

Фиг. 1 показывает матрицу LDPC-CC-контроля;

Фиг. 2 показывает конфигурацию LDPC-CC-кодера;

Фиг. 3 показывает пример матрицы LDPC-CC-контроля с изменяющимся во времени периодом m;

Фиг. 4A показывает полиномы контроля по четности LDPC-CC с изменяющимся во времени периодом 3 и конфигурацию матрицы H контроля по четности этого LDPC-CC;

Фиг. 4B показывает взаимосвязь элементов на основе доверительного распространения, связанных с X(D) "контрольных уравнений #1-3" на фиг. 4A;

Фиг. 4C показывает взаимосвязь элементов на основе доверительного распространения, связанных с X(D) "контрольных уравнений #1-6";

Фиг. 5 показывает матрицу контроля по четности сверточного кода (7, 5);

Фиг. 6 показывает пример конфигурации матрицы H LDPC-CC-контроля со скоростью кодирования 2/3 и изменяющимся во времени периодом 2;

Фиг. 7 показывает пример конфигурации матрицы LDPC-CC-контроля со скоростью кодирования 2/3 и изменяющимся во времени периодом m;

Фиг. 8 показывает пример конфигурации матрицы LDPC-CC-контроля со скоростью кодирования (n-1)/n и изменяющимся во времени периодом m;

Фиг. 9 показывает пример конфигурации модуля LDPC-CC-кодирования;

Фиг. 10 является блок-схемой, показывающей пример матрицы контроля по четности;

Фиг. 11 показывает пример LDPC-CC-дерева с изменяющимся во времени периодом 6;

Фиг. 12 показывает пример LDPC-CC-дерева с изменяющимся во времени периодом 6;

Фиг. 13 показывает пример конфигурации матрицы LDPC-CC-контроля со скоростью кодирования (n-1)/n и изменяющимся во времени периодом 6;

Фиг. 14 показывает пример LDPC-CC-дерева с изменяющимся во времени периодом 7;

Фиг. 15A показывает пример схемы кодера со скоростью кодирования 1/2;

Фиг. 15B показывает пример схемы кодера со скоростью кодирования 1/2;

Фиг. 15C показывает пример схемы кодера со скоростью кодирования 1/2;

Фиг. 16 показывает способ завершения нулем;

Фиг. 17 показывает пример контрольной матрицы, когда завершение нулем выполняется;

Фиг. 18A показывает пример контрольной матрицы, когда дополнение битами концевой части выполняется;

Фиг. 18B показывает пример контрольной матрицы, когда дополнение битами концевой части выполняется;

Фиг. 19 показывает общее представление системы связи;

Фиг. 20 является концептуальной схемой системы связи с использованием кодирования с коррекцией со стиранием ошибок с использованием LDPC-кода;

Фиг. 21 является схемой общей конфигурации системы связи;

Фиг. 22 показывает пример конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора;

Фиг. 23 показывает пример конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора;

Фиг. 24 показывает пример конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора;

Фиг. 25 показывает пример конфигурации кодера с коррекцией со стиранием ошибок;

Фиг. 26 является схемой общей конфигурации системы связи;

Фиг. 27 показывает пример конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора;

Фиг. 28 показывает пример конфигурации связанного с кодированием с коррекцией со стиранием ошибок процессора;

Фиг. 29 показывает пример конфигурации модуля кодирования с коррекцией со стиранием ошибок, поддерживающего множество скоростей кодирования;

Фиг. 30 показывает общее представление кодирования посредством кодера;

Фиг. 31 показывает пример конфигурации модуля кодирования с коррекцией со стиранием ошибок, поддерживающего множество скоростей кодирования;

Фиг. 32 показывает пример конфигурации модуля кодирования с коррекцией со стиранием ошибок, поддерживающего множество скоростей кодирования;

Фиг. 33 показывает пример конфигурации декодера, поддерживающего множество скоростей кодирования;

Фиг. 34 показывает пример конфигурации матрицы контроля по четности, используемой посредством декодера, поддерживающего множество скоростей кодирования;

Фиг. 35 показывает пример конфигурации пакета, когда кодирование с коррекцией со стиранием ошибок выполняется, и когда кодирование с коррекцией со стиранием ошибок не выполняется;

Фиг. 36 показывает взаимосвязь между контрольными узлами, соответствующими полиномам контроля по четности #α и #β, и переменным узлом;

Фиг. 37 показывает субматрицу, сформированную посредством извлечения только частей, связанных с X₁(D) матрицы H контроля по четности;

Фиг. 38 показывает пример LDPC-CC-дерева с изменяющимся во времени периодом 7;

Фиг. 39 показывает пример LDPC-CC-дерева с изменяющимся во времени периодом h изменяющегося во времени периода 6;

Фиг. 40 показывает BER-характеристику регулярных TV11-LDPC-CC #1, #2 и #3 в таблице 9;

Фиг. 41 показывает матрицу контроля по четности, соответствующую g-му (g=0, 1, …, h-1) полиному контроля по четности (83) со скоростью кодирования (n-1)/n и изменяющимся во времени периодом h;

Фиг. 42 показывает пример шаблона переупорядочения, когда пакеты информации и пакеты четности конфигурируются независимо;

Фиг. 43 показывает пример шаблона переупорядочения, когда пакеты информации и пакеты четности конфигурируются без различения между ними;

Фиг. 44 показывает подробности способа кодирования (способа кодирования на уровне пакета) на уровне выше физического уровня;

Фиг. 45 показывает подробности другого способа кодирования (способа кодирования на уровне пакета) на уровне выше физического уровня;

Фиг. 46 показывает пример конфигурации группы четности и субпакетов четности;

Фиг. 47 показывает способ укорачивания (способ #1-2);

Фиг. 48 показывает правило вставки в способе укорачивания (способе #1-2);

Фиг. 49 показывает взаимосвязь между позициями, в которых известная информация вставляется, и способностью к коррекции ошибок;

Фиг. 50 показывает соответствие между полиномом контроля по четности и моментами времени;

Фиг. 51 показывает способ укорачивания (способ #2-2);

Фиг. 52 показывает способ укорачивания (способ #2-4);

Фиг. 53 является блок-схемой, показывающей пример связанной с кодированием части, когда переменная скорость кодирования приспосабливается на физическом уровне;

Фиг. 54 является блок-схемой, показывающей другой пример связанной с кодированием части, когда переменная скорость кодирования приспосабливается на физическом уровне;

Фиг. 55 является блок-схемой, показывающей пример конфигурации модуля декодирования с коррекцией ошибок на физическом уровне;

Фиг. 56 показывает способ коррекции со стиранием ошибок (способ #3-1);

Фиг. 57 показывает способ коррекции со стиранием ошибок (способ #3-3);

Фиг. 58 показывает "завершение информационным нулем" LDPC-CC со скоростью кодирования (n-1)/n;

Фиг. 59 показывает способ кодирования согласно варианту 12 осуществления;

Фиг. 60 является схемой, схематично показывающей полином контроля по четности LDPC-CC со скоростями кодирования 1/2 и 2/3, который дает возможность совместного использования схемы между кодером и декодером;

Фиг. 61 является блок-схемой, показывающей пример основных компонентов кодера согласно варианту 13 осуществления;

Фиг. 62 показывает внутреннюю конфигурацию первого модуля вычисления информации;

Фиг. 63 показывает внутреннюю конфигурацию модуля вычисления четности;

Фиг. 64 показывает другой пример конфигурации кодера согласно варианту 13 осуществления;

Фиг. 65 является блок-схемой, показывающей пример основных компонентов декодера согласно варианту 13 осуществления;

Фиг. 66 иллюстрирует операции модуля задания логарифмического отношения правдоподобия в случае скорости кодирования 1/2;

Фиг. 67 иллюстрирует операции модуля задания логарифмического отношения правдоподобия в случае скорости кодирования 2/3;

Фиг. 68 показывает пример конфигурации устройства связи, содержащего кодер согласно варианту 13 осуществления;

Фиг. 69 показывает пример формата передачи; и

Фиг. 70 показывает пример конфигурации устройства связи, содержащего кодер согласно варианту 13 осуществления.

Подробное описание вариантов осуществления

Далее подробно описаны варианты осуществления настоящего изобретения со ссылкой на прилагаемые чертежи.

До описания конкретных конфигураций и операций вариантов осуществления, LDPC-CC на основе полиномов контроля по четности, описанный в патентном документе 1, сначала описывается.

LDPC-CC на основе полинома контроля по четности

Во-первых, описывается LDPC-CC с изменяющимся во времени периодом 4. Случай, в котором скорость кодирования составляет 1/2, описывается ниже в качестве примера.

Рассмотрим уравнения 1-1-1-4 в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 4. В это время, X(D) является полиномиальным представлением данных (информации), и P(D) является полиномиальным представлением четности. Здесь, в уравнениях 1-1-1-4, допускаются полиномы контроля по четности, в которых существует четыре элемента в X(D) и P(D), соответственно, при этом причина заключается в том, что четыре элемента требуются с точки зрения достижения хорошего качества приема.

[1]

… (уравнение 1-1)

… (уравнение 1-2)

… (уравнение 1-3)

… (уравнение 1-4)

В уравнении 1-1, предполагается, что a1, a2, a3 и a4 являются целыми числами (где a1≠a2≠a3≠a4 и a1-a4 взаимно отличаются). Использование системы обозначений "X≠Y≠…≠Z" предполагается, чтобы выражать тот факт, что X, Y, …, Z взаимно отличаются. Кроме того, предполагается, что b1, b2, b3 и b4 являются целыми числами (где b1≠b2≠b3≠b4). Полином контроля по четности уравнения 1-1 называется "контрольным уравнением #1", и субматрица на основе полинома контроля по четности уравнения 1-1 обозначается как первая субматрица H₁.

В уравнении 1-2, предполагается, что A1, A2, A3 и A4 являются целыми числами (где A1≠A2≠A3≠A4). Кроме того, предполагается, что B1, B2, B3 и B4 являются целыми числами (где B1≠B2≠B3≠B4). Полином контроля по четности уравнения 1-2 называется "контрольным уравнением #2", и субматрица на основе полинома контроля по четности уравнения 1-2 обозначается как вторая субматрица H₂.

В уравнении 1-3, предполагается, что α1, α2, α3 и α4 являются целыми числами (где α1≠α2≠α3≠α4). Кроме того, предполагается, что β1, β2, β3 и β4 являются целыми числами (где β1≠β2≠β3≠β4). Полином контроля по четности уравнения 1-3 называется "контрольным уравнением #3", и субматрица на основе полинома контроля по четности уравнения 1-3 обозначается как третья субматрица H₃.

В уравнении 1-4, предполагается, что E1, E2, E3 и E4 являются целыми числами (где E1≠E2≠E3≠E4). Кроме того, предполагается, что F1, F2, F3 и F4 являются целыми числами (где F1≠F2≠F3≠F4). Полином контроля по четности уравнения 1-4 называется "контрольным уравнением #4", и субматрица на основе полинома контроля по четности уравнения 1-4 обозначается как четвертая субматрица H₄.

Затем, рассмотрим LDPC-CC с изменяющимся во времени периодом 4, который формирует контрольную матрицу, как показано на фиг. 3, из первой субматрицы H₁, второй субматрицы H₂, третьей субматрицы H₃ и четвертой субматрицы H₄.

В это время, если k обозначается как остаток после деления значений комбинаций порядков X(D) и P(D), (a1, a2, a3, a4), (b1, b2, b3, b4), (A1, A2, A3, A4), (B1, B2, B3, B4), (α1, α2, α3, α4), (β1, β2, β3, β4), (E1, E2, E3, E4) и (F1, F2, F3, F4), в уравнениях 1-1-1-4 на 4, предусматривается по одному каждому из остатков 0, 1, 2 и 3, которые должны быть включены в наборы из четырех коэффициентов, представленные так, как показано выше (например, (a1, a2, a3, a4)), и является справедливым для всех вышеуказанных наборов из четырех коэффициентов.

Например, если порядки (a1, a2, a3, a4) X(D) "контрольного уравнения #1" задаются как (a1, a2, a3, a4)=(8, 7, 6, 5), остатки k после деления порядков (a1, a2, a3, a4) на 4 - это (0, 3, 2, 1), и по одному каждому из 0, 1, 2 и 3 включаются в набор из четырех коэффициентов в качестве остатков k. Аналогично, если порядки (b1, b2, b3, b4) P(D) "контрольного уравнения #1" задаются как (b1, b2, b3, b4)=(4, 3, 2, 1), остатки k после деления порядков (b1, b2, b3, b4) на 4 - это (0, 3, 2, 1), и по одному каждому из 0, 1, 2 и 3 включаются в набор из четырех коэффициентов в качестве остатков k. Предполагается, что вышеуказанное условие по "остатку" также справедливо для наборов из четырех коэффициентов X(D) и P(D) других уравнений контроля по четности ("контрольного уравнения #2", "контрольного уравнения #3" и "контрольного уравнения #4").

Посредством этого весовой коэффициент столбца матрицы H контроля по четности, сконфигурированной из уравнений 1-1-1-4, становится 4 для всех столбцов, что предоставляет возможность формирования регулярного LDPC-кода. Здесь, регулярный LDPC-код является LDPC-кодом, который задается посредством матрицы контроля по четности, для которой весовой коэффициент каждого столбца является в равной степени фиксированным, и отличается посредством того факта, что его характеристики являются стабильными, и минимальный уровень ошибки практически никогда не возникает. В частности, поскольку характеристики являются хорошими, когда весовой коэффициент столбца равняется 4, LDPC-CC, предлагающий хорошие характеристики приема, может достигаться посредством формирования LDPC-CC так, как описано выше.

Таблица 1 показывает пример LDPC-CC (LDPC-CC #1-3) с изменяющимся во времени периодом 4 и скоростью кодирования 1/2, для которого справедливо вышеуказанное условие по "остатку". В таблице 1, LDPC-CC с изменяющимся во времени периодом 4 задаются посредством четырех полиномов контроля по четности: "контрольного полинома #1", "контрольного полинома #2", "контрольного полинома #3", и "контрольного полинома #4".

Таблица 1
Код	Полином контроля по четности
LDPC-CC #1 с изменяющимся во времени периодом 4 и скоростью кодирования 1/2	Контрольный полином #1: (D⁴⁵⁸+D⁴³⁵+D³⁴¹+1)X(D)+(D⁵⁹⁸+D³⁷³+D⁶⁷+1)P(D)=0Контрольный полином #2: (D²⁸⁷+D²¹³+D¹³⁰+1)X(D)+(D⁵⁴⁵+D⁵⁴²+D¹⁰³+1)P(D)=0Контрольный полином #3: (D⁵⁵⁷+D⁴⁹⁵+D³²⁶+1)X(D)+(D⁵⁶¹+D⁵⁰²+D³⁵¹+1)P(D)=0Контрольный полином #4: (D⁴²⁶+D³²⁹+D⁹⁹+1)X(D)+(D³²¹+D⁵⁵+D⁴²+1)P(D)=0
LDPC-CC #2 с изменяющимся во времени периодом 4 и скоростью	Контрольный полином #1: (D⁵⁰³+D⁴⁵⁴+D⁴⁹+1)X(D)+(D⁵⁶⁹+D⁴⁶⁷+D⁴⁰²+1)P(D)=0Контрольный полином #2: (D⁵¹⁸+D⁴⁷³+D²⁰³+1)X(D)+(D⁵⁹⁸+D⁴⁹⁹+D¹⁴⁵+1)P(D)=0Контрольный полином #3:

кодирования 1/2

(D⁴⁰³+D³⁹⁷+D⁶²+1)X(D)+(D²⁹⁴+D²⁶⁷+D⁶⁹+1)P(D)=0Контрольный полином #4: (D⁴⁸³+D³⁸⁵+D⁹⁴+1)X(D)+(D⁴²⁶+D⁴¹⁵+D⁴¹³+1)P(D)=0

LDPC-CC #3 с изменяющимся во времени периодом 4 и скоростью кодирования 1/2

Контрольный полином #1: (D⁴⁵⁴+D⁴⁴⁷+D¹⁷+1)X(D)+(D⁴⁹⁴+D²³⁷+D⁷+1)P(D)=0Контрольный полином #2: (D⁵⁸³+D⁵⁴⁵+D⁵⁰⁶+1)X(D)+(D³²⁵+D⁷¹+D⁶⁶+1)P(D)=0Контрольный полином #3: (D⁴³⁰+D⁴²⁵+D⁴⁰⁷+1)X(D)+(D⁵⁸²+D⁴⁷+D⁴⁵+1)P(D)=0Контрольный полином #4: (D⁴³⁴+D³⁵³+D¹²⁷+1)X(D)+(D³⁴⁵+D²⁰⁷+D³⁸+1)P(D)=0

Случай для скорости кодирования 1/2 описан выше в качестве примера, но даже когда скорость кодирования составляет (n-1)/n, если вышеуказанное условие по "остатку" также справедливо для наборов из четырех коэффициентов информации X₁(D), X₂(D), …, X_n-1(D), соответственно, код является по-прежнему регулярным LDPC-кодом, и хорошее качество приема может достигаться.

В случае изменяющегося во времени периода 2, также подтверждено, что код с хорошими характеристиками может находиться, если вышеуказанное условие по "остатку" применяется. LDPC-CC с изменяющимся во времени периодом 2 с хорошими характеристиками описывается ниже. Случай, в котором скорость кодирования составляет 1/2, описывается ниже в качестве примера.

Рассмотрим уравнения 2-1 и 2-2 в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 2. В это время, X(D) является полиномиальным представлением данных (информации), и P(D) является полиномиальным представлением четности. Здесь, в уравнениях 2-1 и 2-2, допускаются полиномы контроля по четности, в которых существует четыре элемента в X(D) и P(D), соответственно, при этом причина заключается в том, что четыре элемента требуются с точки зрения достижения хорошего качества приема.

[2]

… (уравнение 2-1)

… (уравнение 2-2)

В уравнении 2-1, предполагается, что a1, a2, a3 и a4 являются целыми числами (где a1≠a2≠a3≠a4). Кроме того, предполагается, что b1, b2, b3 и b4 являются целыми числами (где b1≠b2≠b3≠b4). Полином контроля по четности уравнения 2-1 называется "контрольным уравнением #1", и субматрица на основе полинома контроля по четности уравнения 2-1 обозначается как первая субматрица H₁.

В уравнении 2-2, предполагается, что A1, A2, A3 и A4 являются целыми числами (где A1≠A2≠A3≠A4). Кроме того, предполагается, что B1, B2, B3 и B4 являются целыми числами (где B1≠B2≠B3≠B4). Полином контроля по четности уравнения 2-2 называется "контрольным уравнением #2", и субматрица на основе полинома контроля по четности уравнения 2-2 обозначается как вторая субматрица H₂.

Затем, рассмотрим LDPC-CC с изменяющимся во времени периодом 2, сформированный из первой субматрицы H₁ и второй субматрицы H₂.

В это время, если k обозначается как остаток после деления значений комбинаций порядков X(D) и P(D), (a1, a2, a3, a4), (b1, b2, b3, b4), (A1, A2, A3, A4), (B1, B2, B3, B4), в уравнениях 2-1 и 2-2 на 4, предусматривается по одному каждому из остатков 0, 1, 2 и 3, которые должны быть включены в наборы из четырех коэффициентов, представленные так, как показано выше (например, (a1, a2, a3, a4)), и является справедливым для всех вышеуказанных наборов из четырех коэффициентов.

Посредством этого весовой коэффициент столбца матрицы H контроля по четности, сконфигурированной из уравнений 2-1 и 2-2, становится 4 для всех столбцов, что предоставляет возможность формирования регулярного LDPC-кода. Здесь, регулярный LDPC-код является LDPC-кодом, который задается посредством матрицы контроля по четности, для которой весовой коэффициент каждого столбца является в равной степени фиксированным, и отличается посредством того факта, что его характеристики являются стабильными, и минимальный уровень ошибки практически никогда не возникает. В частности, поскольку характеристики являются хорошими, когда весовой коэффициент столбца равняется 8, LDPC-CC, предоставляющий возможность дополнительного улучшения характеристик приема, может достигаться посредством формирования LDPC-CC так, как описано выше.

Таблица 2 показывает примеры LDPC-CC (LDPC-CC #1 и #2) с изменяющимся во времени периодом 2 и скоростью кодирования 1/2, для которых справедливо вышеуказанное условие по "остатку". В таблице 2, LDPC-CC с изменяющимся во времени периодом 2 задаются посредством двух полиномов контроля по четности: "контрольного полинома #1" и "контрольного полинома #2".

Таблица 2
Код	Полином контроля по четности
LDPC-CC #1 с изменяющимся во времени периодом 2 и скоростью кодирования 1/2	Контрольный полином #1: (D⁵⁵¹+D⁴⁶⁵+D⁹⁸+1)X(D)+(D⁴⁰⁷+D³⁸⁶+D³⁷³+1)P(D)=0Контрольный полином #2: (D⁴⁴³+D⁴³³+D⁵⁴+1)X(D)+(D⁵⁵⁹+D⁵⁵⁷+D⁵⁴⁶+1)P(D)=0
LDPC-CC #2 с изменяющимся во времени периодом 2 и скоростью кодирования 1/2	Контрольный полином #1: (D²⁶⁵+D¹⁹⁰+D⁹⁹+1)X(D)+(D²⁹⁵+D²⁴⁶+D⁶⁹+1)P(D)=0Контрольный полином #2: (D²⁷⁵+D²²⁶+D²¹³+1)X(D)+(D²⁹⁸+D¹⁴⁷+D⁴⁵+1)P(D)=0

Выше описан случай, в котором (LDPC-CC с изменяющимся во времени периодом 2), скорость кодирования составляет 1/2 в качестве примера, но даже когда скорость кодирования составляет (n-1)/n, если вышеуказанное условие по "остатку" справедливо для наборов из четырех коэффициентов в информации X₁(D), X₂(D), …, X_n-1(D), соответственно, код является по-прежнему регулярным LDPC-кодом, и хорошее качество приема может достигаться.

В случае изменяющегося во времени периода 3, также подтверждено, что код с хорошими характеристиками может находиться, если следующее условие по "остатку" применяется. LDPC-CC с изменяющимся во времени периодом 3 с хорошими характеристиками описывается ниже. Случай, в котором скорость кодирования составляет 1/2, описывается ниже в качестве примера.

Рассмотрим уравнения 3-1-3-3 в качестве полиномов контроля по четности LDPC-CC, имеющего изменяющийся во времени период 3. В это время, X(D) является полиномиальным представлением данных (информации), и P(D) является полиномиальным представлением четности. Здесь, в уравнениях 3-1-3-3, полиномы контроля по четности допускаются так, что существует три элемента в X(D) и P(D), соответственно.

[3]

… (уравнение 3-1)

… (уравнение 3-2)

… (уравнение 3-3)

В уравнении 3-1, предполагается, что a1, a2 и a3 являются целыми числами (где a1≠a2≠a3). Кроме того, предполагается, что b1, b2 и b3 являются целыми числами (где b1≠b2≠b3). Полином контроля по четности уравнения 3-1 называется "контрольным уравнением #1", и субматрица на основе полинома контроля по четности уравнения 3-1 обозначается как первая субматрица H₁.

В уравнении 3-2, предполагается, что A1, A2 и A3 являются целыми числами (где A1≠A2≠A3). Кроме того, предполагается, что B1, B2 и B3 являются целыми числами (где B1≠B2≠B3). Полином контроля по четности уравнения 3-2 называется "контрольным уравнением #2", и субматрица на основе полинома контроля по четности уравнения 3-2 обозначается как вторая субматрица H₂.

В уравнении 3-3, предполагается, что α1, α2 и α3 являются целыми числами (где α1≠α2≠α3). Кроме того, предполагается, что β1, β2 и β3 являются целыми числами (где β1≠β2≠β3). Полином контроля по четности уравнения 3-3 называется "контрольным уравнением #3", и субматрица на основе полинома контроля по четности уравнения 3-3 обозначается как третья субматрица H₃.

Затем, рассмотрим LDPC-CC с изменяющимся во времени периодом 3, сформированный из первой субматрицы H₁, второй субматрицы H₂ и третьей субматрицы H₃.

В это время, если k обозначается как остаток после деления значений комбинаций порядков X(D) и P(D), (a1, a2, a3), (b1, b2, b3), (A1, A2, A3), (B1, B2, B3), (α1, α2, α3) и (β1, β2, β3), в уравнениях 3-1-3-3 на 3, предусматривается по одному каждому из остатков 0, 1 и 2, которые должны быть включены в наборы из трех коэффициентов, представленные так, как показано выше (например, (a1, a2, a3)), и является справедливым для всех вышеуказанных наборов из трех коэффициентов.

Например, если порядки (a1, a2, a3) X(D) "контрольного уравне

Способ кодирования, способ декодирования, кодер и декодер

Патент 2643506