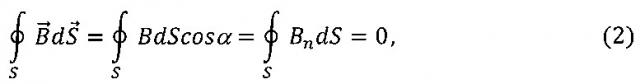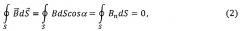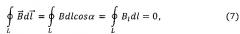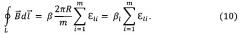Установка для решения четвёртого уравнения максвелла

Установка для решения четвёртого уравнения максвелла

Иллюстрации

Показать все

Реферат

Изобретение относится к учебным приборам и может быть использовано в лабораторном практикуме в высших и средних специальных учебных заведениях по курсу физики для изучения и углубления знаний физических законов и явлений.

Известен прибор для исследования электромагнитного поля прямолинейного проводника с током (RU патент №2170459, 20.07.2001. Бюл. №19. Автор: Ковнацкий В.К.), содержащий катушку индуктивности, подключенную к генератору переменного тока, и измерительную катушку, подключенную к измерителю ЭДС. Он позволяет исследовать электромагнитное поле и измерить ряд его характеристик. Однако на нем нельзя решить четвертое уравнение Максвелла.

Известен также измеритель проекции вектора напряженности переменного магнитного поля (RU патент №2306616, 20.09.2007. Бюл. №26. Авторы: Белокопытов Р.А., Ковнацкий В.К.), содержащий катушку индуктивности, создающую электромагнитное поле, и измеритель величин его характеристик. Однако на нем также нельзя решить четвертое уравнение Максвелла.

Наиболее близкой к предлагаемой установке является установка для исследования поля электрического и магнитного диполей (RU патент №2273056, 27.03.2006. Бюл. №9. Авторы: Белокопытов Р.А., Ковнацкий В.К.), содержащая планшет, на котором установлена неподвижная катушка индуктивности, подключенная к генератору переменного тока, и подвижная катушка индуктивности, подключенная к измерителю ЭДС. Установка позволяет проводить широкий круг исследований электромагнитного поля. Однако она не позволяет решить четвертое уравнение Максвелла.

Целью изобретения является расширение функциональных возможностей этой установки. Эта цель достигается тем, что в нее введены: штырь, установленный на подвижной катушке индуктивности перпендикулярно ее оси и планшету; контур обхода в виде окружности, изображенной на планшете, в центре которой расположена неподвижная катушка индуктивности, при этом контур обхода разбит на четное число интервалов, кратное четырем, и во всех средних точках интервалов сделаны отверстия для установки штыря подвижной катушки индуктивности; шкала расстояний, изображенная на планшете и проведенная от центра контура обхода в первую его точку, которая снабжена отверстиями для штыря подвижной катушки индуктивности и разметкой расстояния; измеритель разности фаз, первые вводы которого соединены с выводами подвижной катушки индуктивности; опорная катушка индуктивности, которая также снабжена штырем и установлена в отверстие на планшете рядом с подвижной катушкой индуктивности в окрестности первой точки контура обхода, выводы которой соединены со вторыми вводами измерителя разности фаз; указатель направления катушки, установленный на каждой катушке в торце и параллельно их осям.

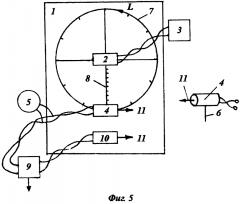
На фиг. 1, 2, 3 и 4 изображены чертежи, поясняющие принцип работы предлагаемой установки. На фиг. 5 изображен общий вид этой установки.

Предлагаемая установка содержит: 1 - планшет; 2 - неподвижная катушка индуктивности; 3 - генератор переменного тока; 4 - подвижная катушка индуктивности; 5 - измеритель ЭДС; 6 - штырь; 7 - контур обхода; 8 - шкала расстояний; 9 - измеритель разности фаз; 10 - опорная катушка индуктивности; 11 - указатель направления катушки.

Рассмотрим теоретические положения, которые легли в основу предлагаемой установки. Четвертое уравнение Максвелла в интегральной форме показывает, что магнитный поток сквозь произвольную неподвижную замкнутую поверхность, мысленно проведенную в электромагнитное поле, равен нулю.

Будем рассматривать случай, когда в центре сферической поверхности расположена неподвижная катушка индуктивности НК, создающая электромагнитное поле звуковой частоты (фиг. 1). Замкнутую сферическую поверхность S_сф можно получить вращением окружности с радиусом R вокруг оси NM неподвижной катушки индуктивности НК (фиг. 1). Поток вектора магнитной индукции сквозь эту поверхность

Непосредственное определение интеграла в выражении (1) вызывает трудности. Упростим решение этой задачи. Для этого проведем две симметричные относительно оси NM плоскости вектора , как показано на фиг. 1, отстоящие друг от друга на малом расстоянии h. В результате этого образуется также замкнутая поверхность S в виде шарового пояса с высотой h. Поток вектора через эту поверхность S

где B_n=Bcosα - проекция вектора на направление вектора , проведенного к поверхности S; α - угол между векторами и (фиг. 2).

Поток вектора сквозь шаровой пояс S равен нулю, поэтому он будет также равен нулю и через множество других шаровых поясов, которые можно получить вращением окружности с радиусом R вокруг оси NM (фиг. 1). Следовательно, будет равен нулю и поток вектор сквозь всю сферическую поверхность S_сф, определяемою формулой (1).

Так как вектор шарового пояса S всюду параллелен его основаниям, поэтому интегрирование выражения B_ndS в формуле (2) следует проводить только по его боковой поверхности. Разобьем боковую поверхность шарового пояса S на прямоугольники с высотой h и основанием dl, площадь которых dS=hdl (фиг. 1). Это позволяет перейти от интегрирования по поверхности шарового пояса S к интегрированию по его профилю L=2πR:

Для определения интеграла в формуле (3) численным методом заменим точную формулу ее приближением:

где B_ni - проекция вектора на направление нормали , проведенную в i-ю точку контура L; Δl_i - i-й отрезок контура L. Принимаем все отрезки одинаковой длины, тогда Δl_i=Δl.

Для определения B_ni разбиваем контур L на m равных частей, тогда Δl=2πR/m. На фиг. 2 показан случай, когда m=12. Образующиеся точки отрезков нумеруем против часовой стрелки (i=1, 2, 12). В каждой i-й точке проводим нормали к замкнутому контуру L.

Величины B_ni в i-x точках определяем индукционным методом с помощью подвижной катушки индуктивности ПК и подключенного к ней измерителя ЭДС (вольтметра V с большим входным сопротивлением) по следующей формуле:

где β - постоянный коэффициент; ε_ni - измеряемая вольтметром в i-ой точке ЭДС; ν - частота переменного магнитного поля; ω - число витков и S_k - площадь поперечного сечения подвижной катушки индуктивности ПК.

Подставим выражение (5) в формулу (4), тогда получим окончательное выражение для определения потока вектора :

Из выражения (6) видно, что для определения потока вектора магнитной индукции сквозь замкнутую поверхность шарового пояса S необходимо разбить контур L на m равных частей. Измерить ЭДС ε_ni в каждой i-й точке контура, вычислить сумму всех m значений ЭДС ε_ni, взятых с соответствующими знаками, и умножить на постоянный коэффициент β_n. Следует отметить, что подвижную катушку ПК устанавливаем по направлению нормали (фиг. 2).

Знаки перед ε_ni определяем следующим образом. Если в произвольной i-й точке угол α≤90°, то проекция B_ni положительная и знак перед ε_ni - положительный, если угол α>90°, то проекция B_ni отрицательная и знак перед ε_ni - отрицательный. Знаки проекций определяем экспериментальным путем с помощью измерителя разности фаз ИРФ между ЭДС опорной ОК и подвижной ПК катушками индуктивности. Знаки ЭДС показываем в каждой i-й точке контура обхода L.

Величина m должна быть четным числом, кратным четырем, тогда сумма ЭДС в формуле (6) всегда равна нулю, поэтому величины площадей dS=hdl не имеют значения. Опыт показывает, что разбиение контура обхода L на m=12 частей достаточно для требуемой точности определения потока вектора через поверхность S шарового пояса.

Предлагаемая установка позволяет определить циркуляцию вектора магнитной индукции . Если замкнутый контур L охватывает неподвижную катушку индуктивности НК, как показано на фиг. 3, то алгебраическая сумма токов K витков неподвижной катушки НК равна нулю, тогда циркуляция вектора

где B_l=Bcosα - проекция вектора на направление вектора (фиг. 4); α - угол между векторами и . Если в произвольной i-й точке угол α≤90°, то проекция B_li положительная, если угол α>90°, то проекция B_li отрицательная. Знаки проекций определяем также с помощью измерителя разности фаз между ЭДС подвижной ПК и опорной ОК катушками индуктивности. Знаки ЭДС также показываем в каждой i-й точке контура обхода L (фиг. 4).

Заменим интеграл (7) конечной суммой

где B_li - проекция вектора на направление вектора в i-й точке; Δl_i - элементы контура конечной длины, соответствующие i-й точке. Элементы контура Δl_i выбираем одинаковой длины Δl_i=Δl=2πR/m, где - четное число, кратное четырем. Рассмотрим случай m=12.

Проекции B_li в произвольных i-х точках определяем индуктивным методом с помощью подвижной катушки индуктивности ПК с подключенным к ней вольтметром с большим входным сопротивлением по следующей формуле:

где β - постоянный коэффициент, определяемый по формуле (5); ε_li - измеряемая вольтметром ЭДС.

Подставляя формулу (9) в выражение (8), получим окончательное выражение для определения циркуляции вектора :

Из выражения (10) видно, что для определения циркуляции вектора замкнутый контур L необходимо разбить на m равных частей. Измерить ЭДС ε_li каждой i-й точке контура, вычислить сумму всех m значений ЭДС ε_li, взятых с соответствующими знаками, и умножить на постоянный коэффициент β_l. Сумма ЭДС всегда равна нулю, если контур L охватывает неподвижную катушку индуктивности НК, содержащую K витков. Поэтому величина Δl и вид контура не имеют значения. В рассматриваемом случае выбираем в качестве контура L окружность, длина которой L=2πR, и разбиваем ее на 12 равных частей (m=12). Следует отметить, что подвижную катушку индуктивности ПК в каждой i-й точке устанавливаем по направлению вектора (фиг. 4).

В предлагаемой лабораторной установке применяем две одинаковые катушки индуктивности неподвижную НК и подвижную ПК. Через неподвижную катушку индуктивности НК протекает ток с частотой ν и амплитудой I, тогда

На данной установке можно определить зависимость взаимной индуктивности двух катушек L₂₁ от расстояния между ними по формуле:

где ε - ЭДС взаимоиндукции, наводимая в подвижной катушке индуктивности ПК.

Зависимость взаимной индукции L₂₁ от расстояния r до центра неподвижной катушки индуктивности НК можно снять, передвигая подвижную катушку ПК относительно неподвижной катушки НК при наличии и отсутствии сердечников в обеих катушках. Поворачивая подвижную катушку ПК относительно неподвижной катушки НК, можно убедиться в зависимости L₂₁ от ориентации катушек в пространстве.

В каждой i-й точке окружности с радиусом R можно получить экспериментальное значение нормальной B_ni и касательной B_li составляющих вектора и рассчитать их величины соответственно по формулам (5) и (9). Модуль вектора в i-й точке рассчитываем по формуле:

Экспериментально полученные значения B_i можно сравнить со значениями, полученными по теоретической формуле:

Здесь μ₀ - магнитная постоянная, μ - магнитная проницаемость сердечника неподвижной катушки НК; I - ток, протекающий через катушку НК; r₀ - радиус катушки НК; ϕ_i - угол между осью катушки НК и направляем на i-ю точку, расположенную на окружности с радиусом R.

Данная установка позволяет определить магнитную проницаемость μ среды. Для этого, меняя положение подвижной катушки ПК в точках j=1, 2, …, n, измеряем ЭДС ε_j. Затем извлекаем из неподвижной НК и подвижной ПК катушек сердечники и измеряем в тех же точках ЭДС ε_0j. По формуле

определяем магнитную проницаемость среды. Значение μ_j будут отличаться друг от друга, поэтому находим их среднее значение.

Если в произвольной точке установить подвижную катушку ПК параллельно неподвижной катушке НК, то можно измерить максимальную ЭДС ε_lmax. Затем, поворачивая подвижную катушку ПК относительно неподвижной катушки НК на угол ϕ от 0° до 360°, измеряем ЭДС ε_li. По формуле

рассчитываем пеленгационную характеристику.

Схема установки для решения четвертого уравнения Максвелла представлена на фиг. 5. Она содержит планшет 1, на котором установлена неподвижная катушка индуктивности 2, подключенная к генератору переменного тока 3, и подвижная катушка индуктивности 4, подключенная к измерителю ЭДС 5. На подвижной катушке индуктивности 4 установлен штырь 6 перпендикулярно ее оси и планшету 1.

На планшете 1 изображен контур обхода 7 в виде окружности, в центре которой расположена неподвижная катушка индуктивности 2. Окружность разбита на четное число интервалов, кратное четырем, и в средних точках интервалов сделаны отверстия для установки штыря 6 подвижной катушки индуктивности 4 и пронумерованы. На фиг. 5 для примера показан случай, когда окружность разбита на 12 равных интервалов. От центра контура обхода 7 до первой точки контура обхода 7 на планшете 1 изображена шкала расстояний 8, снабженная отверстиями для штыря 6 подвижной катушки индуктивности 4 и разметкой расстояний, начиная от центра контура обхода 7.

Для определения знака проекций вектора магнитной индукции установка содержит измеритель разности фаз 9, первые вводы которого соединены с выводами подвижной катушки индуктивности 4.

В отверстие на планшете 1 установлена своим штырем опорная катушка индуктивности 10 рядом с подвижной катушкой индуктивности 4 в окрестности первой точки контура обхода 7. Выводы ее соединены со вторыми вводами измерителя разности фаз 9.

Подвижная катушка индуктивности 4 и опорная катушка индуктивности 10 снабжены указателями направления катушки 11, которые установлены на каждой катушке в торце и параллельно их осям.

Рассмотрим, каким образом решается четвертое уравнение Максвелла, то есть как находится поток вектора магнитной индукции сквозь замкнутую поверхность шарового пояса, который должен быть равен нулю. Будем считать, что генератор переменного тока 3 включен и неподвижная катушка индуктивности 2 создает магнитное поле.

В отверстие первой точки контура обхода 7 устанавливаем с помощью штыря 6 подвижную катушку индуктивности 4, а рядом с ней устанавливаем опорную катушку индуктивности 10. При этом указатель направлений 11 катушек устанавливаем по направлению от центра по радиусу контура обхода 7. Далее опорная катушка индуктивности 10 остается на месте в окрестности первой точки контура обхода 7, а подвижную катушку индуктивности 4 последовательно устанавливаем в точки (i=1, 2, …, 12). В каждой i-й точке измеряем ЭДС ε_ni с помощью измерителя ЭДС 5. С измерителя разности фаз 9 снимаем напряжение. Если знак напряжения положительный, то ЭДС ε_ni присваиваем знак плюс, если знак напряжения отрицательный, то ЭДС ε_ni присваиваем знак минус.

В соответствии с формулой (6) суммируем все ЭДС и умножаем на постоянный коэффициент. Результат с высокой точностью должен быть равен нулю, что подтверждает четвертое уравнение Максвелла: поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю.

Рассмотрим, каким образом на данной установке определяется циркуляция вектора магнитной индукции, если контур обхода 7 охватывает неподвижную катушку индуктивности 2, и убеждаемся, что она равна нулю. Будем также считать, что генератор переменного тока 3 включен и неподвижная катушка индуктивности 2 создает магнитное поле. В отверстие первой точки контура обхода 7 устанавливаем с помощью штыря 6 подвижную катушку индуктивности 4, а рядом с ней опорную катушку индуктивности 10. При этом указатели направлений 11 катушек устанавливаем перпендикулярно радиусу контура обхода 7 по направлению стрелки контура обхода, как показано на фиг. 5.

Далее опорная катушка индуктивности 10 остается на месте в окрестности первой точки контура обхода 7, а подвижную катушку индуктивности 4 последовательно устанавливаем в точках (i=1, 2, …, 12) и измеряем ЭДС ε_li. Затем вычисляем сумму значений ЭДС ε_li, взятых с соответствующими знаками, определяемыми на измерителе разности фаз 9, и умножаем на постоянный коэффициент по формуле (10). Убеждаемся, что циркуляция вектора магнитной индукции с высокой точностью равна нулю.

Рассмотрим, каким образом определяется взаимная индуктивность L₂₁ неподвижной катушки индуктивности 2 и подвижной катушки индуктивности 4 и зависимость ее от расстояния r по шкале расстояний 8. В первую точку шкалы расстояний 8 устанавливаем подвижную катушку индуктивности 4 параллельно неподвижной катушке индуктивности 2. Меняя положение подвижной катушки индуктивности 4 в точках j=1, 2, …, n, определяем измерителем ЭДС 5 величину ЭДС ε. По формуле (12) рассчитываем величину взаимной индуктивности L₂₁ в j-х точках шкалы расстояний 8.

Модуль вектора магнитной индукции B_i в произвольной i-й точке контура обхода 7 определяем следующим образом. Сначала устанавливаем подвижную катушку индуктивности 4 в i-ю точку так, чтобы указатель направления ее 11 был направлен по направлению вектора , снимаем показания с измерителя ЭДС 5 и рассчитываем по формуле (5) величину B_ni. Затем, поворачиваем подвижную катушку индуктивности 4 так, чтобы указатель направления ее 11 был направлен по направлению вектора , снимаем показания с измерителя ЭДС 5 и рассчитываем по формуле (9) величину B_li. И, наконец, по формуле (13) определяем модуль вектора магнитной индукции B_i в i-ой точке и сравниваем его величину со значением B_i, полученным по теоретической формуле (14).

На предлагаемой установке определяется магнитная проницаемость μ среды следующим образом. В начальную точку шкалы расстояний 8 устанавливаем подвижную катушку индуктивности 4 параллельно неподвижной катушке индуктивности 2. С помощью измерителя ЭДС 5 определяем ЭДС в этой точке. Меняя положение подвижной катушки индуктивности 4 в точках j=1, 2, …, n, измеряем ЭДС ε_j. Затем извлекаем из неподвижной 2 и подвижной катушки индуктивности 4 сердечники и в тех же точках измеряем ЭДС ε_0j. По формуле (15) определяем магнитную проницаемость среды μ в этих точках. Значения μ будут отличаться друг от друга, поэтому находим среднее значение n измерений.

Рассмотрим, каким образом снимается пеленгационная характеристика. Если в произвольной точке шкалы расстояний 8 установить подвижную катушку индуктивности 4 параллельно неподвижной катушке индуктивности 2, то получим максимальное значение ЭДС ε_lmax. Затем, устанавливая подвижную катушку индуктивности 4 на угол ϕ от 0° до 360°, получаем значение ЭДС ε_li. И, наконец, по формуле (16) рассчитываем пеленгационную характеристику.

Установка для решения четвертого уравнения Максвелла, содержащая планшет, на котором установлена неподвижная катушка индуктивности, подключенная к генератору переменного тока, и подвижная катушка индуктивности, подключенная к измерителю ЭДС, отличающаяся тем, что в нее введены штырь, установленный на подвижной катушке индуктивности перпендикулярно ее оси и планшету, контур обхода в виде окружности, изображенной на планшете, в центре которой расположена неподвижная катушка индуктивности, при этом контур обхода разбит на четное число интервалов, кратное четырем, и в средних точках интервалов сделаны отверстия для установки штыря подвижной катушки индуктивности, шкала расстояний, изображенная на планшете и направленная от центра контура обхода в первую его точку, которая снабжена отверстиями для штыря подвижной катушки индуктивности и разметкой расстояния, измеритель разности фаз, первые вводы которого соединены с выводами подвижной катушки индуктивности, опорная катушка индуктивности, которая также снабжена штырем и установлена в отверстие на планшете рядом с подвижной катушкой индуктивности в окрестности первой точки контура обхода, выводы которой соединены со вторыми вводами измерителя разности фаз, указатель направления катушки, установленный на каждой катушке в торце и параллельно их осям.