Способ определения координат источника радиоизлучения с использованием летательного аппарата

Способ определения координат источника радиоизлучения с использованием летательного аппарата

Иллюстрации

Показать все

Реферат

Изобретение относится к радиотехнике, а именно к способам определения местоположения источника радиоизлучения (ИРИ), и может быть использовано в навигационных, пеленгационных, локационных средствах определения местоположения ИРИ с летательного аппарата (ЛА), в частности с беспилотного ЛА.

Известен разностно-энергетический способ определения координат местоположения ИРИ [1]. Для реализации данного способа последовательно выполняют следующие этапы:

размещают три стационарных измерителя амплитуд напряженностей электрического поля (АНЭП) в точках с известными координатами, не на одной прямой, один из которых принимают за базовый, а два оставшихся за периферийные;

измеряют и усредняют значения уровней АНЭП, создаваемых ИРИ в каждом измерителе;

передают на базовый измеритель значения АНЭП двух периферийных измерителей;

вычисляют три значения отношений попарных АНЭП, полученных в базовом и двух периферийных измерителях;

составляют три уравнения окружностей с центрами, соответствующими координатам измерителей, и радиусами обратно пропорциональными отношениям попарных АНЭП;

на основе полученных квадратов отношений попарных АНЭП и вычисленных квадратов расстояний между измерителями составляют определитель Кели-Мегнера, по которому определяют действительные расстояния от постов до ИРИ;

по любым двум, из трех возможных, парам уравнений окружностей положения ИРИ определяют текущие значения широты и долготы местоположения ИРИ.

Недостатками аналога [1] являются:

длительное время определения координат ИРИ, связанное с необходимостью циркуляции информации между стационарными измерителями;

низкая точность определения координат ИРИ, объясняемая отсутствием учета высоты ИРИ и отсутствием учета высот измерителей,

возникновением неоднозначности определения координат ИРИ, поскольку они в результате пересечения двух окружностей положения ИРИ, а те, в свою очередь, пересекаются, в общем случае, в двух точках.

Известен разностно-дальномерный способ определения координат ИРИ [2]. Для реализации данного способа последовательно выполняют следующие этапы:

размещают четыре стационарных измерителя времени приема радиосигнала ИРИ в точках с известными координатами, не на одной плоскости, один из которых принимают за базовый, а три оставшихся за периферийные;

формируют три измерительные базы измерителей, выбирая базовый измеритель, и, поочередно, один из трех периферийных;

выбирают систему единого времени во всех четырех стационарных измерителях;

принимают и запоминают время приема радиосигнала ИРИ в каждом измерителе;

передают на базовый измеритель значения времени приема радиосигнала ИРИ в каждом из трех периферийных измерителей;

вычисляют три независимые разности времени приема радиосигналов парами измерителей, образующих измерительные базы;

строят три поверхности положения ИРИ на основе каждого значения разности времени и известных координат измерителей;

вычисляют искомые координаты ИРИ как координаты точки пересечения трех поверхностей положения ИРИ.

К недостаткам аналога [2] относят:

высокую стоимость устройства, реализующего способ, обусловленную необходимостью наличия четырех измерителей времени, высокой степенью сложности антенных систем измерителей времени и их коммутационных элементов;

длительное время определения координат ИРИ, связанное с необходимостью циркуляции информации между базовым и периферийными стационарными измерителями.

Из известных способов наиболее близким аналогом (прототипом) предлагаемого способа по технической сущности является способ определения координат ИРИ [3], заключающийся в том, что:

выбирают 2-мерную декартову систему координат (ДСК) для производства измерений и расчетов;

размещают измеритель на ЛА;

перемещают указанный ЛА в пространстве;

принимают радиосигнал ИРИ в заданной полосе частот ∆F;

измеряют и запоминают первичные координатно-информативные параметры принятого радиосигнала, в качестве которых используют АНЭП, создаваемую ИРИ в точке приема;

измеряют и запоминают вторичные параметры (ВП) - координаты местоположения ЛА;

определяют пространственную ориентацию ЛА;

определяют разность фаз сигнала в антенных элементах измерителя, размещенного на ЛА;

грубо определяют направление прихода оцениваемого сигнала относительно ЛА;

многократно измеряют и запоминают совокупности АНЭП E_m (где m=1…М) и ВП x_m, у_m в М(М≥4) точках в процессе перемещения ЛА;

корректируют направление перемещения ЛА на каждой m-й точке измерений;

выбирают опорную совокупность АНЭП и ВП, например первую;

формируют пары совокупностей АНЭП и ВП, выбирая опорную и, поочередно, остальные совокупности АНЭП и ВП;

вычисляют коэффициенты окружностей Аполлония как отношения АНЭП для каждой сформированной пары совокупностей АНЭП и ВП;

формируют окружности Аполлония на основе коэффициентов окружностей Аполлония и соответствующих ВП;

в качестве координат ИРИ в 2-мерном пространстве принимают координаты точки пересечения М-1 указанных окружностей Аполлония.

Недостатками способа прототипа являются:

относительно невысокая точность определения координат ИРИ, обусловленная отсутствием учета высоты ИРИ, а также высот ЛА при измерениях АНЭП и ВП;

длительное время определения координат ИРИ, связанное с необходимостью определения пространственной ориентации ЛА, а также необходимостью корректировки полета ЛА при определении координат каждого ИРИ;

высокая стоимость устройства, реализующего способ, обусловленная необходимостью использования радиопеленгатора для предварительного грубого определения направления на ИРИ относительно ЛА.

Целью изобретения является разработка способа с более высокой точностью определения координат ИРИ в пространстве на основе формирования сферических поверхностей положения (СПП) ИРИ путем построения и последующего вращения окружностей Аполлония вокруг осей, соединяющих соответствующие фокусы. При этом фокусы окружностей Аполлония соответствуют точкам расположения ЛА в 3-мерном пространстве в различные моменты времени.

Поставленная цель достигается тем, что в известном способе определения координат ИРИ, включающем выбор ДСК для производства измерений и расчетов, размещение измерителя АНЭП на ЛА, который перемещают в пространстве, прием радиосигнала ИРИ в заданной полосе частот ΔF, измерение и запоминание первичного координатно-информативного параметра принятого радиосигнала, в качестве которого используют АНЭП, создаваемую ИРИ в точке приема, одновременное измерение и запоминание ВП - координат ЛА, измерение и запоминание М совокупностей АНЭП и ВП в процессе перемещения ЛА, выделение в качестве опорной g-й, где g=1, 2, …, M, АНЭП, формирование М-1 отличающихся друг от друга пар АНЭП, одним из элементов в каждой паре выбирают g-ю опорную АНЭП, вычисление коэффициента окружности Аполлония используя отношения АНЭП для каждой сформированной пары АНЭП, формирование окружностей Аполлония на основе коэффициентов окружностей Аполлония и соответствующих ВП, вычисление координаты ИРИ, используя окружности Аполлония, в качестве ДСК выбирают 3-мерную ДСК. ЛА перемещают в пространстве по произвольной траектории, при этом измеряют и запоминают N≥5 АНЭП E_n, где n=1…N. Одновременно измеряют и запоминают ВП - координаты ЛА в 3-мерной ДСК x_n, у_n и z_n. Вычисляют N-1 коэффициентов окружностей Аполлония как отношений АНЭП, перемноженных на обратные отношения высот ЛА в соответствующих точках измерения. По вычисленным коэффициентам окружностей Аполлония формируют N-1 СПП ИРИ путем построения и последующего вращения окружностей Аполлония вокруг осей, соединяющих соответствующие фокусы. В качестве координат ИРИ в пространстве принимают координаты точки пересечения N-1 указанных СПП ИРИ.

Благодаря перечисленной новой совокупности существенных признаков, за счет формирования СПП ИРИ путем построения и последующего вращения окружностей Аполлония вокруг осей, соединяющих соответствующие фокусы, достигается цель изобретения: повышение точности определения координат ИРИ в 3-мерном пространстве в условиях наложения ограничений на массогабаритные параметры измерительной аппаратуры, размещенной на ЛА.

Заявленный способ поясняется чертежами, на которых показаны:

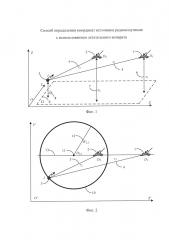
на фиг. 1 - геометрическая основа системы измерения первичных координатно-информативных параметров обнаруженных радиосигналов;

на фиг. 2 - порядок построения линии положения ИРИ - окружности Аполлония;

на фиг. 3 - порядок построения сферической поверхности положения ИРИ, за счет вращения окружности Аполлония вокруг оси, соединяющей ее фокусы.

Сущность предлагаемого способа состоит в следующем. Полагают, что объект измерений, стационарный ИРИ, излучает радиосигналы в известной полосе частот ΔF. Подвижный измеритель, размещенный на ЛА, осуществляет прием радиосигналов согласованным с ними трактом.

Геометрическая основа системы измерения первичных координатно-информативных параметров радиосигналов, в качестве которых используют АНЭП, отображена на фиг. 1, которая включает: 3-мерную ДСК OXYZ, выбранную так, чтобы плоскость OXY совпадала с поверхностью земли Ω 9 (см. фиг. 1), а ось OZ - направлена вверх; две точки нахождения ЛА D₁ 1 (см. фиг. 1) и D₂ 2 (см. фиг. 1) с измеренными ВП - координатами (х₁; у₁; z₁) и (х₂; у₂; z₂) в моменты времени t₁ и t₂; ИРИ I 3 (см. фиг. 1), координаты которого (x_и; у_и; z_и) необходимо определить.

На фиг. 1 обозначены расстояния от D₁ и D₂ до I как r₁ 4 (см. фиг. 1) и r₂ 5 (см. фиг. 1) соответственно, а также высоты ЛА в моменты времени t₁ и t₂ и высота ИРИ, отсчитываемые от поверхности земли Ω, которые в выбранной системе координат равны z₁ 6 (см. фиг. 1), z₂ 7 (см. фиг. 1) z_и 8 (см. фиг. 1) соответственно.

Используя измеренные АНЭП и ВП в двух положениях ЛА D₁ и D₂ возможно построения линии положения ИРИ - окружности Аполлония.

Для построения окружности Аполлония 10 (см. фиг. 2) вводят вспомогательную 2-мерную ДСК O’X’Y’ (см. фиг. 2) в плоскости, которая включает точки I, D₁ и D₂.

Аналитическая интерпретация алгоритма построения окружности Аполлония раскрыта в приложении А, которая сводится к нахождению в ДСК O’X’Y’ значений абсциссы а’_2,1 и ординаты b’_2,1 центра О_2,1 11 (см. фиг. 2) и значения радиуса R’_2,1 12 (см. фиг. 2).

Полученная окружность Аполлония с фокусами в точках D₁ и D₂, представляет собой набор точек, обладающих общим свойством, выражающимся в том, что при нахождении в любой этой точке указанной окружности ИРИ I коэффициент окружности Аполлония k_2,1 будет одинаковым. Следовательно, наличие этой окружности снижает неопределенность нахождения ИРИ I. Для последующего нахождения координат строят вторую окружность Аполлония, наличие которой сводит неоднозначность определения координат ИРИ до двух точек (две окружности в общем случае пересекаются в двух точках). Полностью устраняет неоднозначность наличие третьей окружности Аполлония.

Возможность определения координат ИРИ на основе 4-х измерений и построения 3-х окружностей Аполлония показана в способе-прототипе. Однако, при решении задачи в 3-х мерном пространстве, в общем случае высоты I, D₁, и D₂ не равны друг другу, а координаты ИРИ I априорно неизвестны, поэтому не представляется возможным выбор плоскости, образованной точками I, D₁, и D₂, и выбрать 2-мерную ДСК O’X’Y’.

В заявленном способе, для условий, когда высота ЛА от измерения к измерению существенно меняется, а высота ИРИ - произвольная, для повышения точности определения координат ИРИ, предложено использованине СПП ИРИ, построенных вращением окружностей Аполлония вокруг осей, соединяющих соответствующие фокусы. При этом фокусы окружностей Аполлония соответствуют точкам расположения ЛА в 3-мерном пространстве в различные моменты времени.

Аналитическая интерпретация алгоритма построения СПП ИРИ, за счет вращения окружности Аполлония вокруг оси, соединяющей ее фокусы раскрыта в приложении Б, которая сводится к нахождению в системе координат OXYZ значений абсциссы a_2,1, ординаты b_2,1 и аппликата с_2,1 центра O_2,1 и значения радиуса R_2,1 13 (см. фиг. 3) окружности Аполлония.

Полученная СПП ИРИ 14 (см. фиг. 3), образованная вращением окружности Аполлония 10 вокруг оси D₁D₂ 15 (см. фиг. 3), представляет собой набор точек, повторяющих свойство точек окружности Аполлония, выражающееся в том, что при нахождении в любой этой точке этой СПП коэффициент k_2,1 окружности Аполлония будет одинаковым. Наличие одной СПП ИРИ приводит к неоднозначности относительно координат ИРИ, выражающейся набором точек, образующих данную СПП ИРИ.

Для последующего устранения неоднозначности определения координат ИРИ I последовательно выполняют следующие процедуры алгоритма.

1. Перемещают в пространстве по свободной траектории ЛА в точку приема D₃. Принимают радиосигнал ИРИ в заданной полосе частот ∆F. Измеряют и запоминают АНЭП Е₃ в точке приема. Измеряют и запоминают ВП - координаты ЛА (х₃, у₃; z₃).

По аналогии с алгоритмом, раскрытым в приложении Б, получают вторую СПП ИРИ, образованную вращением окружности Аполлония вокруг оси D₁D₃. Аналитическое выражение (В.1), соответствующее второй СПП ИРИ, приведено в приложении В.

Наличие второй СПП ИРИ снижает неоднозначность относительно координат ИРИ до набора точек, образующих окружность, так как две сферы, в общем случае, пересекаются по окружности.

2. Перемещают в пространстве по свободной траектории ЛА в точку приема D₄. Принимают радиосигнал ИРИ в заданной полосе частот ΔF. Измеряют и запоминают АНЭП Е₄ в точке приема. Измеряют и запоминают ВП - координаты ЛА (х₄; у₄; z₄).

По аналогии с алгоритмом, раскрытым в приложении Б, получают третью СПП ИРИ, образованную вращением окружности Аполлония вокруг оси D₁D₄. Аналитическое выражение (В.2), соответствующее третьей СПП ИРИ приведено в приложении В.

Наличие третьей СПП ИРИ снижает неоднозначность относительно координат ИРИ до двух точек, так как три сферы, в общем случае, пересекаются в двух точках.

3. Перемещают в пространстве по свободной траектории ЛА в точку приема D₅. Принимают радиосигнал ИРИ в заданной полосе частот ∆F. Измеряют и запоминают АНЭП Е₅ в точке приема. Измеряют и запоминают ВП - координаты ЛА (х₅; у₅; z₅).

По аналогии с алгоритмом, раскрытым в приложении Б, получают уравнение четвертой СПП ИРИ, образованной вращением окружности Аполлония вокруг оси D₁D₅. Аналитическое выражение (В.3), соответствующее четвертой СПП ИРИ, приведено в приложении В.

Наличие четвертой СПП ИРИ полностью устраняет неоднозначность относительно координат ИРИ, так как четыре сферы в общем случае пересекаются в одной точке.

Таким образом, заключают, что минимально необходимое количество измерений АНЭП для определения координат ИРИ равно пяти, тогда возможно построение четырех СПП ИРИ. Однако, в общем случае, существует возможность проведения N≥5 АНЭП и формирования N-1 СПП ИРИ. При этом точность определения координат ИРИ за счет избыточности независимых измерений будет возрастать, а время, затрачиваемое на определение координат ИРИ, будет увеличиваться.

При перемещении в пространстве по свободной траектории ЛА от одной точки приема к другой решают противоречивую задачу: с одной стороны - расстояние между точками приема необходимо увеличивать для повышения точности определения координат ИРИ, с другой стороны - такое расстояние необходимо уменьшать, для сокращения времени необходимого для определения координат ИРИ. Целесообразным представляется выбор расстояния между точками приема в интервале от двух до пяти км.

В рассмотренном примере в качестве опорной выбирают первую АНЭП. В качестве опорной возможен выбор любой g-й, где g=1, 2, …, М, АНЭП. При этом суть настоящего изобретения не изменяется.

В аналитической интерпретации алгоритм нахождения точки пересечения четырех СПП ИРИ, образованных вращением окружностей Аполлония вокруг осей, соединяющих соответствующие фокусы, сводят к решению системы уравнений (В.4). Алгоритм решения такой системы, выходными параметрами которого являются координаты ИРИ х_и, у_и и z_и, также представлен в приложении В.

Дополнительно повышают точность определения координат ИРИ за счет избыточности измерений. Так как указанные измерения уровней сигнала производят в разное время, в разных условиях, точность измерения данных параметров в разных точках будет различна, а сами измерения можно считать независимыми. На основе проведенных измерений составляют (число всех различных сочетаний из 2 по N) уравнений типа (Б.4), количество которых рассчитывают по формуле:

Таким образом дополнительно строят СПП ИРИ. Данное обстоятельство позволяет повысить точность определения координат ИРИ, при этом порядок реализации описанного в приложении В итерационного алгоритма не изменяют.

Реализация заявленного способа целесообразна при использовании в качестве ЛА - беспилотного летательного аппарата, поскольку стоимость его проектирования, изготовления и эксплуатация значительно ниже аналогичной стоимости пилотируемых ЛА.

Имитационное моделирование заявленного способа определения координат ИРИ показало повышение точности определения координат ИРИ по сравнению со способом-прототипом на 10…40% (в зависимости от высоты ИРИ и высот ЛА в точках измерения), при решении задачи в 3-мерном пространстве без усложнения аппаратуры измерителя АНЭП, его реализующего.

Источники информации:

1. Патент RU №2505835, опубл. 27.01.2014. Бюл. №3.

2. Патент RU №2309420, опубл. 27.10.2007. Бюл. №30.

3. Патент RU №2510044, опубл. 20.03.2014. Бюл. №8.

Приложение А

Аналитическая интерпретация алгоритма построения линии положения ИРИ - окружности Аполлония

АНЭП Е_пр в точке приема, в соответствии с квадратичной формулой Введенского, равна:

где Р_и - мощность радиосигнала на выходе радиопередатчика ИРИ, G_и и G_пр - коэффициенты усиления антенн ИРИ и приемника (в разах) соответственно; λ - длина волны радиосигнала, r - расстояние между ИРИ и приемником, h_и и h_пр - высоты антенн ИРИ и приемника соответственно.

Для построения окружности Аполлония вводят декартову систему координат O’X’Y’ (см. фиг. 2) в плоскости, которая включает точки I, D₁ и D₂.

Полагают, что в системе координат O’X’Y’ точки D₁, и D₂ имеют следующие декартовы координаты: (х’₁; у’₁) и (х’₂; у’₂) соответственно. Тогда выражение (А.1) расчета амплитуд напряженности поля Е₁ и Е₂ в точках приема для каждого из двух положений ЛА записывают в виде:

где z₁, z₂ и z_и - высоты ЛА в моменты времени t₁ и t₂ и высота ИРИ, отсчитываемые от поверхности земли Ω, (х’_и; у’_и), - неизвестные координаты ИРИ в системе координат O’X’Y’.

Разделив правые и левые части уравнения (А.3) на правые и левые части уравнения системы (А.2), приняв в качестве допущения то, что коэффициенты усиления антенны ИРИ в направлении на D₁ и D₂ равны между собой (такое допущение справедливо в случае, когда антенна ИРИ ненаправленная, а также в случае, когда расстояния r₁ и r₃ велики по сравнению с расстояниями между D₁ и D₂), получают:

где k_2,1 - введенный коэффициент окружности Аполлония, который можно определить на основе измеренных амплитуд напряженности поля Е₁ и Е₂ и высот ЛА z₁ и z₂ в точках приема для каждого из двух положений ЛА.

Уравнение (А.4) после арифметических преобразований представляется уравнением окружности Аполлония 10 (см. фиг. 1):

где а’_2,1, b’_2,1 - абсцисса и ордината центра, a - радиус окружности Аполлония, которые, в свою очередь, равны:

Приложение Б

Аналитическая интерпретация алгоритма построения СПП ИРИ, за счет вращения окружности Аполлония вокруг оси, соединяющей ее фокусы

Полагают, что в системе координат OXYZ, точки D₁, и D₂ имеют следующие измеренные декартовы координаты: (х₁; у₁; z₁) и (х₂; у₂; z₂) соответственно. Тогда выражение (А.1) для каждого из двух положений ЛА записывают в виде:

где (х_и; у_и; z_и) - неизвестные координаты ИРИ в системе координат OXYZ.

Разделив правые и левые части уравнения (Б.2) на правые и левые части уравнения системы (Б.1), получают:

Уравнение (Б.3) после арифметических преобразований представляется уравнением СПП ИРИ 14 (см. фиг. 3), образованной вращением окружности Аполлония 10 вокруг оси D₁D₂:

где a_2,1, b_2,1, с_2,1 - абсцисса, ордината и аппликата центра, a R_2,1 - радиус СПП ИРИ, которые, в свою очередь, равны:

Приложение В

Аналитическая интерпретация алгоритма построения четырех СПП ИРИ и нахождения точки их пересечения

По аналогии с уравнением (Б.4), полученным в приложении Б выводят аналитические выражения для второй, третьей и четвертой СПП ИРИ, образованными вращением окружностей Аполлония вокруг осей, соединяющих соответствующие фокусы:

где а3,1, b3,1, с3,1 - абсцисса, ордината и аппликата центра второй СПП ИРИ,

a_4,1, b_4,1, c_4,1 - абсцисса, ордината и аппликата центра третьей СПП ИРИ,

a_5,1, b_5,1, c_5,1 - абсцисса, ордината и аппликата центра четвертой СПП ИРИ,

R_3,1, R_4,1, R_5,1 - радиусы второй, третьей и четвертой СПП ИРИ, которые, в свою очередь, равны:

где - введенные коэффициенты окружностей Аполлония.

Полученные выражения (Б.4), (B.1), (В.2) и (В.3) образуют систему уравнений:

Для решения системы уравнений (В.4) применяют следующий итерационный алгоритм, включающий следующие этапы.

Этап 1. Задают произвольные, но для быстрой сходимости наиболее правдоподобные опорные координаты ИРИ I х’_и, у’_и, z’_и.

Этап 2. Определяют значения функций и системы уравнений (В.4) в точке с координатами х’_и, у’_и, z’_и:

Этап 3. Рассчитывают невязки n_2,1, n_3,1, n_4,1 и n_5,1 по формулам

Этап 4. Составляют систему уравнений на основе разложений функций и в ряды Тейлора с точностью до первых производных:

где Δх, Δу, Δz - неизвестные значения приращений соответствующих координат требуемых для минимизации невязок.

Частные производные в выбранной опорной точке равны:

Этап 5. Решают систему уравнений (В.5), с помощью метода наименьших квадратов, для чего предварительно записывают ее в матричной форме:

где - вектор столбец искомых приращений соответствующих координат, - вектор столбец невязок соответственно «Т» - знак транспонирования вектора (матрицы),

- матрица частных производных функций и , в точке с координатами х’_и, у’_и, z’_и.

Обе части уравнения (В.6) умножают на транспонированную матрицу системы A^T:

Затем обе части уравнения (В.7) умножают на матрицу (А^ТА)^-1. Если эта матрица существует, то система определена.

С учетом того, что (A^TA)^-1A^TA=Е - единичная матрица, получают решение системы уравнений (В.6) в следующем матричном виде:

Этап 6. Определяют новые опорные координаты ИРИ I х", у" и z":

Этапы 1…6 в совокупности образуют первую итерацию. Далее итерации повторяют, используя каждый раз новые опорные координаты ИРИ I, полученные на этапе 6 предыдущей итерации. Количество необходимых итераций L зависит от корректности выбора начальных опорных координаты (этап 1) и требуемой точности определения координат ИРИ. С точностью связан шаг итерации d_L, определяемый как расстояние между точками с текущими опорными координатами ИРИ и предыдущими опорными координатами ИРИ. Шаг итерации сравнивают с предварительно заданным порогом. По результатам сравнения принимают решение: если шаг итерации больше порога - производят следующую итерацию, если меньше - завершают алгоритм. Необходимое число итераций для решения задачи координатометрии по определению координат ИРИ, как правило, не превышает четырех.

При завершении итераций в качестве координат ИРИ х_и, у_и и z_и выбирают значения опорных координат на последней итерации, которые являются выходными результатами представленного алгоритма.

1. Способ определения координат источника радиоизлучения (ИРИ) с использованием летательного аппарата (ЛА), заключающийся в том, что выбирают декартову систему координат (ДСК) для производства измерений и расчетов, размещают измеритель амплитуды напряженности электрического поля (АНЭП) на летательном аппарате (ЛА), который перемещают в пространстве, принимают радиосигнал ИРИ в заданной полосе частот ΔF, измеряют и запоминают первичный координатно-информативный параметр принятого радиосигнала, в качестве которого используют АНЭП, создаваемую ИРИ в точке приема, одновременно измеряют и запоминают вторичные параметры (ВП) - координаты ЛА, измеряют и запоминают М совокупностей АНЭП и ВП в процессе перемещения ЛА, выделяют в качестве опорной g-ю, где g=1, 2, …, M, АНЭП, формируют М-1 отличающихся друг от друга пар АНЭП, одним из элементов в каждой из пар выбирают g-ю опорную АНЭП, для каждой сформированной пары АНЭП вычисляют коэффициент окружности Аполлония, используя отношения АНЭП, на основе коэффициентов окружностей Аполлония и соответствующих ВП формируют окружности Аполлония, используя которые вычисляют координаты ИРИ, отличающийся тем, что в качестве ДСК выбирают 3-мерную ДСК, а ЛА перемещают в пространстве по произвольной траектории, при этом измеряют и запоминают N≥5 АНЭП E_n, где n=1…N, одновременно измеряют и запоминают ВП - координаты ЛА в 3-мерной ДСК x_n, у_n и z_n, вычисляют N-1 коэффициентов окружностей Аполлония как отношений АНЭП, перемноженных на обратные отношения высот ЛА в соответствующих точках измерения, по вычисленным коэффициентам окружностей Аполлония формируют N-1 сферических поверхностей положения (СПП) ИРИ путем построения и последующего вращения окружностей Аполлония вокруг осей, соединяющих соответствующие фокусы, а в качестве координат ИРИ в пространстве принимают координаты точки пересечения N-1 указанных СПП ИРИ.

2. Способ по п. 1, отличающийся тем, что в качестве ЛА используют беспилотный летательный аппарат.