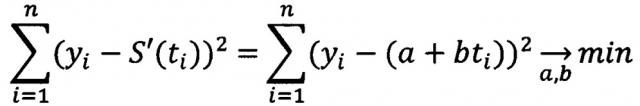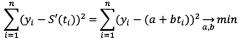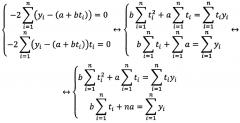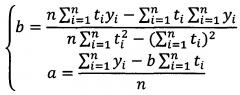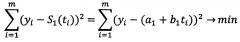Способ выделения тренда нестационарного процесса с адаптацией интервалов аппроксимации

Способ выделения тренда нестационарного процесса с адаптацией интервалов аппроксимации

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области вычислительной техники и может быть использовано в системах управления и обработки сигналов, в частности в системах цифровой обработки сигнала, в работе систем управления и контроля, при обработке сигналов в системах автоматического управления, в расчетах при выделении тенденции развития каких-либо показателей и принятии решения об удалении результатов воздействия случайных факторов.

Пусть имеется временной ряд, который представляет собой последовательность полученных в равностоящие моменты времени t₁, t₂, …, t_n n значений y₁, у₂, …, y_n (где y_i=y(t_i), i=1, 2…, n) некоторой функции y=y(t), описывающей на интервале времени t₁…t_n единственную реализацию нестационарного процесса.

Рассматриваемый процесс состоит из аддитивной смеси некоторой систематической составляющей S(t), представляющей собой полезный сигнал, или тренд, и случайной составляющей u(t), представляющей собой шум или помехи: y(t)=S(t)+u(t).

Относительно случайной составляющей u(t) предполагаем, что математическое ожидание M_u(t)=0, дисперсия D_u(t)=σ² и значения u(t) в разные моменты времени некоррелированы (cov(ut,us)=0, t≠s). Тренд S(t) в общем случае является квазидетерминированным сигналом, который рассматривается как некоторый нестационарный процесс, аналитическое описание которого неизвестно.

Основная задача - выделение полезного сигнала (тренда) в условиях недостаточной априорной информации о статистических свойствах аддитивного шума и о виде функции полезного сигнала при наличии единственной дискретной реализации исследуемого нестационарного процесса. Априорно считается, что на некоторых не слишком малых интервалах времени функция S(t) может быть достаточно точно аппроксимирована полиномом низкой степени.

Известен способ выделения тренда, заключающийся в аппроксимации дискретной реализации y₁, y₂, …, y_n исследуемого процесса функцией S'(t) путем использования метода наименьших квадратов, минимизирующего невязку . Здесь S'(t) - простая аппроксимирующая функция, которая на интервале времени [t₁; t_n] хорошо аппроксимирует полезный сигнал S(t) (Бендат Дж., Пирсол А. Прикладной анализ случайных данных: пер. с англ. – М.: Мир, 1989, стр. 114). Например, для линейной зависимости S'(t)=a+bt параметры a, b определяют из условия минимизации суммы квадратов отклонений элементов ряда y₁, y₂, …, y_n исследуемого процесса от значений полинома S'(t) в соответствующих точках t_i, т.е. из условия

Дифференцируя данное выражение по a и b и приравнивая их к нулю, получают систему линейных уравнений:

Решая полученную систему уравнений, определяют значения коэффициентов аппроксимации:

Недостатком описанного способа является вычислительная сложность выделения полезного сигнала. Это обусловлено тем, что при применении способа к сложным сигналам большой продолжительности, описываемым временным рядом с большим числом членов n, использование простых аппроксимирующих функций невозможно, а применение сложных функций с большим числом параметров, например полиномов высокой степени, резко увеличивает вычислительную сложность. При больших объемах выборки и отсутствии априорной информации о статистических свойствах случайного шума и модели полезного сигнала вместо полиномов высокой степени используют также кусочную аппроксимацию нестационарного процесса простыми функциями на коротких интервалах, но это тоже увеличивает вычислительную сложность способа.

Наиболее близким к предлагаемому изобретению по технической сущности и достигаемому результату (прототипом) является способ выделения тренда путем размножения оценок его единственной исходной реализации (РАЗОЦ) и устройство для его осуществления, заключающийся в том, что единственную дискретную реализацию нестационарного процесса, представляющую сумму полезного сигнала и шума, последовательно разбивают на интервалы, на каждом из которых осуществляют аппроксимацию методом наименьших квадратов. При этом исходную реализацию нестационарного случайного процесса предварительно разбивают на интервалы с помощью генератора случайных чисел, распределенных по равномерному закону, последующую упомянутую аппроксимацию исходной реализации нестационарного случайного процесса производят на каждом из упомянутых интервалов, разбиение на интервалы повторяют заданное число раз, затем последовательно в каждом промежутке разбиения исходной дискретной реализации нестационарного случайного процесса получают оценки тренда полезного сигнала, после чего по методу среднего арифметического усредняют полученные оценки тренда (патент RU №2207622, МПК G06F 17/18, опубл. 2003).

Недостатком описанного способа является повышенная вычислительная сложность процесса выделения полезного сигнала (тренда), обусловленная тем, что отсутствие адаптации числа и протяженности интервалов разбиения к динамике поведения сигнала приводит к необходимости разбиения реализации сигнала на большое число интервалов, причем процесс разбиения и процедура аппроксимации на каждом из интервалов должна повторяться многократно.

Предлагаемым способом решается техническая проблема уменьшения вычислительной сложности процесса выделения тренда.

Для достижения технического результата в способе выделения тренда нестационарного процесса с адаптацией интервалов аппроксимации, заключающемся в том, что единственную дискретную реализацию нестационарного процесса, представляющую сумму полезного сигнала и шума, последовательно разбивают на интервалы, на каждом из которых осуществляют аппроксимацию методом наименьших квадратов, ширину первого интервала выбирают равной части от общей продолжительности единственной дискретной реализации, выполняют аппроксимацию данного интервала и, если невязка аппроксимации превышает заданное значение, аппроксимацию повторяют, задавая ширину интервала равной части ее предыдущего значения, для каждого последующего интервала задают ширину, равную значению на предыдущем интервале, выполняют аппроксимацию и, если получают невязку аппроксимации меньше заданного значения установленное число раз подряд, увеличивают ширину последующего интервала, а если получают невязку аппроксимации больше заданного значения, то ширину текущего интервала выбирают равной части ее имеющегося значения и повторяют аппроксимацию, причем если ширина последнего интервала выходит за пределы единственной дискретной реализации нестационарного процесса, то ширину этого интервала ограничивают шириной оставшегося неаппроксимированного интервала.

Уменьшение вычислительной сложности процесса выделения полезного сигнала (тренда) вследствие сокращения или исключения многократного повторения аппроксимации исходной реализации заданным полиномом на всех интервалах и использованием на участках с различной шириной спектра интервалы с близкой к оптимальной протяженностью достигается за счет того, что ширину первого интервала выбирают равной части от общей продолжительности единственной дискретной реализации, выполняют аппроксимацию данного интервала и, если невязка аппроксимации превышает заданное значение, аппроксимацию повторяют, задавая ширину интервала равной части ее предыдущего значения, для каждого последующего интервала задают ширину, равную значению на предыдущем интервале, выполняют аппроксимацию и, если получают невязку аппроксимации меньше заданного значения установленное число раз подряд, увеличивают ширину последующего интервала, а если получают невязку аппроксимации больше заданного значения, то ширину текущего интервала выбирают равной части ее имеющегося значения и повторяют аппроксимацию, причем если ширина последнего интервала выходит за пределы единственной дискретной реализации нестационарного процесса, то ширину этого интервала ограничивают шириной оставшегося неаппроксимированного интервала.

Предлагаемый способ выделения тренда нестационарного процесса с адаптацией интервалов аппроксимации осуществляется следующим образом.

Изначально имеется наличие единственной дискретной реализации исследуемого нестационарного процесса y₁, y₂, …, y_n, где y_i=y(t_i), i=1, 2, …, n, представляющего сумму полезного сигнала (тренда) и шума, т.е. y(t)=S(t)+u(t). Априорная информация об исследуемом процессе заключается в том, что на некоторых интервалах Δ_j⊂[t₁, t_n] полезный сигнал (тренд) достаточно точно описывается полиномом, где Δ_j=[t_j-1, t_j], j⊂[1, n]. Для описания способа считают, что степень полинома равна единице, т.е. S(t)=a+bt, хотя в общем случае это может быть самая произвольная функция.

Рассматриваемый способ содержит следующие шаги:

Шаг 0:

Определяют число входящих в первый аппроксимируемый интервал членов ряда m=int(n*k₀), где функция int возвращает целое значение от аргумента, а коэффициент k₀, лежащий на интервале (0, 1), определяют из динамических свойств исходного сигнала, например из ширины спектра исходного сигнала f_max: чем шире спектр, тем меньше величина k₀ и в соответствии с теоремой Найквиста k₀=(t_n-t₁)/[2f_max]. Если сведения об f_max отсутствуют, то полагаем k₀=0,5.

Если m=n, то берут k₀=k₀*k₀ и повторяют шаг 0.

Задают величину невязки ε, определяющую требуемую точность соответствия выделенного тренда имеющейся дискретной реализации. Очевидно, ее значение не должно быть меньше среднеквадратического отклонения шумовой составляющей u(t).

Шаг 1:

Запоминают первый отрезок исходного ряда {y_i}, где i=1, …m;

Методом наименьших квадратов осуществляют аппроксимацию элементов ряда y₁, y₂, …, y_m полиномом первой степени: S₁(t)=a₁+b₁t.

Коэффициенты a₁, b₁ аппроксимирующего полинома S₁(t)=a₁+b₁t определяют из условия минимизации суммы квадратов отклонений элементов ряда y₁, y₂, …, y_m от значений полинома S₁(t) в соответствующих точках, т.е. из условия

Для нахождения соответствующих данному условию значений коэффициентов a₁, b₁ используют формулы

Находят невязку ε₁ аппроксимирующей функции S₁(t_i) на первом интервале ряда {y_i}, где i=1, …, m, по формуле . Если невязка ε₁>ε, то задают m=int(m*k₁) и повторяют шаг 1 для нового значения m, где величину k₁ выбирают из соображений скорости адаптации ширины интервала аппроксимации к характеру изменения динамики полезного сигнала (оптимально, если k₁ лежит в пределах от 0,5 до 0,8). Если невязка ε₁≤ε, то фиксируют индекс последнего члена рассмотренного ряда r=m, задают число аппроксимаций без повторного пересчета p=0, номер следующего интервала j=2 и переходят к шагу 2.

Шаг 2:

Если на очередном шаге окажется, что m+r>n, то задают m=n-r и рассматривают очередные m членов ряда {y_i}, где i=r+1, r+2, …, r+m, r - индекс, заданный на предыдущем шаге. Методом наименьших квадратов аппроксимируют элементы ряда y_r+1, y_r+2, …, y_r+m полиномом первой степени: S_j(t)=a_j+b_jt.

Из условия минимума суммы квадратов отклонений находят коэффициенты a_j, b_j аппроксимирующего полинома j-го интервала, дополнительно используя условие, необходимое для непрерывности ломаной аппроксимирующей функции S_j(t_r)=S_j-1(t_r), откуда следует a_j=a_j-1+(b_j-1-b_j)t_r. Находят невязку ε_j аппроксимирующей функции S_j(t_i) на отрезке ряда {y_i}, где i=r+1, …, r+m, по формуле . Если невязка ε_j>ε, то полагают p=0, задают m=int(m*k₁) и повторяют шаг 2 с r+1 новым значением m. Если невязка ε_j≤ε, то сохраняют значения a_j, b_j, фиксируют индекс последнего члена рассмотренного ряда r=r+m, подсчитывают число "удачных", не требующих повторного пересчета из-за невыполнения условия ε_j≤ε аппроксимаций p=p+1, и, если p превышает заданное число, например 3, полагают p=0 и увеличивают ширину последующего аппроксимируемого интервала m по формуле m=int(m*k₂), где величину k₂ выбирают из тех же соображений, что и k₁ (оптимально, если k₂ лежит в пределах от 1.2 до 2.0, или, например, k₂=1/k₁). Задают r=r+m и, если r<n, инкрементируют номер интервала j=j+1 и переходят к началу шага 2.

Если функция полезного сигнала (тренда) достаточно точно описывается полиномом заданной степени на некотором интервале и динамические свойства полезного сигнала (тренда) не изменяются на протяжении всей дискретной реализации исследуемого нестационарного процесса, то ширина всех интервалов будет равна ширине, выбранной на первом шаге. Следовательно, вычислительная сложность реализации способа уменьшается, так как существенно сокращается число повторного выполнения процедуры аппроксимации методом наименьших квадратов. Кроме того, способ обладает свойством адаптивности, благодаря которому протяженность и число интервалов оптимизируют, когда динамика изменения полезного сигнала (тренда) на очередном шаге отличается от его динамических свойств на предыдущем шаге. Это также способствует уменьшению вычислительной сложности реализации способа, т.к. протяженность интервалов выбирают максимально возможной, а значит, и общее число выполнения аппроксимаций будет минимальным. Например, предположим, что исходная дискретная реализация содержит два участка, из которых один занимает 10% ее протяженности и имеет частотный спектр, верхняя граница которого в 10 раз превышает аналогичную границу на другом участке. Положим, что для хорошего восстановления тренда достаточно каждый из таких участков разбивать на 5 интервалов. Тогда, при применении описанного способа потребуется всего 5+5=10 интервалов разбиения исходной дискретной реализации. Если считать, что на адаптацию протяженности интервала потребуется повторять аппроксимацию, например, 5 раз на первом интервале и 5 раз при переходе на другой участок (число повторов равно отношению логарифма отношения максимальных частот на участке к логарифму коэффициентов k₁ или k₂), то общее число аппроксимаций окажется равным 20. Поскольку местонахождение участка с расширенным частотным спектром заранее неизвестно, то в способе прототипа временной отрезок разбивают на 50 интервалов, исходя из протяженности высокочастотного участка. Если при этом число повторных разбиений на участки, а значит, и повторных аппроксимаций задать равным 10 для получения приемлемого усреднения, то общее число аппроксимаций составит 500, то есть окажется в 25 раз больше, чем в предлагаемом способе.

Кроме того, информацию о тренде в предлагаемом способе можно хранить в виде набора значений коэффициентов на каждом из интервалов разбиения, что многократно меньше числа членов последовательности y_i на этих интервалах, тогда как в способе прототипа такой возможности нет.

Таким образом, использование предлагаемого способа выделения тренда нестационарного процесса с адаптацией интервалов аппроксимации приводит к уменьшению вычислительной сложности процесса выделения тренда.

Способ выделения тренда нестационарного процесса с адаптацией интервалов аппроксимации, заключающийся в том, что единственную дискретную реализацию нестационарного процесса, представляющую сумму полезного сигнала и шума, последовательно разбивают на интервалы, на каждом из которых осуществляют аппроксимацию методом наименьших квадратов, отличающийся тем, что ширину первого интервала выбирают равной части от общей продолжительности единственной дискретной реализации, выполняют аппроксимацию данного интервала и, если несоответствие аппроксимации превышает заданное значение, аппроксимацию повторяют, задавая ширину интервала равной части ее предыдущего значения, для каждого последующего интервала задают ширину, равную значению на предыдущем интервале, выполняют аппроксимацию и, если получают несоответствие аппроксимации меньше заданного значения установленное число раз подряд, то увеличивают ширину последующего интервала, а если получают несоответствие аппроксимации больше заданного значения, ширину текущего интервала выбирают равной части ее имеющегося значения и повторяют аппроксимацию, причем если ширина последнего интервала выходит за пределы единственной дискретной реализации нестационарного процесса, то ширину этого интервала ограничивают шириной оставшегося неаппроксимированного интервала.