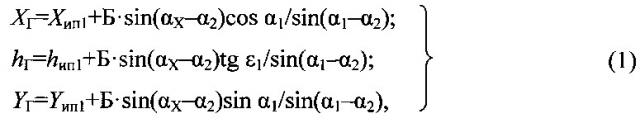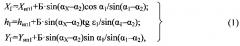Способ определения координат летательных аппаратов с использованием одного дирекционного угла и двух углов места

Способ определения координат летательных аппаратов с использованием одного дирекционного угла и двух углов места

Иллюстрации

Показать все

Реферат

Изобретение относится к области обнаружения и определения координат летательных аппаратов и может быть использовано в военной технике.

Известны различные способы определения координат объектов с использованием способов передачи и приема радиосигналов наземных радиомаяков (патент РФ №2436232) и способ триангуляции целей (патент РФ №2423720) [1, 2]. Недостатками данных способов является сложность обработки информации от пунктов обнаружения объектов, использование только активного радиолокационного диапазона электромагнитных волн.

Способ автоматизированного определения координат беспилотных летательных аппаратов (патент РФ №2523446 - прототип) [3], заключается в с применением камер кругового обзора, видеомонитора, ориентированного в пространстве, ЭВМ и лазерного дальномера для подсветки летательного аппарата, отличающийся тем, что камеры кругового обзора размещены симметрично и направлены в разные стороны, так чтобы вести наблюдение на 360° в оптическом диапазоне электромагнитных волн днем и ночью, и появление летательного аппарата фиксируется автоматически как помеха, возникающая на кадре видеопоследовательности относительно предыдущего, а полученные данные обрабатываются на ЭВМ, где вырабатываются угловые значения местонахождения летательного аппарата по высоте по горизонту относительно центра углоизмерительного устройства, которое с помощью поворотных механизмов направляет лазерный дальномер на летательный аппарат для измерения дальности до него, затем измеренная дальность от летательного аппарата поступает на устройство обработки и отображения информации (ЭВМ), где происходит автоматизирование определение пространственных координат X_БЛА, Y_БЛА, Z_БЛА летательного аппарата.

Основными недостатками являются демаскирующая составляющая данного способа, связанная с использования лазерного излучения, что снижает эффективность использования приведенного способа по обнаружению и определению пространственных координат летательных аппаратов в скрытом режиме работы, а также большие ошибки поворотных механизмов в процессе наведения лазерного дальномера и обработки полученной информации.

Как общий недостаток данных способов определения координат летательных аппаратов - не полное использование данных измерений и как следствие - не максимальная точность.

Задачей, стоящей перед настоящим изобретением, является повышение точности определения координат летательных аппаратов и уменьшения времени на обработку полученной информации в пассивном и активном режимах работы.

Поставленная задача решается следующим образом.

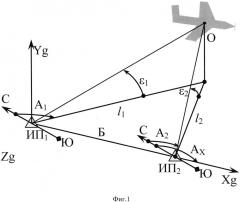
В настоящее время пеленгационный метод определения координат объектов широко распространен в практике оптических и радиолокационных внешнетраекторных измерений. Он основан на измерении угловых координат объекта в горизонтальной (азимут или дирекционный угол) и вертикальной (угол места) плоскостях (фиг. 1). В этом случае достаточно двух измерительных пунктов (ИП), чтобы однозначно определить пространственные координаты летательного аппарата.

В результате измерений с двух ИП определяются величины дирекционных углов и углов места (α₁; ε₁) и (α₂; ε₂), по которым пересчитываются координаты объекта в прямоугольной геодезической системе координат.

где Б - база, т.е. расстояние между ИП;

А_Х - азимут (дирекционный угол) с одного ИП на другой.

Дальнейшие обязательно синхронные измерения этих углов позволяет вычислять координаты объекта, относящиеся к последующим моментам времени.

Но уже в этом случае обращает на себя внимание тот факт, что в совокупности измеряемых параметров, которые составляет четверка чисел, содержится определенная избыточность данных, так как минимальная информация, необходимая для определения положения центра масс объекта (летательного аппарата) в любой СК, должна содержать три независимых измерения. Также об этом говорит то, что число степеней свободы материальной точки равно трем. Это обстоятельство подтверждается и видом указанных выше зависимостей, которые в качестве аргументов содержат лишь три величины (А₁, А₂, ε₁). Обычно четвертый параметр либо совсем отбрасывается, либо в лучшем случае используется для контроля. Однако и в том и другом случае информация теряется.

Из теории известно, что пара чисел (α; ε) геометрически однозначно определяет прямую в пространстве. При наличии двух измерительных пунктов таких прямых можно построить две. Данные прямые пересекаются в точке, где в момент засечки находится объект. Однако при наличии ошибок измерений прямые ИП_i-О в общем случае не пересекутся в одной точке, а будут являться скрещивающимися. Истинное положение объекта будет определяться некоторой областью пространства, которая будет тем больше, чем ниже точность измерений величин (A_i, ε_i). Повышения достоверности результатов можно добиться, увеличивая число ИП, но в этом случае использовать классические зависимости (1) не представляется возможным. Таким образом, необходимо искать иные пути обработки результатов ВТИ.

Минимальная информация, необходимая для определения положения центра масс объекта (летательного аппарата) в любой СК, должна содержать три независимых измерения.

В дальнейшем задача сводится к пересчету тройки исходных величин сферической СК в тройку искомых величин прямоугольной СК. Число возможных сочетаний троек чисел из четырех равно C³₄=4. Здесь возможны два принципиально разных геометрических подхода к решению задачи определения объекта.

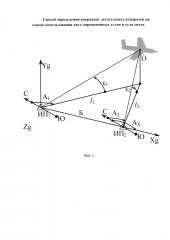
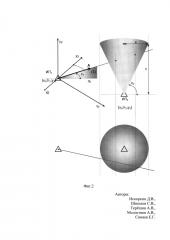
В качестве исходной информации служат величины (α₁; ε₁; ε₂) или (ε₁; α₂; ε₂). Первые две из них (α₁; ε₁) также определяют линию, проходящую через ИП₁ в направлении на объект. Геометрическим местом точек, для которых величина ε₂=const, есть прямой круглый конус с вертикальной осью симметрии и вершиной в ИП₂. Положение объекта в данном случае будет определяться точкой пересечения прямой и конуса (фиг. 2).

Плоскость и прямой круглый конус в пространстве могут располагаться одним из следующих образов (примем во внимание одну из двух частей конуса).

1. Прямая проходит через вершину конуса и совпадает с его образующей. В этом случае общих точек у этих объектов будет бесконечное множество.

2. Прямая проходит через вершину конуса и не совпадает с его образующей. В этом случае прямая и конус имеют одну общую точку - вершину.

3. Прямая параллельна образующей конуса, лежит вне его и не проходит через вершину. В этом случае общих точек у этих объектов нет.

4. Прямая параллельна образующей конуса, лежит внутри его и не проходит через вершину. В этом случае прямая и конус имеют одну общую точку.

5. Прямая не параллельна образующей конуса его и не проходит через вершину. В этом случае прямая и конус имеют либо две общие точки, либо таких точек нет.

Чаще всего на практике реализуется пятый случай. В том случае, когда точек пересечения две, необходимо вводить дополнительные условия выбора одной из них. В качестве такого может быть использовано условие близости к истинному решению, определенному хотя бы приближенно. В рассматриваемом случае в качестве истинного значения целесообразно использовать решение, полученное первым методом.

После получения четырех положений объекта за окончательное можно принять средневзвешенное значение, где в качестве веса целесообразно принять величины, обратные квадратам срединных ошибок измерений данных величин. Расчет их «вручную» невозможен, поэтому в первом приближении можно ограничиться среднеарифметическим из четырех значений.

Уравнение прямого круглого конуса с вертикальной осью симметрии, проходящей через ИП₂ (x₂; h₂; y₂), имеет вид

,

где а - радиус сечения конуса на высоте с от вершины.

Из фиг. 2 следует, что tg ε₂=с/а, тогда с=а tg ε₂. С учетом этого уравнение конуса перепишем в виде:

.

или

.

Уравнение прямой будет иметь вид

Подставляя величины х, h, y из параметрического уравнения прямой

x=x₁+kcosε₁cosα₁; h=h₁+ksinε₁; y=y₁+kcosε₁sinα₁

в уравнение конуса, получим

Раскладывая по степеням k, получим

или упрощая

;

;

.

Таким образом, получили квадратное уравнение относительно параметра k, решение которого имеет вид:

Д=b²-4ас; k_1,2=(-b±√Д)/2а.

Величина b четная, поэтому решение можно найти через ¹/₄Д.

Д/4=(b/2)²-ас; k₁,₂=[-(b/2)±√(¹/₄Д)]/а.

Определяют положение объекта в ГСК

x_Г=x₁+kcosε₁cosα₁; y_Г=y₁+ksinε₁cosα₁; y_Г=y₁+kcosε₁sinα₁.

Таким образом, способ определения пространственных координат летательных аппаратов на основе использования одного дирекционного угла и двух углов места, позволяющий определить положение летательного аппарата, в данном случае будет определяться точкой пересечения прямой и конуса, что уменьшает время обработки полученной информации от датчиков работающих в оптическом и радиолокационном диапазонах электромагнитных волн.

Источники информации

1. Панов В.П., Приходько В.В. Способ передачи и приема радиосигналов наземных радиомаяков. - ФИПС. Патент на изобретение №2436232, 10.12.2011 г.

2. Безяев B.C. Способ триангуляции целей. - ФИПС. Патент на изобретение №2423720, 10.07.2011 г.

3. Шишков С.В. Способ автоматизированного определения координат беспилотных летательных аппаратов. - ФИПС. Патент на изобретение №2523446, 26.05.2014 г.

Способ определения положения летательного аппарата в декартовой системе координат на основе засечки с двух измерительных пунктов с координатами

(х₁, h₁, у₁) и (х₂, h₂, у₂) одного дирекционного угла α₁ и двух углов места ε₁, ε₂ с последующей обработкой внешнетраекторной информации на ЭВМ путем решения геометрической задачи пересечения прямого круглого конуса с вертикальной осью симметрии и центром во втором измерительном пункте с прямой, проходящей через первый измерительный пункт, алгебраически сводящейся к поиску корней квадратного уравнения вида относительно параметра k вида

k²[cos²ε₁tg²ε₂-sin²ε₁]+k[2cos ε₁cos α₁(x₁-x₂)tg²ε₂+2cos ε₁sin α₁(y₁-y₂)tg²ε₂-

2sin ε₁(h₁-h₂)+(x₁-x₂)²tg²ε₂+(y₁-y₂)²tg²ε₂-(h₁-h₂)²=0,

и последующим определением искомых координат летательного аппарата (х_Г, h_Г, у_Г) по зависимостям вида: х_Г=x₁+k cosε₁cos α₁; h_Г=h₁+k sin ε₁; у_Г=y₁+k cos ε₁sin α_1.