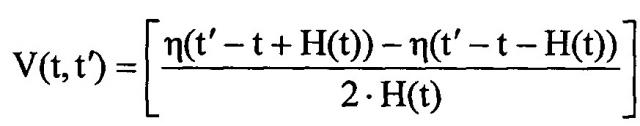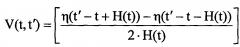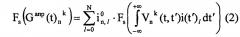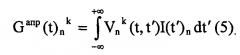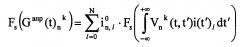Способ измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества (варианты)

Способ измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества (варианты)

Иллюстрации

Показать все

Реферат

Изобретение относится к области аналитических методов изотопной геохронологии и геохимии и предназначено для измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества, например, для измерения возрастного спектра при датировании образца ⁴⁰Аr/³⁹Аr методом.

В монографии [Dickin P. Radiogenic Isotope Geology. Cambridge Univ. Press, 2005. 506 p. (стр. 259-266)] (прототип) описана реализация при ⁴⁰Ar/³⁹Ar датировании, по всей видимости, единственного на сегодняшний день способа измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества, включающего следующие стадии: а) измерение количества каждого из изотопов в анализируемом веществе, выделенном из навески образца на каждом из этапов выделения анализируемого вещества из навески образца; б) введение в экспериментальные данные стандартных поправок; в) вычисление отношений ΔF/Δt, где F и t - количество первого и второго изотопа в анализируемом веществе, выделенном из навески образца, или иной непрерывный параметр, указывающий стадию выделения анализируемого вещества из навески образца, ΔF и Δt - приращения F и t, отвечающие этапу выделения анализируемого вещества из навески образца; и г) вычисление по полученным данным характеристики изотопной системы образца.

Конкретные реализации данного способа измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества (прототипа) могут отличаться анализируемым веществом [Farley K.А., Flowers R.M. (U-Th)/Ne and multidomain (U-Th)/He systematics of a hydrothermal hematite from eastern Grand Canyon // Earth and Planetary Science Letters. 2012. Vol. 359-360. P. 131-140.], способом выделения анализируемого вещества [Hyodo Н. Laser Probe ⁴⁰Ar/³⁹Ar Dating: History and Development from a Technical Perspective // Gondwana Research. 2008. Vol. 14. P. 609-616.], измеряемой характеристикой изотопной системы образца (например, возрастной спектр или изохронна) [Фор Г. Основы изотопной геологии. М.: Мир, 1989. 590 с. (стр. 108-118)] и т.д.

Основной недостаток известного способа измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества (прототипа) заключается в присутствии искажений характеристики изотопной системы образца, обусловленных усреднением истинных отношений ΔF/Δt при измерениях.

Имеет место следующее равенство:

где G(t) - измеряемая зависимость отношения ΔF/Δt от t; отношение ΔF/Δt, характеризующее определенный этап выделения анализируемого вещества из навески образца, отвечает интервалу по t, а не значению t, значения отношений ΔF/Δt поставлены в соответствие серединам интервалов по t, отвечающих данным отношениям ΔF/Δt,

- прямоугольное окно усреднения переменной ширины при усреднении истинных значений ΔF/Δt при измерениях,

H(t) - зависимость полуширины этапа выделения анализируемого вещества из навески образца по t от t; каждое значение полуширины этапа выделения анализируемого вещества из навески образца по t поставлено в соответствие середине интервала по t, отвечающего этому этапу выделения анализируемого вещества из навески образца,

η(t) - функция Хэвисайда,

I(t) - истинная зависимость отношения ΔF/Δt от t, то есть зависимость отношения ΔF/Δt, отвечающего бесконечно-малому интервалу по t вблизи значения t, от t.

Из равенства (1) видно, что измеряемая зависимость G(t) представляет собой истинную зависимость I(t) усредненную по t. Таким образом, в общем случае, измеряемая зависимость G(t) не совпадает с истинной зависимостью I(t), и, следовательно, на практике имеют место искажения характеристики изотопной системы образца, обусловленные усреднением истинных отношений ΔF/Δt при измерениях. При достаточно большой ширине прямоугольного окна усреднения V(t,t') и достаточно сложной зависимости H(t) (то есть зависимости полуширины прямоугольного окна усреднения V(t,t') от t), что не редко встречается на практике, отличия истинной зависимости I(t) от измеряемой зависимости G(t) могут быть весьма существенными, что, в свою очередь, может вызывать достаточно большие искажения характеристики изотопной системы образца.

Подавление искажений характеристики изотопной системы образца, обусловленных усреднением истинных отношений ΔF/Δt при измерениях, путем увеличения количества этапов выделения анализируемого вещества из навески образца во многих случаях затруднительно по ряду технических причин. Основная трудность заключается в отсутствии надежного контроля над количеством анализируемого вещества, выделяемого на каждом из этапов выделения анализируемого вещества из навески образца. Например, при ⁴⁰Аr/³⁹Аr датировании, параметром, фактически используемым для контроля над количеством анализируемого вещества, выделяемого на каждом из этапов выделения анализируемого вещества из навески образца, является температура. Если образец имеет узкий пик выделения анализируемого вещества по температуре (например, амфибол), то ширина одного из этапов выделения анализируемого вещества из навески образца по количеству аргона может быть очень велика (в некоторых случаях достигает 90% по доле выделенного ³⁹Аr). Кроме того, увеличение количества этапов выделения анализируемого вещества из навески образца будет приводить к уменьшению количества анализируемого вещества, выделяемого на каждом из этапов выделения анализируемого вещества из навески образца, что, в свою очередь, будет приводить к достаточно быстрому росту погрешности измерений. Увеличение средней массы навесок образцов крайне не желательно по ряду технических причин, например, из-за увеличения риска повреждения коллекторов масс-спектрометра, а также увеличения расходования ресурсов системы предварительной очистки газа.

Таким образом, основной недостаток известного способа измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества (прототипа) заключается в наличии искажений характеристики изотопной системы образца, обусловленных усреднением истинных отношений ΔF/Δt при измерениях.

Технический результат, на достижение которого направленно изобретение, заключается в подавлении искажений характеристики изотопной системы образца, обусловленных усреднением истинных отношений ΔF/Δt при измерениях.

Заявленный технический результат достигается следующим образом.

В способе измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества, включающем измерение количества каждого из изотопов в анализируемом веществе, выделенном из навески образца на каждом из этапов выделения анализируемого вещества из навески образца; введение в экспериментальные данные стандартных поправок; вычисление отношений ΔF/Δt; и вычисление по полученным данным характеристики изотопной системы образца выполняют следующие операции:

- осуществляют поэтапное выделение анализируемого вещества из навески образца для двух и более навесок одного и того же образца, устанавливая для разных навесок образца разные границы этапов выделения анализируемого вещества из навески образца по Т, за исключением нескольких границ этапов выделения анализируемого вещества из навески образца по Т, где Т - непрерывный параметр, указывающий стадию выделения анализируемого вещества из навески образца и изменяющийся для каждой из навесок образца в одинаковых пределах;

- формируют для каждой навески образца массивы данных М_m, представляющие зависимости F(t)_m, где индекс m указывает номера массивов данных М_m и зависимостей F(t)_m;

- множества точек, представляющие зависимости F(t)_m и заданные массивами данных М_m, разбивают на совокупности точек, представляющие участки зависимостей F(t)_m, и перемещают резко отклоняющиеся совокупности точек, представляющие участки зависимостей F(t)_m, вдоль координат F и t, сохраняя постоянными расстояния вдоль координат F и t между точками, принадлежащими одной и той же совокупности точек, представляющей участок зависимости F(t)_m, обеспечивая согласованность соответствующих друг другу зависимостей F(t)_m, полученных при выделении анализируемого вещества из различных навесок образца;

- растягивают (сжимают) зависимости F(t)_m вдоль координат F и t, обеспечивая совпадение точек соответствующих друг другу зависимостей F(t)_m, полученных при выделении анализируемого вещества из различных навесок образца, отвечающих одинаковым значениям Т;

По первому варианту,

- объединяют массивы данных М_m, представляющие соответствующие друг другу зависимости F(t)_m, полученные при выделении анализируемого вещества из различных навесок образца, в массивы данных D^*_n, представляющие соответствующие этим массивам данных зависимости F(t)^*_n, где индекс n указывает номера массивов данных D^*_n и зависимостей F(t)^*_n;

- аппроксимируют зависимости F(t)^*_n функциями F(t)^апр_n;

- вычисляют отношения ΔF/Δt как производные от соответствующих функций F(t)^апр_n;

По второму варианту:

- формируют по массивам данных М_m зависимости H(t)_n^k - зависимости полуширины этапа выделения анализируемого вещества из навески образца по t от t и соответствующие им зависимости G(t)_n^k - измеряемые зависимости отношения ΔF/Δt от t, где индекс n указывает номер множества В^*_n, В^*_n - непересекающиеся множества массивов данных М_m такие, что любая пара массивов данных М_m, принадлежащих одному и тому же множеству В^*_n, представляет пару соответствующих друг другу зависимостей F(t)_m, полученных при выделении анализируемого вещества из различных навесок образца, индекс к указывает номера зависимостей H(t)_n^k и G(t)_n^k;

- придавая индексу n различные значения и решая для каждого из этих значений следующую систему линейных алгебраических уравнений:

где F_s - линейный функционал, принадлежащий системе линейных функционалов F_s, индекс s указывает номер линейного функционала F_s,

G^апр(t)_n^k - функция, аппроксимирующая по крайней мере участок зависимости G(t)_n^k,

N - целое, неотрицательное число,

- функция, принадлежащая функциональному базису , индекс указывает номер функции

- коэффициент разложения функции I(t)_n в ряд Фурье по функциональному базису индекс n указывает номер функции I(t)_n, индекс указывает номер коэффициента

I(t)_n - функция, аппроксимирующая по крайней мере участок истинной зависимости отношения ΔF/Δt от t, индекс n указывает номер множества В^*_n которому соответствует данная истинная зависимость отношения ΔF/Δt от t,

где V_n^k(t,t') - прямоугольное окно усреднения переменной ширины при усреднении истинных значений ΔF/Δt при измерениях,

η(t) - функция Хэвисайда,

H^апр(t)_n^k - функция, аппроксимирующая по крайней мере участок зависимости H(t)_n^k, для каждого значения индекса n, индексы k и s принимают все возможные значения, вычисляют значения коэффициентов

- вычисляют функции I(t)_n по полученным значениям коэффициентов

- вычисляют отношения ΔF/Δt как значения функций I(t)_n.

В общем случае зависимости F(t)_m, соответствующие разным значениям индекса m, имеют разный физический смысл. Например, зависимость F(t)₁ может быть зависимостью количества ⁴⁰Аr, выделенного из первой навески образца, от количества ³⁹Аr, выделенного из первой навески образца; зависимость F(t)₂ может быть зависимостью количества ³⁶Аr, выделенного из первой навески образца, от количества ³⁹Аr, выделенного из первой навески образца; зависимость F(t)₃ может быть зависимостью количества ³⁹Аr, выделенного из второй навески образца при фиксированной температуре, от времени (например, при измерении диффузионной характеристики изотопной системы образца) и так далее. Под соответствующими друг другу зависимостями F(t)_m, полученными при выделении анализируемого вещества из различных навесок образца, понимают зависимости F(t)_m, имеющие одинаковый физический смысл, но полученные при выделении анализируемого вещества из различных навесок одного и того же образца.

В идеализированном случае, если навески образца содержат одинаковое количество анализируемого вещества, соответствующие друг другу зависимости F(t)_m, полученные при выделении анализируемого вещества из различных навесок образца, совпадают. Для ряда минералов данный факт подтверждают экспериментальные данные, полученные в ЦКП Многоэлементных и изотопных исследований СО РАН (Институт геологии и минералогии им. B.C. Соболева СО РАН, Новосибирск) (в частности см. пример 2).

На практике, выделение анализируемого вещества из различных навесок образца могут осуществлять в различных экспериментальных условиях. Например, навески образца могут отличаться содержанием анализируемого вещества из-за различия их масс; измерение количества каждого из изотопов в анализируемом веществе, выделенном из различных навесок образца, могут выполнять на разных масс-спектрометрах, требующих введения различных поправок, учитывающих разную чувствительность масс-спектрометра к разным изотопам анализируемого вещества (поправок на фракционирование) и т.д. Таким образом, в общем случае, соответствующие друг другу зависимости F(t)_m, полученные при выделении анализируемого вещества из различных навесок образца, согласованны друг с другом, то есть совпадают при надлежащем растяжении (сжатии) вдоль координат F и t; при этом надлежащий коэффициент растяжения (сжатия) зависимости F(t)_m вдоль координаты F может отличаться от надлежащего коэффициента растяжения (сжатия) той же зависимости F(t)_m вдоль координаты t.

На фиг. 1 схематически представлено множество точек, представляющее зависимость F(t)_m0 и заданное массивом данных М_m0; на фиг. 2 схематически представлено смещение совокупности точек, представляющей участок зависимости F(t)_m0, в результате действия случайных факторов; на фиг. 3 представлен возрастной спектр, полученный экспериментально при ⁴⁰Аr/³⁹Аr датировании образца пироксена, а также теоретическая модель истинного возрастного спектра того же образца пироксена; на фиг. 4 представлены зависимости F(t)₁ и F(t)₂, полученные при датировании долерита; на фиг. 5 представлены зависимости F(t)₁ и F(t)₂ после надлежащего растяжения (сжатия) вдоль координатных осей; на фиг. 6 показан поворот зависимостей F(t)₁ и F(t)₂ вокруг начала координат по направлению к оси t (после надлежащего растяжения (сжатия) вдоль координатных осей); на фиг 7 представлены полученные зависимости F(t)⁰₁ и F(t)⁰₂; на фиг 8 представлено разбиение множества точек, представляющего зависимость F(t)₂ и заданного массивом данных М₂, на две совокупности точек, представляющие участки зависимости F(t)₂; на фиг. 9 представлены зависимости F(t)⁰₁ и F(t)⁰₂ после перемещения второй совокупности точек, представляющей участок зависимости F(t)₂, вверх вдоль координаты F; на фиг. 10 представлены зависимости F(t)⁰₁ и F(t)⁰₂ после удаления одной точки зависимости F(t)₁ и одной точки зависимости F(t)₂; на фиг. 11 представлен возрастной спектр долерита полученный с помощью предложенного способа измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества; на фиг. 12 представлен возрастной спектр долерита полученный с помощью предложенного способа измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества, а также, возрастной спектр долерита полученный классическим способом по первой навески долерита; на фиг. 13 схематически представлено формирование зависимостей H(t)_n^k и G(t)_n^k.

Множество точек, представляющее зависимость F(t)_m0 и заданное массивом данных М_m0, где индекс m₀ - номер рассматриваемой зависимости F(t)_m, состоит из точек с координатами (t_p, F_p), где индекс р указывает порядковый номер точки с координатами (t_p, F_p). Если при этом на первом этапе выделения анализируемого вещества из навески образца F и t получают приращения Δ₁F и Δ₁t соответственно, на втором этапе выделения анализируемого вещества из навески образца F и t получают приращения Δ₂F и Δ₂t соответственно, и вообще, на этапе выделения анализируемого вещества из навески образца, имеющем порядковый номер q, F и t получают приращения Δ_qF и Δ_qt соответственно; то координаты (t_p, F_p) вычисляют следующим образом (фиг. 1):

Если на этапе выделения анализируемого вещества из навески образца, имеющем порядковый номер q₀, под действием каких-либо случайных причин приращение Δ_q0F и приращение Δ_q0t измерены некорректно, причем на всех остальных этапах выделения анализируемого вещества из навески образца приращения Δ_qF и Δ_qt измерены корректно; то все точки с координатами (t_p, F_p), начиная с точки с координатами (t_p, F_p), имеющей порядковый номер q₀, будут сдвинуты вдоль координаты F на некоторые одинаковые расстояния δ₁ и вдоль координаты t на некоторые одинаковые расстояния δ₂ (фиг. 2). Данное обстоятельство обусловлено тем, что координаты (t_p, F_p) определяют по формулам (3) и (4), то есть через суммы всех приращений Δ_qF и Δ_qt, предшествующих данной точке с координатами (t_p, F_p).

Чтобы исключить искажение координат (t_p, F_p), порядковые номера которых равны или следуют после q₀, множество точек, представляющее зависимость F(t)_m0 и заданное массивом данных М_m0, необходимо разбить на две совокупности точек, представляющие участки зависимости F(t)_m0: в первую совокупность точек, представляющую участок зависимости F(t)_m0, включить точки с координатами (t_p, F_p) порядковые номера которых предшествуют q₀, во вторую совокупность точек, представляющую участок зависимости F(t)_m0, включить точку с координатами (t_p, F_p) порядковый номер которой равен q₀, а также точки с координатами (t_p, F_p) порядковые номера которых следуют после q₀ (фиг. 2); и переместить вторую совокупность точек, представляющую участок зависимости F(t)_m0, вдоль координат F и t на расстояния δ₁ и δ₂ соответственно, сохраняя при этом постоянными расстояния вдоль координат F и t между точками с координатами (t_p, F_p), принадлежащими второй совокупности точек, представляющей участок зависимости F(t)_m0; то есть переместить так, чтобы зависимость F(t)_m0 стала такой, чтобы можно было добиться ее совпадения с соответствующими ей зависимостями F(t)_m, полученными при выделении анализируемого вещества из различных навесок образца, путем надлежащего растяжения (сжатия) вдоль координат F и t. Аналогичные выводы применимы и в случае, когда приращения Δ_qF и Δ_qt измерены некорректно не на одном этапе выделения анализируемого вещества из навески образца, а на нескольких этапах выделения анализируемого вещества из навески образца.

Таким образом, перемещение резко отклоняющихся совокупностей точек, представляющих участки зависимостей F(t)_m, вдоль координат F и t с сохранением постоянного расстояния вдоль координат F и t между точками, принадлежащими одной и той же совокупности точек, представляющей участок зависимости F(t)_m, позволяет добиться подавления влияния случайных факторов на точность измерения характеристики изотопной системы образца.

Растяжение (сжатие) зависимостей F(t)_m вдоль координат F и t, при котором совпадают точки соответствующих друг другу зависимостей F(t)_m, полученных при выделении анализируемого вещества из различных навесок образца, отвечающие одинаковым значениям Т - это растяжение (сжатие) зависимостей F(t)_m вдоль координат F и t при котором совпадают соответствующие друг другу зависимости F(t)_m, полученные при выделении анализируемого вещества из различных навесок образца. После растяжения (сжатия) зависимостей F(t)_m вдоль координат F и t, при котором совпадают соответствующие друг другу зависимости F(t)_m, полученные при выделении анализируемого вещества из различных навесок образца, массивы данных М_m, принадлежащие одному и тому же множеству В^*_n, представляют совпадающие зависимости, то есть одну и ту же функцию, и, следовательно, могут быть объединены в один массив данных D^*_n, представляющий соответствующую этому массиву данных зависимость F(t)^*_n. Зависимости F(t)^*_n, отвечающие различным значениям индекса n, имеют разный физический смысл. Иными словами, индекс n указывает физический смысл зависимости F(t)^*_n.

Для вычисления характеристики изотопной системы образца достаточно располагать множеством зависимостей F(t)^*_n. Количество экспериментальных точек, принадлежащих зависимостям F(t)^*_n, увеличивают путем увеличения количества навесок образца. Таким образом, путем увеличения количества навесок образца, обеспечивают достижение необходимой точности аппроксимации зависимостей F(t)^*_n.

Вычисление отношений ΔF/Δt как производных от соответствующих функций F(t)^апр_n, а также аппроксимация зависимостей F(t)^*_n с необходимой точностью за счет увеличения количества навесок образца, обеспечивают подавление искажений характеристики изотопной системы образца, обусловленных усреднением истинных отношений ΔF/Δt при измерениях.

Следует отметить два достаточно важных момента.

Если на одном из этапов выделения анализируемого вещества из навески образца под действием каких-либо случайных причин приращения ΔF и Δt, отвечающие одной из зависимостей F(t)_m, измерили некорректно, то вдоль координат F и t смещаются все последующие точки этой зависимости F(t)_m. Поскольку массивы данных D^*_n (представляющие зависимости F(t)^*_n) формируют путем объединения массивов данных М_m (представляющих зависимости F(t)_m) смещение вдоль координат F и t совокупностей точек, представляющих участки зависимостей F(t)_m, может приводить к существенному искажению достаточно больших участков зависимостей F(t)^*_n.

Таким образом, перемещение резко отклоняющихся совокупностей точек, представляющих участки зависимостей F(t)_m, вдоль координат F и t с сохранением постоянного расстояния вдоль координат F и t между точками, принадлежащими одной и той же совокупности точек, представляющей участок зависимости F(t)_m, значительно увеличивает точность аппроксимации зависимостей F(t)^*_n и, следовательно, значительно увеличивает точность измерения характеристики изотопной системы образца.

Все навески образца для удобства нумеруют натуральными числами 1, 2, 3 и т.д., то есть каждой навеске образца присваивают порядковый номер. При этом массив данных {D^*_n}₁ - это массив данных D^*_n, сформированный по экспериментальным данным, полученным при выделении анализируемого вещества из всех навесок образца порядковые номера которых меньше некоторого натурального числа N₁; массив данных {D^*_n}₂ - это массив данных D^*_n, сформированный по экспериментальным данным, полученным при выделении анализируемого вещества из всех навесок образца порядковые номера которых меньше некоторого натурального числа N₂, причем N₂>N₁; и вообще, массив данных {D^*_n}_j - это массив данных D^*_n, сформированный по экспериментальным данным, полученным при выделении анализируемого вещества из всех навесок образца порядковые номера которых меньше некоторого натурального числа N_j, индекс j принимает значения 1, 2, 3 и т.д., для любого значения индекса j выполняется неравенство N_j>N_j-1 (можно говорить о возрастающей последовательности натуральных чисел N_j). Таким образом, для каждого значения индекса n можно получить последовательность массивов данных {D^*_n}_j. С увеличением значения индекса j увеличивается количество навесок образца по которым формируют массив данных {D^*_n}_j.

По массиву данных {D^*_n}_j можно вычислить функцию {F(t)^апр_n}_j - функцию аппроксимирующая зависимость F(t), представленную массивом данных {D^*_n}_j (индексы n и j имеют тот же смысл, что и в обозначении массива данных {D^*_n}_j). Таким образом, для каждого значения индекса n можно получить последовательность функций {F(t)^апр_n}_j. С увеличением значения индекса j увеличивается количество навесок образца, при использовании которых вычисляют функцию {F(t)^апр_n}_j.

Массивы данных {D^*_n}_j формируют путем объединения массивов данных М_m, представляющих соответствующие друг другу зависимости F(t)_m, полученные при выделении анализируемого вещества из различных навесок образца. Поэтому если соответствующие друг другу зависимости F(t)_m, полученные при выделении анализируемого вещества из различных навесок образца, таковы, что можно добиться их совпадения друг с другом путем надлежащего растяжения (сжатия) вдоль координат F и t, а также перемещения резко отклоняющихся совокупностей точек, представляющих участки зависимостей F(t)_m, вдоль координат F и t с сохранением постоянного расстояния вдоль координат F и t между точками, принадлежащими одной и той же совокупности точек, представляющей участок зависимости F(t)_m; то увеличение количества используемых навесок образца (то есть увеличение значения индекса j) будет приводить лишь к уточнению функций {F(t)^апр_n}_j. В этом случае, последовательности функций {F(t)^апр_n}_j будут равномерно-сходящимися, то есть такими, что для любого значения t модуль разности {F(t)^апр_n}_j-{F(t)^апр_n}_j-1 может быть сделан сколь угодно малым за счет выбора достаточно большого значения индекса j. Последовательности функций {F(t)^апр_n}_j будут равномерно сходится к соответствующим истинным зависимостям F(t)^*_n.

Предложенный способ измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества применим когда последовательности функций {F(t)^апр_n}_j являются равномерно сходящимися. В противном случае, с увеличением значения индекса j функции {F(t)^апр_n}_j будут только усложняться, не стремясь равномерно к некоторой предельной функции (истинной зависимости F(t)^*_n), то есть последовательности функций {F(t)^апр_n}_j не будут равномерно сходящимися.

Таким образом, предложенный способ измерения характеристики изотопной системы образца при поэтапном выделении анализируемого вещества позволяет выполнять проверку его применимости, без привлечения других, независимых, способов измерения характеристики изотопной системы образа при поэтапном выделении анализируемого вещества.

По второму варианту по массивам данных М_m формируют зависимости H(t)_n^k и соответствующие им зависимости G(t)_n^k.

Из равенства (1) следует что:

Замена в данном интегральном уравнении (интегральное уравнение Фредгольма первого рода) функции I(t)_n на сумму первых (N+1) членов разложения функции I(t)_n в ряд Фурье по функциональному базису [Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа. 2000. 462 с. (стр. 29-33); Лебедев В.И. Функциональный анализ и вычислительная математика. М.: Всероссийский институт научной и технической информации. 1994. 212 с. (стр. 62-63)]; действие на обе части полученного равенства линейным функционалом F_s [Вулих Б.З. Введение в функциональный анализ. М., Государственное издательство физико-математической литературы, 1958, 352 с. (стр. 29-30)]; а также изменение значений индексов s и k; для каждого значения индекса n дают систему линейных алгебраических уравнений (2). Каждому множеству В^*_n, отвечает единственная истинная зависимость отношения ΔF/Δt от t; одной и той же истинной зависимости отношения ΔF/Δt от t в общем случае отвечает несколько пар зависимостей H(t)_n^k и G(t)_n^k. Поэтому каждому значению индекса n отвечает своя система линейных алгебраических уравнений (2); линейные алгебраические уравнения, входящие в одну и ту же систему линейных алгебраических уравнений (2), в общем случае отличаются не только значениями индексов s но и значениями индексов k.

Решение системы линейных алгебраических уравнений (2) позволяет вычислить коэффициенты то есть коэффициенты разложения функции I(t)_n в ряд Фурье по функциональному базису . Суммирование ряда Фурье, представляющего функцию I(t)_n, позволяет вычислить функцию I(t)_n и, следовательно, отношения ΔF/Δt.

Если количество базисных линейных алгебраических уравнений, входящих в систему линейных алгебраических уравнений (2), больше количества коэффициентов , то система линейных алгебраических уравнений (2) может быть решена методом наименьших квадратов [Вержбицкий В.М. Основы численных методов. М.: Высшая школа. 2002. 848 с. (стр. 404-408); Шевцов Г.С. Линейная алгебра. М.: МАГИСТР ИНФРА-М. 2011. 525 с. (стр. 357-378)]. В этом случае, чем больше линейно независимых линейных алгебраических уравнений будет входить в систему линейных алгебраических уравнений (2), тем точнее будет вычислена функция I(t)_n и, следовательно, отношения ΔF/Δt. Количество линейно независимых линейных алгебраических уравнений, входящих в систему линейных алгебраических уравнений (2), увеличивают путем увеличения количества зависимостей H(t)_n^k и G(t)_n^k, а также за счет выбора различных видов зависимостей H(t)_n^k. При необходимости увеличивают количество навесок образца.

Таким образом, с физической точки зрения, по второму варианту, накопление необходимых экспериментальных данных обеспечивают не только за счет увеличения количества навесок образца, но и за счет изменения вида зависимостей полуширины этапа выделения анализируемого вещества из навески образца по t от t при измерениях.

Интегральное уравнение (5) может быть сведено к системе линейных алгебраических уравнений непосредственно - путем замены интеграла квадратурной суммой и изменением значений t [Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: БИНОМ. Лаборатория знаний. 2008. 636 с. (стр. 602-603); Вержбицкий В.М. Основы численных методов. М.: Высшая школа. 2002. 848 с. (стр. 663-668)]. Из-за того, что ядро интегрального уравнения (5) представляет собой прямоугольное окно усреднения переменной ширины, матрица получаемой системы линейных алгебраических уравнений будет иметь ленточную структуру, причем ненулевая часть каждой строки этой матрицы будет состоять из одинаковых элементов. В результате этого большинство линейных алгебраических уравнений, входящих в полученную систему линейных алгебраических уравнений, будут линейно зависимы (причем, строго линейно зависимы). Описанный выше способ сведения интегрального уравнения (5) к системе линейных алгебраических уравнений (2), основанный на переходе от функции I(t)_n к ее разложению в ряд Фурье по функциональному базису и действии на обе части полученного равенства линейным функционалом F_s, позволяет получить существенно большее количество линейно независимых линейных алгебраических уравнений. Данное обстоятельство позволяет снизить количество навесок образца, необходимых для получения достаточного количества линейно независимых линейных алгебраических уравнений, необходимых для надежного вычисления функции I(t)_n.

Если система линейных алгебраических уравнений (2) плохо обусловлена [Вержбицкий В.М. Основы численных методов. М.: Высшая школа. 2002. 848 с. (стр. 28-32)], то для ее решения используют один из существующих методов регуляризации [Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: БИНОМ. Лаборатория знаний. 2008. 636 с. (стр. 304-309); Шевцов Г.С. Линейная алгебра. М.: МАГИСТР ИНФРА-М. 2011. 525 с. (стр. 378-381)].

При вычислении отношений ΔF/Δt путем решения системы линейных алгебраических уравнений (2) погрешность вычисления характеристики изотопной системы образца, в некоторых случаях, может быть ниже, чем при вычислении отношений ΔF/Δt как производных от функций F(t)^апр_n. Данный факт обусловлен следующим обстоятельством. При вычислении отношений ΔF/Δt путем решения системы линейных алгебраических уравнений (2), значения данных отношений вычисляют по зависимостям G(t)_n^k и H(t)_n^k, то есть по измеряемым значениям отношений ΔF/Δt и значениям полуширин этапов выделения анализируемого вещества из навески образца по t. Изотопные отношения, как правило, измеряют точнее, чем количество того или иного изотопа в анализируемом веществе.

Пример 1 (искажение характеристики изотопной системы образца при измерении известным способом).

На примере ⁴⁰Аr/³⁹Аr датирования образца пироксена (автор образца Афанасьев В.П.), проведенного в ЦКП Многоэлементных и изотопных исследований СО РАН (Институт геологии и минералогии им. B.C. Соболева СО РАН, Новосибирск), показано на сколько могут быть велики искажения характеристики изотопной системы образца, обусловленные усреднением истинных отношений ΔF/Δt при измерениях (фиг. 3).

Возрастной спектр, полученный экспериментально при ⁴⁰Аr/³⁹Аr датировании образца пироксена, обозначен сплошной линией. Усреднение изотопных отношений ⁴⁰Аr/³⁹Аr по доле выделенного ³⁹Аr, имевшее место при измерении возрастного спектра, полученного экспериментально при ⁴⁰Аr/³⁹Аr датировании образца пироксена, преобразует возрастной спектр, обозначенный пунктирной линией, в возрастной спектр, совпадающий в приделах погрешности с возрастным спектром, полученным экспериментально при ⁴⁰Аr/³⁹Аr датировании образца пироксена. Следовательно, возрастной спектр, обозначенный пунктирной линией, представляет собой теоретическую модель истинного возрастного спектра образца пироксена. Сравнение данных возрастных спектров (фиг. 3) показывает, что искажения характеристики изотопной системы образца, обусловленные усреднением истинных отношений ΔF/Δt при измерениях, могут быть весьма существенны, в данном примере искажения по возрасту порядка 90 млн лет, то есть примерно в 5 раз больше расчетной погрешности.

Приведенный пример является далеко не единственным, например, аналогичные возрастные спектры можно найти в работах [Vincenzo G.D., Rocchi S., Rossetti F., Storti F. 40Ar/39Ar dating of pseudotachylytes: the effect of clast-hosted extraneous argon in Cenozoic fault-generated friction melts from the West Antarctic Rift System // Earth and Planetary Science Letters, 2004, v. 223, p. 349-364.; Negro F., Sigoyer J., Goffe В., Saddiqi O., Villa I.M. Tectonic evolution of the Betic-Rif arc: New constraints from 40Ar/39Ar dating on white micas in the Temsamane units (External Rif, northern Morocco) // Lithos, 2008, v. 106, p. 93-109.; Gibsher A.A., Malkovets V.G., Travin A.V., Belousova E.A., Sharygin V.V., Konc Z. The age of camptonite dikes of the Agardag alkali-basalt complex (western Sangilen): results of 40Ar/39Ar and U/Pb dating // Russian Geology and Geophysics, 201