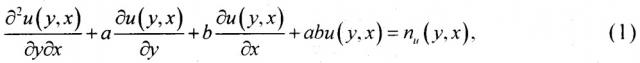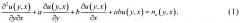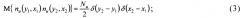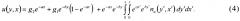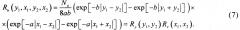Способ моделирования изображений в радиолокационных системах дистанционного зондирования протяженных объектов

Способ моделирования изображений в радиолокационных системах дистанционного зондирования протяженных объектов

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиотехники и может быть использовано в радиолокационных системах дистанционного зондирования протяженных объектов.

Известен способ восстановления (формирования) изображений в радиолокационных системах дистанционного зондирования протяженных объектов (автоматизированных системах радиовидения), который предполагает получение оценки поля изображения в виде выходного сигнала согласованного фильтра [1. Кондратенков Г.С. Радиовидение. Радиолокационные системы дистанционного зондирования Земли: учебное пособие для вузов / Г.С. Кондратенков, А.Ю. Фролов; под ред. Г.С. Кондратенкова. - М: Радиотехника, 2005. - с. 135-159]. Необходимо отметить, что в данной постановке понятия «восстановление» и «формирование» изображений совпадают.

Недостатком известного способа является то, что процедура согласованной фильтрации принадлежит к классу некорректно поставленных задач [2, 3], т.е. бесконечно малым приращениям входного воздействия (траекторного сигнала) могут соответствовать бесконечно большие приращения результата восстановления. Помимо наличия систематической и флуктуационной ошибок, это приводит к неустойчивости решения задачи восстановления изображений. Так, например, даже при больших отношениях сигнал/шум решение может быть неустойчивым из-за наличия нулей в спектре функции неопределенности, лежащих в пределах полосы пространственных частот изображения [4]. Следовательно, возникает необходимость регуляризации решения - существенного уменьшения разброса решений относительно истинного значения.

В сложившихся условиях альтернативой является способ восстановления изображений в радиолокационных системах дистанционного зондирования протяженных объектов, основанный на байесовском подходе, где в качестве параметра регуляризации решения используется априорная корреляционная функция модели восстанавливаемого изображения [5. Коренной А.В. Оптимальное восстановление изображений в радиолокационных системах мониторинга земной поверхности / А.В. Коренной, С.А. Лепешкин // Успехи современной радиоэлектроники. - 2010. - №11. - С. 6-9].

Целью заявляемого изобретения является обоснование адекватности и выбор параметров математических моделей восстанавливаемых изображений в радиолокационных системах дистанционного зондирования протяженных объектов.

Сущность изобретения состоит в следующем. Исходя из физических соображений плоское изображение можно представить в виде поля значений яркости. Такое поле можно задать функцией трех переменных u(t, y, x), где t - время; y, x - пространственные координаты. Значения функции u определяют меняющуюся во времени яркость изображения в каждой точке пространства [6].

Для описания математической модели поля изображения u(t, y, x) целесообразно воспользоваться аппаратом стохастических дифференциальных уравнений в частных производных, который непосредственно указывает способ генерации реализаций поля, а также позволяет производить анализ вероятностных характеристик получаемых моделей. Исходя из этого имеет смысл ограничиться хорошо изученными уравнениями математической физики [7, 8]. Известно, что к основным уравнениям математической физики относятся три типа линейных дифференциальных уравнений в частных производных второго порядка: гиперболические, параболические, эллиптические. Исходя из физических соображений будем полагать, что за время работы системы радиовидения формируемое радиолокационное изображение (РЛИ) будет статическим, так как время синтезирования не превышает десятка секунд, т.е. для РЛИ зависимость функции и от времени t будет отсутствовать.

Гиперболическое уравнение. В [9] для описания моделей двумерных случайных полей предлагается использовать дифференциальные уравнения в частных производных гиперболического типа. Рассмотрим, как один из вариантов этих моделей, краевую задачу вида

u(0, x)=g₁, u(y, 0)=g₂,

где а>0, b>0; g₁, g₂ = const.

Здесь n_u(y, x) - белое гауссовское шумовое поле с известными характеристиками

где М {⋅} - операция математического ожидания.

Для решения уравнения (1) применен метод замены переменных [9]. В результате решение краевой задачи (1) будет иметь вид

На фиг. 1 приведены полутоновые изображения реализаций гиперболической модели размером 50×50 элементов, полученных в результате моделирования на ЭВМ выражения (4) для различных значений параметров a и b.

Поскольку входное воздействие n_u(y, x) является гауссовым, а уравнение (1) - линейным, то и поле u(y, x) также будет гауссовым. Следовательно, исчерпывающими статистическими характеристиками u(y, x) являются математическое ожидание и корреляционная функция.

С учетом (2) и (4) определим математическое ожидание поля u(y, x):

Тогда корреляционная функция модели изображения будет определяться как

Подставив (4) в (6) и выполнив операцию усреднения, получим

Из (7) видно, что корреляционная функция R_u(y₁, x₁, y₂, x₂) факторизуется и может быть представлена в виде произведения двух корреляционных функций по различным координатам, т.е. для данной модели значения поля по координатам y и x независимы. Кроме того, выражение (7) свидетельствует о наличии причинных связей между значениями поля по обеим координатам, так как корреляционная функция убывает с увеличением расстояния между значениями поля по каждой координате.

Таким образом, гиперболическое уравнение относится к классу каузальных моделей.

Для наглядного сравнения статистических характеристик различных моделей приведем их корреляционные функции к удобному для визуального восприятия двумерному виду путем усреднения по пространственным координатам y₂ и x₂. На фиг. 2 приведены графики усредненной корреляционной функции гиперболической модели, полученные на основе решения уравнения (7) для соответствующих значений параметров a и b.

Параболическое уравнение. Рассмотрим одну из краевых задач для уравнения параболического типа

u(0, x)=g₁, u(y, 0)=g₂, u(y, L_c)=g₃,

где a>0, b>0, L_c - длина строки изображения.

Применив метод функций Грина [10], получили решение краевой задачи (8), которое определяться выражением

где .

На фиг. 3 приведены полутоновые изображения реализаций параболической модели размером 50×50 элементов, полученные в результате моделирования на ЭВМ выражения (9) для различных значений параметров a и b.

Определяя статистические характеристики, получим, что математическое ожидание поля равно сумме второго и третьего членов в правой части (9), а корреляционная функция будет иметь вид

Из анализа (10) можно сделать вывод об отсутствии у параболических моделей причинных связей между значениями поля изображения по координате x, так как степень корреляционной зависимости значений поля определяется не столько расстоянием между этими значениями по координате x, сколько их взаимным расположением на этой координате. Следовательно, параболические уравнения относятся к классу полукаузальных моделей.

На фиг. 4 приведены двумерные графики усредненной по пространственным координатам y₂ и x₂ корреляционной функции параболической модели, полученные на основе решения уравнения (10) для соответствующих значений параметров a и b.

Эллиптическое уравнение. Из широкого круга краевых задач для эллиптических уравнений рассмотрим краевую задачу, которая по своей физической сути может быть использована для описания плоских изображений

u(0, x)=g₁, u(y, 0)=g₂, u(L_k, x)=g₃, u(y, L_с)=g₄,

где L_с и L_k - длина строки и длина кадра изображения соответственно.

Краевая задача (11) решена методом Фурье. В результате получено

где .

На фиг. 5 приведены полутоновые изображения реализаций эллиптической модели размером 50×50 элементов, полученные в результате моделирования на ЭВМ выражения (12) для различных значений параметра a.

Определяя по аналогии с предыдущими случаями корреляционную функцию эллиптической модели, получим

Как видно из (13), эллиптические модели являются некаузальными по обеим координатам. Для полей, описываемых такими моделями, характерным является то, что наиболее коррелированными являются те значения поля, которые расположены ближе к центру плоскости xy.

На фиг. 6 приведены двумерные графики усредненной по пространственным координатам y₂ и x₂ корреляционной функции эллиптической модели, полученные на основе решения уравнения (13) для соответствующих значений параметра а

Понятие каузальности тесно связано с типом изображения. Так для каузальных изображений наличие причинно-следственных связей во всех направлениях обеспечивает однородность всего изображения, т.е. отсутствие особенностей в каком-либо направлении. К таким изображениям можно отнести, например, РЛИ лесного массива, сельскохозяйственных угодий, морской поверхности и др. Отсутствие каузальности приводит к возникновению неоднородностей (особенностей) в изображении на каких-либо участках. Изображениями некаузального типа будут являться, например, РЛИ одиночных и групповых объектов, РЛИ крупномасштабных объектов на различных фонах (здания, сооружения, корабли на рейде, самолеты на аэродроме и т.д.), РЛИ воздушных и космических объектов, полученные системами радиовидения с обратным синтезированием апертуры антенны и т.п.

Как видно из фиг. 1, 3, 5, при определенных значениях параметров a и b реализации моделей визуально соответствуют РЛИ с высокой (фиг. 1б, 5б) или низкой (фиг. 3б) пространственной динамикой яркости, причем соответствующие им корреляционные функции (фиг. 2б, 4б, 6б) также приобретают характерный, отличный от других, внешний вид, что подтверждает гипотезу о возможности осуществления на их основе регуляризации решения в процессе оптимальной обработки изображений в автоматизированных системах радиовидения.

Таким образом, установлено, что с помощью трех типов моделей можно описать различные по характеру РЛИ, а также, выявлена связь между типом РЛИ и статистическими характеристиками модели.

Для того чтобы оценить степень адекватности математической модели реальному РЛИ, необходимо сравнить соответствующие вероятностные характеристики модели и статистические характеристики реальных РЛИ. Исчерпывающей вероятностной характеристикой модели является ее корреляционная функция R_u, которая играет роль параметра регуляризации при использовании байесовского метода восстановления изображений [5]. Соответствующей статистической характеристикой реальных РЛИ является статистическая корреляционная функция R₀. Аппроксимировав статистическую корреляционную функцию R₀ подходящим аналитическим выражением для R_u, можно говорить об адекватности математической модели реальному РЛИ. Подобные задачи аппроксимации решаются, например, методом наименьших квадратов из условия минимума среднего квадрата ошибки (СКО) ε для различных значений параметров моделей a и b, т.е.

Если корреляционные функции R_u(y₁, x₁, y₂, x₂) трех типов моделей имеют аналитические выражения (7), (10) и (13) соответственно, то корреляционные функции реальных РЛИ R₀(y₁, x₁, y₂, x₂) можно получить только с помощью статистической обработки экспериментальных данных.

В качестве статистической характеристики РЛИ использовано следующее определение пространственной корреляционной функции

где , .

Здесь u_n(y, x) - нормированное значение «яркости» n-го РЛИ из выборки размера N изображений определенного типа; м{u_n(y, x)} - операция усреднения по всему множеству N изображений определенного типа, используемых при статистической обработке.

Возможность такой интерпретации статистической пространственной корреляционной функции (15) была доказана путем машинного моделирования. На основе критерия (14) проведено сравнение корреляционной функции R_u параболической модели (10) и корреляционной функции R₀, полученой статистически из выражения (15) на основе N реализаций параболической модели (9) при одних и тех же значениях параметров а и b.

Результаты сравнения вероятностных характеристик приведены на фиг. 7. Из графика видно (фиг. 7), что при статистической выборке N≥1000, значение СКО между пространственными корреляционными функциями модели РЛИ, полученными аналитически и статистически при прочих равных условиях, не превышает 2%. Следовательно, использование выражения (15) для расчета статистической корреляционной функции реальных РЛИ определенного типа возможно, при количестве испытаний N≥1000 [11]. Графики усредненной статистической корреляционной функции параболической модели, рассчитанные для различного числа испытаний N (фиг. 8), подтверждают вышеизложенный вывод.

Для осуществления выбора параметров моделей РЛИ, соответствующих реальным РЛИ определенного типа, необходимо подобрать N≥1000 различных изображений со сходной пространственной динамикой яркости, что не всегда представляется возможным. Эту проблему предлагается решить путем подготовки множества исходных РЛИ с помощью «вырезания» случайных тестовых участков РЛИ меньшего размера из одного большого типового РЛИ, основываясь на свойстве его эргодичности по пространству (для систем дистанционного зондирования земной поверхности), или же за счет имитации изменения ракурса наблюдения путем вращения тестового РЛИ вокруг своей оси (для систем формирования крупномасштабных РЛИ воздушных и космических объектов).

Методика подготовки исходного материала для расчета вероятностных характеристик реальных РЛИ определенного типа представлена на фиг. 9 и 10.

Таким образом, предлагается способ моделирования изображений в радиолокационных системах дистанционного зондирования протяженных объектов в виде алгоритма выбора модели РЛИ и ее наилучших пареметров для реальных РЛИ определенного типа, проводимого на основе сравнения соответствующих вероятностных характеристик моделей: гиперболической (7), параболической (10) и эллиптической (13), и статистических характеристик реальных РЛИ (15), из условия минимума СКО для различных значений параметров моделей a и b (14).

Структурная схема алгоритма, реализующего разработанный способ, представлена на фиг. 11.

Расчет происходит параллельно в модулях гиперболической, параболической и эллиптической моделей. Например, в модуле гиперболической модели: в блоке 1 формируется матрица параметров a и b с необходимым шагом дискретизации; в блоке 2 для каждого значения a_i и b_j вычисляется аналитическая корреляционная функция модели R_uij (7); в блоке 4 на основе метода наименьших квадратов осуществляется сравнение корреляционных функций - статистической R₀, полученой в блоке 3 для N≥1000 реальных РЛИ определенного типа (15), и аналитической R_uij, поступающей из блока 2, - путем расчета СКО ε_ij (14); в блоке 5 определяется наименьшее значение СКО для гиперболической модели и вместе с соответствующими значениями поступает в блок 6. В блоке 6 осуществляется сравнение минимальных значений СКО, полученных в каждом из модулей для соответствующих моделей, и на выход выдается результат в виде корреляционной функции модели РЛИ R_oпт, наиболее соответствующей заданному типу РЛИ [11].

Очевидно, что предлагаемый способ может быть использован как для предварительной настройки системы восстановления РЛИ определенного типа, так и для адаптации системы обработки РЛИ к изображениям определенного типа путем подстройки параметров соответствующей модели РЛИ в процессе восстановления изображений.

Результаты машинного моделирования алгоритма выбора модели РЛИ и ее наилучших параметров для реальных РЛИ определенного типа, реализующего разработанный способ, представлены в таблице 1. А в качестве примера на фиг. 12 и 13 приведены графики усредненных корреляционных функций реальных изображений и соответствующих моделей при наилучших значениях параметров.

Анализируя минимальные значения СКО для различных моделей (таблица 1), можно сделать вывод, что каузальная и полукаузальная модели достаточно хорошо описывают РЛИ участка земной поверхности, а некаузальная модель - РЛИ крупномасштабных объектов.

Таким образом, математические модели РЛИ в виде случайных полей на основе стохастических дифференциальных уравнений в частных производных трех типов: гиперболического, параболического и эллиптического, позволяют получить аналитическое выражение для параметра регуляризации - априорной корреляционной функции модели изображения - при решении некорректной задачи восстановления изображений в системах радиовидения с использованием метода оптимальной обработки случайных полей, основанного на байесовском подходе.

Новизна изобретения заключается в новом подходе к процессу моделирования изображений в радиолокационных системах дистанционного зондирования протяженных объектов, основанном на применении в качестве моделей восстанавливаемого изображения - стохастических дифференциальных уравнений в частных производных второго порядка с соответствующими вероятностными характеристиками.

Изобретательский уровень характеризуется применением известного ранее научно-методического аппарата стохастических дифференциальных уравнений в частных производных второго порядка для решения задачи моделирования изображений в радиолокационных системах дистанционного зондирования протяженных объектов.

Данное изобретение является промышленно применимым при разработке перспективных и модернизации существующих радиолокационных систем дистанционного зондирования протяженных объектов.

Источники информации

1. Кондратенков Г.С. Радиовидение. Радиолокационные системы дистанционного зондирования Земли: учебное пособие для вузов / Г.С. Кондратенков, А.Ю. Фролов; под ред. Г.С. Кондратенкова. - М.: Радиотехника, 2005. - 368 с.

2. Тихонов А.Н. Методы решения некорректных задач: учебное пособие для вузов / А.Н. Тихонов, В.Я. Арсенин; изд. 3-е, исправленное. - М.: Наука, 1986. - 288 с.

3. Василенко Г.И. Восстановление изображений / Г.И. Василенко, A.M. Тараторин. - М.: Радио и связь, 1986. - 304 с.

4. Фалькович С.Е. Оптимальный прием пространственно-временных сигналов в радиоканалах с рассеянием / С.Е. Фалькович, В.И. Пономарев, Ю.В. Шкварко. - М.: Радио и связь, 1989. - 296 с.

5. Коренной А.В. Оптимальное восстановление изображений в радиолокационных системах мониторинга земной поверхности / А.В. Коренной, С.А. Лепешкин // Успехи современной радиоэлектроники. - 2010. - №11. - С. 6-9.

6. Коренной А.В. Математические модели полутоновых изображений // Радиотехника. - 2007. - №8. - С. 79-81.

7. Тихонов А.Н. Уравнения математической физики / А.Н. Тихонов, А.А. Самарский. - М.: Издательство МГУ, 1999. - 799 с.

8. Котляков Н.С. Уравнения в частных производных математической физики / Н.С. Кошляков, Э.Б. Глинер, М.М. Смирнов. - М.: Высшая школа, 1970. - 712 с.

9. Ярлыков М.С. Математические модели гауссовских случайных полей в виде стохастических дифференциальных уравнений в частных производных / М.С. Ярлыков, Ю.Н. Моисеенко // Авиационные радиоэлектронные комплексы и их эксплуатация. Научно-методические материалы. - М.: ВВИА, 1988. - С. 27-39.

10. Бутковский А.Г. Характеристики систем с распределенными параметрами / А.Г. Бутковский. - М.: Наука, 1979. - 114 с.

11. Коренной А.В. Моделирование радиолокационных изображений на основе стохастических дифференциальных уравнений в частных производных / А.В. Коренной, С.А. Лепешкин, А.П. Кадочников, Е.А. Ященко // Радиотехника. - 2016. - №10. - С. 134-144.

Способ моделирования изображений в радиолокационных системах дистанционного зондирования протяженных объектов, заключающийся в разработке моделей восстанавливаемого (формируемого) изображения, отличающийся тем, что в качестве математической модели восстанавливаемого радиолокационного изображения используют стохастические дифференциальные уравнения в частных производных второго порядка, которые позволяют описать различные по характеру изображения, то есть непосредственно указывают способ генерации реализаций модели изображения, а также определить связь между типом изображения и вероятностными характеристиками моделей за счет аппроксимации статистической корреляционной функции реальных изображений определенного типа подходящим аналитическим выражением для корреляционных функций разработанных моделей, причем полученную априорную корреляционную функцию модели используют в дальнейшем в качестве параметра регуляризации при решении задачи оптимального восстановления изображений в радиолокационных системах дистанционного зондирования протяженных объектов.