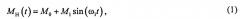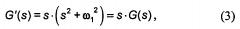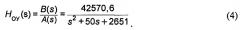Способ устранения влияния гармонических возмущений момента нагрузки в электромеханической системе

Способ устранения влияния гармонических возмущений момента нагрузки в электромеханической системе

Иллюстрации

Показать все

Реферат

Изобретение относится к разделу управления и может быть использовано при регулировании параметров сложных электромеханических систем, например электроприводов постоянного и переменного тока.

Существует ряд технических объектов, приводимых в движение средствами автоматизированного электропривода, наличие дефектов в изготовлении механической части которых (например, эксцентриситета валов рабочих органов и систем передач движения) приводит к возникновению гармонических колебаний статического момента нагрузки на валу рабочих органов. При этом частота таких колебаний жестко связана со скоростью электродвигателя, когда момент нагрузки на валу рабочего органа М_Н(t) можно представить в виде:

где М₀ - постоянная составляющая момента; M₁ - амплитуда колебаний момента; ω₁ - скорость рабочего органа; t - время.

Для возмущающего воздействия (1), состоящего из постоянной и гармонической составляющих, соответствующее изображение Лапласа имеет вид

где s - комплексная переменная Лапласа; ; Ω - частота вращения электродвигателя; i - передаточное отношение редуктора.

Минимизация последствий подобных возмущений позволяет значительно улучшить показатели качества систем автоматического управления скоростными режимами технологических установок. Снижение флуктуаций момента нагрузки и, как следствие, скорости рабочих органов технологических машин оказывает существенное влияние на качество выпускаемой продукции. При этом увеличивается точность изготовления деталей при металлообработке, стабилизируются геометрические размеры длинномерных материалов при обработке изделий в поточных линиях (диаметр волокна или провода, толщина пленки и различных покрытий), нормируются их весовые показатели (плотность бумаги, ткани и др.), улучшается светопропускание оптических световодов и т.п.

Известен «Способ каскадного автоматического регулирования» (источник патент РФ №2127895, МПК6 G05B 13/02, год опубликования 1999), заключающийся в том, что осуществляют измерение вспомогательного параметра объекта и стабилизацию его с помощью одноконтурной системы регулирования, измерение основного параметра объекта, стабилизации его с помощью астатической одноконтурной системы регулирования и формирования сигнала задания регулятору внутреннего контура, при этом устанавливают сигналы задания верхнего и нижнего допустимых значений вспомогательного параметра объекта для регулятора внутреннего контура и определяют на заданном интервале ошибку рассогласования для астатического регулятора внешнего контура, воздействующего посредством исполнительного устройства на объект в заданном интервале с помощью аналогового сигнала, определяемого законом регулирования астатического регулятора внешнего контура, при выходе вспомогательного параметра объекта из заданного интервала с выхода регулятора внутреннего контура на исполнительное устройство подают управляющее воздействие релейного типа со знаком, уменьшающим отклонение вспомогательного параметра объекта от верхнего и нижнего допустимых значений, а основного параметра объекта - от заданного значения и одновременно отключают управляющее воздействие астатического регулятора внешнего контура, формируют и сохраняют интегральную составляющую этого регулятора на уровне значения средней позиции выходного сигнала регулятора внутреннего контура, при возврате вспомогательного параметра объекта в заданный интервал одновременно отключают управляющее воздействие регулятора внутреннего контура и включают управляющее воздействие астатического регулятора внешнего контура.

Способ решает поставленные перед ним задачи, но, будучи построенным на релейном принципе работы, в некоторых случаях (например, при гармоническом виде возмущений) может привести к возникновению режима автоколебаний. Кроме этого способ теряет свою работоспособность при отсутствии возможности измерения вспомогательного параметра, который в данном случае должен быть представлен моментом нагрузки на валу двигателя электромеханической системы.

Известен способ регулирования скорости и тока в электромеханической системе с электроприводом постоянного тока (источник книга Чиликин М.Г., Ключев В.И., Сандлер А.С. Теория автоматизированного электропривода: Учеб. пособие для вузов. - М.: Энергия, 1979. - 616 с. (стр. 280, рис. 6-15)). Способ является примером построения системы подчиненного регулирования и заключается в том, что регулирование нескольких переменных в системе электропривода производят путем измерения скорости и тока двигателя постоянного тока, сравнения измеренного значения скорости с заданным и подаче сигнала рассогласования на регулятор скорости. Результирующее значение на выходе регулятора скорости считают задающим для регулятора тока, на который подают сигнал обратной связи по току. При этом влияние возможных колебаний момента нагрузки на вал исполнительного двигателя постоянного тока оценивают путем измерения выходного параметра (в данном случае - скорости). Тем самым компенсацию возмущения осуществляют после его воздействия на выходной параметр.

Способ выполняет возложенные на него функции, но имеет существенный недостаток, заключающийся в том, что при необходимости компенсации влияния флуктаций момента нагрузки на выходную переменную (скорость исполнительного механизма) приходится значительно повышать быстродействие (динамическую точность) системы путем повышения коэффициента петлевого усиления. Это может привести к существенному ухудшению качества отработки управляющего воздействия или повышению токовых форсировок и соответствующему сокращению размеров линейной зоны работы системы, имеющей ограничение мощности силовых исполнительных органов.

Наиболее близким к заявляемому является известный способ компенсации возмущений в установившемся режиме, именуемый как «принцип внутренней модели» (источник книга Гудвин Г.К. Проектирование систем управления / Гудвин Г.К., Гребе С.Ф., Сальгадо М.Э. - М.: БИНОМ, Лаборатория знаний, 2004. - 911 с. (стр. 284-285)), принятый за прототип, который заключается в том, что управление осуществляют регулятором по скорости рабочего органа, для чего предварительно по результату анализа спектрограммы скоростей электромеханической системы, выделяют частоту наиболее существенного возмущения, с учетом этой частоты находят полином, формирующий математическую модель гармонического возмущения момента нагрузки, вводят этот полином сомножителем в знаменатель передаточной функции регулятора по скорости рабочего органа, а искажение передаточной функции электромеханической системы по управлению устраняют за счет воздействия внеконтурного формирователя.

При этом выходной сигнал регулятора по скорости рабочего органа будет содержать гармоническую составляющую, которая благодаря действию отрицательной обратной связи по скорости рабочего органа, замыкающей внешний контур регулирования, обеспечит противофазную компенсацию возмущения. Следует отметить, что регулятор и внеконтурный формирователь реализованы в виде материальных объектов (цифровых или аналоговых блоков), которые при наладке требуют установки внутренних параметров, соответствующих полиномам, синтезированным в процессе конструирования системы управления. Способ, выбранный за прототип, выполняет свои основные функции, требует измерения лишь выходной координаты объекта управления - угловой скорости вала рабочего органа.

Основными недостатками предложенного технического решения являются недостаточная динамическая точность и высокие аппаратные или программные ресурсы, необходимые для реализации системы.

Структурная схема, иллюстрирующая работу способа-прототипа применительно к электромеханической системе с двигателем постоянного тока, приведена на фиг. 1. В состав структурной схемы введены внеконтурный формирователь 1, представляющий собой префильтр и предназначенный для устранения искажения передаточной функции электромеханической системы по управлению; первый элемент сравнения 2, который формирует на своем выходе сигнал ошибки, управляющий регулятором 3. Регулятор 3 замыкает отрицательную обратную связь по скорости рабочего органа и выполнен в виде блока, передаточная функция которого представляется отношением полиномов. Кроме этого в составе системы имеется силовой преобразователь 4, который преобразует напряжение управления Uy на своем входе в напряжение U на якорной обмотке электродвигателя постоянного тока 5. Измерительный блок 6 предназначен для измерения скорости электродвигателя постоянного тока 5. Регулятор 3 и внеконтурный формирователь 1 реализованы в виде материальных объектов (цифровых или аналоговых блоков), которые при наладке требуют установки внутренних параметров, соответствующих полиномам, синтезированным в процессе конструирования системы управления.

В качестве основных параметров, влияющих на работоспособность системы, часть из которых приведена на фиг. 1, выбраны:

- напряжение, определяющее заданное значение скорости рабочего органа;

- напряжение после внеконтурного формирователя;

U_y, U - управляющее и выходное напряжение силового преобразователя;

I_a - ток якорной цепи электродвигателя постоянного тока;

Ω - угловая скорость вала электродвигателя постоянного тока;

Ωн - номинальная угловая скорость вала электродвигателя постоянного тока;

М_Н - момент нагрузки (статического сопротивления).

Также здесь и далее приняты следующие обозначения параметров системы:

К_СП и Т_СП - коэффициент передачи и постоянная времени силового преобразователя;

R_a и Т_а - активное сопротивление и постоянная времени якорной цепи электродвигателя постоянного тока;

С - конструктивная постоянная двигателя постоянного тока;

J - суммарный момент инерции ротора двигателя постоянного тока и рабочего органа;

i - передаточное отношение редуктора.

Система имеет полиномиальный регулятор 3, в знаменатель передаточной функции которого введена, как показано выше, модель возмущения. Попытаемся синтезировать структуру регулятора 3 для электромеханической системы, построенной с применением двигателя постоянного тока 5, управляемого от силового преобразователя 4.

Для конкретности приняты следующие значения параметров объекта: К_СП=22, Т_СП=0,001 с, Ra=0,177 Ом, Та=0,02 с, Ωн=157 рад/с, С=1,37 Вб, J=0,2 кг⋅м², i=10.

Пусть требуется обеспечить пуск электромеханической системы (ЭМС) на заданный уровень скорости Ω вала двигателя постоянного тока 5, равный 15,7 рад/с, что составляет 10% от номинальной скорости при монотонном характере переходного процесса и времени нарастания переходной характеристики системы в линейной зоне ее работы не более 50 мс. После пуска системе необходимо отработать возмущающее воздействие момента нагрузки, соответствующее уравнению (1) вида

при отсутствии перерегулирования, обеспечив заданное быстродействие и нулевую статическую ошибку по скорости от действия момента нагрузки.

Согласно принципу селективной инвариантности, полином, формирующий математическую модель возмущения (1), определяется в данном случае в виде

где s - комплексная переменная Лапласа, ω₁=Ω/i - угловая скорость рабочего органа. Этот полином вводится сомножителем в знаменатель передаточной функции (ПФ) регулятора 3, а искажение передаточной функции ЭМС по управлению устраняется соответствующим внеконтурным формирователем 1. Регулятор 3 с такой моделью возмущения приобретает интегральную s и колебательную (s²+ω₁²) составляющие, которые в условиях действия отрицательной обратной связи (ОС) в совокупности обеспечивают астатизм 1-го порядка, т.е. нулевую статическую ошибку от действия постоянной составляющей момента, и противофазную компенсацию его гармонической составляющей в установившемся режиме работы. Появление дополнительных нулей ПФ системы по управляющему воздействию устраняется соответствующим внеконтурным формирователем 1 (префильтром).

Объектом управления в данной системе являются последовательно соединенные силовой преобразователь 4 и электродвигатель постоянного тока 5. Передаточная функция объекта управления может быть представлена в виде отношения полиномов B(s) и A(s).

Для повышения робастных свойств синтезируемых систем автоматического управления (исключения появления положительных ОС или неминимально-фазовых звеньев в составе регуляторов) пренебрежем в расчетах относительно малой постоянной времени Т_СП. В результате этого ПФ объекта управления принимает вид с передаточной функцией

Для полученной ПФ объекта управления по правилам полиномиального модального управления рассчитывают регулятор, используя уравнение

где R(s) и s⋅C(s) - полиномы числителя и знаменателя ПФ регулятора, причем R(s)=G(s)⋅V(s), V(s) - вспомогательный полином, обеспечивающий техническую реализуемость регулятора, D(s) - желаемый характеристический полином (ХП) синтезируемой системы.

Для этого в соответствии с заданными требованиями динамики формируют структуру и определяют параметры регулятора 3

Использование передаточной функции объекта управления обеспечивает более полный учет его особенностей и способствует повышению помехоустойчивости и параметрической грубости системы.

Как видно из приведенного соотношения, порядок регулятора 3 с учетом внеконтурного формирователя 1 - восьмой. Это подтверждает наличие у прототипа недостатка в виде повышенной сложности при технической реализации как в цифровой, так и в аналоговой форме, что неизбежно приводит к высоким аппаратным или программным затратам.

На фиг. 2 приведены результаты проведенного компьютерного моделирования прототипа с синтезированным регулятором 3. Они представлены переходным процессом угловой скорости Ω вала электродвигателя постоянного тока 5. В процессе исследования осуществляется пуск электродвигателя постоянного тока 5 на заданную скорость Ω, равную 10% от номинальной, что при известных параметрах системы составляет 15,7 рад/с. С учетом выбранного передаточного отношения редуктора i=10 это соответствует угловой скорости рабочего органа ω₁=1,57 рад/с. После завершения переходного процесса пуска к валу электродвигателя постоянного тока 5 прикладывается момент нагрузки М_Н выбранного вида . Здесь и далее внешнее возмущение в виде изменения момента нагрузки воздействует на вал электродвигателя в момент t=4 с. Анализ переходной характеристики указывает на удовлетворительное качество процесса пуска. Система обеспечивает заданное время нарастания переходной характеристики в линейной зоне ее работы не более 50 мс при отсутствии перерегулирования. При воздействии внешнего возмущения обеспечивается достаточное быстродействие, но наблюдается значительная динамическая ошибка 0,62 рад/с при отработке наброса момента нагрузки заданного вида.

Итак, выполняя возложенные на нее задачи, система демонстрирует недостаточную динамическую точность, обладает повышенной сложностью технической реализации регулятора. Последнее требует больших аппаратных или программных затрат при построении регулятора восьмого порядка как в аналоговой, так и в цифровой формах, снижает надежность системы, создает дополнительные проблемы при настройке системы на реальном объекте.

Технический результат предлагаемого изобретения заключается в улучшении динамической точности и сокращении аппаратных или программных затрат при технической реализации системы.

Технический результат достигается тем, что в способе устранения влияния гармонических возмущений момента нагрузки в электромеханической системе, заключающемся в том, что управление осуществляют внешним контуром регулирования по скорости рабочего органа, для чего предварительно по результату анализа спектрограммы скоростей электромеханической системы выделяют частоту наиболее существенного возмущения, с учетом этой частоты находят полином, формирующий математическую модель гармонического возмущения момента нагрузки, используют этот полином при формировании передаточной функции внешнего контура регулирования по скорости рабочего органа, а искажение передаточной функции внешнего контура системы по управлению устраняют за счет воздействия первого внеконтурного формирователя, математическую модель гармонического возмущения разделяют на интегральную и колебательную составляющие, колебания момента нагрузки дополнительно компенсируют по внутреннему контуру, представляющему собой полиномиальный регулятор, искажение передаточной функции внутреннего контура системы по управлению устраняют за счет воздействия второго внеконтурного формирователя, при формировании передаточных функций полиномиального регулятора внутреннего контура и второго внеконтурного формирователя используют колебательную составляющую математической модели гармонического возмущения, а интегральную часть математической модели гармонического возмущения учитывают при формировании передаточных функций полиномиального регулятора внешнего контура и первого внеконтурного формирователя, при этом передаточные функции элементов системы настраивают в два этапа, на первом из которых по желаемому полиному внутреннего контура, исходя из быстродействия в 5-7 раз выше заданного для системы в целом, определяют параметры элементов внутреннего контура и второго внеконтурного формирователя, а на втором этапе по заданному быстродействию и желаемому характеристическому полиному синтезируемой системы формируют передаточные функции регулятора внешнего контура и внеконтурного формирователя.

На фиг. 3 изображена блок-схема устройства, поясняющего работу предложенного способа, на фиг. 4 приведены результаты компьютерного моделирования работы устройства, реализующего заявляемый способ при тех же условиях и тех же режимах, которые выбраны для способа-прототипа.

Для фиг. 3 введены следующие обозначения: первый внеконтурный формирователь 1, подключенный к неинвертирующему входу первого элемента сравнения 2, выход которого соединен со входом регулятора внешнего контура 3; силовой преобразователь 4, преобразующий свой входной сигнал U_y в напряжение U на якорной обмотке электродвигателя постоянного тока 5. Измерительный блок 6 выполнен с возможностью оценивания скорости двигателя постоянного тока 5. Для этого скорость электродвигателя постоянного тока 5 измеряется и преобразуется в напряжение U_Ω, пропорциональное скорости электродвигателя постоянного тока 5. В состав блок-схемы введен второй внеконтурный формирователь 7, вход которого соединен с выходом регулятора внешнего контура 3, а выход - с неинвертирующим входом второго элемента сравнения 8. К инвертирующему входу второго элемента сравнения 8 подключен выход измерительного блока 6, а выход второго элемента сравнения 8 через регулятор внутреннего контура 9 подключен ко входу силового преобразователя 4.

Способ осуществляют следующим образом. Первоначально для выбранной электромеханической системы производят снятие и исследование спектрограммы скоростей. Если спектрограмма была построена ранее, пользуются результатами проведенных исследований. На спектрограмме выделяют частоту наиболее существенного воздействия, которое приводит к возникновению доминирующего гармонического возмущения момента нагрузки на валу рабочего органа. По известной кинематической схеме механизма и выявленной частоте находят соответствующую угловую скорость рабочего органа ω₁, которая позволяет вычислить математическую модель наиболее существенного возмущения, соответствующую уравнению (2). При этом в отличие от способа-прототипа, полином (3), формирующий постоянную и колебательную составляющие математической модели возмущения (2), делится на интегральную и колебательную составляющие: s и (s²+ω₁²) соответственно.

Для достижения поставленного технического результата и организации процесса управления в состав системы кроме известного внешнего контура регулирования по основной координате (в данном случае - по скорости рабочего органа или жестко связанной с ней скорости электродвигателя постоянного тока) вводят внутренний контур регулирования.

Внешний контур регулирования построен по принципу полиномиального регулятора (ПР) по основной координате объекта управления - скорости электродвигателя постоянного тока 5 и организован с учетом интегральной составляющей математической модели возмущения. Внутренний контур, представляющий собой также полиномиальный регулятор (ПР), синтезируется с учетом колебательной составляющей математической модели возмущения и настраивается на быстродействие, в 5-7 раз превышающее заданные динамические требования, предъявляемые ко всей системе в целом. Этим обеспечивается максимальное упрощение внешнего интегрального контура регулирования при соответствующем упрощении структуры первого внеконтурного формирователя 1 и улучшение качества отработки переменной составляющей момента нагрузки электродвигателя постоянного тока 5. Для реализации принципа селективной инвариантности такой электромеханической системы в ее внешнем и внутреннем контурах управления используются только полиномиальные регуляторы «входа-выхода».

Процедура настройки системы производится в направлении от внутреннего контура к внешнему. Синтез регулятора внутреннего контура 9 заключается в определении коэффициентов полиномов F(s) и E(s) регулятора, для чего используется следующее уравнение полиномиального синтеза

где A(s) и B(s) - характеристический полином и полином воздействия передаточной функции объекта управления (электродвигателя постоянного тока 5);

F(s) и E(s) - полиномы знаменателя и числителя передаточной функции регулятора внутреннего контура 9;

F(s)=G(s)⋅V(s);

V(s) - вспомогательный полином, обеспечивающий техническую реализуемость регулятора;

P(s) - желаемый характеристический полином синтезируемого внутреннего контура.

В нашем случае в полином знаменателя F(s) передаточной функции регулятора внутреннего контура 9 вводится колебательная составляющая математической модели возмущения

.

Для синтеза полиномиального регулятора внешнего контура 3, учитывающего интегральную составляющую модели возмущения, используется следующее полиномиальное уравнение

где P(s) и Q(s) - характеристический полином и полином воздействия передаточной функции регулятора внутреннего контура 9;

C(s) и R(s) - полиномы знаменателя и числителя передаточной функции регулятора внешнего контура 3;

D(s) - желаемый характеристический полином синтезируемой системы.

Выбранное высокое быстродействие регулятора внутреннего контура 9, содержащего колебательную составляющую модели возмущения, дает основание считать его безынерционным при синтезе регулятора внешнего контура 3, т.е. принимать: Q(s)=K, P(s)=1, что значительно упрощает регулятор внешнего контура 3.

Первый внеконтурный формирователь 1 и второй внеконтурный формирователь 7 внешнего и внутреннего контуров соответственно исключают искажение по управлению передаточных функций указанных контуров системы. Для выполнения своих функций их передаточные функции выбирают обратнопропорциональными числителям передаточных функций регуляторов внешнего контура 3 (R(s)) и внутреннего контура 9 (E(s)).

Проведем формирование элементов электромеханической системы путем синтеза регуляторов в направлении от внутреннего контура к внешнему, воспользовавшись теми же числовыми параметрами объекта управления и заданными требованиями к быстродействию системы, что и в прототипе.

Методом модального управления по уравнению синтеза (8) рассчитывается передаточная функция регулятора внутреннего контура 9, наделяемого быстродействием, в 5 раз превышающим заданное значение быстродействия системы, и содержащего колебательную составляющую модели возмущения. При заданном быстродействии системы в 50 мс это соответствует быстродействию внутреннего контура в 10 мс. В качестве желаемого для внутреннего контура принимается характеристический полином Ньютона 5-го порядка P(s)=(s+900)⁵ с величиной среднегеометрического корня Ω_0Б=900 с^-1, что соответствует выбранному быстродействию внутреннего контура. Полином P(s) наиболее соответствует монотонному переходному процессу, что отвечает требованиям к качеству переходных процессов в системе и удобно для дальнейшей аппроксимации внутреннего контура звеньями пониженного порядка. В этом случае уравнение (8) принимает следующий развернутый вид

.

Его решение позволяет получить передаточную функцию регулятора внутреннего контура 9 следующего вида

.

Второй внеконтурный формирователь 7 внутреннего контура по аналогии со способом-прототипом устраняет появление дополнительных нулей передаточной функции системы по управляющему воздействию. Передаточная функция второго внеконтурного формирователя 7 выбирается с учетом передаточной функции регулятора внутреннего контура 9 и принимает вид

.

Для расчета регулятора внешнего контура с интегральной составляющей модели возмущения используется полиномиальное уравнение синтеза (9).

Высокое быстродействие внутреннего контура дает основание считать его безынерционным при синтезе регулятора внешнего контура 3, т.е. принимать: (b₀ - свободный коэффициент передаточной функции объекта управления, Ω_0Б - среднегеометрический корень регулятора внутреннего контура), P(s)=1. Выбор полинома D(s) для внешнего контура производится из тех же соображений, что и полинома P(s) для внутреннего контура системы. В соответствии с заданными требованиями динамики в качестве D(s) выбирается полином Ньютона 1-го порядка D(s)=(s+20) с величиной среднегеометрического корня Ω₀=20 с^-1, что соответствует заданному быстродействию системы в 50 мс.

В этом случае уравнение синтеза (9) принимает наиболее простой вид

1⋅s+7,2094⋅10^-11⋅r₀=s+20.

Его решение позволяет получить передаточную функцию регулятора внешнего контура 3 минимального порядка следующего вида

.

Передаточная функция первого внеконтурного формирователя 1 внешнего контура также выбирается с учетом передаточной функции регулятора внешнего контура 3 и в данном случае упрощается до коэффициента усиления, т.е. принимает вид

.

Полученные значения позволяют выбрать параметры аналоговых или цифровых блоков системы при ее технической реализации.

Таким образом, порядок передаточной функции системы, организованной путем использования заявляемого способа с учетом порядков передаточных функций первого и второго внеконтурного преобразователей - седьмой.

Применение последовательности операций, характерных для заявляемого способа, привело к упрощению регулятора, что при его технической реализации аналоговыми или цифровыми устройствами сокращает аппаратные или программные затраты. Это неизбежно приводит к повышению надежности, а при внедрении сокращает время наладки.

Проанализируем результаты компьютерного моделирования синтезированного регулятора при тех же параметрах объекта, что и для способа прототипа.

Анализ фиг. 4 доказывает высокую эффективность работы системы при пуске, сопоставимую с результатами компьютерного моделирования способа-прототипа, приведенными на фиг. 2. При приложении внешнего возмущающего момента нагрузки после 4 секунды работы на установившейся скорости в 15,7 рад/с наблюдается существенное по сравнению с прототипом снижение динамической ошибки до 0,16 рад/с, что подтверждает улучшение динамической точности заявленной системы.

Компенсация влияния возникающих колебаний момента нагрузки по рассматриваемому варианту способа осуществляется за счет того, что при возникновении таких колебаний происходит изменение угловой скорости вала электродвигателя постоянного тока 5, которое, будучи введено в виде отрицательной обратной связи на вход регулятора внешнего контура 3, и на вход регулятора внутреннего контура 9, настроенных на гашение заданной частоты, компенсируется внешним и внутренним контурами системы автоматического управления. Внутренний контур системы, настроенный на высокое быстродействие в 5-7 раз выше заданного, обеспечивает эффективную отработку возмущения, низкий порядок регулятора. Внешний контур, использующий интегральную составляющую регулятора внешнего контура 3, способствует улучшению динамической точности.

Предлагаемое техническое решение позволяет улучшить динамическую точность и сократить аппаратные или программные затраты при технической реализации системы.

Способ устранения влияния гармонических возмущений момента нагрузки в электромеханической системе, заключающийся в том, что управление осуществляют внешним контуром регулирования по скорости рабочего органа, для чего предварительно по результату анализа спектрограммы скоростей электромеханической системы выделяют частоту наиболее существенного возмущения, с учетом этой частоты находят полином, формирующий математическую модель гармонического возмущения момента нагрузки, используют этот полином при формировании передаточной функции внешнего контура регулирования по скорости рабочего органа, а искажение передаточной функции внешнего контура системы по управлению устраняют за счет воздействия первого внеконтурного формирователя, отличающийся тем, что математическую модель гармонического возмущения разделяют на интегральную и колебательную составляющие, колебания момента нагрузки дополнительно компенсируют по внутреннему контуру, представляющему собой полиномиальный регулятор, искажение передаточной функции внутреннего контура системы по управлению устраняют за счет воздействия второго внеконтурного формирователя, при формировании передаточных функций полиномиального регулятора внутреннего контура и второго внеконтурного формирователя используют колебательную составляющую математической модели гармонического возмущения, а интегральную часть математической модели гармонического возмущения учитывают при формировании передаточных функций полиномиального регулятора внешнего контура и первого внеконтурного формирователя, при этом передаточные функции элементов системы настраивают в два этапа, на первом из которых по желаемому полиному внутреннего контура, исходя из быстродействия в 5-7 раз выше заданного для системы в целом, определяют параметры элементов внутреннего контура и второго внеконтурного формирователя, а на втором этапе по заданному быстродействию и желаемому характеристическому полиному синтезируемой системы формируют передаточные функции регулятора внешнего контура и внеконтурного формирователя.