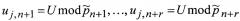Способ безопасного кодирования информации для ее передачи по открытым каналам связи методами стеганографии

Способ безопасного кодирования информации для ее передачи по открытым каналам связи методами стеганографии

Иллюстрации

Показать все

Реферат

Изобретение относится к области телекоммуникаций и предназначено для скрытой передачи информации.

Известен способ криптографического преобразования [ГОСТ 28147-89. Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования. - М.: Госстандарт СССР, 1989], реализующий алгоритм блочного шифрования информации с фиксированной длиной блока, равной 64 битам, длиной ключа 256 бит, предусматривающий три режима шифрования: простой замены, гаммирования, гаммирования с обратной связью и дополнительный режим выработки имитовставки.

Недостатком данного способа является незащищенность от воздействия случайных искажений (помех) возможных в канале связи при передаче криптограмм.

Известен способ безопасной передачи конфиденциальных данных по нескольким каналам [Belal А.А., Abdelhamid A.S. Secure transmission of sensitive data using multiple channels, The 3^rd ACS/IEEE International Conference, Computer Systems and Applications, 2005. - Режим доступа: http://arxiv.org/ftp/cs/papers/0403/0403023.pdf], заключающийся в том, исходное сообщение делится на блоки, и называют их суперблоками, каждый их которых шифруется одним из алгоритмов блочного шифрования. Каждый из полученных суперблоков криптограммы рассматривают как целое битовое число N. Множество S попарно простых модулей q₀, q₁, …, q_s-1 выбраны таким образом, что . Целое битовое число N на основании Китайской теоремы об остатках представляется своими наименьшими неотрицательными вычетами r₀, r₁ ,…, r_s-1, при r_i=N mod q_i, i=0,1, …, S-1. Полученные таким образом S вычетов передают по S отобранным каналам связи, причем незадействованная в передаче вычетов часть каналов несет некоторые несоответствующие данные, в целях уменьшения способности противника определить используемые каналы.

Недостатком известного способа является невозможность восстановления всего блока передаваемой криптограммы при потере (искажении) одного или нескольких вычетов вследствие воздействия помех.

Известен способ стеганографического сокрытия информации [Патент RU 2374770, H04L 9/00, 2009 г.], заключающийся в том, что открытый текст шифруют методами многоалфавитной замены и методом перестановок. Полученную криптограмму скрывают в графическом контейнере, при этом изображение каждого символа криптограммы формируют с помощью матрицы размером n×m цифровой форме из w информативных, r пограничных и q маскирующих точек, которые перемешивают различными способами. Далее выбирают графических или иных контейнеров, в которые побитно распыляют информацию из перемешанных графических матриц по s контейнерам, в d контейнеров помещают ложную информацию, а контейнеров оставляют пустыми.

Недостатком указанного способа является невозможность полноценного восстановления информации на принимающей стороне при искажении одного или нескольких контейнеров (в результате помех или атак против встроенного сообщения).

Наиболее близким из аналогов (прототипом) является способ скрытой передачи зашифрованной информации по множеству каналов связи [Патент RU 2462825, H04L 9/00, 2012 г.], заключающийся в том, что открытый текст разбивают на блоки, каждый блок шифруют с помощью шифра со сцеплением блоков на ключе k₁, получая криптограмму C₁, состоящую из m блоков и повторно шифруют шифром на ключе k₂, получая криптограмму C₂, состоящую из r блоков, далее полученные блоки стеганографически скрывают в r контейнерах различного типа с использованием ключа k₃, который определяет тип контейнера и секретные параметры алгоритмов внедрения. Полученные r контейнеров со встроенной информацией пересылают по нескольким каналам связи в соответствии с ключом k₄. При организации связи используют S=S_c+S_m доступных каналов связи, где в текущем сеансе связи с помощью ключа k₄ выделяют не все, а только часть доступных каналов связи S_c, по всем доступным каналам S=S_c+S_m непрерывно передают камуфлирующие сигналы, а полезную информацию передают в псевдослучайные моменты времени.

Недостатками указанного способа являются: во-первых, помехоустойчивость передачи шифрованной информации достигается за счет дублирования передачи информации по разным каналам связи, что вносит избыточность, равную объему передаваемых данных и увеличивает время, затрачиваемое на передачу информации; во-вторых, деструктивные воздействия на хотя бы один из контейнеров, приводят к невозможности полноценного восстановления переданной информации.

Техническим результатом данного изобретения является повышение помехоустойчивости передаваемой информации. Изобретение позволяет на принимающей стороне восстановить переданное сообщение целиком при потере не более заданного количества контейнеров.

Сущность предлагаемого способа безопасного кодирования информации для ее передачи по открытым каналам связи методами стеганографии заключается в том, что осуществляют обмен между корреспондентами секретными ключами K_шифр и K_стег. Открытое сообщение M_j может быть предварительно зашифровано одним из известных криптоалгоритмов с использованием ключа шифрования K_шифр. Вместе с ключами корреспонденты осуществляют обмен двумя таблицами пронумерованных попарно простых модулей (оснований), таблица №1 - V информационных модулей и №2 - Z служебных модулей. Выполняют анализ поступающих Z контейнеров, на основании которого определяют максимальное количество бит (отсчетов) одного контейнера, обеспечивающее безопасное встраивание информации методами стеганографии. В резервируется место (фиксированное количество бит), необходимое для встраивания служебной информации . Осуществляют перегруппировку полученного массива, элементами которого станут значения L_j,i так, что r максимальных L_j,i, выстраивают справа по возрастанию, а порядок следования n оставшихся L_j,i оставляют без изменения. Из таблицы №1 производят выбор n попарно простых модулей по условию , а r проверочных модулей выбирают следующие по порядку, по возрастанию , где - номера модулей из таблицы №1. Далее получают информационные вычеты , так что фрагмент передаваемой информации C_j есть результат конкатенации n вычетов , и получают избыточные вычеты . По n известным номерам модулей выполняют расширение модулярного кода, принимая номера модулей, за вычеты модулярного кода. По системе попарно простых модулей из таблицы №2, находят избыточные вычеты: . Далее определяют номера контейнеров, которым соответствуют избыточные вычеты и порядок их следования в модулярном коде . Объединяют полезную и служебную информации, формируя, тем самым, двоичные блоки и выполняют обратную сортировку блоков , восстанавливая порядок их следования в соответствии с естественным порядком следования контейнеров . По ключу для стеганографического преобразования K_стег встраивают информационные блоки в Z контейнеров методами стеганографии, передают их в канал связи.

Благодаря новой совокупности существенных признаков в способе реализована возможность безопасного кодирования информации, представляемой в модулярном коде (МК), где выбор модулей и количество кодируемых бит, подлежащих встраиванию в контейнеры методами стеганографии, определяются на основе энтропийного анализа контейнеров, чем достигается повышение помехоустойчивости передаваемых данных, за счет возможности МК обнаруживать (исправлять) q искажений.

Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности «новизна».

Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность отличительных существенных признаков, обуславливающих тот же технический результат, который достигнут в заявляемом способе. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».

Заявленное изобретение поясняется чертежами, на которых показано:

фиг. 1 - структурное представление предлагаемого способа на передающей стороне (I уровень кодирования) (часть 1);

фиг. 2 - структурное представление предлагаемого способа на передающей стороне (I уровень кодирования) (часть 2)

фиг. 3 - схема встраивания информации в контейнеры;

фиг. 4 - структурное представление предлагаемого способа на передающей стороне (II уровень кодирования);

фиг. 5 - структурное представление предлагаемого способа на передающей стороне (III уровень кодирования) (часть 1);

фиг. 6 - структурное представление предлагаемого способа на передающей стороне (III уровень кодирования) (часть 2);

фиг. 7 - информационные и проверочные блоки, подлежащие встраиванию в контейнеры;

фиг. 8 - структурное представление предлагаемого способа на принимающей стороне (III уровень декодирования);

фиг. 9 - структурное представление предлагаемого способа на принимающей стороне (II уровень декодирования);

фиг. 10 - структурное представление предлагаемого способа на принимающей стороне (I уровень декодирования);

фиг. 11 - зависимость вероятности недостоверного приема всего сообщения P_q от вероятности возникновения искажения стеганографического контейнера p, при r=0 слева и r=1 справа;

фиг. 12 - зависимость вероятности недостоверного приема всей криптограммы P_q от вероятности возникновения искажения стеганографического контейнера p, при r=2 слева и r=3 справа.

Предлагаемый способ использует следующие положения теории чисел и теории кодирования:

Согласно [Бояринов И.М. Помехоустойчивое кодирование числовой информации. - М: Наука, 1983. Стр. 48-49] любое целое число C_i≥0 однозначно представляется в МК последовательностью , где c_i=C_i mod p_i, i=1,2,…,k. Основаниями данной системы служат попарно простые числа p₁,p₂,…,p_k, такие что C_i<P, где . Числа c_i представляются любым способом, например в двоичной системе счисления.

На основании Китайской теоремы об остатках [Бояринов И.М. Помехоустойчивое кодирование числовой информации. - М.: Наука, 1983. Стр. 49; Бухштаб А.А. Теория чисел. - М.: Просвещение, 1966. Стр. 123] система вычетов:

имеет единственное решение C_i, если выполнены вышеуказанные условия. Единственное решение системы (1) дает выражение:

,

где , , .

В соответствии с [Бояринов И.М. Помехоустойчивое кодирование числовой информации. - М.: Наука, 1983. Стр. 50-51; Акушский И.Я., Юдицкий Д.И. Модулярная арифметика в остаточных классах. - М.: Сов. Радио, 1968. Стр. 158-160] операция расширения полученного модулярного кода (РМК) путем введения избыточных оснований и получения избыточных вычетов , предполагая, что

выполняется в целях повышения помехоустойчивости, а условие:

где - возможно содержащая ошибки криптограмма C_i, является ключевым условием определения наличия (отсутствия) обнаруживаемых ошибок в принятой последовательности [Бояринов И.М. Помехоустойчивое кодирование числовой информации. - М.: Наука, 1983. Стр. 50-51; Акушский И.Я., Юдицкий Д.И. Модулярная арифметика в остаточных классах. - М.: Сов. Радио, 1968. Стр. 158-160].

Предлагаемый способ, функционирующий на приемной и передающей сторонах, условно разделен на три части, в каждой из которых реализуется один из трех уровней кодирования информации:

- на первом уровне кодируется полезная информация (информационные и избыточные вычеты модулярного кода);

- на втором уровне кодируется служебная информация в виде номеров модулей таблицы №1;

- на третьем кодируются номера контейнеров с избыточной информацией с сохранением порядка их следования в МК.

Соответственно, на принимающей стороне, декодирование производится в обратном порядке.

Осуществление изобретения

На приемной и передающей сторонах имеются секретные ключи K_шифр и K_стег, а также две таблицы пронумерованных попарно простых модулей (оснований) №1: и №2: . Причем модули таблицы №2 имеют порядок значительно меньший, чем модули таблицы №1. Открытый текст M_j может быть предварительно зашифрован одним из известных криптоалгоритмов с использованием ключа шифрования K_шиф. В результате получают криптограмму C_j, которая и будет подлежать передаче предлагаемым способом.

На следующем шаге (или параллельно с предыдущим) выполняют анализ поступающих контейнеров (фиг. 1, 2). Здесь анализируют формат контейнеров (jpeg, bmp, tiff, mp3, avi, wav и т.п.), а также выполняют анализ содержимого контейнеров (энтропийный анализ). На основании проведенного анализа и исходя из требований, предъявляемых к стеганографическому каналу передачи данных, определяют количество бит , при i=1,2,…, Z, которые можно безопасно встроить в контейнер с заданной стеганографической стойкостью. Такой анализ может проводиться заблаговременно на основе изучаемых параметров (например: формат контейнера, объем и др.). По результатам анализа формируется типовая таблица, которую в дальнейшем используют с целью ускорения процесса анализа. Методика оценки контейнера приведена в [Грибунин В.Г., Оков К.Н., Туринцев И.В. Цифровая стеганография. - М.: Солон-Пресс, 2009. Стр. 110-154]. В резервируется место (фиксированное количество бит), таким образом, что , где - фактическое количество бит, которые можно встроить в данный стегоконтейнер с заданной стеганографической стойкостью, - количество бит (фиксированное), необходимых для встраивания служебной информации.

Далее производят поиск r максимальных элементов L_j,i вычисляя max при , n+r=Z, где r - фиксированное количество, соответствующее избыточным контейнерам. Полученные избыточные значения сортируются по возрастанию, а оставшиеся n информационных значений, сдвигаются без изменения порядка их следования, при этом данные о первоначальном значении порядковых номеров (соответствующих естественному порядку следования контейнеров) сохраняются.

На следующем шаге, по полученным значениям предельного количества бит, из таблицы №1 производят выбор попарно простых модулей по условию , при этом , где i и d=1, 2,…, Z; - округление до целого. В свою очередь, модули от 1 до n выбираются в соответствии с условием (необязательно подряд), а от n до n+r выбираются следующие по порядку, так что каждый последующий будет больше предыдущего . Значения - номера модулей из таблицы №1, которым ставится в соответствие номера контейнеров.

На следующем этапе получают информационные вычеты . Фрагмент передаваемой информации C_j есть результат конкатенации n вычетов , которые подлежат встраиванию в n контейнеров, - знак конкатенации. Здесь и далее двоичные информационные последовательности блоков конкатенации , где , , будем трактовать, как вычеты МК.

Имея информационные вычеты и систему попарно простых модулей , производят операцию расширения модулярного кода, получая избыточные вычеты, реализуя первый уровень кодирования. Путем решения Китайской теоремы об остатках по системе попарно простых модулей получают: , и вычисляют избыточные вычеты:

.

Для понимания рассмотрим простой пример представления криптограммы в РМК, не принимая во внимание условие: .

Пусть требуется передать криптограмму - «СЕКРЕТ». Представим текст в двоичной форме в соответствии с таблицей ASCII (таблица 1.)

Выполним операцию конкатенации, получаем:

или:

Представим данное число в МК по системе попарно простых модулей , , , , , , , убедимся, что рабочий диапазон больше криптограммы (C_j<P), по формуле получаем Р=14630623025683019, условие выполнено, следовательно, криптограмму C_j можно единственным образом представить в МК. По формуле , получаем C_j=(16, 41, 24, 17, 44, 557, 41765)_МК.

На следующем шаге в соответствии с условием (2) выполним операцию расширения МК, расширим систему модулей на одно основание p₈=94771, получим систему вычетов: C_j=(16, 41, 24, 17, 44, 557, 41765, 41423)_РМК (фиг. 3).

Операция расширения наделяет изобретение свойством гарантированно обнаруживать все одиночные ошибки, если r≥1, и гарантированно исправлять одиночные ошибки, если r≥2 [Бояринов И.М. Помехоустойчивое кодирование числовой информации. - М.: Наука, 1983. Стр. 50-51; Акушский И.Я., Юдицкий Д.И. Модулярная арифметика в остаточных классах. - М.: Сов. Радио, 1968. Стр. 158-160]. Под q-кратной ошибкой понимается произвольное искажение q вычетов c_j,i, в соответствии с [Бояринов И.М. Помехоустойчивое кодирование числовой информации. - М.: Наука, 1983. Стр. 53] МК исправляет q или менее ошибок, если 2q≤r. В нашем примере РМК будет гарантированно обнаруживать все одиночные ошибки.

Далее реализуется второй уровень кодирования (кодирование служебной информации) (фиг. 4). Здесь параллельно этапам вычисления вычетов или последовательно, в зависимости от конкретного алгоритма реализации способа, по n известным номерам модулей и таблице модулей №2 , производят расширение МК, принимая номера модулей , за вычеты некоторого числа U, по системе попарно простых модулей . Вычисляют: , и находят избыточные вычеты . Результатом данного уровня станет представление номеров модулей таблицы №1 в РМК.

На третьем уровне кодирования (фиг. 5, 6) из полученной системы попарно простых модулей определяют номера контейнеров N_j,t, при t=1, 2, …, Z - n и порядок их следования в МК , которым соответствуют избыточные вычеты.

Далее выполняют операцию конкатенации вычетов и служебной информации, формируя, тем самым, двоичные блоки по правилу:

;

Таким образом, получаются блоки ,, подлежащие встраиванию в контейнеры и состоящие из информационных (избыточных) вычетов и служебной информации, где информационные блоки 1, …, n содержат номера модулей , а блоки содержат проверочную информацию, полученную на втором уровне кодирования . Для этого в, как говорилось ранее, резервируется место (фиксированное количество бит), обеспечивающее встраивание служебной информации.

На следующем шаге выполняют обратную сортировку блоков , восстанавливая порядок их следования в соответствии с естественным порядком следования контейнеров и по ключу для стеганографического преобразования K_стег встраивают информационные блоки в контейнеры методами стеганографии (большое число стеганографических методов скрытия информации описано в [Грибунин В.Т., Оков К.Н., Туринцев И.В. Цифровая стеганография. - М.: Солон-Пресс, 2009. Стр. 155-247; Конахович Г.Ф., Пузыренко Ю.А. Компьютерная стеганография: теория и практика. - Киев: МК-Пресс, 2006. Стр. 70-245]), передают их в канал связи.

Для пояснения, ниже представлены две таблицы формирования служебной информации для 5 контейнеров в общем виде (таблица 2) и в частном (таблица 3). Здесь 2 и 5 контейнеры приняты избыточными, причем 2-й контейнер максимальный, поэтому ему соответствует модуль, имеющий порядковый номер 5, а 5-му контейнеру номер 4. Информационным контейнерам - 1, 3, 4, соответствуют номера модулей 2, 3 и 1 из таблицы №1 (информационные модули могут выбираться не по порядку, а исходя из возможностей контейнеров по встраиванию информации). Таким образом, на третьем уровне, в каждый контейнер будут встроены номера контейнеров, соответствующих избыточным модулям, в соответствии с порядком их следования 5, 2.

Блоки α_j,i, подлежащие встраиванию в контейнеры и являющиеся результатом конкатенации информационных (избыточных) вычетов и служебной информации, представлены на фиг. 7.

На принимающей стороне порядок действий следующий (фиг. 8). Приняв Z возможно модифицированных контейнеров , производят обратное стеганографическое преобразование по ключу K_стег и извлекают блоки . Прочитав служебную информацию третьего уровня, выполняют мажоритарное декодирование, в результате получая номера блоков с избыточной информацией и порядок их следования в МК, соответствующие номерам контейнеров , несущих избыточную информацию.

На втором уровне декодирования (фиг. 9) выполняют сортировку блоков с избыточной информацией в соответствии с их номерами, полученными на предыдущем уровне , а блоки с полезной информацией не сортируются, а остаются в том же порядке, как и пришли 99.

Далее извлекают возможно искаженную служебную информацию второго уровня, представленную номерами информационных модулей и их проверочной частью . Решая Китайскую теорему об остатках; , , по системе попарно простых оснований из таблицы №2 , в соответствии с условием , осуществляют контроль ошибок номеров информационных модулей. Выполнение неравенства означает, что принятая последовательность не содержит обнаруживаемых ошибок. Если фиксируется ошибка, осуществляется ее поиск, исправление и заново проверка условия.

Результатом функционирования предлагаемого способа на данном уровне станут возможно исправленные номера информационных модулей таблицы №1, используемые для кодирования полезной информации , а также информационные и избыточные вычеты .

На первом уровне декодирования (фиг. 10) по номерам информационных модулей , полученным на предыдущем уровне, из таблицы №1, получают сами модули , где модули от n до n+r выбираются следующие по порядку, по возрастанию, так как количество избыточных модулей r фиксировано.

Далее, решая КТО ; по системе попарно простых модулей, в соответствии с условием осуществляют контроль ошибок вычетов . Выполнение неравенства означает, что принятая последовательность не содержит обнаруживаемых ошибок. Если фиксируется ошибка, осуществляется ее поиск и исправление.

Результатом данного шага станет массив возможно исправленных вычетов , где r избыточных вычетов отбрасываются. Выполнив операцию конкатенации элементов данного массива , получим переданное сообщение . Пример реализации предлагаемого способа представлен в приложении 1.

Для оценки способности описанного способа верно передавать информацию в условиях деструктивных воздействий злоумышленника введем понятие минимального кодового расстояния РМК D_min. Пусть и - представление чисел М и L в РМК. Назовем весом РМК числа М количество его ненулевых символов (остатков) и обозначим ω(М). Расстояние D между М и L определяется, как вес их разности ω(М-L), Для того чтобы модулярный код исправлял q или менее ошибок, необходимо и достаточно, чтобы минимальное кодовое расстояние кода D_min, удовлетворяло условию: D_min≥2q+1.

Таким образом, представление данных в расширенном модулярном коде позволяет на принимающей стороне восстановить исходное сообщение при полной утрате стегоконтейнеров, число которых не превышает [Бояринов И.М. Помехоустойчивое кодирование числовой информации. - М.: Наука, 1983. Стр. 51]:

,

а передача пустых контейнеров позволяет ввести злоумышленника в заблуждение, не повышая сложности организации и функционирования предлагаемого технического решения.

На фиг. 11 и фиг. 12 графически представлены расчетные данные зависимости вероятности недостоверного приема всего сообщения P_q от вероятности возникновения искажения стеганографического контейнера р, при r=0 слева и r=1 справа при передаче информации методами стеганографии со значениями k=12 и r, принимающих значения от 0 до 3, а вероятность возникновения искажения q изменяется на интервалах [1×10^-5; 0.1] и [1×10^-5; 1×10^-4].

Предлагаемый способ позволяет создать устойчивый скрытый канал обмена конфиденциальной информацией в сети общего пользования, обеспечивающий высокую вероятность достоверной передачи информации методами стеганографии.

Список литературы

1. ГОСТ 28147-89. Системы обработки информации. Защита криптографическая. Алгоритм криптографического преобразования. - М.: Госстандарт СССР, 1989.

2. Belal A.A., Abdelhamid A.S. Secure transmission of sensitive data using multiple channels, The 3^rd ACS/IEEE International Conference, Computer Systems and Applications, 2005. - Режим доступа: http://arxiv.org/ftp/cs/pa-pers/0403/0403023.pdf

3. Патент RU 2374770, H04L 9/00, 2009 г.

4. Патент RU 2462825, H04L 9/00, 2012 г.

5. Бояринов И.М. Помехоустойчивое кодирование числовой информации. - М.: Наука, 1983. - 196 с.

6. Бухштаб А.А. Теория чисел. - М.: Просвещение, 1966. - 384 с.

7. Акушский И.Я., Юдицкий Д.И. Модулярная арифметика в остаточных классах. - М.: Сов. Радио, 1968. - 440 с.

8. Грибунин В.Г., Оков И.Н., Турищев И.В. Цифровая стеганография. - М.: Солон-Пресс, 2009. - 260 с.

9. Конахович Г.Ф., Пузыренко Ю.А. Компьютерная стеганография: теория и практика. - Киев: МК-Пресс, 2006. - 283 с.

Способ безопасного кодирования информации для ее передачи по открытым каналам связи методами стеганографии заключается в том, что осуществляют обмен между корреспондентами секретными ключами K_шифр и K_стег, открытое сообщение M_j может быть предварительно зашифровано с использованием ключа шифрования K_шифр, получают криптограмму C_j, которую далее передают указанным способом, отличающийся тем, что вместе с ключами корреспонденты осуществляют обмен двумя таблицами пронумерованных попарно простых модулей (оснований), таблица №1: p₁, р₂, …, p_V - V информационных модулей, и таблица №2: - Z служебных модулей, выполняют анализ поступающих Z контейнеров, на основании которого определяют максимальное количество бит (отсчетов) одного контейнера, обеспечивающее безопасное встраивание информации методами стеганографии, в резервируется фиксированное количество бит , необходимых для встраивания служебной информации , осуществляют перегруппировку полученного массива, элементами которого станут значения L_j,i таким образом, что r наибольших L_j,i выстраивают справа по возрастанию, а порядок следования n оставшихся L_j,i оставляют без изменения, причем n+r=Z и данные о первоначальном значении порядковых номеров, соответствующих естественному порядку следования контейнеров, сохраняются, из таблицы №1 производят выбор n попарно простых модулей по условию p_j,i>⎡ant log L_j,i⎤, а r проверочных модулей выбирают следующие по порядку, по возрастанию , где χ₁, χ₂, χ₃, …, χ_Z - номера модулей из таблицы №1, далее получают информационные вычеты по правилу: , так что фрагмент передаваемой информации C_j есть результат конкатенации n вычетов C_j=c_j,1|c_j,2|…|c_j,n, и получают избыточные вычеты c_j,n+1, …, c_j,n+r по правилу: , где X_j является решением системы сравнений , () по правилу: , по n известным номерам модулей выполняют расширение модулярного кода, принимая номера χ₁, χ₂, χ₃, …, χ_Z модулей за вычеты модулярного кода по системе попарно простых модулей из таблицы №2, находят избыточные вычеты u_j,n+1, …, u_j,n+r по правилу: , где по системе модулей из таблицы №2, далее определяют номера контейнеров, которым соответствуют избыточные вычеты и порядок их следования в модулярном коде {N_j,1, …, N_j,t}, объединяют полезную и служебную информации, формируя, тем самым, двоичные блоки , выполняют обратную сортировку блоков , восстанавливая порядок их следования в соответствии с естественным порядком следования контейнеров α_j,1, α_j,2, …, α_j,Z, и по ключу для стеганографического преобразования K_стег встраивают информационные блоки в Z контейнеров методами стеганографии, передают их в канал связи.