Способ сплайн-фильтрации сигналов

Способ сплайн-фильтрации сигналов

Иллюстрации

Показать все

Реферат

Настоящее изобретение относится к области радиоэлектроники, а именно к способам обработки и обнаружения сигнала на фоне помех. Задача, на решение которой направлено заявленное изобретение, заключается в реализации разработки оптимального метода обнаружения гидроакустического сигнала в условиях помех, описываемых нелинейными стохастическими уравнениями. Поставленная задача решается за счет того, что в заявленном способе нелинейная функция представляется через сплайны, что дает возможность проводить линейную обработку на каждом интервале и представлять нелинейный алгоритм как композицию линейного фильтра Калмана-Бьюси.

Достигаемый технический результат заключается в уменьшении вычислительных затрат, обеспечении высокой эффективности обнаружения и в универсальности обработки при различных помехах. Возможность работы в реальном масштабе времени, получение более эффективного алгоритма фильтрации, требующего меньше вычислительных затрат, обуславливают высокую экономическую выгоду, которая может быть использована при внедрении в систему обработки гидроакустических сигналов.

На сегодняшний день приближенные решения уравнений фильтрации основаны на аппроксимации решения - апостериорной плотности вероятности некоторой функцией из параметризованного класса, при этом используют нормальную плотность вероятности [1]. Однако в ряде случаев апостериорная плотность вероятности существенно отличается от нормальной (к примеру, процесс ближней реверберации) и при возникновении больших ошибок фильтрации (малое отношение сигнал-шум, помеха-шум) требуются более точные приближения. С этой точки зрения особенно привлекательными являются аппроксимации, основанные на сплайновых представлениях, так как при их применении никаких допущений по поводу законов распределений не делается.

Из предшествующих методик известен метод условной марковской фильтрации (прототип) (2, с. 213-222], в котором взаимосвязь сигнала и помехи выражается некоторой детерминированной функцией, а белый шум - аддитивен. Основная задача метода состоит в том, чтобы, располагая одним из компонентов многомерного марковского процесса, вычислить распределение вероятностей для значений наблюдаемого компонента, где сигнал является произвольной детерминированной функцией по времени S(x,t)=S(t), а помеха V(η,t)=η(t) представляется диффузионным гауссовским процессом. Суть работы метода условной марковской фильтрации можно выразить в системе уравнений:

где: s(t) - детерминированный сигнал; u(t) - поступающая входная реализация; z(t) - логарифм отношения правдоподобия; - оценка реверберационной помехи при гипотезе наличия сигнала; - оценка реверберационной помехи при гипотезе отсутствия сигнала; σ^*2 - дисперсия оценки помехи; N₀ - величина спектральной плотности белого шума; γ - коэффициент диффузии.

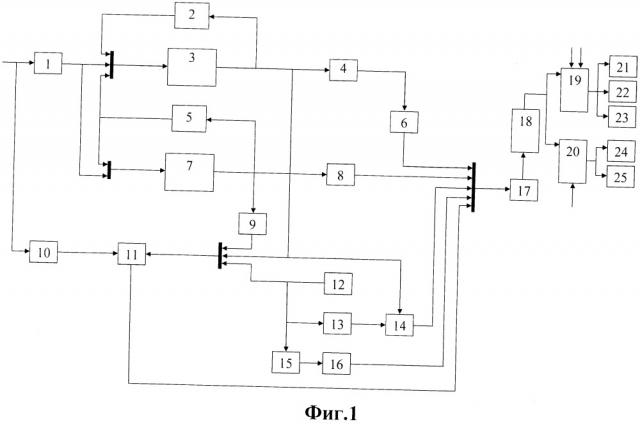
Схема, реализующая указанный метод условной марковской фильтрации (прототип) [2, с. 213-222], приведена на фиг. 1. где:

блок 1 - блок усиления на коэффициент ;

блок 2 - блок усиления на коэффициент ;

блоки 3, 7, 18 - интеграторы:

блок 5 - блок усиления на коэффициент ;

блоки 4, 8, 15 - квадраторы;

блоки 6, 9, 16 - блоки усиления на коэффициент [-1];

блоки 10, 13 - блоки усиления на коэффициент [2];

блоки 11, 14 - премножители;

блок 12 - блок формирования опорного сигнала;

блок 17 - блок усиления на коэффициент ;

блок 19 - двухпороговое устройство;

блок 20 - однопороговое устройство;

блоки 21, 24 - блоки принятия решения при гипотезе наличия сигнала;

блок 22 - блок принятия решения при гипотезе отсутствия сигнала;

блок 23 - блок, реализующий продолжение наблюдения.

Принцип действия метода заключается в следующем: при гипотезах наличия и отсутствия сигнала вычисляются оценочные значения отфильтрованной от белого шума помехи, на их основе формируют логарифм отношения правдоподобия и затем выносят решение в одной из двух пороговых схем. Метод условной марковской фильтрации позволяет получить структурные схемы оптимальных приемников для различных помеховых ситуаций, но не производит оценку помехоустойчивости таких приемников.

Также известен метод кусочного разложения оценок (патент №2257610), который основан на разбиении исходной дискретной реализации на прикрывающиеся интервалы одинаковой длины с последующей оценкой на каждом из них полезного сигнала (аналог) [3, с. 4-10]. Исходя из данного метода, предполагается, что полезный сигнал описывается некоторой кусочно-непрерывной гладкой функцией, которая удовлетворяет условиям теоремы Вейерштрассе об аппроксимации на локальных отрезках. Такой подход позволяет получить множество оценок полезной составляющей в каждом сечении процесса с последующим их усреднением. Использование системы ортогональных многочленов при решении задачи аппроксимации позволяет получить только общее решение задачи оценки сигнала и обрабатывать одномерные дискретные реализации сигналов ограниченного объема в условиях непараметрической априорной неопределенности, что делает метод сплайн-фильтрации по сравнению с методом кусочного разложения оценок более универсальным.

При переходе от аппроксимаций многочленами к аппроксимации сплайнами преследуют две цели. Первая - это улучшение качества приближения: при одинаковых вычислительных затратах абсолютные погрешности аппроксимации сплайнами меньше, чем абсолютные погрешности аппроксимации многочленами, а при одинаковых погрешностях уменьшается объем вычислений. Сплайны позволяют избежать осцилляций [4-6]. Для сходимости аппроксимации к аппроксимируемой функции предъявляются более слабые требования, чем в случае многочленов. Например, интерполяция сплайнами невысоких степеней сходится даже для непрерывных функций. Вторая цель - резкое уменьшение вычислительных трудностей как при построении алгоритмов решения задач, так и при дальнейшей работе с аппроксимантами, которые на каждом звене представляют собой многочлены невысоких степеней или иные элементарные функции [4,5].

Асимптотически наилучшее равномерное приближение сплайном первой степени S₁(x) функции ƒ(x) определяется выражением [7]:

где: x_i, x_i+1 - узловые точки на интервале; Δ_i - интервал с номером секции i. Сплайновое представление тестового сигнала, показано на фиг. 2. где:

x₁, x₂, x₃ - узловые точки на интервале;

Δ₁, Δ₂, Δ₃ - интервалы;

r(x) - тестовый сигнал, у которого коэффициент сноса равен r(x)=-0,5х²-x;

s(x) - сплайновое представление сигнала r(x).

В рамках данного изобретения для удовлетворения требования непрерывности плотности вероятности применялась операция сглаживания высокочастотных составляющих характеристической функции путем замены высокочастотных отсчетов нулями. Спектральные плотности вероятности тестового процесса ps(x) и его приближение сплайнами представлено на фиг. 3. где:

x - значения тестового процесса;

ps(x) - плотность вероятности тестового процесса;

phx(x)- плотность вероятности приближения тестового процесса сплайнами.

Обе кривые (фиг. 3) имеют схожую форму нормального распределения с положительными коэффициентами асимметрии: для плотности вероятности тестового сигнала он равен 0,77, а для плотности вероятности приближения тестового процесса сплайнами - 0,75; также оба распределения имеют только по одному возможному значению, соответствующему наибольшей вероятности появления, и являются одномодальными.

Аппроксимировать исходную функцию можно различными способами, но для решения задачи линейной фильтрации выражение (2) на интервалах [x_i, x_i+1) рассматривается как линейное стохастическое уравнение. Вследствие этого алгоритм фильтрации на интервале можно представить как фильтр Калмана с параметрами, меняющимися в зависимости от номера секции, к которой принадлежит текущая оценка процесса. Известно, что в задачах линейной фильтрации нет необходимости вычислять плотность вероятности, достаточно найти оценку математического ожидания процесса в каждой точке и дисперсию этой оценки [5-7]. Таким образом можно записать уравнение фильтрации случайного процесса x(t)∈Δ_i:

где: x^* - текущая оценка процесса; h - функция прямоугольного окна; a_i, b_i - коэффициенты, значения которых определяются через узловые точки x_i и значения функции ƒ(х_i) через систему уравнений:

Если рассматривать весь интервал изменения x∈X, то дисперсия фильтрации случайного процесса x(t) будет представляться вектором (, , …σ_n), при котором имеет место соответствие: , тогда система уравнений фильтрации представляется уравнениями:

Из выражения (5) следует, что в стационарном режиме дисперсия фильтрации постоянна на интервалах Δ_i и меняется при переходе к другому интервалу ступенчатым образом. При этом необходимо отметить, что на каждом интервале реализуется линейный фильтр Калмана-Бьюси. При этом дисперсия фильтрации является функцией только оценки . Важным фактором с вычислительной точки зрения является то, что стационарные коэффициенты усиления могут быть рассчитаны априори и могут представляться в виде набора чисел, поэтому реализация метода фильтрации со стационарными коэффициентами требует значительно меньших объемов памяти и вычислительных затрат [5].

Метод сплайн-фильтрации позволяет оценивать случайные процессы, заданные не только скалярным, но и матрично-векторным уравнением. Преимущества предлагаемого подхода в вычислительном отношении, по сравнению с известными методами нелинейной фильтрации, более существенны. В случае решения задачи обнаружения сигнала на фоне помехи и белого шума уравнения обнаружения и фильтрации имеют вид [4-7]:

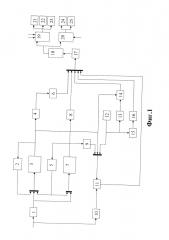
Предлагаемый способ сплайн-фильтрации на основе прототипа и системы уравнений (6) представлен на фиг. 4, где:

блок 14 - блок усиления на коэффициент ;

блок 7 - блок усиления на коэффициент ;

блоки 8, 12, 26 - интеграторы;

блок 10 - блок усиления на коэффициент ;

блоки 9, 13, 21 - квадраторы;

блоки 11, 15, 22 - блоки усиления на коэффициент [-1];

блоки 16, 19 - блоки усиления на коэффициент [2];

блоки 17, 20 - перемножители;

блок 18 - блок формирования опорного сигнала;

блок 25 - блок усиления на коэффициент ;

блок 27 - двухпороговое устройство;

блок 28 - однопороговое устройство;

блоки 29, 32 - блоки принятия решения при гипотезе наличия сигнала;

блок 30 - блок принятия решения при гипотезе отсутствия сигнала;

блок 31 - блок, реализующий продолжение наблюдения;

дополнительно включенные блоки:

блок 1 - блок определения узловых точек на интервале;

блок 2 - блок формирования системы интервалов;

блок 3 - блок сравнения оценки помехи с системой интервалов;

блок 4 - блок определения значения оценки помехи |x^*(1)];

блок 5 - блок определения величины коэффициента [a_i];

блок 6 - блок определения величины коэффициента [b_i];

блок 23 - блок вычисления значения следующей оценки помехи [х^*(2)];

блок 24 - блок вычисления значения следующей оценки помехи [х^*(3)].

Работает изобретение следующим образом: находится значение оценки помехи х^*(1). Значение оценки х^*(1) соотносится с системой {Δ_i}. В результате определяются величины коэффициентов а_i(1), b_i(1) и дисперсия , которые используются для определения следующей оценки x^*(2). С приходом отсчета реализации u₁ на основании системы уравнений [3] вычисляется следующая оценка помехи х^*(2). Полученное значение x^*(2) соотносится с множеством интервалов {Δ_i} и снова определяется тройка {a_i, b_i, }. С учетом полученных значений коэффициентов a_i(2), b_i(2), дисперсии и системы [3] находится следующее значение оценки помехи х^*(3). Процедуры определения коэффициентов для следующих оценок на основании системы уравнений повторяется. Получение оценок помехи при нелинейном уравнении состояния происходит при использовании сплайн-интерполяции нелинейной функции, где область динамического диапазона изменений нелинейной функции разбивается на интервалы, в каждом из которых реализуется линейное представление уравнения состояния, что позволяет на каждом из поддиапазонов реализовать фильтр Калмана-Бьюси. Фильтр включает в себя: два уравнения оценки состояния при гипотезах наличия/отсутствия сигнала; уравнения оценки дисперсии на различных интервалах и уравнения правдоподобия, включающего эти оценки, и по результатам вычисления которого выносится решение об обнаружении или необнаружении сигнала.

Метод сплайн-фильтрации основан на аппроксимации зависимости ƒ(x) сплайн-функцией S₁(x), что позволяет использовать линейный фильтр Калмана с коэффициентами, значения которых заранее рассчитываются. Значения a_i и b_i могут быть получены априори, исходя из вида зависимости ƒ(x) и необходимой точности аппроксимации, так как уравнение Риккати для коэффициента усиления фильтра Калмана не содержит измеряемых данных.

Имитационное моделирование способа сплайн-фильтрации производится в среде пакета MathCAD на основе системы уравнений (6). На первом этапе моделируются шумы формирования и наблюдения реализации белого гауссовского шума, после чего на основании исходного нелинейного динамического уравнения моделируется структурно связанная с сигналом помеха, которая представлена на фиг. 5, где:

i - число дискретных отсчетов;

j - число спектральных отсчетов;

n_i - помеха;

Fz_j - спектральная плотность входной реализации.

Описанным выше способом представлен тестовый сигнал и сформирована реализация входного случайного процесса, которые показаны на фиг. 6, где:

i - число дискретных отсчетов;

z_i - входная реализация;

St_i - тестовый сигнал.

Учитывая специфику реверберации, спектральные плотности помехи и сигнала выбираются одинаковыми, что показано на фиг. 7, где:

i, j - число спектральных отсчетов;

Fs_j - спектральная плотность тестового сигнала;

Fr_i - спектральная плотность помехи.

Непосредственное моделирование уравнений (5) производится при условиях, где коэффициент сноса в динамическом уравнении помехи определяется функцией r(x)=-0,05x²-0,3x, которая аппроксимируется кусочно-линейной функцией, представляющей собой два отрезка прямой, при котором входное отношение сигнал/помеха равно 0.5, а число дискретных отсчетов - 64. На фиг. 8 представлены кривые значений помехи и ее оценки, где:

i - число спектральных отсчетов;

n_i - помеха;

n^*_i - оценка помехи.

Рассматривая значения помехи и ее оценку (фиг. 8), в среде MathCAD была определена относительная ошибка способа сплайн-фильтрации, которая составила 0.05% и на основании которой можно констатировать, что метод сплайн-фильтрации позволяет достаточно эффективно решать задачи нелинейной фильтрации помехи и обнаружения сигналов путем представления исходного нелинейного алгоритма как композиции линейного фильтра Калмана-Бьюси.

Сравнительный анализ способа сплайн-фильтрации с прототипом и аналогом показал, что предлагаемый подход не уступает по такому показателю, как выходное отношение сигнал-помеха, причем различие сводится к минимуму, если увеличивается число аппроксимирующих отрезков. Способ сплайн-фильтрации дозволяет оценивать случайные процессы, заданные не только скалярным, но и матрично-векторным уравнением. Экстраполяция полученных результатов на этот случай не представляет трудностей, а преимущества предлагаемого подхода в вычислительном отношении, по сравнению с известными методами нелинейной фильтрации, становятся еще более существенными.

Список использованных источников

1. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М.: Радио и связь, 1991, 608 с.

2. Казаков В.А. Введение в теорию марковских процессов и некоторые радиотехнические задачи. М.: Советское радио, 1973. 232 с. (прототип, с. 213-222).

3. Марчук В.И., Шерстобитов А.И., Гавриленко Д.С. Особенности фильтрации цифровых сигналов в условиях ограниченности выборки его исходной реализации. Успехи современной радиоэлектроники. Зарубежная радиоэлектроника. 2011. №9. С. 4-10 (аналог, с. 4-10).

4. Бурова И.Г., Демьянович Ю.К. Теория минимальных сплайнов. - СПб: Издательство СПбГУ, 2001. - 315 с.

5. Завьялов Ю.С., Квасов Б.Н., Мирошниченко В.Л. Метод сплайн-функций. М.: Наука, 1980.

6. Розов А.К. Нелинейная фильтрация сигналов. - СПб.: Политехника, 1994. - 381 с.

7. Бутырский Е.Ю. Обнаружение сигналов на фоне марковской реверберационной помехи // Научное приборостроение. - 2012. - Т. 22. - №1. - С. 87-95.

Способ сплайн-фильтрации сигналов на основе метода условной марковской фильтрации, содержащей: операции решения уравнений фильтрации для гипотезы наличия/отсутствия сигнала; операции решения уравнения правдоподобия и уравнения для вычисления коэффициентов усиления, отличающийся тем, что для получения оценок помехи при нелинейном уравнении состояния и уменьшении вычислительных затрат при нелинейной фильтрации дополнительно используется операция сплайн-интерполяции нелинейной функции путем операции разбиения динамического диапазона изменений нелинейной функции на интервалы, в каждом из которых реализуется операция линейного представления уравнения состояния, что позволяет на каждом из поддиапазонов реализовать фильтр Калмана-Бьюси, включающего в себя: операции двух уравнений оценки состояния при гипотезах наличия/отсутствия сигнала; операции решения уравнения оценки дисперсии на различных интервалах и операции решения уравнения правдоподобия, включающего эти оценки, и по результатам вычисления которого выносится решение об обнаружении или необнаружении сигнала.