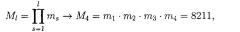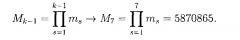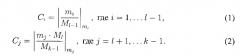Устройство вычисления модулярного произведения монтгомери

Устройство вычисления модулярного произведения монтгомери

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике, а именно к вычислительным модулярным системам, и предназначено для умножения двух чисел, представленных в системе остаточных классов (СОК, RNS).

Ряд алгоритмов шифрования основан на модулярной арифметике, например алгоритмы Диффи-Хелмана, Эль-Гамаля, RSA. Модулярная арифметика включает в себя множество модульных операций, таких как модулярное сложение, модулярное умножение, модулярное деление и т.д. Например, А ⋅ В mod р = Г является примером модулярного умножения.

Для задач криптографии размеры сомножителей А и В, представленных в двоичной форме, могут достигать более 1024 бит каждый, и, следовательно, результат умножения будет иметь размер более 2048 бит. Нахождение остатка от деления для такого числа является вычислительно сложной задачей.

Один из подходов к повышению эффективности выполнения модулярного умножения предложен в [Montgomery Modular multiplication without trial division // Mathematics of computation. - 1985. - T. 44. - №170. - C. 519-521.] Он заключается в замене нахождения результата по большому модулю p на операции по модулю R, который выбирается таким образом, чтобы операции деления и нахождения остатка были эффективными. Часто R берется в виде степени числа 2. Также должен выполняться ряд условий: R > p, R и p взаимно простые, а также вводятся R^-1 и p', удовлетворяющие выражениям 0 < R^-1 < p, 0 < p' < R и RR^-1 - pp' = 1. Последнее выражение является диафантовым уравнением и может быть решено, например, методом Евклида. Тогда алгоритм нахождения произведения Монтгомери можно описать алгоритмом 1.

Алгоритм 1: Произведение Монтгомери

Функция MontMult(A ⋅ В)

m ← (А ⋅ В mod R) p' mod R

t ← (А ⋅ В + m ⋅ p) / R

Если t≥p то

вернуть t - p

иначе

вернуть t

Использование данного алгоритма в вычислительных устройствах позволяет уменьшить аппаратную сложность. Однако недостатком этого подхода является то, что результатом алгоритма MontMult(A ⋅ В) является не точный результат А ⋅ В mod p, а масштабированный. Для перевода значения t в немасштабированный вид остатка по модулю p, необходимо вычислить t ⋅ R mod p или, что эквивалентно, применить алгоритм Однако представление Монтгомери является полноценным представлением чисел, допускающим выполнение операций над масштабированными значениями, поэтому перевод к немасштабированному виду необходим лишь в конце вычислений.

Одним из способов повышения производительности вычисления произведения Монтгомери является применение СОК. В СОК целое число представляется в виде остатков от деления на набор модулей, а арифметические операции над числами заменяются на операциями над остатками. Выполнение операций происходит параллельно без межразрядных переносов, что позволяет очень быстро реализовать сложение, вычитание и умножение.

Известен способ умножения Монтгомери в СОК (патент US 7027598, опубл. 11.04.2006). Согласно описанному выше алгоритму, способ сводится к выполнению сначала S = MontMult(A ⋅ Q), где Q=(R² mod p) - предвычисленная константа, а после F = MontMult(B ⋅ S), где F - конечный результат. В данном изобретении при использовании модулярной арифметики применяют два базиса V и W, все модули v_i и w_i, (i = 1, …, n), которых взаимно простые. Недостатком данного способа является необходимость три раза переводить результаты между базисами, что является вычислительно сложной операцией.

Наиболее близким к предлагаемому устройству, выбранным в качестве прототипа, является устройство для умножения чисел в модулярной системе счисления с плавающей запятой (авторское свидетельство SU №1411741, опубликован 23.07.1988), содержащее тактовый вход устройства, выход мантиссы результата устройства, вход мантиссы первого операнда устройства, вход мантиссы второго операнда устройства, вход порядка первого операнда устройства, вход порядка второго операнда устройства, выход порядка результата устройства, выход признака переполнения устройства, вычитатель порядка произведения, первый элемент задержки, схему сравнения с константой, блок модульных умножителей, блок масштабирования чисел, блок вычисления интервального индекса числа, блок суммирования вычетов сумматора порядков, вспомогательный регистр, второй элемент задержки.

Недостатком данного изобретения являются ограниченные функциональные возможности и большая аппаратная сложность.

Техническим результатом заявляемого изобретения является расширение функциональных возможностей и снижение аппаратной сложности за счет применения в устройстве модифицированного метода Монтгомери для вычисления произведения чисел, представленных в СОК.

Данный технический результат достигается тем, что в устройство вычисления модулярного произведения Монтгомери, содержащее вход первого операнда, вход второго операнда, блок умножителей по модулю, блок вычисления первой интервально-индексной характеристики, блок сравнения с константой, где вход первого операнда подключен к первому входу блока умножителей по модулю, ко второму входу которого подключен вход второго операнда введены вход модуля, регистр хранения модуля, блок хранения параметра F, блок вычисления параметра D по первому базису, блок хранения значений R_i,l, где i=1, …, l, l - количество модулей в первом базисе, блок хранения значений R_i,j, здесь i=1, …, l-1, j = l+1, …, k, k - количество модулей в двух базисах, блок вычисления параметра D по второму базису, блок вычисления произведения Монтгомери по второму базису, блок хранения значений R_j,k, блок хранения значений R_j,i, здесь j=l+1, …, k-1, блок вычисления второй интервально-индексной характеристики, блок корректировки второй интервально-индексной характеристики, мультиплексор, блок вычисления произведения Монтгомери по первому базису, регистр хранения произведения Монтгомери, выход произведения Монтгомери, где первый выход блока умножителей по модулю соединен с первым входом блока вычисления параметра D по первому базису, второй вход которого соединен с выходом блока хранения параметра F, на вход которого с первого выхода регистра хранения модуля поступают значения модуля по первому базису, вход регистра хранения модуля подключен ко входу модуля, а со второго выхода регистра хранения модуля значения модуля по второму базису поступают на третий вход блока вычисления произведения Монтгомери по второму базису, второй вход которого подключен к выходу блока вычисления параметра D по второму базису, второй вход которого соединен с выходом блока вычисления первой интервально-индексной характеристики, вход которого подключен к выходу блока хранения значений R_i,l, вход которого подключен к выходу блока вычисления параметра D по первому базису, который также соединен со входом блока хранения значений R_i,j, выход которого соединен с первым входом блока вычисления параметра D по второму базису, второй выход блока умножителей по модулю соединен с первым входом блока вычисления произведения Монтгомери по второму базису, выход которого одновременно подключен ко входу блока хранения значений R_j,k, ко входу блока хранения значений R_j,i, к первому входу регистра хранения произведения Монтгомери, второй вход которого соединен с выходом блока вычисления произведения Монтгомери по первому базису, первый вход которого соединен с выходом блока хранения значений R_j,i, а второй вход подключен к выходу мультиплексора, управляющий вход которого подключен к выходу блока сравнения с константой, вход которого подключен ко входу блока корректировки второй интервально-индексной характеристики, к выходу блока вычисления второй интервально-индексной характеристики и к первому входу мультиплексора, второй вход которого соединен с выходом блока корректировки второй интервально-индексной характеристики, выход блока хранения значений R_j,k подключен ко входу блока вычисления второй интервально-индексной характеристики, выход регистра хранения произведения Монтгомери соединен с выходом произведения Монтгомери.

Данное устройство вычисления модулярного произведения Монтгомери поясняется фигурой 1, на которой представлен общий вид устройства вычисления модулярного произведения Монтгомери, содержащего вход первого операнда 1, вход второго операнда 2, блок умножителей по модулю 3, вход модуля 4, регистр хранения модуля 5, блок хранения параметра F 6, блок вычисления параметра D по первому базису 7, блок хранения значений R_i,l 8, блок хранения значений R_i,j 9, блок вычисления первой интервально-индексной характеристики 10, блок вычисления параметра D по второму базису 11, блок вычисления произведения Монтгомери по второму базису 12, блок хранения значений R_j,k 13, блок хранения значений R_j,i 14, блок вычисления второй интервально-индексной характеристики 15, блок корректировки второй интервально-индексной характеристики 16, блок сравнения с константой 17, мультиплексор 18, блок вычисления произведения Монтгомери по первому базису 19, регистр хранения произведения Монтгомери 20, выход произведения Монтгомери 21.

Сущность изобретения основана на следующем математическом аппарате. Определяют два базиса СОК М₁ и M₂ с взаимно простыми модулями m_i и количеством модулей в первом базисе и k = 8 всего модулей в обоих базисах, т.е. во втором базисе модуля.

Тогда объединенный базис

Затем вычисляют вспомогательный модуль то, удовлетворяющий соотношению т.е. Подставляя данные значения, получают, что Возьмем m₀ = 8.

Вычисляют необходимые для работы константы.

Затем вычисляют следующие остатки:

и следующие величины

где - мультипликативная инверсия числа m по модулю p.

Для работы также необходимо определить значение следующих констант:

По формулам (1)-(2) вычисляют константы:

Затем находят все необходимые константы:

По формулам (3)-(4) находят следующие значения:

По формуле (5) определяют:

По формулам (6)-(7):

По формуле (8) находят:

Затем задают модуль p, удовлетворяющий условию

В качестве примера значение модуля берется равным

Из значения модуля p по первому базису M₁ вычисляют параметр

В качестве сомножителей берут два операнда, представленных в СОК:

где A, В < p, и находят значение

Затем находят по первому базису параметр

Из полученных значений C_i,j, C_i, D по формулам

вычисляют следующие значения:

Затем по формуле

находят первую интервально-индексную характеристику

По формуле

вычисляют значения R_i,j:

По формуле

находят значение параметра D по второму базису:

По формуле

находят результат вычисления произведения Монтгомери по второму базису М₂:

По формулам

вычисляют значения:

Затем по формуле

вычисляют вторую интервально-индексную характеристику

Затем вторую интервально-индексную характеристику сравнивают с константой m₀. Значение второй интервально-индексной характеристики корректируют на основе выражения:

Из выражения (18), проверяя условие и т.к. 0 < 8, скорректированную вторую интервально-индексную характеристику принимают равной

Далее по формуле

находят следующие значения:

И, наконец, из выражения

находят результат вычисления произведения Монтгомери по первому базису

Таким образом, получено значение произведения Монтгомери в СОК.

Обратим внимание, что полученное значение является масштабированным и для получения немасштабированного значения нужно выполнить данный алгоритм еще раз со значениями:

и

Результатом работы алгоритма является число в СОК: (0, 2, 4, 3, 2, 6, 7, 15).

Проверим данное значение:

Таким образом, алгоритм работает верно.

Опишем работу устройства на основе данного алгоритма.

На входы первого операнда 1 и второго операнда 2 подаются соответственно значения сомножителей А и В, представленные в СОК, которые поступают на блок умножителей по модулю 3, где вычисляется значение Значения С по первому базису с первого выхода блока умножителей по модулю 3 поступают на первый вход блока вычисления параметра D по первому базису 7, значения С по второму базису со второго выхода блока умножителей по модулю 3 поступают на первый вход блока вычисления произведения Монтгомери по второму базису 12.

Значение модуля p поступает на вход модуля 4, откуда оно записывается в регистр хранения модуля 5. Значения модуля p по первому базису поступают на вход блока хранения параметра F 6, который реализован в виде ПЗУ, на вход которого подается число а на выход поступает параметр Реализация табличным способом в виде ПЗУ позволит избежать вычислительно сложной операции нахождения мультипликативной инверсии. С выхода блока хранения параметра F 6 значение F поступает на второй вход блока вычисления параметра D по первому базису 7, где вычисляется

Значение параметра D с выхода блока вычисления параметра D по первому базису 7 одновременно поступает на вход блока хранения значений 8 и вход блока хранения значений R_i,j 9.

В блоке хранения значений 8 на основе значений табличным способом получают хранящиеся там значения вычисленные по формулам (9)-(10), которые поступают на вход блока вычисления первой интервально-индексной характеристики 10 которая вычисляется по формуле (11). Затем значение первой интервально-индексной характеристики с выхода блока вычисления первой интервально-индексной характеристики 10 поступает на второй вход блока вычисления параметра D по второму базису 11.

В блоке хранения значений R_i,j 9 на основе значений табличным способом получают хранящиеся там значения вычисленные по формуле (12), которые поступают на первый вход блока вычисления параметра D по второму базису 11.

В блоке вычисления параметра D по второму базису 11 по формуле (13) происходит вычисление значений , которые поступают на второй вход блока вычисления произведения Монтгомери по второму базису 12, на третий вход которого со второго выхода регистра хранения модуля 5 поступают значения модуля p по второму базису:

В блоке вычисления произведения Монтгомери по второму базису 12 по формуле (14) находят результат вычисления произведения Монтгомери по второму базису который поступает одновременно на первый вход регистра хранения произведения Монтгомери 20, на вход блока хранения значений R_j,i 14 и на вход блока хранения значений R_j,k 13.

В блоке хранения значений R_j,k 13 на основе значений табличным способом получают хранящиеся там значения R_j,k, вычисленные по формулам (15)-(16), которые поступают на вход блока вычисления второй интервально-индексной характеристики 15 В блоке вычисления второй интервально-индексной характеристики 15 по формуле (17) происходит вычисление значение которой одновременно поступает на первый вход мультиплексора 18, на вход блока корректировки второй интервально-индексной характеристики 16 на вход блока сравнения с константой 17.

В блоке корректировки второй интервально-индексной характеристики 16 по формуле (18) вычисляют которое поступает на второй вход мультиплексора 18.

В блоке сравнения с константой 17 проверяется условие результат которого поступает на управляющий вход мультиплексора 18. На выход мультиплексора 18 поступает значение скорректированное на основе выражения (18), которое затем поступает на второй вход блока вычисления произведения Монтгомери по первому базису 19.

В блоке хранения значений R_j,i 14 по формуле (19) происходит вычисление значений которые поступают на первый вход блока вычисления произведения Монтгомери по первому базису 19.

В блоке вычисления произведения Монтгомери по первому базису 19 по формуле (20) вычисляют значения произведения Монтгомери по первому базису которые поступают на второй вход регистра хранения произведения Монтгомери 20.

На выход регистра хранения произведения Монтгомери 20 поступает значение произведение Монтгомери по обоим базисам.

Устройство вычисления модулярного произведения Монтгомери, содержащее вход первого операнда, вход второго операнда, блок умножителей по модулю, блок вычисления первой интервально-индексной характеристики, блок сравнения с константой, где вход первого операнда подключен к первому входу блока умножителей по модулю, ко второму входу которого подключен вход второго операнда, отличающееся тем, что в него введены вход модуля, регистр хранения модуля, блок хранения параметра F, блок вычисления параметра D по первому базису, блок хранения значений R_i,l, где i=1, …, l, l - количество модулей в первом базисе, блок хранения значений R_i,j, здесь i=1, …, l-1, j=l+1, …, k, k - количество модулей в двух базисах, блок вычисления параметра D по второму базису, блок вычисления произведения Монтгомери по второму базису, блок хранения значений R_j,k, блок хранения значений R_j,i, здесь j=l+1, …, k-1, блок вычисления второй интервально-индексной характеристики, блок корректировки второй интервально-индексной характеристики, мультиплексор, блок вычисления произведения Монтгомери по первому базису, регистр хранения произведения Монтгомери, выход произведения Монтгомери, где первый выход блока умножителей по модулю соединен с первым входом блока вычисления D по первому базису, второй вход которого соединен с выходом блока хранения параметра F, на вход которого с первого выхода регистра хранения модуля поступают значения модуля по первому базису, вход регистра хранения модуля подключен ко входу модуля, а со второго выхода регистра хранения модуля значения модуля по второму базису поступают на третий вход блока вычисления произведения Монтгомери по второму базису, второй вход которого подключен к выходу блока вычисления параметра D по второму базису, второй вход которого соединен с выходом блока вычисления первой интервально-индексной характеристики, вход которого подключен к выходу блока хранения значений R_i,l, вход которого подключен к выходу блока вычисления параметра D по первому базису, который также соединен со входом блока хранения значений R_i,j, выход которого соединен с первым входом блока вычисления параметра D по второму базису, второй выход блока умножителей по модулю соединен с первым входом блока вычисления произведения Монтгомери по второму базису, выход которого одновременно подключен ко входу блока хранения значений R_j,k, ко входу блока хранения значений R_j,i, к первому входу регистра хранения произведения Монтгомери, второй вход которого соединен с выходом блока вычисления произведения Монтгомери по первому базису, первый вход которого соединен с выходом блока хранения значений R_j,i, а второй вход подключен к выходу мультиплексора, управляющий вход которого подключен к выходу блока сравнения с константой, вход которого подключен ко входу блока корректировки второй интервально-индексной характеристики, к выходу блока вычисления второй интервально-индексной характеристики и к первому входу мультиплексора, второй вход которого соединен с выходом блока корректировки второй интервально-индексной характеристики, выход блока хранения значений R_j,k подключен ко входу блока вычисления второй интервально-индексной характеристики, выход регистра хранения произведения Монтгомери соединен с выходом произведения Монтгомери.