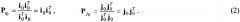Способ восстановления формы трёхмерного объекта по его двухмерным изображениям

Способ восстановления формы трёхмерного объекта по его двухмерным изображениям

Иллюстрации

Показать все

Реферат

Изобретение относится к области фотограмметрии и может быть использовано для восстановления формы трехмерного объекта и его пространственного положения по двухмерным изображениям этого объекта в разных ракурсах.

Известен способ (аналог) определения формы трехмерного объекта по его двухмерным изображениям, которые получают с использованием структурированного освещения [1]. В качестве структурированной подсветки используют паттерны, например, в виде черных и белых полос. В этом способе проектор и камера, регистрирующая изображение, разнесены в пространстве и для точек изображения объекта решается задача триангуляции, что позволяет построить карту глубин - зависимость расстояний до поверхности объекта от координат пикселов на изображениях. Полученная информация позволяет оценить форму объекта.

Этот способ имеет следующие недостатки.

1) Для его реализации необходимо специальное оборудование, обеспечивающее создание структурированного освещения.

2) Реализация этого способа сопряжена с дополнительным энергопотреблением, необходимым для работы устройств, обеспечивающих структурированное освещение.

3) Способ со структурированной подсветкой является активным, что в ряде случаев нежелательно в интересах скрытности наблюдения за объектом.

4) Способ этот может оказаться нереализуемым в принципе при наблюдении за удаленными объектами из-за невозможности осветить объект на большом расстоянии структурированным светом.

5) Проблематична реализация способа в условиях естественного дневного освещения, когда паттерны могут оказаться невидимыми.

6) Информация о форме объекта получается опосредованной, в виде карты глубин, что требует последующей обработки для удобного представления формы объекта.

От указанных недостатков свободен способ (прототип) [2] восстановления формы трехмерного объекта на основе стереоизображений, который заключается в том, что регистрируют изображения объекта в разных ракурсах, находят на изображениях соответственные точки, вычисляют известными методами их трехмерные координаты, применяют триангуляцию для получения формы объекта.

Преимущества прототипа по сравнению с аналогом следующие.

1) Упрощение аппаратуры и экономия энергопотребления ввиду отсутствия подсветки.

2) Обеспечение скрытности наблюдения за объектом.

3) Получение результата в наглядной форме.

4) Работоспособность на больших расстояниях и в условиях естественного освещения.

Недостатки прототипа следующие.

1) Неработоспособность при условии однородности поверхности объекта, при которой изображение объекта получится однородным и выявить соответственные точки будет невозможно.

2) Высокие требования к качеству изображений, которые должны обеспечивать возможность выявления соответственных точек по изображению объекта.

3) Большие вычислительные затраты, необходимые для выявления соответственных точек и решения задачи триангуляции.

Технической задачей данного изобретения является расширение области применения способа восстановления формы трехмерного объекта на объекты с однородной структурой, снижение требований к качеству регистрируемых изображений, сокращение вычислительных затрат за счет того, что форма объекта восстанавливается без выявления соответственных точек на изображениях и без триангуляции, снижение требований к взаимному положению систем регистрации изображений вследствие отсутствия необходимости получения перекрывающихся изображений, что необходимо для определения соответственных точек.

Поставленная задача достигается тем, что в способе восстановления формы трехмерного объекта по его двухмерным изображениям, заключающемся в регистрации под разными ракурсами двухмерных изображений объекта и восстановлении по этим изображениям трехмерной формы объекта, согласно изобретению контролируемую область пространства, в которой находится объект, разбивают на малые объемы - элементы разрешения (ЭР), нумеруют их и фиксируют их пространственные координаты, на каждом зарегистрированном изображении выделяют область, занятую непосредственно изображением объекта - область изображения объекта, расчетным путем определяют положения всех ЭР на плоскостях зарегистрированных изображений, для каждого зарегистрированного изображения выделяют номера тех ЭР, изображения которых попали в область изображения объекта, выбирают те номера ЭР, которые оказались выделенными одновременно для всех зарегистрированных изображений, восстанавливают форму трехмерного объекта как совокупность ЭР с выбранными номерами.

Особенностью и главным преимуществом заявляемого способа является возможность вообще не находить на изображениях соответственные точки. Вместо этого выявляются номера ЭР, составляющих тело объекта. Для этого достаточно иметь информацию только об области изображения объекта на каждом зарегистрированном изображении. Таким образом, снимаются требования как к неоднородности объекта, так и к качеству его изображений и к положению систем регистрации изображений. Фактически, достаточно знать области, занятые изображениями объекта на плоскостях зарегистрированных изображений.

Обоснование способа.

Решаемой задачей является восстановление формы наблюдаемого объекта и его пространственного положения по двухмерным изображениям объекта, полученным в разных ракурсах. Будем полагать, что известна контролируемая область пространства, в которой находится объект.

Разобьем контролируемую область пространства на малые объемы - элементы разрешения (ЭР), пронумеруем их и зафиксируем их пространственные координаты. Обозначим пространственные координаты ЭР трехмерными координатными векторами ρ₁, ρ₂, …, ρ_N, где N - число ЭР в контролируемой области пространства.

Часть ЭР попадает в тело объекта; назовем эти ЭР элементами разрешения объекта (ЭРО). Очевидно, что совокупность всех ЭРО составляет форму объекта и определяет его положение в пространстве. Если каким-либо образом определить все ЭРО, например их номера, то тем самым мы определим форму и пространственное положение объекта. Задача состоит, таким образом, в определении номеров всех ЭР, которые являются ЭРО, по зарегистрированным изображениям.

Будем полагать, что имеется М зарегистрированных изображений, на которых отображается контролируемая область пространства (необязательно полностью) в различающихся ракурсах. На каждом зарегистрированном изображении выделим область, занятую непосредственно изображением объекта - область изображения объекта.

Изображение объекта представляет собой распределение интенсивности по области изображения объекта. На каждом изображении распределение интенсивности по области изображения объекта определяется различными факторами, такими, например, как ракурс объекта и направление падающего на него света. Существующие способы определения формы объекта основаны на анализе изображения объекта, то есть на анализе распределения интенсивности по области его изображения. Это заставляет учитывать множество факторов, например видимость той или иной особой точки объекта в видимом ракурсе данного изображения (она может оказаться заслоненной, закрытой другой частью объекта). Это делает задачу анализа изображений трудоемкой и подверженной ощутимому влиянию различных факторов. Кроме того, для реализации способа-прототипа требуется специально организованное взаимное расположение систем регистрации изображений, с малой базой стереоскопичности, чтобы особые или просто выделяющиеся каким-то образом точки объекта оказались на всех изображениях для возможности их идентификации.

В заявляемом способе распределение интенсивности по области изображения объекта исключается из рассмотрения и на результат не влияет. Опираться будем только на саму область изображения объекта.

Очевидно, что, независимо от видимого ракурса изображения, область изображения объекта представляет собой совокупность изображений всех ЭРО. Не все ЭРО будут «видны» на том или ином конкретном изображении, некоторые из них будут накладываться одно на другое, что соответствует заслонению более удаленной части объекта на изображении передней его частью в данном видимом ракурсе. Однако геометрически именно совокупность всех ЭРО составит область изображения объекта. На каждом изображении, помимо ЭРО, в область изображения объекта могут попадать и те ЭР, которые не являются ЭРО. Однако на изображениях в разных ракурсах в область изображения объекта будут попадать разные ЭР, не являющиеся ЭРО и обязательно все ЭРО. На этом факте основано решение задачи выделения тех ЭР, которые являются ЭРО и составляют форму объекта.

Решается задача следующим образом.

Расчетным путем определим положения всех ЭР на плоскостях зарегистрированных изображений. Сделаем это методом проецирования на плоскости изображений координатных векторов ЭР. Используем ортогональное проецирование, полагая объект удаленным от систем регистрации изображений.

Пусть известно, что плоскость изображения перпендикулярна заданному вектору R. Найдем оператор проецирования на эту плоскость.

Согласно [3] оператор проецирования на вектор R определяется выражением а оператор проецирования на ортогональную вектору R плоскость (плоскость изображения) - оператором

Найдем базисные орты плоскости изображения. Будем полагать, что направление базисного орта оси ординат плоскости изображения j₀ определяется проекцией базисного орта j базовой системы координат на плоскость изображения, а базисный орт оси абсцисс плоскости изображения i₀ составляет с векторами j₀ и R правую систему координат. Это значит, что где оператор Q определяется выражением (1), [j₀R] - векторное произведение, - модуль вектора.

Чтобы определить положения всех ЭР на плоскости изображения, необходимо найти проекции их координатных векторов ρ₁, ρ₂, …, ρ_N на оси координат, задаваемые ортами i₀, j₀. Проецирующие на эти оси операторы определяются выражениями

В выражениях (2) учтены равенства

Таким образом, проекционный оператор на плоскость изображения равен а проекция вектора ρ_i на эту плоскость определяется выражением

в котором вектор ρ_i - трехмерный вектор пространственных координат i-го ЭР, ρ_i0 - двухмерный вектор координат проекции ρ_i на плоскость изображения, k_i - масштабирующий коэффициент, определяемый параметрами системы формирования изображения и дальностью ЭР. Масштабирующие коэффициенты могут быть рассчитаны для известных ЭР и параметров системы регистрации изображения.

Подставляя в (3) координатные векторы всех ЭР, получим все их проекции на плоскость изображения. Очевидно, что при проецировании не все ЭР займут отдельный участок плоскости изображения: во многих случаях они будут накладываться, попадая на плоскости изображения в одно и то же место. Часть ЭР попадет в область изображения объекта. В отсутствие искажающих факторов (которые не учитываем) в область изображения объекта попадут все ЭРО и могут попасть ЭР, не являющиеся ЭРО. Для каждого зарегистрированного изображения выделим номера тех ЭР, изображения которых попали в область изображения объекта. Для каждого изображения это будут номера всех ЭРО и, вероятно, номера «лишних» ЭР контролируемой области пространства, наложившиеся на область изображения объекта. Но на каждом изображении номера этих «наложившихся» ЭР будут различаться, так как «наложившиеся» ЭР зависят от видимого ракурса объекта.

Остается отделить номера ЭРО от «наложившихся» ЭР, не являющихся ЭРО. Для этого используем все изображения. Выберем те номера ЭР, которые оказались выделенными одновременно для всех зарегистрированных изображений. Это будут номера тех ЭР, которые попали в область изображения объекта на всех изображениях. После этого восстанавливаем форму трехмерного объекта как совокупность ЭР с выбранными номерами.

Таким образом, форма объекта получается в виде совокупности всех ЭР, выделенных выше описанным образом. Чем больше будет проанализировано изображений в разных ракурсах, тем больше отсеется лишних, «наложившихся» ЭР, не являющихся ЭРО, а ЭРО останутся. И тем точнее восстановится форма объекта.

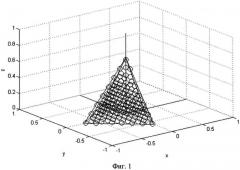
На фиг. 1-4 приведены результаты компьютерного моделирования применения заявляемого способа. На фиг. 1 показан трехмерный объект - пирамида и составляющие ее ЭРО, они показаны кружками. На фиг. 2 и 3 показаны два изображения, положения которых определяются, соответственно, векторами R₁=[1 1 1]^T и R₂=[-1 -1 1]^T. На этих изображениях кружками показаны изображения ЭР, попавшие в область изображения объекта. На фиг. 4 показана восстановленная форма объекта по этим двум изображениям, которая представляется совокупностью тех ЭР, которые попали в область изображения объекта на обоих изображениях. Как явствует из сравнения фиг. 1 и фиг. 4, восстановленная форма включает лишние ЭР, но несмотря на это, форма объекта достаточно достоверно отображается уже по двум изображениям. При увеличении числа зарегистрированных двухмерных изображений число лишних ЭР будет уменьшаться.

Преимущества предлагаемого способа по сравнению с прототипом следующие.

1) Определение формы объекта по двухмерным изображениям без нахождения соответственных точек на изображениях, что снимает целый ряд проблем.

2) Расширение класса анализируемых объектов на объекты с однородной структурой, для которых невозможно определить соответственные точки в пассивном режиме.

3) Снижение требований к качеству регистрируемых изображений. Это преимущество достигается за счет того, что распределение интенсивности в области изображения объекта в заявляемом способе не учитывается, соответственно и качество формирования этого распределения, то есть качество изображения, становится не важным, не влияющим на результат.

4) Отсутствие требований к взаимному расположению систем регистрации изображений. Это преимущество достигается за счет того, что, в отсутствие необходимости выявлять соответственные точки, изображения могут регистрироваться таким образом, что перекрывающихся областей изображения сцены вообще не будет, не будет соответственных точек на изображениях: можно, например, использовать изображения объекта, полученные с разных его сторон; на таких изображениях соответственных точек в принципе может не быть, но заявляемый способ позволяет по таким изображениям определить форму объекта, в отличие от прототипа.

5) Повышение информативности. Это преимущество достигается за счет возможности использовать изображения объекта, зарегистрированные в существенно различающихся ракурсах, в то время как в прототипе используются стереоизображения с малой базой, иначе невозможно найти соответственные точки. Таким образом, заявляемый способ позволяет получить форму объекта, наиболее приближенную к действительной, в то время как прототип позволяет выявить форму объекта только «с одной стороны».

6) Снижение вычислительных затрат. Это преимущество достигается за счет отсутствия в заявляемом способе таких емких в вычислительном плане процедур как нахождение соответственных точек и решение задач триангуляции.

Источники информации

1) Щекин С.Б. Восстановление формы трехмерных объектов методами структурированного освещения // Научно-технический вестник информационных технологий, механики и оптики, №43, 2007, стр. 301-307 (аналог).

2) Тупицын И.В. Реконструкция трехмерной модели объекта на основе стереопары при решении задач 3D моделирования // Вестник Сибирского государственного аэрокосмического университета имени академика М.Ф. Решетнева, №3 (36), 2011, стр. 88-92 (прототип).

3) Самойленко В.И., Пузырев В.А., Грубрин И.В. Техническая кибернетика: Учеб. пособие. - М.: Изд-во МАИ, 1994. - 280 с., стр. 271-272.

Способ восстановления формы трехмерного объекта по его двухмерным изображениям,

заключающийся в том, что регистрируют под разными ракурсами двухмерные изображения объекта и по этим зарегистрированным изображениям восстанавливают трехмерную форму объекта,

отличающийся тем, что контролируемую область пространства, в которой находится объект, разбивают на малые объемы - элементы разрешения (ЭР), нумеруют их и фиксируют их пространственные координаты, на каждом зарегистрированном изображении выделяют область, занятую непосредственно изображением объекта - область изображения объекта, расчетным путем определяют положения всех ЭР на плоскостях зарегистрированных изображений, для каждого зарегистрированного изображения выделяют номера тех ЭР, изображения которых попали в область изображения объекта, выбирают те номера ЭР, которые оказались выделенными одновременно для всех зарегистрированных изображений, восстанавливают форму трехмерного объекта как совокупность ЭР с выбранными номерами.