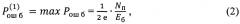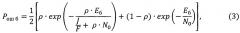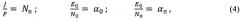Способ определения оптимальных значений показателей устойчивости системы связи с широкополосными сигналами к одновременному воздействию непрерывной и импульсной помех

Способ определения оптимальных значений показателей устойчивости системы связи с широкополосными сигналами к одновременному воздействию непрерывной и импульсной помех

Иллюстрации

Показать все

Реферат

Предлагаемое изобретение относится к области радиосвязи и может найти применение в телекоммуникационных радиоэлектронных системах с широкополосными сигналами.

В системах передачи дискретных сообщений предпочтительным показателем помехоустойчивости системы является средняя вероятность ошибки на бит информации. Поэтому предположим, что стратегия постановщика помех противника базируется на реализации такого распределения помехи по полосе частот F, занимаемой спектром сигналов с псевдослучайной перестройкой рабочей частоты (ППРЧ), которое при фиксированной средней мощности помехи обеспечивает максимум вероятности ошибки. При этом наиболее эффективным признается такое распределение, когда помеха поражает только часть общей полосы частот [Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи: базовые методы и характеристики: учеб. пособие. - М.: Эко-Трендз, 2005. С. 229-230].

Известен способ оценки части полосы частот, пораженной преднамеренной помехой, в системах радиосвязи (СРС) с ППРЧ и частотной модуляцией [Помехозащищенность систем радиосвязи с расширением спектра сигналов методом псевдослучайной перестройки рабочей частоты / В.И. Борисов, В.М. Зинчук, А.Е. Лимарев и др. - М.: Радио и связь, 2000. С. 73-74, формула (2.38)]. Способ обеспечивает выявление наихудшей для СРС (оптимальной для противника) помехи, при которой вероятность ошибки на бит максимальна. К недостаткам способа следует отнести отсутствие учета внутреннего шума приемной аппаратуры, поскольку его действием просто пренебрегают. Кроме того, при оценке помехоустойчивости систем связи достаточно широко распространен энергетический подход, предполагающий определение отношения сигнал/помеха, требуемого для обеспечения заданной вероятности ошибки, а рассмотренный способ не позволяет его реализовать с учетом внутреннего шума приемной аппаратуры.

Наиболее близким по технической сущности и совокупности существенных признаков к заявляемому способу является способ оценки части полосы частот, пораженной преднамеренной помехой, при некогерентном приеме сигналов с относительной фазовой модуляцией (ОФМ) и ППРЧ [Биленко А.П., Волков Л.Н. Сравнение помехозащищенности радиолиний с широкополосными сигналами // Радиотехника. - 1986. - №4. - С. 19, формулы (4), (5); Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи: базовые методы и характеристики: учеб. пособие. - М.: Эко-Трендз, 2005. С. 229-230], который и выбран в качестве прототипа. При этом способе оптимальное значение части () поражаемой преднамеренной помехой полосы частот, максимизирующее вероятность ошибки на бит, рассчитывают как отношение спектральной плотности помехи (N_п) к энергии принимаемого сигнала (Е_б), приходящейся на один бит

а максимальное значение вероятности ошибки на бит

где е - основание натурального логарифма (е≈2,718).

К недостаткам прототипа, как и ранее рассмотренного способа, следует отнести отсутствие учета внутреннего шума приемной аппаратуры и невозможность реализации энергетического подхода к оценке помехоустойчивости системы с его учетом.

На каналы систем радиосвязи с расширением спектра возможно одновременное воздействие помехи (шума), имеющей непрерывный характер, и помехи, имеющей прерывистый (импульсный) характер. Для систем радиосвязи с расширением спектра методом ППРЧ импульсный характер имеет помеха в части полосы частот, занимаемой спектром сигналов. Поэтому целью предлагаемого изобретения является определение оптимальных значений показателей устойчивости СРС к совместному действию импульсной и слабой непрерывной помех.

Известно, что при помехе в виде суммы белого гауссовского шума и преднамеренной помехи, поражающей только часть всей рабочей полосы частот, вероятность ошибки на бит при некогерентном приеме сигналов с относительной фазовой модуляцией описывается выражением [Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи: базовые методы и характеристики: учеб. пособие. - М.: Эко-Трендз, 2005. С. 229, формула (7.27)]

где ρ - часть всей рабочей полосы частот, пораженная преднамеренной помехой (0≤ρ≤1);

Е_б - энергия принимаемого сигнала, приходящаяся на один бит;

J - мощность преднамеренной помехи;

F - полоса частот, занимаемая спектром сигналов с ППРЧ;

N₀ - спектральная плотность непрерывной помехи (шума).

Для упрощения дальнейших преобразований введем обозначения

с учетом которых выражение (3) принимает вид

Рассмотрим случай действия импульсной помехи на фоне слабой непрерывной помехи (α₀≥10), при которой входящее в (5) значение (1-ρ)⋅ехр(-α₀)≤ехр(-10)=4,54⋅10^-5 достаточно мало, что позволяет записать приближенное равенство

В отличие от реализуемого прототипом подхода будем полагать, что при действии совместно с непрерывной помехой наилучшей для противника (наихудшей для СРС) импульсной помехой будет такая, которая перекрывает оптимальную часть рабочей полосы частот и обеспечивает максимальное требуемое отношение сигнал/импульсная помеха (α_{п max}) при заданной вероятности ошибки Р_{ош б}=Р_{ош зад}. Поэтому из (6) последовательными преобразованиями получим выражение для параметра α_п

;

;

;

;

Для поиска воспользуемся выражением (7), учитывающим оба вида помех. В соответствии с правилом отыскания экстремума функции найдем частную производную от функции (7) по параметру ρ и приравняем ее нулю

Из выражения (8) следует

Обозначим , откуда ;

После несложных преобразований (9) с учетом (10) получаем квадратное уравнение

х²+α₀⋅х+α₀=0,

решение которого имеет вид

Убедимся в работоспособности полученных соотношений (11), (10), подставив в них граничное значение параметра α₀=10 и Р_{ош зад}=10^-2,

;

х₁=-5+3,873=-1,127;

х₂=-5-3,873=-8,873;

;

.

Поскольку значение параметра ρ не может быть больше единицы, то из двух корней (11) выберем больший (x=x₁), то есть .

Таким образом, при предлагаемом способе оптимальное значение параметра ρ с учетом действия непрерывной помехи рассчитывается по формуле

а в соответствии с (7) максимальное требуемое отношение сигнал/импульсная помеха, обеспечивающее заданную вероятность ошибки,

При действии двух видов помех их общая спектральная плотность определяется выражением [Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи: базовые методы и характеристики: учеб. пособие. - М.: Эко-Трендз, 2005. С. 229, формула (7.25)]

где - спектральная плотность преднамеренной помехи.

В соответствии с (14) среднее значение спектральной плотности равно .

Тогда отношение сигнал/суммарная помеха должно рассчитываться по формуле

то есть при энергетическом подходе, когда , отношение сигнал/ суммарная помеха принимает вид

В реализуемом прототипом случае, когда действие непрерывной помехи не учитывается (α₀=∞) и наихудшей импульсной помехой признается та, которая максимизирует вероятность ошибки Р_{ош б}, соответствующие параметры системы принимают значения (см. (1), (2) с учетом (4) и (15))

Попытаемся применить к (17) - (19) энергетический подход к оценке помехоустойчивости системы, полагая ; .

Тогда из (18) получим

а из (17), (19) требуемые для обеспечения заданной вероятности ошибки отношения сигнал/импульсная помеха и сигнал/суммарная помеха

Сравнивая (12) и (20), видим, что

где

Аналогично, сравнив (13) и (21), с учетом (23) получим

где

Наконец, в результате сравнения (16) и (22) с учетом (25) имеем

где

Следовательно, новым по сравнению с прототипом признаком является введение поправочных коэффициентов k₁(α₀), k₂(α₀), k₃(α₀), позволяющих учесть влияние непрерывной помехи (шума приемника) на соответствующие показатели помехоустойчивости СРС, а также применить в этих условиях энергетический подход к оценке помехоустойчивости системы.

Данный признак обладает существенными отличиями, т.к. в известных способах не обнаружен.

Покажем на конкретном примере, что применение предлагаемого способа позволяет уточнить значения указанных выше показателей помехоустойчивости СРС за счет учета влияния непрерывной помехи (шума приемника).

Для заданных выше исходных данных α₀=10 и Р_{ош зад}=10^-2 получим:

а) при предлагаемом способе в соответствии с (12), (13), (16)

б) при способе-прототипе в соответствии с (20), (21), (22)

Таким образом, учет того, что в действующей на входе приемника смеси двух помех есть не только наихудшая (оптимальная) импульсная помеха, но и слабая непрерывная, позволяет уточнить оптимальные значения требуемых для достижения заданной вероятности ошибки Р_{ош зад}=10^-2 показателей помехоустойчивости СРС:

а) доля поражаемой импульсной помехой полосы частот увеличивается

в ;

б) отношение сигнал/импульсная помеха увеличивается

в ;

в) отношение сигнал/суммарная помеха уменьшается

в .

Реализация предлагаемого способа возможна как с помощью средств вычислительной техники, так и с помощью устройства, структурная схема которого приведена на фиг. В состав устройства входят такие элементы, как четыре делителя 2, шесть умножителей 3, три вычитателя 4, два сумматора 5, вычислитель квадратного корня 6, функциональный преобразователь 7. Указанные элементы (блоки) известны и приводятся в соответствующей литературе [Горошков Б.И. Элементы радиоэлектронных устройств: Справочник. - М.: Радио и связь, 1988; Угрюмов Е.П. Цифровая схемотехника. – СПб.: БХВ-Петербург, 2005; Цифровые устройства на интегральных микросхемах. - 3-е изд. перераб. и доп. - М.: Радио и связь, 1991 - (Массовая радиобиблиотека. Вып. 1159); Цифровые и аналоговые интегральные микросхемы. Справочник/под. ред. С.В. Якубовского. М.: Радио и связь, 1989].

Устройство реализует соотношения (12), (13), (16) и работает следующим образом.

Информация об энергии принимаемого сигнала Е_б с первого выхода блока задания исходных данных 1 поступает на вход делимого первого делителя 2, на вход делителя которого со второго выхода блока задания исходных данных 1 поступает информация о спектральной плотности шума N₀. Результат деления с выхода первого делителя 2 поступает на вход делимого второго делителя 2, вход вычитаемого первого вычитателя 4, вход уменьшаемого третьего вычитателя 4, а также на первые входы второго сумматора 5, четвертого и шестого умножителей 3. Константа, равная 1, с третьего выхода блока задания исходных данных 1 поступает на оба входа первого сумматора 5, с выхода которого константа 2 подается на первый вход второго умножителя 3 и вход делителя второго делителя 2, с выхода которого результат деления поступает на вход уменьшаемого второго вычитателя 4, а также на оба входа первого умножителя 3, с выхода которого результат умножения поступает на вход уменьшаемого первого вычитателя 4, с выхода которого результат вычитания поступает на вход вычислителя квадратного корня 6, с выхода которого значение поступает на вход вычитаемого второго вычитателя 4, с выхода которого результат вычитания - поступает на вход вычитаемого третьего вычитателя 4 и второй вход четвертого умножителя 3, а также на вход показателя степени функционального преобразователя 7. Информация о заданной вероятности ошибки на бит Р_{ош зад} с четвертого выхода блока задания исходных данных 1 подается на второй вход второго умножителя 3, с выхода которого результат умножения 2Р_{ош зад} поступает на первый вход третьего умножителя 3. С пятого выхода блока задания исходных данных 1 значение числа е подается на вход основания степени функционального преобразователя 7, с выхода которого результат преобразования поступает на второй вход третьего умножителя 3, с выхода которого и выдается оптимальное значение первого искомого показателя - части полосы частот, поражаемой импульсной помехой . Это значение поступает на первый вход пятого умножителя 3, на второй вход которого подается результат вычитания х₁+α₀ с выхода третьего вычитателя 4. Результат перемножения с выхода пятого умножителя 3 подается на вход делителя третьего делителя 2, на вход делимого которого поступает результат перемножения -α₀х₁ с выхода четвертого умножителя 3. Полученное на выходе третьего делителя 2 значение является вторым искомым показателем - отношением сигнал/импульсная помеха, которое поступает на вторые входы второго сумматора 5 и шестого умножителя 3. На вход делимого четвертого делителя 2 подается результат перемножения с выхода шестого умножителя 3, а на вход делителя - результат сложения с выхода второго сумматора 5. Полученное на выходе четвертого делителя 2 значение - является третьим искомым показателем - отношением сигнал/суммарная помеха.

Для наглядности и с целью упрощения описания формулы изобретения сведем аналитические выражения для искомых показателей в таблицу 1.

Способ определения оптимальных значений показателей устойчивости системы связи с широкополосными сигналами к одновременному воздействию непрерывной и импульсной помех, заключающийся в том, что в качестве первого показателя принимают поражаемую импульсной помехой часть полосы частот , рассчитываемую как произведение удвоенного заданного значения вероятности ошибки P_{ош зад} на число , представляющее собой основание натурального логарифма, в качестве второго показателя - максимальное отношение сигнал/импульсная помеха , требуемое для обеспечения приема информации с вероятностью ошибки не более заданной и рассчитываемое по формуле , а в качестве третьего показателя – отношение энергии сигнал/суммарная помеха , совпадающее с предыдущим показателем, отличающийся тем, что для получения оптимальных значений этих показателей с учетом непрерывной помехи (шума приемника) значение умножают на коэффициент k₁(α₀), который рассчитывают по формуле , где x₁ рассчитывают по формуле , а значение α₀ вычисляют как отношение энергии сигнала Е_б к спектральной плотности шума N₀; значение умножают на коэффициент k₂(α₀), рассчитываемый по формуле , а значение умножают на коэффициент k₃(α₀), рассчитываемый по формуле .