Способ адаптивного выбора оптимального параметра алгоритма коррекции сигналов

Способ адаптивного выбора оптимального параметра алгоритма коррекции сигналов

Иллюстрации

Показать все

Реферат

Изобретение относится к технике связи и может быть использовано в системах передачи данных с адаптивной коррекцией сигналов для выбора параметра алгоритма коррекции.

Во многих системах передачи данных для компенсации искажений, внесенных каналом связи, применяют алгоритмы адаптивной коррекции сигналов. Для этого в передаваемый сигнал осуществляют периодические вставки известного на приемной стороне тестового сигнала. Такой подход используется, например, в стандарте авиационной передачи данных ARINC-635 [1].

Известно большое количество различных методов, алгоритмов и их модификаций, используемых для коррекции сигналов, например метод наименьших квадратов или алгоритм LMS [2], алгоритм RLS [3], метод регуляризации Тихонова [4]. Во всех этих и многих других алгоритмах для обеспечения устойчивости и сходимости вводят некоторый параметр, в частности параметр регуляризации (алгоритм RLS, метод регуляризации Тихонова), размер шага сходимости (алгоритм LMS). Выбор того или иного параметра оказывает существенное влияние не только на устойчивость решения, но и на вероятность ошибки на бит после демодуляции откорректированного сигнала, т.е. на помехоустойчивость.

Как известно, задача адаптивной коррекции сводится к решению двух уравнений, которые можно записать в следующей форме:

где K(t) - передаваемый тестовый сигнал, u(t) - принимаемый тестовый сигнал, K_m(t) - передаваемый информационный сигнал, u_m(t) - принимаемый информационный сигнал, h(t) - импульсная характеристика канала, * - оператор свертки.

Из уравнения (1) получают приближенную импульсную характеристику канала в общем случае в виде:

а результат коррекции в этом случае можно записать в виде:

где R{} - некоторый алгоритм расчета, α₁, α₂ - параметры, используемые для устойчивости алгоритма. Отметим, что в большинстве практических случаев допустимо принять:

тогда вместо (5) запишем:

Известны различные способы выбора оптимального значения этого параметра.

Наиболее близким к заявленному техническому решению является способ невязки, описанный в [5]. Этот способ часто применяют для выбора параметра регуляризации в методе регуляризации Тихонова. В условиях (3) (6) способ невязки заключается в том, что, используя алгоритм R{} на основе поступившего тестового сигнала u₀(t), рассчитывают импульсную характеристику канала h(t,α) и корректирующего фильтра h_коp(t,α), с помощью которой, используя некоторый алгоритм R{}, корректируют поступивший информационный сигнал u_m(t), в результате чего получают откорректированный информационный сигнал K_m(t,α), после чего определяют значение ошибки е, в качестве которой служит разница среднеквадратичного уклонения откорректированного информационного сигнала K_m(t,α), свернутого с рассчитанной импульсной характеристикой канала h(t,α), от принятого информационного сигнала u_m(t) и дисперсии шумовой составляющей Δu, т.е. , после чего определяют зависимость значения ошибки е от параметра α путем изменения значения этого параметра, в результате чего получают оптимальное значение параметра α_opt, обеспечивающего минимальное значение ошибки е.

Недостатком прототипа является необходимость знания определенной априорной информации, а именно дисперсии шумовой составляющей, оценка которой является отдельной достаточно сложной задачей и имеет определенную погрешность. Кроме того, при вычислении значения ошибки е вносится дополнительная погрешность при свертке приближенных (рассчитанных) значений K_m(t,α) и h(t,α).

Целью изобретения является выбор оптимального параметра алгоритма коррекции сигналов без знания априорной информации и без внесения дополнительной погрешности, т.е. увеличение точности оценки α_opt.

Поставленная цель достигается тем, что способ адаптивного выбора оптимального параметра алгоритма коррекции сигналов, заключающийся в том, что, используя алгоритм R{} на основе поступившего тестового сигнала u₀(t), рассчитывают импульсную характеристику корректирующего фильтра h_кор(t,α), отличающийся тем, что с помощью импульсной характеристики корректирующего фильтра h_кop(t,α), используя алгоритм R{}, корректируют поступившие тестовые сигналы u₁(t)…u_n(t), задержанные на интервал, равный длине информационного сигнала L_И, в результате чего получают откорректированные тестовые сигналы K₁(t,α)…K_n(t,α), определяют значения ошибки е₁…е_n, в качестве которой служит среднеквадратичное уклонение откорректированного тестового сигнала K₁(t,α)…K_n(t,α) от образцового тестового сигнала K(t), т.е. , j=1…n, после чего определяют зависимость значения ошибки е₁…е_n от параметра α путем изменения значения этого параметра, в результате чего получают массив значений параметров α₁…α_n, обеспечивающих соответствующее минимальное значение ошибки е₁…е_n для каждого откорректированного тестового сигнала K₁(t,α)…K_n(t,α), после чего из массива α₁…α_n осуществляют окончательный выбор оптимального значения параметра α_opt, в качестве которого, в зависимости от конкретного алгоритма R{} и диапазона значений параметров α₁…α_n, берут среднее арифметическое значение или медианное значение из массива α₁…α_n.

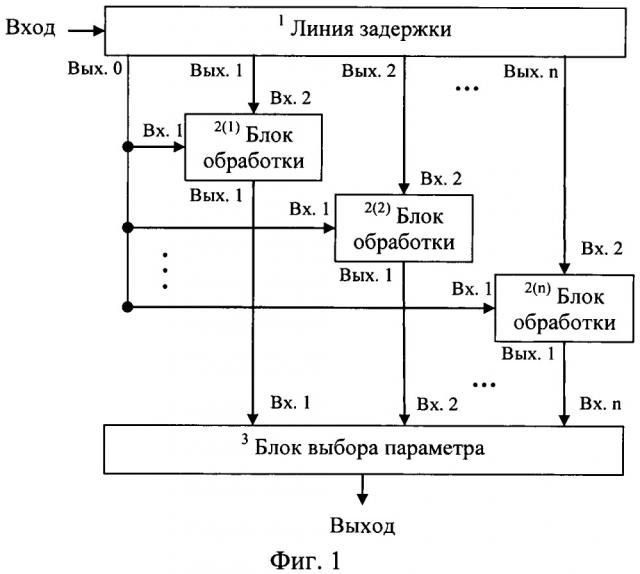
На фиг. 1, 2 представлена структурная схема способа адаптивного выбора оптимального параметра алгоритма коррекции сигналов.

Она содержит:

1 - линию задержки;

2(1)-2(n) - блок обработки;

3 - блок выбора параметра.

В свою очередь каждый блок обработки 2(1)-2(n) содержит:

2.1 - блок расчета импульсной характеристики;

2.2 - корректирующий фильтр;

2.3 - блок оценки ошибки;

2.4 - решающее устройство.

Работа способа осуществляется следующим образом. На вход линии задержки 1 поступает сигнал, содержащий периодически повторяющиеся тестовые и информационные сигналы. Структура такого сигнала представлена на фиг. 3. При этом длина каждого тестового сигнала составляет L_T, длина каждого информационного сигнала L_И. Количество отводов (выходов) линии задержки 1, равное n+1, может быть различным и выбирается исходя из конкретного применения. С каждого из n+1 выходов линии задержки 1 поступают тестовые сигналы u₀(t)…u_n(t) длиной L_T, задержанные на интервал, равный длине информационного сигнала L_И. При этом с 0-го выхода линии задержки 1 тестовый сигнал подают на первый вход каждого блока обработки 2(1)-2(n), на второй вход которых поступают тестовые с выходов 1…n линии задержки 1, а именно с 1-го выхода линии задержки 1 на второй вход блока обработки 2(1), со 2-го выхода линии задержки 1 на второй вход блока обработки 2(2) и т.д.

В каждом блоке обработки 2(1)-2(n) осуществляют следующее.

Поступивший с первого входа блока обработки 2(1)-2(n) тестовый сигнал u₀ подают на вход блока расчета импульсной характеристики 2.1, с выхода которого импульсную характеристику корректирующего фильтра h_кop(t,α) подают на первый вход корректирующего фильтра 2.2. При этом на второй вход корректирующего фильтра 2.2 подают соответствующий тестовый сигнал u₁(t)…u_n(t), поступивший со второго входа блока обработки 2(1)-2(т). На выходе корректирующего фильтра 2.1 получают соответствующий откорректированный тестовый сигнал K₁(t,α)…K_n(t,α), который подают на вход блока оценки ошибки 2.3. При этом в блоке расчета импульсной характеристики 2.1 и корректирующем фильтре 2.2 используют один и тот же алгоритм, обозначенный ранее как R{}. В блоке оценки ошибки 2.3 получают значение ошибки, в качестве которой служит среднеквадратичное уклонение откорректированного тестового сигнала K₁(t,α)…K_n(t,α) от образцового тестового сигнала K(t), т.е., j=1…n. Полученное на выходе блока оценки ошибки 2.3 значение ошибки е₁…е_n подают на вход решающего устройства 2.4, в котором определяют зависимость значения ошибки е₁…е_n от параметра α путем изменения значения этого параметра на первом выходе решающего устройства 2.4 и передаче его на управляющие входы блока расчета импульсной характеристики 2.1 и корректирующего фильтра 2.2. В результате на втором выходе решающего устройства 2.4, являющегося выходом блока обработки 2(1)-2(n), получают значение параметра α₁…α_n, обеспечивающего минимальное значение ошибки е₁…е_n.

Полученные на выходе блоков обработки 2(1)-2(n) значения параметра, представляющие собой массив α₁…α_n, подают на соответствующие входы блока выбора параметра 3. В блоке выбора параметра 3 осуществляют окончательный выбор параметра α, получая на выходе оптимальное значение параметра α_opt. В зависимости от конкретного алгоритма R{} и возможного диапазона значений параметров α₁…α_n, поступивших на входы блока выбора параметра 3, в качестве оптимального значения параметра α_орt берут среднее арифметическое значение:

или медианное значение, соответствующее:

где массив α₁'…α_n’ соответствует отсортированным по возрастанию значениям α₁…α_n.

Техническим результатом является выбор оптимального параметра алгоритма коррекции сигналов с увеличенной точностью оценки α_opt.

Список источников

1. ARINC Characteristic 635-4. HF Data Link Protocol. - Dec., 2003.

2. Джиган В.И. Адаптивная фильтрация сигналов: теория и алгоритмы. - М.: Техносфера, 2013. - 528 с.

3. Sayed А.Н. Adaptive filters. - New Jersey: Hoboken: John Wiley & Sons, Inc., 2008. - 786 c.

4. Тихонов A.H., Арсенин В.Я. Методы решения некорректных задач / Учебное пособие для вузов. - Изд. 3-е испр. - М.: Наука, 1986. - 288 с.

5. Верлань А.Ф., Сизиков B.C. Методы решеня интегральных уравнений с программами для ЭВМ. Справочное пособие. - Киев: Наукова думка, 1978. - 292 с.

Способ адаптивного выбора оптимального параметра алгоритма коррекции сигналов заключается в том, что используя алгоритм R{} на основе поступившего тестового сигнала u₀(t) рассчитывают импульсную характеристику корректирующего фильтра h_коp(t,α), отличающийся тем, что с помощью импульсной характеристики корректирующего фильтра h_коp(t,α), используя алгоритм R{}, корректируют поступившие тестовые сигналы u₁(t)…u_n(t), задержанные на интервал, равный длине информационного сигнала L_И, в результате чего получают откорректированные тестовые сигналы K₁(t,α)…K_n(t,α), определяют значения ошибки е₁…e_n, в качестве которой служит среднеквадратичное уклонение откорректированного тестового сигнала K₁(t,α)…K_n(t,α) от образцового тестового сигнала K(t), т.е. , j=1…n, после чего определяют зависимость значения ошибки е₁…e_n от параметра α путем изменения значения этого параметра, в результате чего получают массив значений параметров α₁…α_n, обеспечивающий соответствующее минимальное значение ошибки е₁…e_n для каждого откорректированного тестового сигнала K₁(t,α)…K_n(t,α), после чего из массива α₁…α_n осуществляют окончательный выбор оптимального значения параметра α_opt, в качестве которого, в зависимости от конкретного алгоритма R{} и диапазона значений параметров α₁…α_n, берут среднее арифметическое значение или медианное значение из массива α₁…α_n.