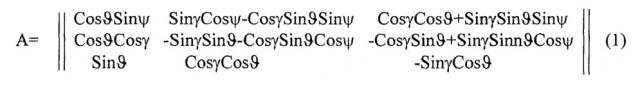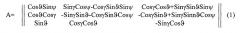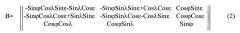Комбинированная бесплатформенная астроинерциальная навигационная система

Комбинированная бесплатформенная астроинерциальная навигационная система

Иллюстрации

Показать все

Реферат

Изобретение относится к области корректируемых инерциальных навигационных систем и может быть использовано при разработке комплексированных навигационных систем, в которых основная навигационная информация, поставляемая бесплатформенными инерциальными навигационными системами (БИНС), корректируется по позиционной и скоростной информации, поставляемой спутниковой навигационной системой (СНС), и угловой информацией, поставляемой астросистемой.

Далее при описании предлагаемой системы в тексте используются следующие обозначения:

- векторы и матрицы обозначаются жирным шрифтом;

- надстрочный индекс " ' " обозначает операцию дифференцирования;

- надстрочный индекс "" обозначает операцию транспонирования;

- надстрочный индекс обозначает операцию обращения матрицы;

- надстрочный индекс "", стоящий после матрицы, обозначает кососимметрическую матрицу.

При описании системы используются следующие ортогональные системы координат (трехгранники):

- трехгранник Oh₁h₂h₃, лежащий в плоскости Гринвичского меридиана, ось Oh₃ направлена на северный полюс;

- идеальный (сопровождающий) трехгранник Mx₁x₂x₃ с началом в точке М, связанной с объектом, ось x₃ совпадает с местной вертикалью;

- модельный трехгранник My₁y₂y₃, реализуемый бортовой ЦВМ;

- приборный трехгранник Mz₁z₂z₃, связанный со строительными осями системы (блока чувствительных элементов).

Взаимная ориентация трехгранников Mx₁x₂x₃ и My₁y₂y₃ определяется вектором α малых углов поворота.

Взаимная ориентация трехгранников Mz₁z₂z₃ и My₁y₂y₃ задается матрицей ориентации А.

где: ϑ, γ, Ψ - углы крена, тангажа и гироскопического курса соответственно.

Ориентация трехгранника My₁y₂y₃ относительно трехгранника Oh₁h₂h₃ задается матрицей направляющих косинусов В:

где: ϕ, λ, ε - географические координаты и курсовой угол.

Стандартная блок-схема, по которой строится коррекция навигационной системы по внешней информации, представлена на Фиг. 1, где:

G - импульсная переходная функция объекта регулирования;

Н - матрица связи вектора корректируемых параметров системы x и вектора измерения z;

K - коэффициент усиления сигнала.

На один вход разностной блок-схемы подается сигнал Hx, а на другой - измерение z. Полученная разность (невязка) z-Hx подается на вход блока обратной связи с коэффициентом усиления К, выход которого подключен к входу блока G. Математическая запись системы, представленной на Фиг. 1, имеет вид:

Примером системы, использующей такую схему коррекции инерциальной системы по внешней скоростной информации, поставляемой доплеровским измерителем скорости и угла сноса (ДИСС), является известная астроинерциальная навигационная система, реализованная в серийных астроинерциальных системах Л-14МА [1] и Л41 [2], входящих в состав навигационных комплексов ВП-021 и Н-202.

Известная астроинерциальная навигационная система состоит из телеблока, установленного в рамках двухосного карданова подвеса, обеспечивающего выставку телеблока на заданные углы А (азимут) и В (высота), снабженного датчиками его углов, двигателями отработки углов его выставки, и установленного либо на гироплатформе, либо в рамках внешнего карданова подвеса - повторителя горизонта (в зависимости от конструкции системы), бортовой ЦВМ, блока следящих систем отработки углов наведения визирной оси телеблока по целеуказаниям бортовой ЦВМ, содержащего первую и вторую разностные схемы, блоков коррекции, блока определения разностей ΔА, ΔВ между расчетными и фактическими значениями этих углов, блока пересчета разностей ΔА, ΔВ в вектор β кинематических ошибок системы, источника внешней скоростной информации в виде ДИСС, блока вычисления ошибок определения угловой скорости Δω и ошибок построения вертикали α, а также третьей разностной схемы, в которой вычисляется вектор γ позиционной ошибки системы.

Известная система работает следующим образом.

В бортовой ЦВМ из записанного каталога звезд выбирается пара звезд, доступных визированию в заданный момент времени для заданной точки местоположения объекта, и последовательно проводится их визирование с определением разностей между расчетными и фактическими значениями углов их визирования, которые затем пересчитываются в вектор β кинематических ошибок системы. Поскольку вектор β представляет алгебраическую сумму вектора α ошибок построения вертикали и вектора γ позиционной ошибки, то в существующей системе для более точного определения вектора γ привлекается дополнительная скоростная информация от ДИСС, по которой определяется вектор α ошибок построения вертикали, а также искомый вектор γ позиционной ошибки системы.

Связь между угловыми поправками, получаемыми при визировании звезд, и кинематическими ошибками инерциальной навигационной системы определяется линейным соотношением:

или в скалярной форме:

где:

z - вектор угловых поправок (вектор измерения);

- вектор кинематических ошибок системы;

Н - матрица связи, структура которой определяется схемой подвеса телеблока и кинематикой отработки его углов наведения; h₁, h₂, h₃ - элементы матрицы Н.

Для однозначного определения трех компонент вектора β требуется как минимум три невырожденных уравнения (4). Поскольку при визировании одной звезды получаем два измерения (две угловые поправки), для решения уравнения (4)требуется проведение измерений как минимум двух звезд.

В обеих системах при построении фильтра ставилась задача оценки ошибок построения вертикали, скоростных ошибок и линейной комбинации кинематических ошибок системы, инструментальных ошибок (некомпенсированные дрейфы и ошибки акселерометров), и ошибок измерения, вызванных ошибками взаимной привязки осей корректируемой системы и антенн ДИСС. Базовой при построении фильтра скоростной коррекции (импульсная переходная функция G) была принята динамическая группа уравнений ошибок системы (6)-(11), приведенная ниже.

Асимптотически устойчивый фильтр шестого порядка, реализованный в системе Л-14МА, обеспечивал готовность оценок ошибок построения вертикали и скоростной ошибки за время, превосходящее 30 минут, а фильтр того же порядка, реализованный в системе Л41 с использованием метода калмановской фильтрации (метод корня), обеспечивал готовность оценок ошибок построения вертикали и скоростной ошибки за 12 минут времени. Однако, ошибки внешней скоростной информации, вызванные ошибками взаимной привязки осей корректируемой системы и антенн ДИСС, приводят к дополнительным ошибкам корректируемых параметров инерциальной системы.

Задачей предлагаемого изобретения является разработка комлексированной астроинерциальной навигационной системы, в которой повышается точность определения ошибок БИНС, а также надежность ее работы.

Поставленная задача решается астроинерциальной навигационной системой, содержащей систему определения корректирующих поправок бесплатформенной инерциальной навигационной системы и источники внешней информации, сигналы с которых используются в качестве входной информации для определения корректирующих поправок, причем, в качестве первого источника внешней информации применен источник астроинформации, включающий телеблок, установленный в рамках карданова подвеса, обеспечивающего выставку телеблока на заданные углы по азимуту и высоте, блок следящих систем отработки углов наведения визирной оси телеблока, бортовую ЦВМ, по целеуказаниям которой следящие системы отрабатывают эти углы, а также блок вычисления угловых поправок, причем, в качестве второго источника внешней информации применен источник скоростной и позиционной информации, а система определения корректирующих поправок бесплатформенной инерциальной навигационной системы выполнена трехступенчатой и включает последовательно подключенные блок определения позиционной ошибки, скоростной ошибки и ошибки построения вертикали, обеспечивающий на выходе первой ступени формирование горизонтальных проекций вектора кинематических ошибок системы, как результат визирования гипотетической звезды, находящейся в зените, входами связанный с бортовой ЦВМ и источником скоростной и позиционной информации, блок определения вертикальной проекции вектора кинематических ошибок системы, обеспечивающий на выходе второй ступени формирование вектора кинематических ошибок системы, и подключенный вторым входом к блоку вычисления угловых поправок, а также блок определения инструментальных ошибок системы, обеспечивающий на выходе третьей ступени формирование вектора нескомпенсированных дрейфов системы на оси приборного трехгранника.

Таким образом, предложенная система отличается от известной тем, что источник внешней скоростной информации (ДИСС) заменен на источник скоростной и позиционной информации (спутниковая система навигации - СНС), и соответственно, блок определения скоростной ошибки и ошибки построения вертикали инерциальной системы заменен на блок определения позиционной и скоростной ошибок и ошибки построения вертикали. Эти два блока составляют первую ступень, выходом которой являются оценки β₁, β₂ вектора β кинематических ошибок системы. Блок определения вектора β кинематических ошибок системы заменен на блок определения вертикальной проекции (компоненты β₃) вектора β кинематических ошибок системы, который составляет вторую ступень, и введен блок определения инструментальных ошибок системы (вектора v нескомпенсированных дрейфов системы в проекциях на оси приборного трехгранника) - третья ступень.

При создании системы учитывается то обстоятельство, что в совокупности определяемых ошибок системы такие ошибки как ошибка α построения вертикали и ошибки γ определения местоположения являются двухкомпонентными векторами, определяемыми в проекциях на оси сопровождающего трехгранника (местного горизонта), а кинематические ошибки β и инструментальные ошибки системы ν, ε (некомпенсированные дрейфы и ошибки акселерометров) являются трехкомпонентными векторами, при этом инструментальные ошибки ν, ε, которые рассматриваются как систематические ошибки, определены в проекциях на оси приборного трехгранника, ориентированного в БИНС относительно сопровождающего трехгранника, как было сказано выше, произвольным образом. Взаимная ориентация этих трехгранников определяется матрицей ориентации (1).

Учет этих особенностей позволил создать трехступенчатую систему, на первой ступени которой, представляющей двухканальную систему, определяются такие ошибки системы, как ошибка определения координат γ, скоростная ошибка Δω, ошибка построения вертикали α. Полученные оценки ошибок БИНС используются как новый вектор измерения, поступающий на вход алгоритма второй ступени, решающей задачу определения вектора β кинематических ошибок, на третьей ступени, представляющей собой трехканальную систему, определяются такие инструментальные ошибки как нескомпенсированные дрейфы системы ν.

Предложенная астроинерциальная навигационная система, представлена на Фиг. 2 в виде структурной блок-схемы, и состоит из телеблока 1, установленного в рамках карданова подвеса, снабженного датчиками его углов по азимуту 2 и высоте 3, двигателями отработки углов его выставки по азимуту 4 и высоте 5, бортовой ЦВМ 6, блока 7 следящих систем отработки углов наведения визирной оси телеблока, содержащего первую 8 и вторую 9 разностные схемы, первого 10 и второго 11 блоков коррекции, а также блока 12 вычисления угловых поправок. Бортовая ЦВМ 6 выходами подключена к блоку 7, второй вход первой разностной схемы 8 подключен к выходу датчика 3, второй вход второй разностной схемы 9 подключен к выходу датчика 2, а выходы подключены к входам первого 10 и второго 11 блоков коррекции. Выход первого блока коррекции 10 подключен к входу двигателя 4, выход второго блока коррекции 11 подключен к входу двигателя 5, а блок 12 первым входом подключен к выходу двигателя 4, вторым входом подключен к выходу двигателя 5, а третьим входом - к третьему выходу бортовой ЦВМ 6. Блок 12 выходом подключен к входу блока 13 определения вертикальной проекции вектора кинематических ошибок системы, выход которого подключен к входу блока 14 определения инструментальных ошибок системы, а вход подключен к входу блока 15 определения позиционной ошибки, скоростной ошибки и ошибки построения вертикали, подключенного первым входом к источнику скоростной и позиционной информации 16 (СНС), а вторым входом - к четвертому выходу бортовой ЦВМ 6.

Предложенная система работает следующим образом.

В качестве базовых при построении алгоритма оценки ошибок БИНС используются уравнения, описывающие поведение динамических и кинематических ошибок в проекциях на оси сопровождающего трехгранника классической платформенной системы [1], [2], в которых учтены особенности построения БИНС.

где:

Δω₁, Δω₂ - скоростные ошибки системы;

α₁, α₂ - ошибки построения вертикали;

β - вектор кинематических ошибок системы;

δε₁, δε₂, δω - проекции векторов инструментальных ошибок ε, ν (ошибок акселерометров, некомпенсированных дрейфов системы соответственно) на оси сопровождающего трехгранника, определяемые как:

где:

ε, ν - систематические составляющие векторов инструментальных ошибок системы (ошибок акселерометров, некомпенсированных дрейфов системы соответственно), определенные в проекциях на оси приборного трехгранника, как:

А - матрица ориентации, определяемая по (1);

ω - кососимметрическая матрица, соответствующая вектору абсолютных угловых скоростей вращения сопровождающего трехгранника:

где:

b₁₃, b₂₃ - элементы матрицы направляющих косинусов В, определяемые по (2);

V₁, V₂ - линейные скорости движения объекта;

R - радиус Земли;

u = 15 град/час - скорость вращения Земли.

Прежде чем приступать к описанию работы системы определения ошибок корректируемой инерциальной системы по внешней позиционной и скоростной информации (первая ступень), проведем стандартную процедуру выделения наблюдаемого подпространства.

Задача построения наблюдаемого подпространства и определения меры наблюдаемости достаточно подробно и исчерпывающе изложена в [5].

Необходимым и достаточным условием наблюдаемости линейной динамической системы (6)-(9) является максимальный ранг матрицы наблюдаемости, равный размерности системы:

где:

A=E+Gdt;

Е - единичная матрица;

dt - шаг интегрирования.

В основе процедуры построения наблюдаемого подпространства лежит преобразование:

где:

Т - невырожденная матрица, структура которой может быть представлена в виде:

приводящее систему к каноническому виду, в котором импульсная переходная функция будет иметь вид:

с матрицей связи вектора измерения z с вектором x оцениваемых параметров системы:

или блочный вид:

где:

& - элементы матрицы, отличные от нуля;

* - элементы матрицы, которые могут отличаться от нуля.

Процедура заключается в определении элементов x_i вектора x наблюдаемых параметров. Обозначим:

где Δω₁, Δω₂, γ₁, γ₂ определяются как:

ϕ_снс, λ_снс - географические широта и долгота, поставляемые СНС;

ϕ, λ - географические широта и долгота, поставляемые инерциальной системой;

γ₁, γ₂, Δϕ, Δλ - элементы вектора измерения z, формируемого по внешней позиционной и скоростной информации, т.е. наблюдаемыми величинами.

Подставляя х₁, х₂, х₅, х₆ в (6)-(8) получаем:

где:

Здесь при дифференцировании х₂, х₃, x₆, х₇ сделаны допущения о равенстве нулю производных членов поскольку эти производные представляют величины второго порядка малости.

В результате проделанных преобразований получили автономную систему, в новых переменных x_i,i = 1,2,…,8

переходная матрица которой имеет форму жордановой матрицы:

вида (19) с матрицей связи:

т.е. наблюдаемую систему.

Сделанные выше допущения о малости переменных позволили построить относительно простую наблюдаемую систему четвертого порядка по каждому каналу.

Построенная система в новых (наблюдаемых) переменных x_i представляет первую (двухканальную) ступень системы определения корректирующих поправок.

Структурно блок-схема первой ступени, относящейся к блоку 15 (Фиг. 2), и входящей в состав представленной на Фиг. 3 трехступенчатой системы определения корректирующих поправок, состоит из третьей 44, четвертой 45, пятой 46 и шестой 47 разностных схем, первыми входами подключенных к выходу СНС 16 и вторыми к выходу бортовой ЦВМ 6, и восьми цепей (по четыре в каждом канале). Третья 44 и пятая 46 разностные схемы связаны своими выходами с первой цепью из последовательно соединенных первого усилителя 36, первого сумматора 17, первого интегратора 23 и седьмой разностной схемы 48, со второй цепью из последовательно соединенных второго усилителя 37, второго сумматора 18 и второго интегратора 24, с третьей цепью из последовательно соединенных третьего усилителя 38, третьего сумматора 19 и третьего интегратора 25, а также с четвертой цепью из последовательно соединенных четвертого усилителя 39 и четвертого интегратора 26. Четвертая 45 и шестая 47 разностные схемы связаны своими выходами с пятой цепью из последовательно соединенных пятого усилителя 40, четвертого сумматора 20 и пятого интегратора 27, с шестой цепью из последовательно соединенных шестого усилителя 41, пятого сумматора 21 и шестого интегратора 28, с седьмой цепью из последовательно соединенных седьмого усилителя 42, шестого сумматора 22 и седьмого интегратора 29, а также с восьмой цепью из последовательно соединенных восьмого усилителя 43 и восьмого интегратора 30. Первый сумматор 17 вторым входом подключен к выходу второго интегратора 24, а третьим входом через одиннадцатый усилитель 33 с коэффициентом усиления ω₃ к выходу пятого интегратора 27. Второй сумматор 18 вторым входом подключен через десятый усилитель 32 к одному из выходов третьего интегратора 25, а третьим входом через двенадцатый усилитель 34 к выходу шестого интегратора 28. Третий сумматор 19 вторым входом подключен к выходу четвертого интегратора 26, а третьим входом к выходу второго интегратора 24. Четвертый сумматор 20 вторым входом подключен к одному из выходов шестого интегратора 28, а третьим входом через девятый усилитель 31 с коэффициентом усиления -ω₃ к выходу первого интегратора 23. Пятый сумматор 21 вторым входом подключен через четырнадцатый усилитель 50 с коэффициентом усиления -2u к выходу второго интегратора 24, а третьим входом через тринадцатый усилитель 35 к выходу седьмого интегратора 29. Шестой сумматор 22 вторым входом подключен к выходу восьмого интегратора 30, а третьим входом к одному из выходов шестого интегратора 28, оставшийся выход которого подключен к третьему входу четвертой разностной схемы 47. Первый интегратор 23 подключен своими выходами к третьему входу третьей разностной схемы 44 и первому входу седьмой разностной схемы 48, подключенной вторым входом к одному из выходов второго интегратора 24, который оставшимися выходами подключен к третьему входу пятой разностной схемы 46 и второму входу девятого усилителя 31, к третьему входу которого подключен одним из выходов четвертый интегратор 26, а третьим входом подключенной к одному из выходов третьего интегратора 25. Пятый интегратор 27 одним из выходов подключен к третьему входу четвертой разностной схемы 45, к четвертому входу которой подключен один из выходов восьмого интегратора 30, а последним выходом к первому входу восьмой разностной схемы 49, подключенной вторым входом к одному из выходов седьмого интегратора 29.

Первая ступень работает следующим образом.

На входы третьей и четвертой разностных схем 44 и 45 из СНС 16 и бортовой ЦВМ 6 выдается информация о местоположении объекта, в результате чего формируются разности γ₁, γ₂, являющиеся измерениями первого и второго каналов. Одновременно, на входы этих разностных схем выдаются выходные сигналы первого 23 и пятого 27 интеграторов, в результате чего на их выходах формируются невязки, которые выдаются с выхода третьей разностной схемы 44 на входы усилителей 36, 37, 38, 39 первого канала и с выхода четвертой разностной схемы 45 на входы усилителей 40, 41, 42, 43 второго канала, в результате чего на выходе этих усилителей формируется сигнал обратной связи K(z-Hx). Выбор коэффициентов усиления в цепи обратной связи может производиться любым из известных способов, и не входит в рассмотрение данной заявки. В частности, для определения коэффициентов усиления может применяться асимптотически-устойчивый способ, по которому выбранные коэффициенты усиления обеспечивают равные корни рассматриваемой системы, обеспечивающие ее сходимость с заданным коэффициентом затухания 0<λ<1; при определении коэффициентов усиления может быть использован критерий Гаусса:

где:

Z - вектор измерений;

Н - матрица связи вектора измерений с вектором % оцениваемых параметров;

D - матрица весовых коэффициентов;

т - операция транспонирования,

и построенный на базе этого критерия Гаусса фильтр Калмана; определенную привлекательность представляет критерий оптимальности, предложенный в свое время Чебышевым, минимизирующий кусочно-линейную форму:

где: m - число измерений.

Привлекательность использования критерия (46) заключается в том, что в отличии от критерия (45) определяется не доверительный, а гарантированный интервал за рамки которого не выходит ошибка оценки, полученной в данной конкретной реализации - метод, получивший название метода гарантированной оценки.

Слагаемые, поступающие на входы сумматоров 17, 18, 19 и 20, 21, 22 представляют суммы правых частей уравнений (30)-(38), интегрируя которые интеграторами 23-26 для перового канала и интеграторами 27-30 для второго канала, получаем оценки x_i,i = 1-8 ошибок системы в соответствии с (30)-(37).

Выходом этой ступени являются оценки β₁, β₂ горизонтальных каналов системы, определяемые по (9) по x₁, х₃, x₄, х₇, полученные на выходе первой ступени, а также переменные х₃, х₇, являющиеся (как это следует из (38), (39)) оценками ошибок построения вертикали. Эти переменные используются в качестве исходных параметров второй ступени для получения оценок корректируемой БИНС.

На графиках Фиг. 4-13 представлены результаты работы первой ступени. На графиках Фиг. 4 представлены невязки Z1-γ1, Z2-γ2, полученные при работе первой ступени. Асимптотическая сходимость этих переменных к нулю свидетельствует об устойчивости и наблюдаемости полученной системы. На графиках Фиг. 5 представлены оцениваемые параметры β₁, β₂ и разницы между этими параметрами и их оценками, определяющими точность оцениваемых параметров. На графиках Фиг. 6 представлены оцениваемые параметры α₁, α₂ и разницы между этими параметрами и их оценками. На графиках Фиг. 7-9 представлены измерения, параметры и разницы между этими параметрами и их оценками, аналогичные параметрам, представленным на графиках Фиг. 4-6, при ошибке β₃ = 10 угл. мин. На графиках Фиг. 10, 11 представлены параметры и разницы между этими параметрами и их оценками, аналогичные параметрам, представленным на графиках Фиг. 4-6 при инструментальных ошибках системы δω₁ = 0.1 угл. мин/мин. и δω₂ = 0.2 угл. мин/мин. На Фиг. 12,13 представлены параметры и разницы между этими параметрами и их оценками, аналогичные параметрам, представленным на графиках Фиг. 4-6, при центрированной позиционной случайной ошибке, равномерно распределенной в диапазоне ±0.5 угл. мин., и при нулевых инструментальных и курсовой ошибках системы. Графики Фиг. 7-13 показывают влияние таких ошибок системы, как курсовая ошибка, нескомпенсированные дрейфы по горизонтальным осям и случайная ошибка измерения позиции, на точность определяемых выходных параметров системы при сделанных выше допущениях.

Прежде всего, отметим, что поскольку выходными параметрами рассмотренной выше первой ступени являются элементы β₁, β₂ вектора β кинематических ошибок системы, то результат работы первой ступени можно рассматривать как результат визирования гипотетической звезды, находящейся в зените. Тогда, принимая это во внимание для определения всех трех компонент вектора β достаточно визирование одной звезды, что существенно облегчит получение необходимых для коррекции системы астропоправок. При этом матрица связи Н будет иметь вид:

где азимутальный угол А в первых двух строках матрицы Н может быть определен как:

Процедура определения третьей компоненты β₃ может быть еще более упрощена, если формировать вектор измерения, получаемый при визировании второй (реальной) звезды как алгебраическую сумму угловой поправки, получаемой в результате визирования второй звезды и оценок β₁, β₂ вектора β, получаемых на выходе первой ступени. Так, из четвертой строки (49) получаем:

откуда, сформировав вектор измерения:

где β₁,β₂ - выходные параметры первой ступени, получаем:

где:

В результате проделанных выкладок построим вторую ступень в виде линейного уравнения (50) первого порядка, выходом которого является оценка третьей компоненты β₃ вектора β кинематических ошибок системы.

Структурно блок-схема второй ступени, относящейся к блоку 13 (Фиг. 2) и входящей в состав представленной на Фиг. 3 трехступенчатой системы определения корректирующих поправок, включает подключенный к выходу седьмой разностной схемы 48 пятнадцатый усилитель 51 с коэффициентом усиления 1/CosB₂, шестнадцатый усилитель 52 с коэффициентом усиления 1/CosB₂, подключенный к выходу восьмой разностной схемы 49, семнадцатый усилитель 53 с коэффициентом усиления TgB₂CosA₂, подключенный к выходу блока 12 вычисления угловых поправок ΔА, ΔВ, а также седьмой сумматор 54, к которому подключены своими выходами усилители 51, 52 и 53. Во второй ступени определяется третья компонента β₃ вектора β кинематических ошибок системы в соответствии с (51), (52). Входными параметрами второй ступени являются получаемые в результате визирования звезды угловые поправки ΔА, ΔВ, вычисляемые в блоке 12, а также элементы β₁, β₂ вектора кинематических ошибок системы, получаемые на выходе первой ступени - разностных схем 48 и 49.

На графиках Фиг. 14 представлены кинематическая ошибка системы β₃ и разность между этой ошибкой и ее оценкой, полученной по (51), (52) при наличии азимутального дрейфа ν₃ = 0.1 град/час и при нулевых ошибках измерения, характеризующая точность получаемой по этому способу оценки. Большая ошибка получаемой оценки на первых 500 секундах вызвана переходным процессом при получении оценок β₁, β₂ на первой ступени. В установившемся состоянии ошибка оценки не превышает 0.8 угл. мин. На графиках Фиг. 15 представлены аналогичные результаты при наличии центрированной случайной позиционной ошибки измерения, распределенной по равномерному закону в диапазоне 0.1 угл. мин.

На выходе третьей ступени (блок 14) системы определения корректирующих поправок определяется вектор v некомпенсированных дрейфов системы.

Прежде чем приступать к построению третьей ступени, отметим, что перепроектирование векторов из системы координат, связанной с сопровождающим трехгранником, в систему координат, связанную с приборным трехгранником, и обратно осуществляется перемножением исходного вектора на матрицу ориентации А, либо на А^т, представляющую ортонормированную матрицу направляющих косинусов.

Дифференциируя (55), (56) с учетом уравнения Пуассона:

получаем:

Уравнение (56)получено транспонированием уравнения (55) Пуассона с учетом свойства кососимметрических матриц

Прежде чем строить наблюдаемое подпространство второй ступени докажем одно утверждение.

Лемма 1

Для кососимметрической матрицы

справедливо:

где:

(59), (60) доказывается непосредственно перемножением матриц:

Непосредственно из Леммы1 следует Теорема1:

Т е о р е м а 1

Для систем вида (48) с f(t)=Const имеет место тождество:

Утверждение доказывается непосредственным дифференцированием x(t). С учетом уравнения Пуассона:

Обозначив как и выше Ω1²+Ω2²+Ω3³=S², получим (63).

Т е о р е м а 2

Для алгебраических соотношений вида:

где: А – ортонормированная матрица, образуемая разворотом исходной системы координат (трехгранника) на три угла Эйлера (примером такой матрицы является матрица (1), справедливо:

Доказательство.

Дифференцируя (66), (67), из уравнений Пуассона получаем:

откуда, проведя два шага дифференцирования, получаем (69), (70), где вектор представляет проекции вектора инструментальных ошибок системы v на оси сопровождающего трехгранника

Обозначим вектор через y. Тогда:

и в соответствии с Теоремой 1, последовательно дифференцируя y, получаем:

Применим полученные результаты (Теорема 1) для построения наблюдаемого подпространства второй ступени.

Будем решать задачу определения векторов β и ν в проекциях на оси сопровождающего трехгранника, где в качестве базовых берутся кинематические уравнения (8) ошибок системы, записанные в проекциях на оси сопровождающего трехгранника.

Для построения наблюдаемого подпространства второй ступени введем переменные:

В новых переменных (8) запишется:

Тогда система (8) в новых переменных (76)-(80) с измерением z запишется

где:

x₁=β (83)

x₂=Aν (84)

Структура (84) совпадает с (75). Тогда, последовательно дифференцируя и вводя новые переменные, в соответствии с Теоремой 1 получаем:

где:

ω₁, ω₂, ω₃ - скорости вращения матрицы ориентации А (скорости изменения углов курса, крена и тангажа).

Тогда уравнение кинематических ошибок системы в матричном виде запишется, как:

где переходная матрица имеет блочный вид (каждый блок имеет размер 3×3):

где:

Е - единичная матрица размера 3×3;

dT - шаг интегрирования;

σ² - оп