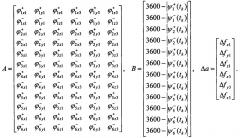Способ определения коэффициентов калибровки интегрированного блока датчиков

Способ определения коэффициентов калибровки интегрированного блока датчиков

Иллюстрации

Показать все

Реферат

Изобретение относится к области навигации, навигационных приборов, испытаний и калибровки и может быть использовано для калибровки датчиков бесплатформенных инерциальных систем ориентации и навигации летательных аппаратов, морских, наземных и других подвижных объектов. Интегрированный блок датчиков (ИБД) представляет собой вмонтированные в общий корпус тройку ортогонально расположенных датчиков угловых скоростей (ДУС) и тройку ортогональных датчиков линейных ускорений (ДЛУ), у которых соответствующие оси чувствительности коллинеарны. Эти блоки также называют инерциальными измерительными модулями (ИИМ).

Способ подразумевает уменьшение времени и трудоемкости процесса калибровки при увеличении точности определения коэффициентов калибровки и количества определяемых параметров калибровки инерциальных датчиков, что позволяет снизить требования к их характеристикам точности и стоимости. По этой причине повышение качества калибровки, при снижении трудоемкости процесса, было и остается актуальной проблемой.

Известен быстрый способ калибровки ИИМ [1]. В соответствии с данным способом, оператор вращает ИИМ во всех направлениях без внешнего оборудования либо с помощью оборудования. Снимаемые в это время с ИИМ данные позволяют определять 12 коэффициентов моделей погрешностей датчиков ИИМ, в том числе скорости дрейфов и масштабные коэффициенты ДУС, нулевые сигналы и масштабные коэффициенты акселерометров.

Недостатком данного способа является отсутствие среди оцениваемых коэффициентов модели ошибок калибруемых датчиков коэффициентов чувствительности. Определение этих коэффициентов особенно актуально для микромеханических ДУС, т.к. дрейфы, вызванные влиянием линейных ускорений на показания ДУС такого типа, могут достигать уровня 0.1 град/с и являются величинами одного порядка с нулевыми сигналами ДУС. Не включение данных коэффициентов в модель погрешностей ДУС приводит к неверному оцениванию нулевых сигналов ДУС.

Известен также способ калибровки ДУС в составе бесплатформенных инерциальных измерительных модулей (БИИМ) [2], при этом по сигналам двухкомпонентного ДУС и трех однокомпонентных акселерометров, т.е. блока акселерометров, входящих в состав БИИМ, калибруют коэффициенты модели угловой скорости дрейфа каждого ДУС, зависящего и не зависящего от линейных перегрузок, а также углы отклонений двух его осей чувствительности и оси кинетического момента от их номинальных направлений, материализуемых установочной плоскостью и базовым направлением на корпусе ДУС.

Суть способа состоит в том, что с помощью кронштейна и поворотной установки ИИМ устанавливают в трех различных фиксированных положениях по зенитному углу (Θ=0°; Θ=90°), при этом установку углов зенита производят по сигналам акселерометров и в каждом из них разворачивают ИИМ на азимутальные углы, близкие к значениям 0°, 90°, 180°, 270°. Во всех фиксированных положениях определяют сигналы ДУС по двум компонентам вектора измеряемой угловой скорости вращения Земли, запоминают их, а потом складывают и вычитают результаты одноименных измерений по каждому измеряемому компоненту угловой скорости и по соответствующим алгоритмам определяют коэффициенты моделей угловых скоростей дрейфа, а также углы неточной установки осей чувствительности и вектора кинетического момента ДУС. При этом сигналы блока акселерометров используются для определения угла зенита и угла установки отклонителя.

Недостатком данного способа является то, что он не обеспечивает режимы калибровки масштабных коэффициентов, не полностью обеспечивает определение углов неточной установки измерительных осей однокомпонентных ДУС на основе волоконно-оптических, волновых твердотельных и других гироскопов, трех акселерометров, а также не позволяет определять углы не параллельности соответствующих одноименных измерительных осей ДУС и акселерометров.

Выбранный нами в качестве прототипа является способ калибровки датчиков угловой скорости бесплатформенного ИИМ [3], реализованный в известном широкодиапазонном стенде (например, УПГ-48), обеспечивающем приблизительно горизонтальное задание вектора угловой скорости с фиксированным направлением в пространстве. С помощью стендового оборудования вращают ИИМ последовательно вокруг трех приблизительно ортогональных осей ИИМ. Во время вращения записывают показания ИИМ по каналу акселерометров, показания ДУС. По сигналам акселерометров определяют угловую скорость ИИМ в базисе акселерометров. Идентифицируя математическую модель ДУС, определяют нулевые сигналы ДУС, матрицу, описывающую масштабные коэффициенты, перекрестные связи, ориентацию осей чувствительности ДУС в ИИМ, матрицу, описывающую влияние линейного ускорения на показания ДУС.

Недостатками данного способа являются:

- необходимость предварительной калибровки акселерометров и переустановки ИИМ на платформе,

- определение вектора угловой скорости вращения ИИМ по сигналам акселерометров посредством формирования разделенной разности оценок углов ориентации ИИМ на соседних тактах их опроса, т.е. численного дифференцирования сигналов акселерометров, что приводит к высокой интенсивности случайной составляющей в формируемых оценках, принимаемых в данном способе калибровки датчиков угловой скорости за входное воздействие. Это значительно ограничивает достижимую точность калибровки.

Целью изобретения является повышение точности калибровки, сокращение трудозатрат и времени калибровки за счет автоматизации процесса калибровки и применения уточненной модели погрешности при не высоких требованиях к используемой аппаратуре, а также осуществление контроля правильности калибровки.

Поставленная цель достигается за счет того, что согласно заявленному способу определения коэффициентов калибровки интегрированного блока датчиков (ИБД), включающий вращение с помощью стендового оборудования последовательно как минимум по двум непараллельным осям в базисе калибруемого ИБД, во время вращения записывают показания ИБД по каналу датчиков линейного ускорения (ДЛУ), показания датчиков угловой скорости (ДУС), идентифицируя математическую модель ДУС, определяют нулевые сигналы ДУС, матрицу, описывающую масштабные коэффициенты, перекрестные связи, дополнительно осуществляют вращение ИБД по заданному количеству 10 оборотов с выбегом, чтобы этапы разгона и торможения можно было исключить из массивов измерений, в диапазоне угловых скоростей ±0.5, ±2.5, ±10, ±40, ±120, ±240 градусов в секунду по трем осям внутренней связанной системы координат датчиков ИБД, исключают этапы разгона и торможения из измерений, образуют при этом массивы данных показаний ДУС и ДЛУ с постоянной частотой, например 100 Гц, на каждое вращение, путем специальной обработки полученной переопределенной системы, используя методы статистической обработки, осуществляют определение линейных приближений масштабных коэффициентов, уточнение масштабных коэффициентов с учетом асимметрии, определение нелинейной зависимости масштабных коэффициентов от скорости вращения в виде узлов интерполяции, общих для множества скоростей вращения, определение коэффициентов чувствительности и определение коэффициентов неортогональности осей чувствительности датчиков, причем проверка правильности определения коэффициентов калибровки может быть проведена после каждого этапа путем произвольного перемещения и вращения блока, и возврата в исходное состояние.

Суть способа определения коэффициентов калибровки ИБД, использующий полученные числовые массивы путем проведения 12 вращательных экспериментов и измерений сигналов в статическом положении, излагается ниже.

1. Расчет коэффициентов калибровки ДУС

Коэффициенты калибровки ДУС определяют поэтапно. Число этапов расчета определяется сложностью модели ошибок датчиков. Рассматривают следующие этапы определения статических характеристик ДУС:

- определение постоянных ошибок (смещений нуля);

- определение линейных приближений масштабных коэффициентов;

- уточнение масштабных коэффициентов с учетом асимметрии;

- уточнение нелинейности масштабных коэффициентов;

- определение коэффициентов неортогональности;

1.1 Определение постоянных ошибок

Используют измерения 12 экспериментов на начальных участках, соответствующих статическому положению блока (без вращения). Измерения в кодовых единицах подвергаются предварительному масштабированию.

Обозначим - измеренные угловые скорости в кодовых единицах. По каждому из трех процессов измерений выполняются следующие расчеты:

здесь Cod (ω') - код измеренного сигнала от аналого-цифрового преобразователя датчика;

С₀ - смещение нуля в единицах младшего разряда кода, вычисляемое при спокойном положении стола;

М(ω) - зависимость масштабного коэффициента датчика от угловой скорости вращения стола;

ω^* - результирующее значение угловой скорости [град./с].

1. Из кодов 12 экспериментов измерений нулевых значений угловых скоростей длительностью 2,5 минуты вычитают константы 2¹⁵=32768.

2. Полученные значения делят на 2¹⁰=1024 и представляют в вещественном формате.

3. Вычисляют оценки математических ожиданий (средние арифметические значения) для каждого из 12 экспериментов C_0i, i=1, …, 12.

4. Оценки C_0i, i=1, …, 12 усредняют по 12 экспериментам, полученное значение является оценкой постоянной ошибки датчика С₀.

5. Контроль точности. Вычисляют среднеквадратическое отклонение (СКО) оценок C_0i, i=1, …, 12 по 12 экспериментам σ(С₀).

Вычисляют коэффициент относительной точности оценки постоянной ошибки

, где N=12.

6. Дополнительный контроль качества сигналов. Строятся гистограммы распределения центрированных сигналов:

С помощью гистограмм оценивают качество измерений нулевых сигналов. Хорошее качество измерений соответствует симметричному закону распределения, в котором практически все измерения находятся в диапазоне трех СКО. Результатом данного этапа являются три постоянные ошибки C_0x, C_0y, C_0z и три коэффициента относительной точности их оценки α_x, α_y, α_z.

1.2. Определение линейных приближений масштабных коэффициентов

Линейная статическая характеристика (математическая модель) датчика содержит два коэффициента, один из которых (постоянная ошибка) определен на предыдущем этапе. На данном этапе для каждого датчика рассчитывают масштабный коэффициент, определяющий угол наклона линейной статической характеристики. Коэффициенты определяют на основании информации о полном (конечном) обороте поворота стола в плоскости его вращения.

Из экспериментов 1-6 выбирают участки вращения от исходного статического положения блока до его полной остановки, содержащие 10 полных оборотов, по 2 участка для каждого эксперимента, соответствующие вращению в одну и другую сторону. Всего выбирают 12 участков измерений, по 2 для каждого эксперимента. Длительность участков больше времени вращения, так как учитывается разгон и торможение стола. Последовательность расчетов аналогична п. 1.1, с тем отличием, что теперь определяют шесть ординат - по две ординаты для каждого датчика.

Последовательность расчетов следующая. Для каждого датчика назначают вспомогательную систему координат, необходимую для вычисления угла поворота стола по уравнениям Эйлера. Для экспериментов №1, 2 (вращение вокруг оси x) исходную систему координат блока xyz заменяют на вспомогательную систему y₁x₁z₁:

Для экспериментов №3, 4 (вращение вокруг оси y) вспомогательная система координат y₁x₁z₁ совпадает с исходной системой xyz:

Для экспериментов №5, 6 (вращение вокруг оси z) исходную систему координат xyz заменяют на вспомогательную систему x₁z₁y₁:

При вычислении конечных углов поворота используют измерения во вспомогательных осях ω_x1, ω_y1, ω_z1. Оценка конечных углов поворота по измерениям зависит от искомых масштабных коэффициентов, поэтому процесс их определения является итерационным. Для универсальности методики расчета, которую далее распространяют на нелинейные характеристики датчиков, идентифицируют не сами масштабные коэффициенты, а ординаты узлов линейной интерполяции статических характеристик которые потом пересчитывают в масштабные коэффициенты. Последовательность расчетов следующая:

1. Задают абсциссы трех узлов интерполяции {u_x1, u_x2, u_x3}={u_y1, u_y2, u_y3}={u_z1, u_z2, u_z3}={-40, 0, 40} и начальные приближения их трех ординат , одинаковые для всех трех характеристик.

Так как для линейной статической характеристики имеет место , то идентификации подлежат три коэффициента, по одному коэффициенту для каждого датчика

Обозначим интерполированные угловые скорости:

Оценка угла полного поворота стола равна конечному значению угла ψ(t_k), вычисленного интегрированием уравнений Эйлера, где t_k - время окончания вращения стола:

При решении уравнений (2) в них подставляют интерполированные угловые скорости (1). Обозначим - значения конечного угла поворота стола при положительном и при отрицательном направлении его вращения соответственно. Эти величины используют далее для определения масштабных коэффициентов.

2. Определение коэффициентов чувствительности.

2.1. Уравнения (2) решают 12 раз на отрезках времени для выбранных 12 участков вращения стола с целью определения очередных приближений масштабных коэффициентов и определения 12 оценок конечного угла поворота:

Обозначим и - коэффициенты чувствительности конечного угла поворота при положительном направлении и отрицательном направлении вращения стола к изменению ординаты статической характеристики . В данном случае с учетом линейности характеристик n=1. Аналогичные обозначения вводятся и для датчиков ω_y, ω_z.

2.2. Уравнения (2) решают 12 раз при приращении ординаты на величину . При этом определяют приращения оценок конечных углов поворота относительно их значений (3) и 12 коэффициентов чувствительности , m=1, 2, … 6.

2.3. Уравнения (2) решают 12 раз при приращении ординаты на величину Определяют приращения оценок конечных углов поворота относительно их значений (3) и 12 коэффициентов чувствительности , m=1, 2, … 6.

2.4. Уравнения (2) решают 12 раз при приращении ординаты на величину . При этом определяют приращения оценок конечных углов поворота относительно их значений (3) и 12 коэффициентов чувствительности , m=1, 2, …6.

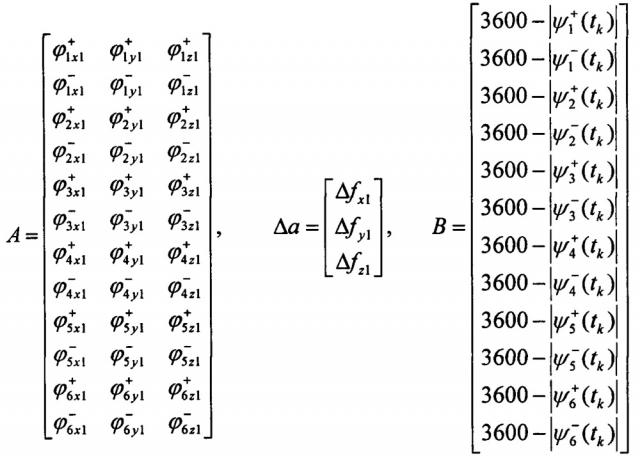
3. Формируют переопределенную систему линейных алгебраических уравнений для приращений оценок искомых масштабных коэффициентов относительно их приближений:

Здесь А - матрица коэффициентов чувствительности размерности 12×3, a - вектор искомых ординат ; Δa - вектор приращений относительно их приближений, ; В - вектор разностей между известными значениями конечных углов поворота и их оценками, полученными интегрированием уравнений (2)

4. Система уравнений (4) решается методом наименьших квадратов:

5. Определяются новые приближения вектора искомых ординат

где j - номер итерации, r=0.95 - коэффициент, улучшающий сходимость итерационного процесса.

6. Проверяется условие окончания итераций. Вычисляется сумма абсолютных значений приращений

При ε≥0.001 вычисления повторяются, начиная с п. 2. Достаточное число итераций - 7.

7. Рассчитываются коэффициенты наклона статических характеристик:

8. Формулы вычисления величин угловых скоростей в единицах измерения [град/с] по кодам сигналов датчиков имеют вид:

Или:

, где: M_x=K_x/1024,

, где: M_y=K_y/1024,

, где: M_z=K_z/1024,

где М_х, M_y, M_z - искомые линейные приближения масштабных коэффициентов.

9. Контроль правильности калибровки.

Для контроля используются все 12 экспериментов, а также дополнительные эксперименты, при которых выполняется произвольное перемещение и вращение блока с возвратом в исходное состояние.

9.1. Контроль по 12 экспериментам на столе заключается в вычислении 24 конечных углов поворота вокруг вспомогательной оси блока y₁, которые должны составлять 3600 градусов, независимо от наклона блока. При этом вспомогательные оси назначаются следующим образом.

Для экспериментов №1, 2, 11-12 исходная система координат блока xyz заменяется на вспомогательную систему y₁x₁z₁.

Для экспериментов №3, 4 вспомогательная система координат y₁x₁z₁ совпадает с исходной системой xyz.

Для экспериментов №5, 6 (вращение вокруг оси z) исходная система координат xyz заменяется на вспомогательную систему x₁z₁y₁.

Для экспериментов №7-10 исходная система координат xyz заменяется на вспомогательную систему z₁x₁y₁.

Вычисляется среднее значение модуля ошибки конечных углов поворота по 24 участкам.

9.2. Контроль по экспериментам с произвольным перемещением и вращением блока и возвратом в исходное состояние выполняется решением уравнений (2) с нулевыми начальными условиями в течение всего эксперимента.

При этом следует не допускать выхода сигналов датчиков на ограничения по диапазонам измерения. Вспомогательные оси следует выбирать так, чтобы начальный угол тангажа блока был равен нулю. Контроль выполняют по отклонению конечных углов поворота от нулевых значений.

1.3. Уточнение масштабных коэффициентов с учетом асимметрии

Нелинейная статическая характеристика датчика, учитывающая асимметрию масштабного коэффициента, содержит три коэффициента, один из которых (постоянная ошибка) определен ранее.

Используют участки вращения блока в экспериментах 1-6 с учетом разгона и торможения стола до полной остановки.

Последовательность расчетов аналогична п. 1.2, с тем отличием, что теперь определяется шесть ординат - по две для каждого датчика. Последовательность расчетов следующая.

1. Задают абсциссы трех узлов интерполяции {u_x1 u_x2, u_x3}={u_y1, u_y2, u_y3}={u_z1, u_z2, u_z3}={-40, 0, 40} и начальные приближения их трех ординат , вычисленные для линейных приближений масштабных коэффициентов.

2. Определение коэффициентов чувствительности.

2.1. Уравнения (2) решают 12 раз на отрезках времени выбранных 12 участков вращения стола для приближений масштабных коэффициентов и определяются 12 оценок конечного угла поворота. При этом в уравнения Эйлера подставляют интерполированные значения угловых скоростей. Определяют оценки конечных углов поворота блока.

2.2. Уравнения (2) решают 12 раз при приращении ординаты на величину

Определяют приращения оценок конечных углов поворота относительно их значений (9) и 12 коэффициентов чувствительности

, m=1, 2, …6.

2.3. Уравнения (2) решают 12 раз при приращении ординаты на величину

Определяют приращения оценок конечных углов поворота относительно их значений (9) и 12 коэффициентов чувствительности

, m=1, 2, …6.

2.4. Уравнения (1) решают 12 раз при приращении ординаты на величину

Определяют приращения оценок конечных углов поворота относительно их значений (9) и 12 коэффициентов чувствительности

, m=1, 2, …6.

2.5. Уравнения (1) решают 12 раз при приращении ординаты на величину

Определяют приращения оценок конечных углов поворота относительно их значений (9) и 12 коэффициентов чувствительности

, m=1, 2, …6.

2.6. Уравнения (1) решают 12 раз при приращении ординаты на величину

Определяют приращения оценок конечных углов поворота относительно их значений (9) и 12 коэффициентов чувствительности

, m=1, 2, …6

2.7. Уравнения (1) решают 12 раз при приращении ординаты на величину

Определяют приращения оценок конечных углов поворота относительно их значений (9) и 12 коэффициентов чувствительности

, m=1, 2, …6.

3. Формируют переопределенную систему линейных алгебраических уравнений для приращений оценок искомых масштабных коэффициентов , относительно их приближений.

AΔа=В,

здесь А - матрица коэффициентов чувствительности размерности 12×6, а - вектор искомых ординат ; Δа - вектор приращений относительно их приближений ; В - вектор разностей между известными значениями конечных углов поворота и их оценками, полученными интегрированием уравнений (2)

4. Систему уравнений (3) решают методом наименьших квадратов:

5. Определяют новые приближения вектора искомых ординат:

a _j+1=a_j+rΔа, где j - номер итерации, r=0.75 - коэффициент, улучшающий сходимость итерационного процесса.

6. Проверяют условие окончания итераций. Для контроля сходимости итерационного процесса вычисляют сумму абсолютных значений приращений:

При ε≥0.001 вычисления повторяются, начиная с п. 2. Достаточное число итераций - 10.

7. Рассчитывают коэффициенты наклона отрицательной и положительной ветвей статических характеристик

8. Формулы вычисления величин угловых скоростей в единицах измерения [град/с] по кодам сигналов датчиков имеют вид

при

при , где

при

при , где

при

при , где

9. Контроль правильности калибровки.

Для контроля используют все 12 экспериментов, а также дополнительные эксперименты, при которых выполняют произвольное перемещение и вращение блока с возвратом в исходное состояние. Контроль выполняют по конечным углам поворота, аналогично тому, как это делается при определении линейных приближений масштабных коэффициентов.

1.4. Уточнение нелинейности масштабных коэффициентов

Нелинейность статических характеристик учитывают путем наращивания числа узлов кусочно-линейной интерполяции. При этом используют дополнительные эксперименты с повышенной скоростью вращения стола.

Рассмотрим случай, когда статические характеристики содержат по 5 узлов интерполяции, то есть добавляется по два узла к характеристикам, определенным в п. 1.3. При этом эксперименты 1-6 повторяются при скорости вращения стола, на которой ожидается проявление нелинейных свойств датчиков. Задаются значения угловых скоростей, при которых ожидается изменение угла наклона характеристик датчиков относительно их линейных приближений

Задаются максимальные значения угловых скоростей, достигаемые в экспериментах с повышенными угловыми скоростями .

Суть учета нелинейностей датчиков заключается в том, что при угловых скоростях, превышающих , значения масштабных коэффициентов изменяются. Узлы интерполяции статической характеристики датчика ω_х определяются заданием ординат и абсцисс пяти узлов интерполяции с учетом коэффициентов, определенных в п. 1.3:

:

Для датчиков ω_y, ω_z узлы интерполяции задаются аналогично.

Узлы 2-4 замораживают, а ординаты узлов 1,5 определяют указанным в п. 1.3 итерационным способом при использовании экспериментов с большими угловыми скоростями и с учетом числа оборотов, имеющих место в этих экспериментах. Всего определяют 6 ординат, по две для каждого датчика. Поэтому структура матриц аналогична рассмотренной в п. 1.3.

При необходимости значения могут быть уточнены варьированием в меньшую или большую сторону так, чтобы достичь максимальной точности воспроизведения конечных углов поворота блока.

Усложнение нелинейных статических характеристик достигается путем наращивания числа узлов интерполяции с привлечением экспериментов с все большими угловыми скоростями вращения стола. При этом на каждом этапе выполняется определение очередной пары ординат узлов интерполяции при замораживании узлов, найденных на этапах с меньшими угловыми скоростями. Поэтапное наращивание сложности описания нелинейных статических характеристик датчиков обеспечивает устойчивое решение задачи идентификации. Всякий раз определяется всего 6 коэффициентов, для которых достаточно информации во вновь привлекаемых данных, потому что если нелинейность не проявляется, то не производится попытка определения нулевых значений, как это было бы при использовании степенных или иных полиномов, а выполняется подтверждение найденных ранее масштабных коэффициентов для меньших угловых скоростей. Кроме того, поэтапное определение узлов интерполяции позволяет контролировать процесс их уточнения с привлечением новых экспериментальных данных.

Вычисление оценок угловых скоростей выполняют с учетом попадания текущих значений сигналов в соответствующие диапазоны кусочно-линейной интерполяции и значений масштабных коэффициентов для этих диапазонов.

1.5. Определение коэффициентов неортогональности

Коэффициенты неортогональности (взаимного влияния) сигналов ДУС рассчитывают после определения масштабных коэффициентов. Для этого из измерений экспериментов 1-6 выделяют участки вращения с постоянной угловой скоростью, исключая разгон и торможение стола. Затем вычисляют средние значения и сигналов ω_х, ω_y, ω_z, для каждого эксперимента, соответствующие положительному и отрицательному направлению вращения стола, где m=1, 2, …6 - номер эксперимента.

1. Коэффициенты влияния сигнала ω_х, на сигналы ДУС ω_y, ω_z:

где

2. Коэффициенты влияния сигнала ω_y на сигналы ДУС ω_x, ω_z:

где

3. Коэффициенты влияния сигнала ω_z, на сигналы ДУС ω_х, ω_y:

где

4. Оценки угловых скоростей с учетом коэффициентов взаимного влияния определяют соотношениями:

где ω_х, ω_y, ω_z - оценки угловых скоростей, вычисленные в п. 1.3.

2. Расчет коэффициентов калибровки ДЛУ

Коэффициенты калибровки ДЛУ определяют по линейной модели ошибок совместно за один прием по начальным участкам 12 экспериментов, соответствующих статическим положениям блока. Для расчета коэффициентов калибровки используется ускорение земного притяжения. При статическом положении блока модуль ускорения земного притяжения, компоненты которого измеряются датчиками , независимо от положения блока равен единице (в единицах перегрузки).

Обозначим - вектор измерений соответствующих ДЛУ. Измерения перегрузок в кодовых единицах подвергают предварительному масштабированию и представлению в вещественном формате:

Обозначим - вектор перегрузок, рассчитываемых при калибровке.

Линейная модель ошибок ДЛУ, записанная в матричном виде, имеет вид:

Здесь С - матрица масштабных коэффициентов.

- вектор постоянных ошибок размерности 3×1.

С учетом равенства модуля перегрузки единице имеет место соотношение

Соотношение (12) может быть представлено в виде следа матрицы , размерность которой равна 3×3

Для множества измерений одного эксперимента, содержащего N отсчетов , имеет место скалярное равенство

При подстановке (11) в (14) и учитывая постоянство элементов матриц С, С₀, имеет место соотношение

где

Здесь - матрица размерности 3×3; - вектор размерности 3×1.

При учете множества экспериментов из М=12 с разными положениями блока, каждый из которых содержит N отсчетов измерений, имеет место переопределенная система уравнений, состоящая из М уравнений вида (14), число которых равно числу экспериментов

где указывает принадлежность к эксперименту с номером .

Перекрестные члены матрицы С являются зависимыми, так как они определяются тремя углами межу осями чувствительности датчиков блока и тремя масштабными коэффициентами С_хх, С_уу, C_zz. Поэтому в матрице С имеются шесть независимых переменных, которыми являются элементы С_хх, C_yy, C_zz, C_xy, C_xz, C_yz. Остальные три элемента связаны с шестью указанными соотношениями:

Всего в матрицах С, С₀ присутствует девять независимых коэффициентов C_xx, C_yy, C_zz, C_xy, C_xz, C_yz, С_0х, C_0y, C_0z, процесс определения которых является итерационным. Последовательность расчетов следующая.

1. Предварительное масштабирование кодов 12 процессов измерений перегрузок стат