Триангуляционный метод измерения площади участков поверхности внутренних полостей объектов известной формы

Триангуляционный метод измерения площади участков поверхности внутренних полостей объектов известной формы

Иллюстрации

Показать все

Реферат

Изобретение относится к технологиям визуально-измерительного контроля (ВИК), позволяющим по зарегистрированным изображениям обнаружить искомые элементы поверхности контролируемых объектов в труднодоступных внутренних полостях различных технических устройств и сооружений и измерить геометрические характеристики этих элементов.

В ряде случаев, например, при контроле авиационных и ракетных двигателей, трубопроводов, теплообменников и других промышленных объектов, в ходе ВИК возникает необходимость не только выявить дефекты, но и измерить их геометрические характеристики [Клюев В.В., Соснин Ф.Р. Неразрушающий контроль. Справочник. Т. 1. Книга 1. Визуальный и измерительный контроль. // М.: Машиностроение, 2008, 324 с.]. Допустимость или недопустимость обнаруженных дефектов определяется требованиями нормативной документации к их геометрическим параметрам: поперечным размерам, глубине/высоте, площади и др., - различных для разных задач и видов дефектов. Одним из ключевых показателей является площадь дефекта, поскольку полезные характеристики изделия, определяемые рабочей площадью, в этом случае уменьшаются на соответствующую величину, а в некоторых случаях сама работоспособность и надежность работы этих изделий резко зависит от относительной площади дефектов.

Очевидно, что для принятия решения необходимо не только измерить геометрические размеры обнаруженного дефекта, но и оценить точность (погрешность) измерения. Поэтому вычисление и контроль погрешности подобных измерений является важной процедурой для обеспечения метрологической достоверности получаемых результатов [Savio Е., De Chiffre L. and Schmitt R. Metrology of freeform shaped parts. CIRP Annals - Manufacturing Technology, vol. 53/2, pp. 810-835, 2007].

Известны методы измерения геометрических характеристик объекта по сопоставлению нескольких его изображений, полученных одновременно с разных ракурсов при помощи нескольких устройств регистрации, с учетом информации о взаимном расположении этих устройств [Pears N., Liu Y. and Bunting P. 3D imaging, analysis and applications. London, UK: Springer Verlag, 2012. 500 p. Chapter 2, pp. 35-94]. В разных вариантах в этих методах может использоваться составная оптическая система (ОС), содержащая несколько пространственно разнесенных частей, и/или изображения, полученные синхронно с разных ракурсов, могут регистрироваться на разные части одного матричного приемника излучения (МПИ). При этом указанные устройства регистрации или отдельные части составной оптической системы жестко фиксируются, а их положение в пространстве измеряется перед началом измерений [ С. 3D computer vision. Efficient methods and applications. 2nd ed. London, UK: Springer Verlag, 2013. 382 p. Chapter 1.4, pp. 17-61]. Такие стереоскопические методы, называемые также фотограмметрией, относят к пассивным методам.

В этих методах сопоставление зарегистрированных изображений (снимков) дает возможность найти на них соответствующие точки, являющиеся проекциями какой-то точки объекта на плоскости снимков. Измерение координат точек на снимке производится либо оператором, либо автоматически при помощи программ обработки изображений. По координатам проекций на нескольких снимках вычисляются трехмерные координаты соответствующей им точки объекта (образа) с использованием данных о взаимном расположении устройств регистрации [Pears N., Liu Y. and Bunting P. 3D imaging, analysis and applications. London, UK: Springer Verlag, 2012. 500 p. Chapter 2, pp. 35-94]. Эти координаты определяют положение найденного образа точки, который может не совпадать с положением исходной точки объекта (прообраза) в пределах, определяемых погрешностью метода.

Эти стереоскопические методы позволяют эффективно решать задачи измерения площади тех участков поверхности объекта, которые выражены только текстурными признаками, практически не меняющими рельефа самой поверхности. К этому классу задач относится диагностика многих видов дефектов, подлежащих обнаружению и измерению при ВИК.

Площадь участка поверхности в этих методах определяется триангуляционным способом - путем разбиения участка на треугольники, вершины которых лежат на кривой линии, ограничивающей выделенный участок поверхности, - ее границе. Выделение границы участка на изображениях производится либо оператором, либо автоматически при помощи программы обработки изображений и представляется в виде последовательности граничных точек. Пространственные координаты образов этих точек, которые выбираются вершинами треугольников, вычисляются независимо друг от друга по координатам их проекций на плоскость снимков [http://www.ge-mcs.com/download/RVI/XLG3/GEIT-65015EN_measurement.pdf].

К недостаткам стереоскопических методов, ограничивающих их область применения, относится сложность или даже невозможность измерения пространственных координат участков поверхности, в окрестности которых отсутствуют ярко выраженные текстурные признаки. Также ввиду специфической особенности стереоскопических методов, состоящей в квадратичной зависимости погрешности измерения расстояния до исследуемого участка поверхности, погрешность измерения может быть существенной уже на небольших расстояниях от поверхности. Кроме того, погрешность измерений значительно возрастает при недостаточной освещенности объекта, при значительных искажениях изображения оптических регистрирующих систем, при наличии шума или помех на изображении [Pears N., Liu Y. and Bunting P. 3D imaging, analysis and applications. London, UK: Springer Verlag, 2012. 500 p. Chapter 2, pp. 35-94; Hirschmuller H. and Scharstein D. Evaluation of cost functions for stereo matching // Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR '07). 17-22 June 2007, Minneapolis, MN, USA. P. 1-8].

Еще одним недостатком описанных методов, сказывающимся на точности измерений, является то, что при значительной кривизне исследуемой поверхности или больших размерах измеряемого участка его площадь может заметно отличаться от площади поверхности, натянутой на замкнутую кривую, образующую его видимую границу [Горевой А.В., Мачихин А.С., Перфилов А.М. Определение погрешности бесконтактного измерения площади дефектов на поверхностях сложной формы при видеоэндоскопическом контроле // Научно-технический вестник информационных технологий, механики и оптики. 2014. №4 (92). С. 140-148]. Т.е. вышеописанный триангуляционный метод даже при предельно мелком разбиении позволяет определить лишь минимально возможную площадь поверхности, ограниченной заданным граничным контуром, и таким образом дает заниженную оценку площади. А конечное число выбираемых граничных точек дает еще одну составляющую погрешности. Этот недостаток становится существенным, когда все остальные составляющие погрешности минимизированы.

Для устранения этого недостатка следует знать или определить точную форму исследуемого участка поверхности, для чего необходимо найти образы точек, расположенных внутри границы. После этого можно провести триангуляцию по трехмерной поверхности участка. При этом плотность расположения точек определяет точность вычисления площади триангуляционным методом.

Известны методы, позволяющие определять форму поверхности объекта непосредственно в ходе измерений. К таким методам относятся, в частности, активные методы, использующие структурированную подсветку объекта, и дальнометрические методы, измеряющие время прохождения излучения до объекта [Savio Е., De Chiffre L. and Schmitt R. Metrology of freeform shaped parts. CIRP Annals - Manufacturing Technology, vol. 53/2, pp. 810-835, 2007, Pears N., Liu Y. and Bunting P. 3D imaging, analysis and applications. London, UK: Springer Verlag, 2012. 500 p. Chapter 3, pp. 95-138]. Эти методы не требуют наличия ярко выраженных текстурных признаков и позволяют получить плотную сетку точек поверхности объекта с вычисленными/измеренными трехмерными координатами, что позволяет не только определить взаимное положение и ориентацию системы регистрации относительно объекта, но и измерить отклонения измеряемого объекта от эталонной трехмерной модели в тех случаях, когда эта модель известна, а также провести измерения площади выделенного участка поверхности объекта с высокой точностью [http://www.ge-mcs.com/download/RVI/XLG3/tech-paper-3d-measurement.pdf; https://www.karlstorz.com/cps/rde/xbcr/karlstorz_assets/ASSETS/3217790.pdf]. Однако применение этих методов для ВИК внутренних полостей реальных промышленных объектов ограничено, поскольку этот вид инспекции требует, как правило, весьма малых габаритов регистрирующей системы для доставки ее в исследуемую внутреннюю полость через специализированные отверстия диаметром несколько миллиметров. Зачастую этот вид ВИК требует и высокой скорости регистрации, что затруднительно реализовать такими достаточно сложными техническими устройствами.

В рассмотренных пассивных, стереоскопических методах в отсутствие ярко выраженных текстурных признаков отождествить внутренние точки крайне затруднительно в отличие от граничных точек, лежащих на стыке двух контрастно различающихся областей. А потому в этих методах необходимо использовать дополнительную информацию о форме поверхности, априорную или получаемую в ходе предварительных измерений.

При решении многих задач ВИК имеется трехмерная модель объекта или чертеж, достаточный для ее построения, и эта информация может быть эффективно использована для решения вышеуказанной проблемы учета формы поверхности. Если знать или вычислить положение и ориентацию объекта относительно системы регистрации, то можно установить однозначное соответствие между координатами точек на изображениях и их образами, располагаемыми на поверхности, описываемой моделью объекта. Привязка образов точек к поверхности известной формы позволит значительно снизить погрешность определения их трехмерных координат, учесть кривизну поверхности и, следовательно, заметно снизить погрешность вычисления площади [Горевой А.В., Мачихин А.С., Перфилов A.M. Определение погрешности бесконтактного измерения площади дефектов на поверхностях сложной формы при видеоэндоскопическом контроле // Научно-технический вестник информационных технологий, механики и оптики. 2014. №4 (92). С. 140-148].

Определить положение и ориентацию системы регистрации позволяют вышеописанные стереоскопические методы, а в случае известной трехмерной структуры объекта эта точность возрастает [ С. 3D computer vision. Efficient methods and applications. 2nd ed. London, UK: Springer Verlag, 2013. 382 p. Chapter 1.6, pp. 87-126; Pauwels K., Rubio L., Diaz J. and Ros E. Real-time model-based rigid object pose estimation and tracking combining dense and sparse visual cues // Proceedings of 2013 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 23-28 June 2013, Portland, OR, USA. P. 2347-2354]. В этом случае при установлении соответствия между координатами точек на снимках и их образами, принадлежащими поверхности известной формы, координаты системы регистрации (положение и ориентация) являются свободными параметрами. Тем не менее, вследствие сильной чувствительности этих методов к различным факторам (расстояние до объекта, освещенность, аберрации) эта точность может быть недостаточна. Более того, в случае, когда все изображение занимает участок однородной поверхности, проблема нахождения образов внутренних точек участка делает учет кривизны поверхности практически невозможным.

Есть пассивные методы, позволяющие инструментально контролировать положение системы регистрации и для объектов с известной трехмерной структурой осуществлять ВИК посредством видеокамеры, используя изображение, полученное с одного ракурса [ С. 3D computer vision. Efficient methods and applications. 2nd ed. London, UK: Springer Verlag, 2013. 382 p. Chapter 1.6, pp. 87-126; С 3D computer vision. Efficient methods and applications. 2nd ed. London, UK: Springer Verlag, 2013. 382 p. Chapter 4.5, pp. 230-240].

Например, при проведении ВИК внутренней полости объекта используют устройства позиционирования (механические датчики и приспособления, оптические или лазерные трекеры), позволяющие определить положение и ориентацию зонда относительно некоторой базовой поверхности объекта: [Savio Е., De Chiffre L. and Schmitt R. Metrology of freeform shaped parts. CIRP Annals - Manufacturing Technology, vol. 53/2, pp. 810-835, 2007]. Объекты известной формы, представляющие зачастую изделия машиностроения, как правило, имеют участок плоской поверхности, которая может служить надежной опорой для контрольно-измерительной аппаратуры.

Взаимное положение и ориентация регистрирующей системы и участка поверхности вычисляются из совокупности данных, включающих координаты проекций точек на снимках, трехмерной модели объекта и координаты системы регистрации. Для часто встречающихся случаев, когда все изображение занимает участок гладкой поверхности, эти методы не применимы. Но и в тех случаях, когда исследуемый участок поверхности объекта имеет текстуру, точность определения соответствия точек на снимке и на трехмерной модели может оказаться недостаточной.

Хотя при использовании устройства позиционирования формально имеется полная информация о положении регистрирующей системы, фактически информация об ориентации системы обычно недостаточно надежна. Это связано с тем, что даже небольшая неопределенность угла ориентации Δϕ при заметном удалении от исследуемой поверхности R приводит к большой погрешности в координатах точки поверхности Δх=R⋅Δϕ. Эта неточность присутствует в вышеописанных пассивных методах: стереоскопическом и одноракурсном с использованием устройства позиционирования.

В нижеописанном новом методе, основанном на стереоскопической регистрации с использованием устройства позиционирования, избыточная информация позволяет устранить эту ориентационную составляющую погрешности и существенно уменьшить суммарную погрешность. И в этом случае для правильной оценки точности измерения уже становится необходимым учет кривизны поверхности. Кроме того, определение образов внутренних точек участка поверхности позволяет оценить возможную деформацию участка по сравнению с известной по чертежам начальной формой.

Задачей изобретения является устранение недостатков стереоскопического метода при измерении площадей участков поверхности сложной формы.

Техническим результатом изобретения является повышение объективности контроля за счет снижения погрешности измерений площадей участков поверхности сложной формы триангуляционными методами.

Указанный технический результат достигается за счет того, что в стереоскопическом методе измерений площади участков поверхности внутренних полостей объектов известной формы, заключающемся в контролируемом перемещении системы регистрации изображений относительно базовой поверхности объекта, записи в цифровом виде нескольких изображений поверхности объекта с различных ракурсов при помощи системы регистрации, сопоставлении синхронно записанных изображений, обнаружении на них искомых участков поверхности и выделении границ этих участков в виде последовательности граничных точек на замкнутой кривой, определении положения пространственного образа граничных точек и вычислении путем триангуляции площади поверхности, натянутой на пространственный образ границы, одновременно с записью изображений осуществляют измерение положения и ориентации системы регистрации относительно базовой поверхности объекта, задают множество опорных точек изображения внутри границы, плотность расположения которых определяется требуемой точностью измерений, определяют положение их пространственных образов с учетом их расположения на поверхности, имеющей локальную форму объекта, вычисляют путем триангуляции площадь выделенного участка этой поверхности с использованием как точек на границе, так и дополнительно заданных точек.

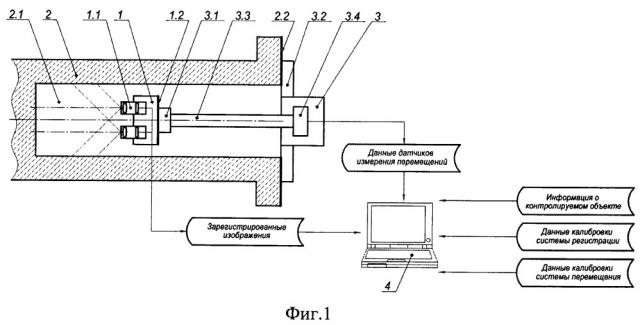
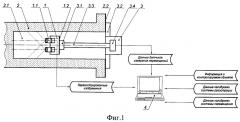
Изобретение поясняется чертежом на Фиг. 1, на котором представлена схема устройства для реализации заявленного способа, где 1 - система регистрации изображений, 2 - контролируемый объект, 3 - система позиционирования, 4 - вычислительный модуль и интерфейс взаимодействия с пользователем.

Система регистрации изображений (поз. 1.1) позволяет одновременно получить несколько изображений объекта с разных ракурсов или одно изображение, отдельные части которого содержат вид объекта с разных ракурсов. Система регистрации может быть реализована в виде:

- нескольких устройств регистрации на основе матричного приемника излучения (МПИ) и отдельных оптических систем ОС;

- одного устройства регистрации на основе нескольких МПИ и одной составной ОС;

- одного устройства регистрации на основе одного МПИ и одной составной ОС.

На Фиг. 1 в качестве примера показана система регистрации изображений, состоящая из двух устройств регистрации 1.1 на основе МПИ и отдельных оптических систем. Расположение нескольких устройств регистрации или отдельных частей составной ОС в пространстве жестко фиксировано перед измерением и не изменяется в процессе проведения измерений. Геометрические характеристики, описывающие эту конфигурацию элементов, заданные в системе координат (СК) системы регистрации, определяются с помощью процедуры калибровки системы регистрации перед началом измерений и хранятся в памяти вычислительного модуля 4. Система регистрации должна иметь базовую поверхность (поз. 1.2), к которой прикрепляется система позиционирования.

Контролируемый объект (поз. 2) имеет полость (поз. 2.1), поверхность которой подвергается визуально-измерительному контролю, и базовую поверхность (поз. 2.2). Предлагаемый метод решает задачу измерения площади участков поверхности контролируемой полости, которая имеет известную сложную форму. К базовой поверхности объекта прикрепляется система позиционирования.

Система позиционирования (поз. 3) осуществляет перемещение системы регистрации относительно контролируемого объекта и определяет положение и ориентацию СК системы регистрации относительно СК контролируемого объекта с известной погрешностью. Система позиционирования содержит:

- узел фиксации (поз. 3.1) базовой поверхности системы регистрации;

- узел фиксации (поз. 3.2) базовой поверхности контролируемого объекта;

- устройство перемещения (поз. 3.3) узла фиксации системы регистрации относительно узла фиксации контролируемого объекта;

- датчики измерения перемещения (поз. 3.4) узла фиксации системы регистрации относительно узла фиксации контролируемого объекта.

Система позиционирования должна обеспечить перемещение системы регистрации в контролируемой полости таким образом, чтобы иметь возможность провести измерение площади поверхностных дефектов на всей поверхности контролируемой полости с требуемой погрешностью. Количество требуемых степеней свободы устройства перемещения и диапазоны перемещения определяются формой контролируемой полости.

Для системы позиционирования должен быть известен метод, позволяющий рассчитать взаимное положение базовой поверхности контролируемого объекта относительно базовой поверхности системы регистрации на основе информации, полученной с датчиков измерения перемещения системы позиционирования. Вычисление положения СК системы регистрации относительно СК контролируемого объекта производится на основе

- информации, полученной с датчиков измерения перемещения системы позиционирования;

- метода расчета взаимного положения базовой поверхности базовой поверхности контролируемого объекта относительно базовой поверхности системы регистрации;

- информации о форме базовой поверхности контролируемого объекта, заданной в СК контролируемого объекта;

- информации о форме базовой поверхности системы регистрации, заданной в СК системы регистрации.

Параметры, необходимые для реализации этого метода, определяются в результате калибровки системы перемещения и хранятся в памяти вычислительного модуля.

В памяти вычислительного модуля также содержится априорная информация о трехмерной структуре контролируемого объекта, заданной в виде трехмерной модели объекта, полученной в результате измерений объекта с использованием соответствующей аппаратуры (3D сканера и др.), или чертежа объекта с указанием номинальных размеров и диапазонов допустимых отклонений. В априорную информацию о контролируемом объекте должна входить информация о форме поверхности контролируемой полости и информация о форме базовой поверхности, заданных в СК контролируемого объекта.

Вычислительный модуль выполняет функции обработки изображений и извлечения из них всей необходимой информации, расчета трехмерных координат точек и площадей участков поверхности, а также оценки погрешности вычисления трехмерных координат точек и площадей. Исходными данными являются зарегистрированные изображения, поступающие от системы регистрации изображений, данные датчиков измерения перемещений, а также данные, хранящиеся в памяти вычислительного модуля: априорная информация о контролируемом объекте, данные калибровки системы регистрации и данные калибровки системы перемещения. Как правило, вычислительный модуль предусматривает интерфейс взаимодействия с пользователем, при помощи которого пользователь задает кривые линии, ограничивающие измеряемый участок поверхности на изображениях, или контролирует результат автоматического выделения таких линий алгоритмом обработки изображений. Результаты расчетов сохраняются в памяти вычислительного модуля и могут быть продемонстрированы пользователю при помощи упомянутого интерфейса.

Устройство работает следующим образом.

До начала работы в память вычислительного блока должны быть загружены априорная информация о контролируемом объекте, данные калибровки системы регистрации и данные калибровки системы перемещения.

Для описания системы регистрации используется математическая модель, описанная в ряде работ [Горевой А.В., Мачихин А.С., Перфилов A.M. Определение погрешности бесконтактного измерения площади дефектов на поверхностях сложной формы при видеоэндоскопическом контроле // Научно-технический вестник информационных технологий, механики и оптики. 2014. №4 (92). С. 140-148; С. 3D computer vision. Efficient methods and applications. 2nd ed. London, UK: Springer Verlag, 2013. 382 p. Chapter 1.1, pp. 3-7; Горевой А.В., Колючкин В.Я. Методы оценки погрешности измерения координат в комплексированных системах регистрации трехмерных образов объектов // Инженерный журнал: наука и инновации. 2013. №9(21). С. 45], которая задается преобразованием , где x_g и p_i - координаты точек объекта в глобальной системе координат (ГСК) и координаты их изображений для i-го устройства регистрации; i-1…M, М - количество устройств регистрации; E_i - оператор преобразования координат из ГСК в СК, связанную с i-м устройством регистрации; P_i - оператор преобразования, определяющего соответствие между трехмерными координатами точек в СК i-го устройства регистрации и двумерными координатами их изображений. В случае использования одного устройства регистрации на основе одного МПИ и составной ОС для получения изображения, отдельные части которого содержат вид объекта с разных ракурсов, координаты точек p_i будут заданы в разных частях этого изображения, а математическая модель «i-го устройства регистрации» будет описывать процесс получения i-й части изображения. Результатом калибровки системы регистрации являются данные калибровки в виде вектора параметров v, описывающего все операторы преобразований P_i и E_i.

Априорная информация о форме контролируемой полости задается в виде преобразования х=W(а), связывающего координаты х точек, принадлежащих поверхности, и вектора параметров положения а. В данном случае координаты х приводятся в СК, связанной с задаваемой поверхностью, для перехода в ГСК нужно использовать преобразование x_g=E_s(x). Определение данного преобразования производится в процессе работы системы на основе данных, поступающих с датчиков системы перемещения, и данных калибровки системы перемещения. Для простоты дальнейшего описания введем вектор параметров v_s, описывающий операторы преобразований E_s и W. Например, для цилиндрической поверхности вектор а может быть задан в виде вектора координат в цилиндрической СК, оператор W будет описывать переход из цилиндрической СК в декартову СК, а вектор параметров v_s будет включать радиус цилиндрической поверхности.

В начале работы система регистрации изображений вводится во внутреннюю полость объекта и перемещается при помощи системы позиционирования. При этом постоянно производится регистрация изображений и их демонстрация пользователю с целью осуществления визуального контроля поверхности внутренней полости. Пользователь осуществляет управление перемещением системы регистрации таким образом, чтобы выполнить осмотр всей подлежащей контролю поверхности и добиться наилучших условий регистрации изображений для каждого участка поверхности. При обнаружении участка поверхности, подлежащего измерению, пользователь при помощи интерфейса дает команду начать измерение.

По команде пользователя зарегистрированные изображения и данные с датчиков перемещения передаются в вычислительный блок для обработки. На данном этапе оператором или автоматически при помощи некоторого алгоритма обработки изображений производится задание границы участка как набора соответствующих точек на изображениях и определяются их координаты: - вектор двумерных координат проекций j-й точки в плоскостях изображений М устройств регистрации, - двумерные координаты проекции j-й точки на изображении, полученном i-м устройством регистрации (или на i-й части одного изображения). Также на данном этапе на основе данных, поступающих с датчиков системы перемещения, априорной информации и данных калибровки системы перемещения производится вычисление вектора параметров v_s.

Далее для каждой точки производится вычисление трехмерных координат x_g по М проекциям p_i при помощи алгоритма триангуляции Т. Данный алгоритм можно представить как поиск оценки вектора , минимизирующей некоторый критерий С [Горевой А.В., Мачихин А.С., Перфилов A.M. Определение погрешности бесконтактного измерения площади дефектов на поверхностях сложной формы при видеоэндоскопическом контроле // Научно-технический вестник информационных технологий, механики и оптики. 2014. №4 (92). С. 140-148; С. 3D computer vision. Efficient methods and applications. 2nd ed. London, UK: Springer Verlag, 2013. 382 p. Chapter 1.1, pp. 3-7]:

При использовании априорной информации о форме поверхности алгоритм триангуляции Т рассматривается как поиск оценки вектора параметров положения [Горевой А.В., Мачихин А.С., Перфилов A.M. Определение погрешности бесконтактного измерения площади дефектов на поверхностях сложной формы при видеоэндоскопическом контроле // Научно-технический вестник информационных технологий, механики и оптики. 2014. №4 (92). С. 140-148]:

Трехмерные координаты точки в ГСК в таком случае можно получить, используя преобразование .

Площадь поверхности объекта вычисляется как сумма площадей криволинейных поверхностей (если поверхность объекта задана аналитически) или треугольников, вершины которых находятся как на заданном контуре, ограничивающем участок поверхности, так и внутри заданного контура (если поверхность объекта задана массивом трехмерных координат точек). Без учета априорной информации о форме поверхности известны и используются только трехмерные координаты точек, находящихся на заданном контуре. При вычислении площади поверхности S_пов определяется как сумма площадей Р треугольников

где S_трi - площадь i-го треугольника, x_i,j - трехмерные координаты j-й вершины i-го треугольника в любой из СК. При вычислении площади поверхности S_пов как сумма площадей Р элементов криволинейной поверхности

где S_элi - площадь i-го элемента криволинейной поверхности.

На следующем этапе производится оценка погрешности измерения площади участка поверхности. Дисперсия погрешности измерения площади i-го треугольника S_i вычисляется как

где - трехмерные координаты j-й вершины треугольника в глобальной системе координат (ГСК), - совместная матрица ковариации погрешности измерения трехмерных координат в ГСК для трех вершин треугольника. Дисперсия погрешности измерения суммы площадей Р треугольников S равна

где - совместная матрица ковариации погрешности измерения трехмерных координат в ГСК для N точек, являющихся вершинами треугольников. Такая матрица в приближении, что трехмерные координаты каждой точки вычисляются независимо, может быть вычислена по формуле

где - матрица ковариации погрешности измерения двумерных проекций j-й точки в плоскостях изображений М устройств регистрации, - матрица ковариации погрешности измерения вектора v, - матрица ковариации погрешности измерения вектора v_s. Матрица определяется погрешностью задания трехмерной структуры объекта и ее положения относительно измерительной системы. При использовании алгоритма вычисления площади, не учитывающего информацию о форме поверхности, для вычисления матрицы используются только два первых слагаемых.

Частные производные для j-й точки вычисляются по следующим формулам:

где

Частные производные вычисляются для каждой точки в соответствии с используемыми операторами преобразований P_i, E_i, E_s и W.

При использовании алгоритма вычисления площади, не учитывающего информацию о форме поверхности, частные производные можно вычислить по схожим формулам

В этом случае частные производные вычисляются для каждой точки в соответствии с используемыми операторами преобразований P_i и E_i.

Полученные оценки дисперсии погрешности вычисления площади для алгоритма, учитывающего априорную информацию о поверхности, и алгоритма, не учитывающего эту информацию, позволяют сделать вывод о преимуществе одного из алгоритмов в данных условиях и использовать результаты, полученные данным алгоритмом. Этим достигается поставленный технический результат.

Триангуляционный метод измерения площади участков поверхности внутренних полостей объектов известной формы, заключающийся в контролируемом перемещении системы регистрации изображений относительно базовой поверхности объекта, записи в цифровом виде нескольких изображений поверхности объекта с различных ракурсов при помощи системы регистрации, сопоставлении синхронно записанных изображений, обнаружении на них искомых участков поверхности и выделении границ этих участков в виде последовательности граничных точек на замкнутой кривой, определении положения пространственного образа граничных точек и вычислении путем триангуляции площади поверхности, натянутой на пространственный образ границы, отличающийся тем, что одновременно с записью изображений осуществляется измерение положения и ориентации системы регистрации относительно базовой поверхности объекта, дополнительно задается множество опорных точек изображения внутри границы, плотность расположения которых определяется требуемой точностью измерений, определяется положение их пространственных образов с учетом их расположения на поверхности, имеющей локальную форму объекта, вычисляется путем триангуляции площадь участка построенной поверхности с использованием как точек на границе, так и дополнительно заданных точек.