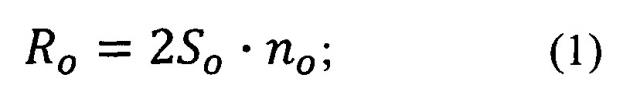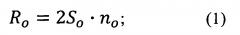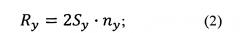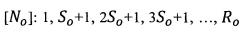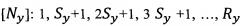Способ получения тканей шашечных переплетений

Способ получения тканей шашечных переплетений

Иллюстрации

Показать все

Реферат

Изобретение относится к производству текстильных материалов и касается изготовления тканей шашечных переплетений, относящихся к классу мелкоузорчатых, вырабатываемых на ткацких станках, оснащенных жаккардовым зевообразовательным механизмом.

Известен способ получения тканей шашечных переплетений, создающий на поверхности ткани рисунок в виде квадратов, напоминающих шахматную доску, в одном квадрате строят лицевую сторону какого-либо переплетения (саржевого, атласного), а в другом квадрате, примыкающем к первому, строят изнанку этого переплетения [Грановский Т.С. Строение и анализ ткани. - М.: Легпромбытиздат, 1985, с. 60-61]. На границах квадратов - клеток - против основных перекрытий располагаются уточные, а против уточных - основные. Всего в раппорте переплетения располагают четыре квадрата. Раппорты базовых переплетений повторяют в квадратах один или несколько раз.

Недостатком описанного способа является невозможность получения на поверхности ткани визуального эффекта полусфер.

За прототип принят способ получения тканей шашечных переплетений, создающий на поверхности ткани рисунок в виде нескольких объемных полос [Пат. 2519921 Российская Федерация, МПК D03D 23/00. Способ получения тканей шашечных переплетений / Толубеева Г.И., Коробов Н.А., Кольцов С.С., Шопыгин А.Е., Яблокова Д.С.; заявитель и патентообладатель ГОУ ВПО «Ивановская государственная текстильная академия». №2012147939/12; заявл. 13.11.2012; опубл. 20.06.2014. Бюл. №17. - 11 с.: 4 ил.]. Визуальный эффект объемных продольных или поперечных полос на ткани получают за счет изменения в раппорте исходного шашечного переплетения ширины отдельных шашек по одной системе нитей: для создания продольных полос - по основе, поперечных - по утку.

Недостатком способа-прототипа является невозможность получения рисунков переплетений с имитацией объемных полусфер, что сужает ассортимент тканей с эффектом объемных геометрических фигур различных конфигураций.

Техническим результатом изобретения является расширение ассортимента тканей комбинированных переплетений путем получения на их поверхности визуального эффекта одной или нескольких объемных выпуклых или вогнутых полусфер.

Указанный технический результат достигается тем, что в способе получения тканей шашечных переплетений, заключающемся в формировании рисунка в виде псевдообъемных фигур второго порядка путем изменения размеров отдельных шашек в раппорте исходного шашечного переплетения, предварительно задаваясь цветом нитей обеих систем, базовым переплетением в шашках, размерами исходных шашек по нитям обеих систем и количеством их пар, рассчитывая раппорты переплетения, формируя модель исходного шашечного переплетения с последующими имитацией деформирования шашечного узора на ткани и получением раппорта деформированного шашечного переплетения, согласно изобретению, в раппорте переплетения формируют участок с одной или несколькими либо выпуклыми, либо вогнутыми, либо выпуклыми с вогнутыми одновременно полусферами, для чего, учитывая цвет нитей обеих систем, задают базовые переплетения в шашках и матрицы их описания, количество, вид и координаты центров с=[x_o, y_o] полусфер, радиус r каждой полусферы, ширину S_o и высоту S_y каждой шашки, количество их пар по ширине n_o и высоте n_y в раппорте переплетения; определяют раппорты переплетения:

находят координаты смены цвета шашек (номера нитей) по основе и по утку:

; ;

получают матрицу цвета точек исходного шашечного поля D(R_y, R_o) с элементами, соответствующими шашкам черного цвета, равными единице, белого цвета, равными нулю; на плоскости раппорта выстраивают модель исходного шашечного рисунка с заданными размерами шашек, окрашивают точки рисунка в черный или белый цвет в соответствии со значениями элементов матрицы D(R_y, R_o); формируют две матрицы переплетений A(R_y, R_o) и B(R_y, R_o); получают матрицу G(R_y, R_o) расстояний от каждой точки рисунка, находящейся в строке x и столбце y, до центра полусферы по выражению

точки, расстояние от которых до центра полусферы меньше ее радиуса, находящиеся внутри полусферы и окрашенные в заданный цвет, переносят в новое положение, оставляя угол относительно центра прежним; рассчитывают элементы матрицы GN(R_y, R_o) новых расстояний от каждой точки рисунка до центра выпуклой полусферы по выражению (4), вогнутой - по выражению (5):

для точек шашечного рисунка, которые изменили свое положение, определяют новые координаты на поле [xn,yn], для остальных точек новые координаты приравнивают старым:

определяют значения элементов матрицы DN(R_y, R_o) нового цвета точек шашечного поля: для каждой пары новых координат [xn,yn] находят ближайшую пару исходных координат [x, y], элементу матрицы DN(x, y) присваивают значение элемента матрицы D(xn, yn); по данным матрицы DN(R_y, R_o) на плоскости раппорта выстраивают модель деформированного шашечного рисунка с имитацией полусферы; в соответствии со значениями элементов матрицы DN(R_y, R_o) формируют матрицу C(R_y, R_o) переплетения: для единичных значений элементов i-й строки j-го столбца матрицы DN(i, j) элементам матрицы C(i, j) присваивают значения элементов матрицы A(i, j), для нулевых - матрицы B(i, j); по данным матрицы C(R_y, R_o) получают переплетение ткани: перекрытия, соответствующие элементам, равным единице, принимают основными, равным нулю - уточными.

Технический результат, заключающийся в расширении ассортимента тканей комбинированных переплетений путем получения на их поверхности визуального эффекта одной или нескольких объемных выпуклых или вогнутых полусфер, достигается за счет искажения вида и размеров отдельных шашек при их неизменном числе в раппорте исходного шашечного переплетения по обеим системам нитей.

Изобретение поясняется чертежами, где

- на фиг. 1 изображены: базовые переплетения для темных (фиг. 1-а) и светлых (фиг. 1-б) шашек, исходное шашечное поле для переплетений примеров (фиг. 1-в);

- на фиг. 2 представлены: модель получаемого шашечного рисунка (фиг. 2-а), раппорт переплетения с визуальным эффектом выпуклой полусферы (фиг. 2-б) и макет ткани (фиг. 2-в);

- на фиг. 3 представлены: модель получаемого шашечного рисунка (фиг. 3-а), раппорт переплетения с визуальным эффектом вогнутой полусферы (фиг. 3-б) и макет ткани (фиг. 3-в);

- на фиг. 4 представлены: модель получаемого шашечного рисунка (фиг. 4-а), раппорт переплетения с визуальным эффектом нескольких полусфер (фиг. 4-б).

Пример практического осуществления способа.

Принимают цвет нитей обеих систем, например, нити основы темного цвета, нити утка - светлого; базовые переплетения в шашках с учетом цвета нитей систем: при нитях основы темного цвета для темных шашек принимают переплетение с основным эффектом, для светлых - переплетение с уточным эффектом, при нитях основы светлого цвета - наоборот, например, для темных шашек атлас 5/3 (фиг. 1-а), для светлых - сатин 5/3 (фиг. 1-б) с раппортами R_об=5 и R_уб=5 нитей. Для каждого базового переплетения получают матрицы a(R_уб, R_об) и b(R_уб, R_об). Элементы матриц, соответствующие основным перекрытиям, принимают, равными 1, уточным перекрытиям - 0:

Принимают вид полусферы, например, выпуклая, координаты центра полусферы [x_o, y_o]=[150, 150], радиус полусферы r=120 нитей, ширину и высоту каждой шашки: S_o=15 нитей, S_y=15 нитей, количество пар шашек по ширине и по высоте в раппорте переплетения: n_o=10, n_y=10. По формулам (1) и (2) определяют раппорты переплетения:

R_o=2S_o⋅n_o=2⋅15⋅10=300 нитей;

R_y=2S_y⋅n_y=2⋅15⋅10=300 нитей.

Находят координаты смены цвета шашек (номера нитей) по основе и по утку:

[N_o]: 1, S_o+1, 2S_o+1, 3S_o+1, …, R_o=1, 16, 31, 46, 61, …, 241, 256, 271, 286, 300; [N_y]: 1, S_y+1, 2S_y+1, 3S_y+1, …, R_y=1, 16, 31, 46, 61, ..., 241, 256, 271, 286, 300. В соответствии с координатами смены цвета шашек [N_o] и [N_y] получают матрицу цвета точек исходного шашечного поля D(R_y, R_o), заполненную элементами, равными 0 или 1. Значение элемента матрицы D(R_y, R_o), равное единице, соответствует окрашиванию точки рисунка в черный цвет, равное нулю - в белый цвет. По данным матрицы D(R_y, R_o) на плоскости раппорта выстраивают модель исходного шашечного рисунка с заданными размерами шашек, окрашивая точки рисунка в черный или белый цвет в соответствии со значениями элементов матрицы D(R_y, R_o) (фиг. 1-в). Формируют две матрицы переплетений A(R_y, R_o) и B(R_y, R_o) путем повторения матриц базовых переплетений a(R_уб, R_об) и b(R_уб, R_об). Получают матрицу G(300, 300) расстояний от каждой точки рисунка, находящейся в строке x и столбце y, до центра полусферы по выражению (3), например, для точки с координатами [x, y]=[1, 1], находящейся в первой строке первого столбца, и координатами центра [x_o, x_y]=[150, 150], получим:

,

для точки с координатами [x, y]=[100, 120], находящейся в сотой строке сто двадцатого столбца, получим:

.

Точки, расстояние от которых до цента полусферы меньше ее радиуса, находящиеся внутри полусферы и окрашенные в заданный цвет, переносят в новое положение, оставляя угол относительно центра прежним. Рассчитывают элементы матрицы GN(300, 300) новых расстояний от каждой точки рисунка до центра выпуклой полусферы по выражению (4). Для примера определим новое расстояние для точки с координатами [x, y]=[100, 120]. Первоначальное расстояние было меньше радиуса сферы, равного r=120, составляло g_100,120=58,3095, по выражению (4) получим:

Для точек, лежащих за пределами радиуса полусферы, расстояние до центра полусферы оставляют прежним, например, для точки с координатами [x, y]=[1, 1] первоначальное расстояние составляло g_1,1=210,7178, больше радиуса полусферы, поэтому новое расстояние принимают равным первоначальному, по выражению (4) получим gn_1,1=g_1,1=210,7178. Для точек шашечного рисунка, которые изменили свое положение, определяют новые координаты на поле [xn, yn] по формуле (6). Рассчитывают новые координаты для точки, например с первоначальными координатами

Новые координаты точек за пределами радиуса полусферы принимают равными старым, например для точки с первоначальными координатами [x, y]=[1, 1] новые координаты составят [xn, yn]=[x, y]=[1, 1]. Определяют значения элементов матрицы DN(300, 300) нового цвета точек шашечного поля: элементам матрицы, которые не изменили своего положения, присваивают значения элементов матрицы цвета исходного шашечного поля D(300, 300), а значения остальных элементов матрицы DN(x, y) принимают равными значениям элементов матрицы цвета исходного поля с новыми координатами D(xn, yn). Для примера значение элемента матрицы DN(100,120) принимаем равным значению элемента матрицы D(118,131) и равным единице. По данным матрицы DN(R_y, R_o) на плоскости раппорта выстраивают модель деформированного шашечного рисунка с имитацией полусферы (фиг. 2-а). В соответствии со значениями элементов матрицы DN(R_y, R_o) формируют матрицу C(R_y, R_o) переплетения: для единичных значений матрицы DN(i,j) элементам матрицы C(i, j) присваивают значения элементов матрицы A(i, j), для нулевых - матрицы B(i, f). По данным матрицы C(R_y, R_o) выстраивают переплетение ткани, учитывая, что строкам матрицы соответствуют нити утка, столбцам - нити основы. Перекрытия, соответствующие элементам, равным единице, принимают основными, нулю - уточными (фиг. 2-б), строят макет ткани (фиг. 2-в).

Ткани с визуальным эффектом вогнутой полусферы (фиг. 3-б), нескольких выпуклых и вогнутых полусфер одновременно (фиг. 4-б) получают аналогично тканям с эффектом выпуклой полусферы (фиг 2-б). Исходные данные для получения переплетений тканей, представленных на фиг. 3-б и 4-б, соответствуют примеру, представленному на фиг 2-б.

В примере с четырьмя полусферами (фиг. 4) количество пар шашек по ширине и по высоте в раппорте переплетения составляет: n_o=20, n_y=20, раппорты переплетения по формулам (1) и (2) составляют R_o=600 нитей, R_y=600 нитей, координаты центров вогнутых полусфер [x_o1, y_o1]=[150, 150], [x_o4, y_o4]=[450, 450], выпуклых полусфер [x_o2, y_o2]=[150, 450], [x_o3,y_o3]=[450, 150].

Число разнопереплетающихся нитей основы переплетения, представленного на фиг. 2-б, равно 242, представленного на фиг. 3-б - 235, на фиг. 4-б - 486. Для выработки ткани представленных примеров требуется жаккардовая машина.

Способ получения тканей шашечных переплетений, заключающийся в формировании рисунка в виде псевдообъемных фигур второго порядка путем изменения размеров отдельных шашек в раппорте исходного шашечного переплетения, предварительно задаваясь цветом нитей обеих систем, базовым переплетением в шашках, размерами исходных шашек по нитям обеих систем и количеством их пар, рассчитывая раппорты переплетения, формируя модель исходного шашечного переплетения с последующими имитацией деформирования шашечного узора на ткани и получением раппорта деформированного шашечного переплетения, отличающийся тем, что в раппорте переплетения формируют участок с одной или несколькими либо выпуклыми, либо вогнутыми, либо выпуклыми с вогнутыми одновременно полусферами, для чего, учитывая цвет нитей обеих систем, задают базовые переплетения в шашках и матрицы их описания, количество, вид и координаты центров с=[x_o, y_o] полусфер, радиус r каждой полусферы, ширину S_o и высоту S_y каждой шашки, количество их пар по ширине n_o и высоте n_y в раппорте переплетения; определяют раппорты переплетения:

находят координаты смены цвета шашек (номера нитей) по основе и по утку: [N_o]: 1, S_o+1, 2S_o+1, 3S_o+1, …, R_o; [N_y]: 1, S_y+1, 2S_y+1, 3S_y+1, …, R_y; получают матрицу цвета точек исходного шашечного поля D(R_y, R_o) с элементами, соответствующими шашкам черного цвета, равными единице, белого цвета, равными нулю; на плоскости раппорта выстраивают модель исходного шашечного рисунка с заданными размерами шашек, окрашивают точки рисунка в черный или белый цвет в соответствии со значениями элементов матрицы D(R_y, R_o); формируют две матрицы переплетений A(R_y, R_o) и B(R_y, R_o); получают матрицу G(R_y, R_o) расстояний от каждой точки рисунка, находящейся в строке x и столбце y, до центра полусферы по выражению

точки, расстояние от которых до центра полусферы меньше ее радиуса, находящиеся внутри полусферы и окрашенные в заданный цвет, переносят в новое положение, оставляя угол относительно центра прежним; рассчитывают элементы матрицы GN(R_y, R_o) новых расстояний от каждой точки рисунка до центра выпуклой полусферы по выражению (4), вогнутой - по выражению (5):

для точек шашечного рисунка, которые изменили свое положение, определяют новые координаты на поле [xn, yn], для остальных точек новые координаты приравнивают старым:

определяют значения элементов матрицы DN(R_y, R_o) нового цвета точек шашечного поля: для каждой пары новых координат [xn, yn] находят ближайшую пару исходных координат [х, у], элементу матрицы DN(x, y) присваивают значение элемента матрицы D(xn, yn); по данным матрицы DN(R_y, R_o) на плоскости раппорта выстраивают модель деформированного шашечного рисунка с имитацией полусферы; в соответствии со значениями элементов матрицы DN(R_y, R_o) формируют матрицу C(R_y, R_o) переплетения: для единичных значений элементов i-й строки j-го столбца матрицы DN(i, j) элементам матрицы C(i, j) присваивают значения элементов матрицы A(i, j), для нулевых - матрицы B(i, j); по данным матрицы C(R_y, R_o) получают переплетение ткани: перекрытия, соответствующие элементам, равным единице, принимают основными, равным нулю - уточными.