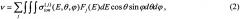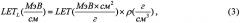Способ оценки стойкости элементов цифровой электроники к эффектам сбоев от воздействия единичных частиц

Способ оценки стойкости элементов цифровой электроники к эффектам сбоев от воздействия единичных частиц

Иллюстрации

Показать все

Реферат

Изобретение относится к способам испытаний полупроводниковых приборов на стойкость к воздействию тяжелых заряженных частиц (ТЗЧ, или ионов) различных энергий космического пространства (КП) по результатам испытаний на стойкость к воздействию ионизирующих излучений (ИИ) моделирующих установок: 1) к импульсному реакторному гамма-нейтронному излучению; 2) импульсному рентгеновскому излучению электрофизических установок (генераторов рентгеновского излучения, линейных ускорителей, циклотронов); 3) ускорителей заряженных частиц; 4) импульсного лазерного излучения, с использованием коэффициентов относительной эффективности (КОЭ) заданных уровней ИИ к излучениям моделирующих установок (МУ).

Особое место при исследовании стойкости больших интегральных схем (БИС) технологии «комплементарные структуры «металл-диэлектрик-полупроводник» - на - диэлектрике» (КМОП/КНД, далее МДП) занимают эффекты отказов от единичных сбоев SEE (Single event effect) /1-3/.

Эффекты SEE подразделяются на «мягкие» и «жесткие» ошибки. Остаточные «жесткие» ошибки проявляются комплексно.

Источниками SEE в чувствительных объемах БИС являются протоны высоких энергий, электроны и ТЗЧ, которые с определенной вероятностью могут вызвать ядерные реакции с последующей ионизацией материала осколками деления, и ТЗЧ, которые вызывают «воронки заряда» вдоль трека распространения, что создает, в свою очередь, или переходный процесс или постоянные деструктивные эффекты.

Известен способ определения стойкости полупроводниковых приборов к электронному или протонному излучениям КП, заключающийся в облучении приборов электронным или протонным пучком на линейном ускорителе или циклотроне и измерении параметров до и после облучения /4/.

Недостатком указанного способа является высокая стоимость подобных испытаний и малая доступность установок, создающих протоны (электроны) определенного энергетического диапазона.

Испытания элементной компонентной базы (ЭКБ) на ускорителях, формирующих ТЗЧ, в соответствии с процедурой, представленной на Фиг. 1, позволяют установить абсолютное значение поперечного сечения в [см²] для SEE, которое является характеристикой чувствительности (стойкости) испытываемой БИС при облучении моноэнергетическим и мононаправленным пучком частиц j-го сорта (Фиг. 2):

где ν - количество (или частота, с^-1) SEE, возникающих в БИС при облучении; N_(j)=Ф×cosθ - количество (или интенсивность) частиц данного типа из их общего потока F_I (или общей плотности потока, см^-2⋅с^-1), см^-2, который падает под углом θ на поверхность элемента ЭКБ, имеющего площадь S (Фиг. 3). Энергетические характеристики частиц ускорителей наиболее близки к характеристикам ТЗЧ КП и, как правило, имеют высокую проникающую способность. Такие испытания позволяют установить наиболее точные абсолютные значения сечения для SEE при воздействии частиц j-го сорта в зависимости от их энергии и углов падения (полярного θ и азимутального ϕ) и могут быть непосредственно использованы для прогнозирования количества или частоты SEE ν при воздействии изотропных ((θ, ϕ=const) потоков ТЗЧ разного сорта и энергии по формуле:

где F_j(E) - дифференциальный энергетический спектр направленного потока, в единицах [см^-2⋅стеррад^-1(МэВ/нуклон)^-1], или плотности потока в единицах [см^-2⋅ср^-1(МэВ/нуклон)^-1⋅с^-1], частиц j-го сорта. Здесь «ср» - означает стеррадиан (единица телесного угла).

Определение значений на ускорителях частиц в зависимости от нескольких параметров (сорта частиц, их энергии и углов падения) требует значительных временных и материальных затрат и поэтому существуют затруднения в непосредственном применении на практике для оценки радиационной стойкости (PC) элементов ЭКБ, предназначенных для бортовой радиоэлектронной аппаратуры (РЭА) космического аппарата (КА). Для оптимизации процесса испытаний и сокращения их объема до «разумных» пределов могут быть использованы моделирующие установки (МУ), в том числе исследовательский ядерный реактор (ИЯР) и электрофизические установки (ЭФУ), генерирующие импульсное рентгеновское излучение (РИ).

С целью удешевления испытаний эквивалентную поглощенную дозу гамма-рентгеновского излучения ИЯР или рентгеновского излучения ЭФУ со спектром RS определяют с использованием метода, изложенного в /8/.

Существующие тенденции разработки и изготовления БИС (т.е. сокращение размеров приборов, потребляемой мощности, увеличение линейного разрешения, увеличение объема памяти и быстродействия) могут только увеличить чувствительность к эффектам SEE. Это легко можно увидеть, если представить прибор простым конденсатором (C), в который проникает ионизирующая частица, создающая нестационарный заряд Q_t, в результате чего изменяется напряжение в нагрузке (т.е. логическое состояние). Эффект SEE наблюдается, если линейные потери энергии частиц LET>Q_crit - величины «критического заряда». При уменьшении активной области такого прибора, ее емкость также уменьшается и тот же самый заряд способствует появлению эффектов SEE. Прибор по толщине в основном остается неизмененным, подвергаются изменениям только длина и ширина прибора. Если будем рассматривать транзисторную структуру МДП в виде чипа квадратной конфигурации LxL, то критический заряд Q_C, достаточный для изменения логического состояния такого прибора, будет пропорционален квадрату размера L. Модель «критического заряда» Q_C /7/ пригодна для анализа SEE для интегральных микросхем (ИМС) ряда технологий (включая NMOS, CMOS/объемный, CMOS/SOS, i²L, GaAs, ECL, CMOS/SOI, биполярный VHSIC). Этот критический заряд приводит непосредственно к переключению из состояния логической «1» в состояние логического «0» или изменению логического состояния (конверсии), но он может быть меньше, чем полный радиационно-индуцированный заряд Q_t, из-за длины трека ТЗЧ в чувствительном объеме структуры МДП, который используется в модели «хорды» s (Фиг. 3). Хорда минимальна при нормальном падении ТЗЧ на лицевую или инверсную поверхность чипа структуры МДП и принимает максимальное значение s_max, когда является пространственной диагональю чипа в виде параллелепипеда (Фиг. 3). Существенно то, что Q_C является разницей между зарядом Q_t в узле и минимальным зарядом, необходимым для усиления и последующей конверсии. Для линейных потерь энергии частиц (Linear Energy Transfer) LET_L можно записать:

где LET - массовые потери энергии ТЗЧ; ρ - плотность материала M, тогда полные потери энергии на длине хорды выделенного чувствительного объема структуры МДП составят

Здесь длина максимальной хорды S_MAX транзисторной структуры дается в [см]. Для более корректной оценки генерации зарядов необходимо располагать данными о следующих константах: - постоянной генерации носителей заряда, [Кл см^-3⋅рад^-1(M)]; - предельному значению доли нерекомбинированного радиационно-индуцированного заряда; - фактору дозового накопления гамма-рентгеновского излучения моделирующей установки со спектром квантов RS, а - такие же константы для ионов КП. В большинстве измерений эти величины не могут быть селектированы без принятия определенных допущений /5/.

В табл. 1 приведены пределы изменения величины LET, при которых требуется анализ тех или иных видов излучений КП. Как следует из таблицы, при LET>100 МэВ⋅см²/мг схема считается стойкой и анализа не требуется.

Одна из классических интерпретаций состоит в том, что общая острота кривых поперечного сечения зависит от вариации межячеечной чувствительности к эффектам SEE /9/. Такая интерпретация несомненно более подходит для нерегулярных схем, таких, например, как логические схемы. Однако в случае БИС памяти, такой как статическое запоминающее устройство SRAM (Static Random Access Memory) или динамическое запоминающее устройство DRAM (Dynamic Random Access Memory), тщательное рассмотрение экспериментальных данных включает в большей степени роль внутреннего содержания ячеек, нежели межячеечных различий.

Наиболее близким по технической сущности и принятым за прототип является экспериментально разработанный способ прогнозирования интенсивности сбоев БИС в полях ИИ КП, предложенный в /6/.

В прототипе в качестве альтернативной гипотезы, объясняющей наличие значительной кривизны в области примыкающей к критическому «пороговому» значению LET_TH, в том числе вариации чувствительности БИС к эффектам SEE в пределах одной ячейки, было описано как зависящее от позиционирования («posicion-dependence»), внутренне усиление эффекта SEE. Однако так как эти термины используют разработчики схем для других целей, и поскольку терминология «эффективность собранного заряда» («sharge-collection efficiency») имеет специфическую историю и механистическую импликацию, был введен термин «эффективность» («efficient»). Намерением здесь являлось использование термина, который свойственен всем технологиям, независимо от того, является ли «усиление» (в контексте «gain») большим или меньшим единицы.

В /6/ ввели концепцию эффективности при проверке чувствительности БИС к эффектам SEE, которую можно определить из кривой поперечного сечения. Это приводит к зависимости эффективности вероятности и демонстрирует, каким образом распределение вероятности можно представить графически как функцию фракции чувствительной области. Кривая эффективности может быть также определена путем воздействия импульсного лазера или воздействием ионного микропучка, или путем компьютерной симуляции. Эти кривые позволяют с другой стороны получить информацию о расчете чувствительности к эффектам SEE в качестве критерия добротности («figure of merit» FOM - Добротность есть величина, используемая для характеристики производительности устройства, системы или метода, по отношению к его альтернативе). В результате был проверен диапазон применимости этого метода и получено заключение, что он может быть использован в пределах более чем восьми порядков величины амплитуды индуцированных КП сбоев для геосинхронной орбиты.

В соответствии с ним была принята концепция «эффективности заряда» как мера эффективности индуцированного заряда для создания эффектов сбоя от единичной частицы. Эффективность измерена для чувствительности к эффектам SEE в пределах одной ячейки. Эффективность - это корреляция между местом положения входа частицы (single even (SE) stricke location) и актуальной чувствительностью к сбоям - т.е. отношение физической геометрии прибора к реакции схемы.

Она иллюстрирует, каким образом может быть определена зависимость эффективности из стандартных данных поперечного сечения эффектов SEE для тяжелых ионов или импульсного лазера, и показано, каким образом она может быть рассчитана из комбинации данных о собранном заряде и анализе схемы. Принимают допущение о величине критического заряда Q_C, необходимого для генерации эффекта SEE. Критический заряд, соответствующий энерговыделению LET, соответствует величине 50% поперечного сечения насыщения σ_SAT и ограничен номинальной толщиной прибора /9/ (используют коэффициент преобразования ). График зависимости поперечного сечения в области насыщения σ_SAT аппроксимируют для данных с использованием логарифмически нормального закона или закона распределения Вейбулла. Принимают, что эффективность SEE максимальна, если значение поперечного сечения составляет 50% от предельного значения L_0,5=LET(σ=0,5σ_SAT). Значение максимальной эффективности SEE определяют, как и, естественно, она изменяется как 1/LET. На Фиг. 4. показана аппроксимация логарифмически-нормальным законом зависимости эффективности SEE при моделировании лазерным импульсом от относительной величины площади сбора заряда /6/. На Фиг. 5. приведена типичная кривая аппроксимации зависимости законом распределения Вейбулла (заметные расхождения с экспериментальными данными в области больших значений LET /6/.

Кривые поперечного сечения и эффективности могут быть лучше аппроксимированы с использованием сглаживающего логарифмически-нормального распределения (L-n) вследствие того, что логарифмически-нормальное распределение (Фиг. 4) по сравнению с вейбулловским более соответствует физике прибора /10/.

Отметим, что лог-нормальное распределение (L-n) имеет меньшее количество параметров, чем распределение Вейбулла. Если использовать аппроксимацию кривой поперечных сечений, то лог-нормальное распределение менее выгодно в области малых значений LET. Такое поведение приборов характерно для режима отсечки при высокой эффективности. Расчетные значения интенсивности сбоев на 1-2% больше или меньше при использовании распределения Вейбулла для описания кривой поперечных сечений вместо лог-нормального распределения.

Интенсивность сбоев может быть определена с использованием цифрового представления о характеристиках «добротности» (FOM) и значений, определенных из данных по поперечным сечениям или из симуляции в смешанном режиме.

Кривую эффективности также используют для прогнозирования интенсивности сбоев с включением статистик достоверности эффективности. Скорейшим путем является предварительный расчет значения LET_0,25, при котором поперечное сечение равно 25% от предельного значения поперечного сечения σ_0,25=0,25σ_SAT, и объединение его напрямую с предельным значением поперечно сечения при расчете FOM.

На Фиг. 6. показана зависимость интенсивности сбоев (SEE) от добротности (FOM) /11/. На Фиг. 7. представлены зависимости поперечного сечения SEE, распределения эффективности и аппроксимирующей функции интегрального логарифмически-нормального закона распределения от LET для ИМС IDT 71 256 (R-MOS) /6/.

В более сложных методах кривую поперечного сечения аппроксимируют, и из этой аппроксимации определяют параметры FOM. Медианное значение σ_0,5=0,5σ_SAT или L_0,5 (или «средний» параметр "m") экстрагируется из анализа схемы, классического критического заряда Q_C наряду с предполагаемым процессом эффективности накопленного заряда. Из анализа аппроксимации кривой L-n распределения эффективности (как показано на Фиг. 7) может быть экстрагировано стандартное отклонение (параметр "s").

По этим двум параметрам конструируют FOM:

где σ_HI - предельное значение поперечного сечения на один бит; L_0,25 - значение LET, при котором σ на уровне 25% предельного значения поперечного сечения /11/-/14/. Для L-n распределения L_0,25=m-0,674s.

Известно несколько критических обзоров, посвященных применению FOM /15/-/18/. С использованием предельного поперечного сечения и L_0,25 разработчик может рассчитать интенсивность сбоев для стандартной орбиты, геосинхронной или минимума солнечной активности, как это показано на Фиг. 5. Этот рисунок заимствован из /11/, в которой было отмечено, что точки, относящиеся к ложным, лежат правее прямоугольного участка графика. В диапазоне, простирающимся в область более низких значений LET, очевидно получается аппроксимация квадратичной функцией.

Интенсивность сбоев, проинтегрированная по модели IRPP (Integrated Rectangular Parallel-Piped), имеет основную форму (форма Bredford) /19/

где R - интенсивность сбоев в ячейке, s_MIN=Е_с/ρ⋅LET [см] - минимальная длина хорды (пространственной диагонали) в чувствительном объеме транзисторной структуры, Е_с=22,5Q_c [МэВ] - критическое значение энергии генерации SEE, [Q_c]=nКл - размерность критического заряда, [Е_с]=МэВ - размерность критической энергии, S - площадь поверхности [см²], L₀ - минимальное значение достаточное для генерации сбоев, Ф(L) - дифференциальный спектр L_MAX - максимальное значение LET в спектре Ф(L), C - интегральное распределение длины пути, ρ - плотность материала Сбои можно наблюдать, когда длина хорды ассоциируется с LET (или L) большим чем s_MIN.

При этом принимают, что прибор имеет уникальный критический заряд, Q_C, больше которого наблюдается сбой, и постоянную толщину, а, такую, что Q_C соответствует уникальному значению эффективного значения LET. График основного поперечного сечения в зависимости от эффективного значения LET вводится ступенчатой функцией. Можно переобозначить равенство (6) в виде понятия L_C, т.е. критического значения LET,

где и L₀=L_Ca/s_MAX.

Величину L_C определяют минимальным значением L, при котором частица может вызвать сбой при нормальном падении через ячейку, т.е. пути длиной а. Налетающий поток может генерировать сбои при заданном значении L, если длина пути больше чем L_C/L в величинах а. При больших значениях L путь укорачивается. Минимальное значение L, при котором генерируются сбои, соответствует максимально возможной длине пути (s_MAX). Это значение получается при L=L₀. Для случаев вблизи минимального значения L, которые могут вызвать сбои, соответствующие длины пути очень длинные, соответственно больше чем L_Ca/L.

Экспериментально кривая поперечных сечений никогда не демонстрирует вид ступенчатой функции, которая ассоциируется с простыми трактовками, приведенными выше; она постоянно демонстрирует постепенное плавное увеличение выше так называемого «порогового значения» LET_TH. В /6/ приведены доводы, что диапазон чувствительности к сбоям демонстрирует различные механизмы усиления собранного заряда. В работе /20/, например, содержатся выражения для чувствительности, в виде зависимости от толщины, которая здесь выступает в качестве альтернативы.

Несмотря на то что требуется рассматривать прибор, как имеющий различные области с различной эффективностью, необходимо рассматривать полную ячейку, если рассчитывать накопление энергии, которая проистекает из полного пути частицы в ячейках. Поэтому накопленный заряд в КП в большой степени определяется распределением пути в IRPP.

Поэтому далее в /6/ рассматривают энергию, которая должна быть накоплена на таком особенном пути на кривой зависимости поперечного сечения от LET для инициирования сбоев. Часть кривой с низкими значениями поперечного сечения подразумевает запасенную энергию меньше чем вследствие процесса усиления (gain). LET в этом случае соответствует точке на кривой поперечного сечения, и ее выделяют, помечая из окружающих значений LET те, которые учитываются в расчете интенсивности сбоев. Окружающие точки называют L_e, а лабораторное эффективное значение L. Запасенная энергия, вызывающая сбой, в этом случае будет равна При малых L значение E_dep меньше чем вследствие экстремального значения усиления, которое было, L_Q, минимальное значение L_e, при котором можно наблюдать сбои, может также изменяться. При низких значениях L величина E_dep может быть меньше вследствие механизма усиления. В /6/ введена функция g(L) для определения функции усиления в зависимости от L для выражения зависимости усиления от L. Она является функционалом, из которого проистекает функция поперечного сечения. Отсюда проистекают условия применения полной функции Вейбулла или L-n функции.

Если используют L-n функцию для описания данных, приведенных для малых значений L вблизи отсечки, то применяют эту функцию совместно с нижним пределом L в интегральном распределении L. Это может привести к 1-2% улучшению результатов расчетов, однако, очень не на много улучшается прогноз интенсивности сбоев /21/:

где L₀=La/s_MAX; s_MIN=L/L_ea; g(L) - распределение Вейбулла или L-n, dS(L) - дифференциальный элемент площади, соответствующий g(L). Интегрирование по dS(L) является независимым от других членов, что приводит к соотношению

Соответствующее уравнение может быть получено с использованием интегрального распределения и дифференциального распределения длин хорд /9/.

Этот результат является идентичным тому, который получается при принебрежении вариаций внутри ячейки при оценке чувствительности к SEE /9/.

В результате выполненной в /6/ перепроверке стандартного метода представления чувствительного объема в виде IRPP для расчета интенсивности SEE в допущении, что вероятность сбоев зависит от положения бита на поверхности, было сделано заключение, что является нецелесообразным переформулировка IRPP.

В /6/ экспериментальная зависимость начинается при LET=0 из начала координат (0,0) (Фиг. 7). Поэтому аппроксимация зависимости теоретическим L-n законом распределения учитывает этот факт, а экстрагированные параметры распределения включают эту информацию.

Сборка UTMC "Summit" была тестирована 17.05.2000 на чувствительность к отказам от SEE и интенсивность отказов на циклотроне "88-inch Cyclotron" Lawrence Berkeley Laboratory.

Однако представленные на Фиг. 8 результаты тестирования БИС вентильных матриц "JS01 Summit", изготовленных по технологии UTMC 0,6 μm Commercial RadHard™ (CRH), дают минимальное значение поперечного сечения σ_MIN=10^-7 см²/бит, а параметры аппроксимирующего интегрального закона распределения Вейбулла дают параметр положения ниже которого интегральная функция

не определена (характеристики зависимости приведены в табл. 2). На том же циклотроне проводились квалификационные испытания на чувствительность к SEE ИМС параллельно-последовательного преобразователя (serializer) UTMC WD11C 3.3V LVDS на воздействие ТЗЧ, или ионов. Данные по чувствительности к эффектам SEE были собраны 14.04.2003 и показаны на Фиг. 9.

Минимальное значение поперечного сечения на графике также составляет σ_MIN=10^-7 см²/бит, в то время как параметр (табл. 2). В тех же условиях 10.07.2003 были проведены исследования чувствительности ИМС 4 Мбит SRAM фирмы "Aeroflex PIC" (WC02 и WC03) к эффектам SEE на 88-дюймовом циклотроне LBNL (Фиг. 10). Аналогично σ_MIN=10^-14 см²/бит, а (табл. 2). Альтернативой модели эффективности является представление о дополнительном локальном формировании накопленного заряда за счет воздействия таких факторов, как атмосферные нейтроны, «эффект упаковки» и естественная фоновая радиоактивность, действующие помимо ионизирующего излучения космического пространства, в том числе на поверхности Земли и на активном участке вывода космического аппарата на орбиту. В области малых значений относительного изменения σ/σ_SAT справедливо аппроксимировать функцию F(LET) экспоненциальным распределением. Если границей нечувствительности к SEE считать значение (табл. 1), то при приращение интенсивности отказа за счет учета дополнительного заряда дает изменение суммарной интенсивности сбоев ΔZ_Σ(LET)=1,3%, что приводит к изменению функции распределения SEE ΔF(LET)=0,4%. Анализ взаимодействия единичных частиц с ЧО с привлечением микродозиметрического подхода дает обоснование как линейному участку на зависимости интенсивности сбоев от флюенса частиц (т.е. величины обратной σ), так и наличию при определенных условиях выхода на участок насыщения σ_SAT. При этом разумным представляется принять распределение таких SEE на участке 0<LET<LET_TH в виде равномерного закона распределения.

На Фиг. 11 показана зависимость интенсивности SEE Z(LET) при аппроксимации функции σ(LET) трехпраметрическим законом распределения Вейбулла при γ=LET_TH, двухпарметрическим законом распределения Вейбулла при γ=0, экспоненциальным законом распределения при Z(LET)=λ на участке 0<LET<LET_TH и равномерным законом распределения (F_U(LET)) с на том же участке. На Фиг. 12 показана зависимость изменения поперечного сечения SEE [см²] от при аппроксимации единичной функции распределения (F₁(LET), трехпраметрическим законом распределения Вейбулла при γ=LET_TH, двухпарметрическим законом распределения Вейбулла при γ=0, двухпараметрическим законом распределения Вейбулла (F_W(η,β)) γ=0 по модели эффективности /6/, при комбинированном законе распределения (Вейбулла + равномерным законом распределения на участке 0<LET<LET_MAX.

В методе /6/, принятом за прототип, не учитывается «предыстория» поведения ИМС до попадания в область LET_TH, например нахождение ИМС на поверхности Земли или на активном участке траектории вывода КА. Кроме этого, имеется проблема «умолчания» поведения кривой в области малых значений LET и наличие ненулевого значения параметра положения.

Техническим результатом предлагаемого способа оценки стойкости элементов цифровой техники к эффектам сбоев от воздействия единичных частиц является повышение точности определения характеристик зависимости поперечного сечения эффектов единичных сбоев (SEE) от LET, а также определение минимального значения флюенса частиц F_MIN, достаточного для генерации эффектов SEE.

Технический результат достигается тем, что в способе оценки стойкости элементов цифровой электроники к эффектам сбоев от воздействия единичных частиц космического пространства путем определения минимального значения потока частиц, соответствующего отличному от нулевого значения сечению сбоев в области малых значений линейной передачи энергии частицами, для чего получают экспериментальную зависимость величины сечения сбоев от величины линейных потерь энергии частиц, аппроксимируют эту зависимость теоретическим многопараметрическим законом распределения, экстрагируют параметры этого распределения, определяют пороговое значение линейных потерь энергии единичных частиц, соответствующего минимальному значению сечения сбоя, определяют максимальное значение сечения сбоев в режиме насыщения и минимальное значение потока частиц, а затем реализуют сопоставление минимальных значений потоков частиц, полученных с использованием следующих математических моделей:

1) в качестве теоретического многопараметрического интегрального закона распределения сечения сбоя для значений, больших величины порогового значения линейных потерь принимают трехпараметрический закон распределения Вейбулла, а для значений, меньших величины порогового значения линейных потерь, но больших величины их нулевого значения, принимают равномерный закон распределения, учитывающий «предысторию» возможности появления единичных сбоев, полагают в качестве критерия равными интенсивности сбоев и определяют сечения сбоев и минимальное значение потока частиц;

2) для вейбулловского и равномерного законов распределения принимают в качестве критерия равными между собой интегральные функции распределения и определяют сечения сбоев и минимальное значение потока частиц;

3) для порогового значения линейных потерь энергии частиц принимают в качестве критерия комбинированную величину интенсивности сбоев, которую определяют в виде суммы величин интенсивности сбоев для равномерного и вейбулловского законов распределения, определяют сечения сбоев и минимальное значение потока частиц;

4) для вейбулловского и равномерного законов распределения определяют величины ресурсов, а в качестве скорректированной величины ресурса для порогового значения линейных потерь энергии частиц принимают в качестве критерия произведение указанных ресурсов, определяют сечения сбоев и минимальное значение потока частиц;

5) принимают в качестве критерия равными интегральные функции распределения сбоев для вейбулловского и равномерного законов распределения, а затем определяют скорректированную пороговую величину линейных потерь энергии частиц, определяемую в виде линейного соотношения соответствующих величин для указанных законов, определяют сечения сбоев и минимальное значение потока частиц;

6) определяют в качестве критерия скорректированный ресурс как произведение ресурсов для вейбулловского и равномерного законов распределения, затем определяют параметры скорректированного закона распределения и получают скорректированное значение минимального потока частиц, определяют сечения сбоев и минимальное значение потока частиц;

7) в качестве критерия равными принимают ресурсы, определенные для вейбулловского и равномерного законов распределения, определяют параметры скорректированного закона распределения, определяют сечения сбоев и минимальное значение потока частиц;

из полученного набора данных выбирают минимальное значение потока частиц (наихудший случай).

Изобретение иллюстрируется следующими чертежами.

Фиг. 1. Схема процедуры оценки зависимости вероятности сбоев от эффектов SEE от флюенса ТЗЧ /22/.

Фиг. 2. Типичная зависимость поперечного сечения SEE σ [см²] от линейных потерь энергии в Si от ионов Fe /8/.

Фиг. 3. Исходная структура чувствительного объема транзистора МОП для расчета LET.

Фиг. 4. Аппроксимация логарифмически-нормальным законом зависимости эффективности SEE при моделировании лазерным импульсом от относительной величины площади сбора заряда /6/.

Efficacy - эффективность

Cumulative relative area - относительная площадь сбора заряда

Фиг. 5. Типичная кривая аппроксимации зависимости законом распределения Вейбулла (заметные расхождения с экспериментальными данными в области больших значений LET /6/.

Фиг. 6. Зависимость интенсивности сбоев (R) от добротности (FOM) /11/

Rate - интенсивность

Calc - расчетные данные

Upset rate - интенсивность сбоев

Figure of merit - добротность

Фиг. 7. Зависимости поперечного сечения SEE, распределения эффективности и аппроксимирующей функции интегрального логарифмически-нормального закона распределения от LET для ИМС IDT 71 256 (R-MOS) /6/.

Фиг 8. Экспериментальные данные и аппроксимация L-n распределением результатов тестирования сборки UTMC "Summit" 17.05.2000 на чувствительность к отказам от SEE и интенсивность отказов на циклотроне "88-inch Cyclotron" Lawrence Berkeley National Laboratory (LBNL).

Cross Section/Device, cm²/bit - поперечное сечение/прибор, см²/бит

Log norm - аппроксимация L-n распределением

Comulative - интегральное L-n распределение

Efficacy - эффективность

Фиг. 9. Результаты испытания 14.04.2003 на чувствительность к SEE ИМС параллельно-последовательного преобразователя (serializer) UTMC WD11C 3.3V LVDS на воздействие ТЗЧ на циклотроне "88-inch Cyclotron" LBNL.

SEU (SEE) Cross Section, cm²/bit - поперечное сечение, см²/бит

Weibull fit - аппроксимайия законом Вейбулла

S/N… - серийный номер

Фиг. 10. Результаты исследования чувствительности 10.07.2003 ИМС 4 Мбит SRAM фирмы "Aeroflex PIC" (WC02 и WC03) к эффектам SEE на циклотроне "88-inch Cyclotron" LBNL.

Cross Section, cm²/bit - поперечное сечение, см²/бит

Weibull fit - аппроксимайия законом Вейбулла

Part… - номер образца

Фиг. 11. Зависимость интенсивности SEE Z(LET) при аппроксимации функции σ(LET) трехпраметрическим законом распределения Вейбулла при γ=LET_TH, двухпарметрическим законом распределения Вейбулла при γ=0, экспоненциальным законом распределения при Z(LET)=λ на участке 0<LET<LET_TH и равномерным законом распределения (F_U(LET)) с на том же участке.

Фиг. 12. Зависимость изменения поперечного сечения SEE [см²] от при аппроксимации единичной функции распределения (F₁(LET), трехпраметрическим законом распределения Вейбулла при γ=LET_TH, двухпарметрическим законом распределения Вейбулла при γ=0, двухпараметрическим законом распределения Вейбулла (F_W(η, β)) γ=0 по модели эффективности /6/, при комбинированном законе распределения (Вейбулла + равномерным законом распределения на участке 0<LET<LET_MAX.

Предлагаемый способ реализуется следующим образом.

На моделирующей установке (МУ) или имитационными методами (ИМ) экспериментально снимают зависимость поперечного сечения σ эффектов SEE от величины LET. В качестве моделирующих установок используют импульсные источники, такие, например, как импульсные ядерные реакторы, электрофизические установки, генерирующие импульсное X-Ray, циклотроны протонного излучения и т.п. /22/, /23/. ИМ реализуют с помощью импульсного лазерного излучения /24/ или методами компьютерного моделирования /25/. Полученную зависимость далее аппроксимируют теоретическим интегральным многопараметрическим законом распределения, экстрагируют параметры этого распределения, определяют пороговое значение LET_TH, соответствующее минимальному значению поперечного сечения SEE σ_MIN, определяют максимальное значения поперечного сечения в режиме насыщения σ_SAT. Затем определяют значения потока частиц F_MIN, соответствующего отличному от нулевому значению поперечному сечению σ_MIN. В качестве теоретического многопараметрического интегрального закона распределения поперечного сечения SEE для значений LET, больших величины порогового значения LET_TH принимают трехпараметрический закон распределения Вейбулла

где LET_TH=γ - параметр положения, η - параметр масштаба, β - параметр формы, а для значений LET, меньших величины порогового значения LET_TH, но больших величины их нулевого значения, принимают интегральный закон распределения, учитывающий «предысторию» возможности появления единичных сбоев SEE.

Для диапазона 0<LET<LET_MAX в качестве плотности исходного распределения поперечного сечения принимают равномерное распределение

с верхним граничным значением равным максимальному значению величины линейной передачи энергии,