Способ определения оптимальной периодичности контроля состояния технических средств и систем при минимальном времени получения результата

Способ определения оптимальной периодичности контроля состояния технических средств и систем при минимальном времени получения результата

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительной технике, в частности к способам контроля, и может быть использовано в практике эксплуатации, где требуется определять оптимальную периодичность контроля при минимальных вычислениях аппроксимирующей функции.

Из существующего уровня техники известны различные определения оптимальной периодичности контроля состояния технических средств и систем.

Известны устройства [Воробьев Г.Н., Гришин В.Д., Марков Д.И. А.С. СССР №1437888, М.: Кл. 4 G07C 3/02, 1988; Воробьев Г.Н., Гришин В.Д, Тимофеев А.Н. А.С. СССР №1679512, М.: Кл. 5 G07C 3/02, 1991], обеспечивающие определение оптимального периода обслуживания сложной системы, реализуя минимаксный критерий. При этом все подсистемы, входящие в сложную систему, должны обслуживаться с одинаковой периодичностью, соответствующей оптимальному периоду самой ненадежной подсистемы. Эти устройства целесообразно использовать для систем, подсистемы которых близки по надежности. Если же подсистемы существенно различаются по надежности, то обслуживание их с одинаковой периодичностью, вычисленной устройствами [Воробьев Г.Н., Гришин В.Д., Марков Д.И. А.С. СССР №1437888, М.: Кл. 4 G07C 3/02, 1988; Воробьев Г.Н., Гришин В.Д., Тимофеев А.Н. А.С. СССР №1679512, М.: Кл. 5 G07C 3/02, 1991] не позволит рационально использовать надежностный потенциал остальных, более надежных систем. Таким образом, можно заключить, что устройства [Воробьев Г.Н., Гришин В.Д., Марков Д.И. А.С. СССР №1437888, М.: Кл. 4 G07C 3/02, 1988; Воробьев Г.Н., Гришин В.Д., Тимофеев А.Н. А.С. СССР №1679512, М.: Кл. 5 G07C 3/02, 1991] обладают ограниченной областью применения. При определении периода обслуживания сложной системы, отсутствует выбор оптимального аргумента аппроксимирующей функции.

Известен способ определения периодичности контроля оперативного запоминающего устройства при функционировании в радиационных условиях космического пространства на солнечно-синхронной орбите [Патент РФ №2438163 С1, класс G06F 11/00, опубл. 27.12.2011 г.].

Способ заключается в оценке условий функционирования оперативного запоминающего устройства, определении интенсивности отказов, определении периодичности контроля.

Недостатком данного способа является ограниченная область применения. Кроме того, результаты контроля указывают только на критические значения параметров. Отсутствуют условия выбора сложности вычислений аппроксимирующей функции, что влияет на время обработки аппроксимирующей функции.

Наиболее близким к предложенному способу является «Способ определения оптимальной периодичности контроля состояния процессов», по патенту РФ №2623791, класс G05B 23/00, G06Q 10/04, заявленный 25.01.16. Способ-прототип заключается в том, что предварительно задают в качестве элементов исходных данных множество аппроксимирующих функций, удовлетворяющих заданным требованиям, задают точность аппроксимации, пределы и шаг изменения параметров аппроксимирующих функций; определяют интенсивность отказов, оценивают условия функционирования объекта контроля, при оценке условий функционирования формируют множество данных о времени и характере воздействия различных дестабилизирующих факторов, фиксируют значения параметров дестабилизирующих факторов, разделяют их на однородные группы, аппроксимируют значения параметров дестабилизирующих факторов каждой из однородных групп аппроксимирующими функциями с заданной точностью, определяют частоту каждой полученной функции, строят вариационный ряд значений частот всех полученных функций, определяют наибольшее значение частоты, определяют оптимальный период контроля согласно выражению T_контр=1/(2ƒ_в), где ƒ_в - наибольшее значение частоты полученных аппроксимирующих функций.

Недостатком способа-прототипа является отсутствие условия выбора аппроксимирующей функции, что влияет на сложность ее вычисления при вычисленной точности аппроксимации и увеличивается время определения оптимальной периодичности контроля.

Технический результат предлагаемого способа заключается в сокращении времени определения оптимальной периодичности контроля при заданной вычислительной мощности средств автоматизации.

Технический результат достигается тем, что оценивают условия функционирования объекта контроля, определяют интенсивность отказов, задают в качестве элементов исходных данных множество периодических аппроксимирующих функций, задают пределы и шаг изменения параметров аппроксимирующих функций, при оценке условий функционирования формируют множество данных о времени и характере воздействия различных дестабилизирующих факторов, фиксируют значения параметров дестабилизирующих факторов, разделяют их на однородные группы, аппроксимируют значения параметров процессов с учетом дестабилизирующих факторов, дополнительно задают алгоритмы вычисления аппроксимирующих функций, вычисляют минимально возможную для заданных исходных данных точность аппроксимации, измеряют минимальное время вычисления аппроксимирующей функции, записывают в память ЭВМ результаты измерения, выделяют аппроксимирующую функцию с минимальным временем вычисления, выбирают алгоритм по критерию использования минимального объема памяти, используемой в процессе вычисления алгоритма, вычисляют период следования аппроксимирующей функции, вычисляют значение частоты полученной функции для определения оптимальной периодичности контроля.

Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественные всем признакам заявленного решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности "новизна". Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного способа, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность влияния предусматриваемых существенными признаками заявленного изобретения преобразований на достижение указанного технического результата. Следовательно, заявленное изобретение соответствует условию патентоспособности "изобретательский уровень".

Заявленный способ поясняется чертежами, на которых показаны:

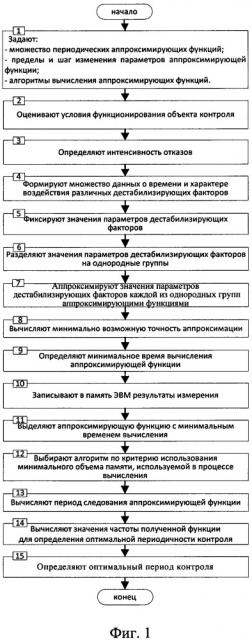
фиг. 1 - блок-схема алгоритма способа определения оптимальной периодичности контроля состояния технических средств и систем;

фиг. 2 - пример аппроксимации интеграла левыми прямоугольниками;

фиг. 3 - пример аппроксимации интеграла правыми прямоугольниками;

фиг. 4 - рисунок, поясняющий вычисление точности аппроксимации.

Заявленный способ базируется на теореме Котельникова [Баскаков С.И. Радиотехнические цепи и сигналы. М.: Высшая школа, 2-е издание. - 446 с, стр. 116-117, Теория передачи сигналов: Учебник для вузов / Зюко А.Г., Кловский Д.Д., Назаров М.В., Финк Л.М. - М.: Связь, 1980. - 288 с., стр. 68]. Согласно данной теореме произвольный сигнал, спектр которого не содержит частот выше ƒ_в, может быть полностью и однозначно восстановлен, если известны отсчетные значения этого сигнала, взятые через равные промежутки времени 1/(2ƒ_в).

То есть если контроль будет проводиться через промежутки времени, равные отношению T_контр=1/(2ƒ_в), то значения параметров контролируемого процесса могут быть однозначно восстановлены на заданном интервале времени.

Заявленный способ может быть реализован следующим образом (Фиг. 1):

Предварительно задают в качестве исходных данных (бл. 1 фиг. 1):

- множество периодических аппроксимирующих функций;

- пределы и шаг изменения параметров аппроксимирующих функций;

- алгоритмы вычисления аппроксимирующих функций.

Далее для определения частоты ƒ_в оценивают условия функционирования объекта контроля (бл. 2 фиг. 1).

На следующем этапе определяют интенсивность отказов объекта контроля (бл. 3 фиг. 1).

Интенсивность отказов - условная плотность вероятности возникновения отказа объекта, определяемая при условии, что до рассматриваемого момента времени отказ не возникает [ГОСТ 27.002-89. Межгосударственный стандарт. Надежность в технике. Основные понятия. Термины и определения]. Способы определения интенсивности отказов известны и представлены, например, в [ГОСТ Р МЭК 60605-6 - 2007 г. Критерии проверки постоянства интенсивности отказов и параметра потока отказов; B.C. Деев, В.А. Трефилов. Надежность технических систем и техногенный риск. Учеб. пособие / B.C. Деев, В.А. Трефилов. Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2012. 180 с.; Расчет показателей надежности радиоэлектронных средств: учеб-метод. Пособие / С.М. Боровиков, И.Н. Цырельчук, Ф.Д. Троян; под ред. С.М. Боровикова. - Минск: БГУИР, 2010. - 68 с.].

Далее формируют множество данных о времени и характере воздействия различных дестабилизирующих факторов (бл. 4 фиг. 1).

Например, дестабилизирующим фактором для сети электросвязи является физический или технологический процесс внутреннего или внешнего по отношению к сети электросвязи характера, приводящее к выходу из строя элементов сети [ГОСТ Р 53111-2008: Устойчивость функционирования сети связи общего пользования. Требования и методы проверки].

Согласно [ГОСТ Р 53111-2008: Устойчивость функционирования сети связи общего пользования. Требования и методы проверки] воздействия дестабилизирующих факторов на сети электросвязи разделяется на воздействие внутренних и внешних дестабилизирующих факторов.

Под внешними дестабилизирующими факторами по отношению к сети электросвязи понимаются такие дестабилизирующие факторы, источники которых расположены вне сети электросвязи.

В зависимости от характера воздействия на элементы сети электросвязи внешние дестабилизирующие факторы делятся на классы:

- механические (сейсмический удар, ударная волна взрыва, баллистический удар);

- электромагнитные (низкочастотное излучение, высокочастотное излучение, сверхвысокочастотное излучение, электромагнитный импульс);

- ионизирующие (альфа-излучение, бета-излучение, гамма-излучение, нейтронное излучение);

- термические (световое излучение взрыва).

Под внутренними дестабилизирующими факторами по отношению к сети электросвязи понимаются дестабилизирующие факторы, источники воздействия которых находятся внутри сети электросвязи и имеется достаточная информация о характеристиках их воздействий, позволяющая принимать эффективные решения по их локализации и проведению соответствующих профилактических и ремонтно-восстановительных мероприятий на всех этапах, от разработки и производства средств электросвязи до проектирования и эксплуатации сетей электросвязи.

Наиболее распространенными источниками внутренних дестабилизирующих факторов являются:

- качество электрических контактов;

- старение электрорадиоэлементов (изменение со временем их характеристик);

- нарушение электромагнитной совместимости (нарушение экранирования, заземлений, фильтрации) и, вследствие этого, ухудшение устойчивости оборудования электросвязи к воздействию электромагнитных помех;

- перебои в электроснабжении.

Фиксируют значения параметров дестабилизирующих факторов (бл. 5 фиг. 1).

Например, для сейсмической волны (механические внешние дестабилизирующие факторы) в качестве параметров выступают: амплитуда волны, ее скорость (ускорение), продолжительность импульса (число фаз в импульсе) и т.д. [Геологический словарь, т. 2. М.: Недра, 1973. - 456 с., стр. 135].

Основными параметрами электромагнитного импульса (электромагнитные внешние дестабилизирующие факторы) являются изменения напряженностей электрического и магнитного полей во времени (форма импульса) и их ориентация в пространстве, а также величина максимальной напряженности поля (амплитуда импульса) [Электромагнитный импульс. Электронный ресурс www://http://gochs.info/p0967.htm. Дата последнего обращения 08.12.2015; Лоборев В.М. (ред.) Физика ядерного взрыва. Том 1. М.: Наука, 1997. - 528 с, стр. 85-120], основными параметрами электромагнитных излучений -частота, напряженность электрического и магнитного полей [Богуш В.А., Торботько Т.В., Гусинский А.В и др. Электромагнитные излучения методы и средства защиты. Под ред. Л.М. Лынькова. - Мн.: Бестпринт, 2003. - 406 с., стр. 11-54] и т.д.

Далее параметры дестабилизирующих факторов разделяют на однородные группы (бл. 6 фиг. 1).

Однородность - тождественность объекта, множества объектов во всей области определения [В.Н. Савченко, В.П. Смагин. Начала современного естествознания. Тезаурус. - Ростов-на-Дону. 2006].

Полученные значения параметров каждой из выделенных однородных групп А_i, …, A_j аппроксимируют непрерывными периодическими функциями (например, простыми гармоническими кривыми вида y=Asin(ω₀t+φ), y=Acos(ω₀t+φ), где А - амплитуда колебания, ω₀ - круговая (циклическая) частота, φ - начальная фаза колебания [В.И. Смирнов Курс высшей математики, Т. 1.: Изд-во "Наука". 1974. - 479 с., стр. 43-48; Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974 г. - 592 с., стр. 273-338] и др., удовлетворяющими заданным требованиям (бл. 7 фиг. 1)).

Согласно [Савельев И.В. Курс общей физики, т. 1. Механика. Молекулярная физика: Учебное пособие. - 2-е изд., перераб. - М.: Наука. Главная редакция физико-математической литературы, 1982. - 432 с., стр. 190-195], поскольку косинус (синус) - периодическая функция с периодом 2π, ее период Т может быть определен как Т=2π/ω₀.

Аппроксимация - это представление сложных функций s(x) или дискретных выборок из этих функций s(x_i) простыми и удобными для практического использования функциями аппроксимации ƒ(х) таким образом, чтобы отклонение ƒ(х) от s(x) в области ее задания было наименьшим по определенному критерию приближения [Давыдов А.В. Цифровая обработка сигналов. Лекции и практикум на ПК. Тема 14. Аппроксимация сигналов и функций. Электронный ресурс: www//http://geoin.org/. Дата обращения: 10.09.2017.]

Вычисляют минимально возможную для заданных исходных данных точность аппроксимации функции (бл. 8 фиг. 1, фиг. 4) путем пошагового вычисления ее значения до минимального, пока не произойдет увеличение ее значения, следовательно, число шагов равно N=N-1/2N. Шаг N должен быть равен или меньше значения отклонения при округлении в точке аппроксимации.

Далее из исходных данных выбирают алгоритм вычисления аппроксимирующей функции, имеющий минимальную сложность, а именно вычислительную сложность и сложность алгоритма по памяти.

Алгоритм - это точное предписание, однозначно определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату. Выбор алгоритма существенно влияет на сложность вычисления задачи. Сложность вычисления есть функция, дающая числовую оценку трудоемкости применения алгоритма к исходным данным для получения искомого результата

При выборе алгоритмов очень важно иметь возможность оценить ресурсы, необходимые для проведения вычислений. Результатом оценки является функция сложности (трудоемкости). Оцениваемым ресурсом чаще всего является процессорное время (вычислительная сложность) и память (сложность алгоритма по памяти). Оценка позволяет предсказать время выполнения и сравнивать эффективность алгоритмов. [Васильев В.С. Алгоритм. Свойства алгоритма [Электронный ресурс] - режим доступа: https://pro-prof.com/archives/578. Дата обращения: 10.09.2017.].

Например, интеграл можно понимать как площадь фигуры, размещенной под графиком функции. Существует ряд методов аппроксимации (приближенного вычисления) интеграла, к ним относится, в частности, метод прямоугольников. Площадь под графиком делится на множество прямоугольников и приближенно вычисляется как сумма их площадей. Следовательно, возможен переход от интеграла к сумме и наоборот.

На фиг. 2, 3 приведен пример аппроксимации функции fx=logx левыми и правыми прямоугольниками. Очевидно, они дадут верхнюю и нижнюю оценку площади под графиком:

для возрастающих функций;

для убывающих функций.

В частности, такой метод позволяет оценить алгоритмы, имеющие логарифмическую сложность (две последние формулы суммирования). [Васильев В.С. Алгоритм. Свойства алгоритма [Электронный ресурс] - режим доступа: https://pro-prof.com/archives/578. Дата обращения: 10.09.2017.].

Для оценки временной сложности алгоритма определяют минимальное время вычисления аппроксимирующей функции при минимальной точности аппроксимации (бл. 9 фиг. 1).

Измерение времени вычисления аппроксимирующей функции может получено на основе теории сложности вычислений [Гери М., Джонсон Д. Вычислительные машины и труднорешаемые задачи. Издательство Мир в 1982 год. - 420 с.] - раздел теории вычислений, изучающий объем работы, требуемой для решения вычислительной проблемы.

Время вычисления описывается произведением числа шагов алгоритма от исходных данных до искомого результата и средним физическим временем реализации одного шага. Число шагов определяется описанием алгоритма в заданной алгоритмической модели.

Пусть машина Тьюринга [Люстерник Л.А., Червоненкис О.А., Янпольский А.Р. Математический анализ: Вычисление элементарных функций. - М.: Физматгиз, 1963. - 248 с. Попов Б.А., Теслер Г.С. Вычисление функций на ЭВМ: Справочник. - Киев: Наукова думка, 1985. - 600 с.] вычисляет некоторую функцию f(x) данного класса задач. Тогда t(x) есть функция, равная числу шагов при вычислении f(x), если f(x) определена. Функция t(x) называется временной сложностью. Однако физическое время реализации одного шага алгоритма на конкретном компьютере зависит от типа компьютера, способов компиляции, скорости обработки информации, что существенно усложняет определение временной сложности.

Чаще всего временную сложность t(x) описывают полиномами от исходных данных. Если известен размер исходных данных - |х| и временная сложность задана некоторым полиномом t(|x|)=р(|х|), то оценка временной сложности есть O(р(|х|)). Эта оценка определяется, как правило, старшим членом полиномиального ряда. При этом говорят, что машина Тьюринга решает задачу за полиномиальное время. Например, если временная сложность задана полиномом р(|х|)=4|х|2+7|х|+12, то оценка временной сложности есть O(|х|2). Алгоритм, имеющий полиномиальное время, называют полиномиальным алгоритмом. Множество однотипных задач, разрешаемых на машине Тьюринга за полиномиальное время, принадлежит классу задач Р (polynomial) [Люстерник Л.А., Червоненкис О.А., Янпольский А.Р. Математический анализ: Вычисление элементарных функций. - М.: Физматгиз, 1963. - 248 с. Попов Б.А., Теслер Г.С. Вычисление функций на ЭВМ: Справочник. - Киев: Наукова думка, 1985. - 600 с.].

Записывают в память ЭВМ результаты измерения (бл. 10 фиг. 1).

Выделяют аппроксимирующую функцию с минимальным временем вычисления (бл. 11 фиг. 1)

Далее выбирают алгоритм по критерию использования минимального объема памяти, используемой в процессе вычисления алгоритма (бл. 12 фиг. 1). Объем памяти как количественная характеристика алгоритма определяется количеством единиц памяти, используемых в процессе вычисления алгоритма. Эта величина не может превосходить максимального числа единиц памяти, используемых на одном шаге алгоритма.

Пусть машина Тьюринга вычисляет функцию f(x). Тогда s(x) есть функция, равная множеству всех ячеек информационной ленты, которые, если f(x) определена, посещаются в процессе вычисления этой функции. Функция s(x) называется емкостной сложностью.

Если машина Тьюринга имеет внешнюю и внутреннюю памяти мощности n=|Vt| и m=|Q| соответственно, то для временной и емкостной функций сложности допустимы оценки:

s(x)£|х|+t(x),

t(x)£m*s2(x)|ns(x)

После определения всех аппроксимирующих функций для получения значений частоты полученной функции, вычисляют период следования аппроксимирующей функции (бл. 13 фиг. 1).

Период функции - длина интервала повторения. Если период следования аппроксимирующей функции разный, то вычисляют средний период следования аппроксимирующей функций.

Вычисляют значение частоты полученной функции для определения оптимального периода контроля.

Число колебаний в единицу времени называется частотой колебания ƒ. Частота ƒ связана с продолжительностью одного колебания Т следующим соотношением: ƒ=1/Т (бл. 14 фиг. 1).

Согласно выражению T_контр=1/(2ƒ_в) определяют оптимальный период контроля в условиях воздействия различных дестабилизирующих факторов.

Таким образом, благодаря новой совокупности существенных признаков за счет определения минимальной возможной точности аппроксимации для заданных исходных данных и определения алгоритма с минимальной временной и емкостной сложностью в заявленном способе обеспечивается достижение технического результата, а именно сокращение времени определения оптимальной периодичности контроля при заданной вычислительной мощности средств автоматизации.

Способ определения оптимальной периодичности контроля состояния технических средств и систем при минимальном времени получения результата, заключающийся в том, что оценивают условия функционирования объекта контроля, определяют интенсивность отказов, задают в качестве исходных данных множество периодических аппроксимирующих функций, задают пределы и шаг изменения параметров аппроксимирующих функций, при оценке условий функционирования формируют множество данных о времени и характере воздействия различных дестабилизирующих факторов, фиксируют значения параметров дестабилизирующих факторов, разделяют их на однородные группы, аппроксимируют значения параметров дестабилизирующих факторов каждой из однородных групп аппроксимирующими функциями, определяют оптимальный период контроля, отличающийся тем, что дополнительно задают алгоритмы вычисления аппроксимирующих функций, вычисляют минимально возможную для заданных исходных данных точность аппроксимации, определяют минимальное время вычисления аппроксимирующей функции при минимальной точности аппроксимации, записывают в память ЭВМ результаты измерения, выделяют аппроксимирующую функцию с минимальным временем вычисления, выбирают алгоритм по критерию использования минимального объема памяти, используемой в процессе вычисления алгоритма, вычисляют период следования аппроксимирующей функции, вычисляют значение частоты полученной функции для определения оптимального периода контроля.