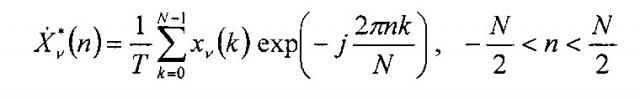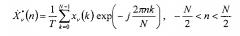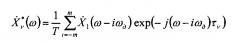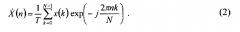Способ дискретизации и восстановления непрерывного сигнала

Способ дискретизации и восстановления непрерывного сигнала

Иллюстрации

Показать все

Реферат

Изобретение относится к области измерительной техники и предназначено для использования в системах контроля окружающей среды и технологических процессов.

Известен способ дискретизации и восстановления непрерывных сигналов с ограниченным спектром, вытекающий из теоремы Котельникова [Котельников В.Л. О пропускной способности эфира и проволоки в электросвязи. Материалы к 1-му Всесоюзному съезду, ВЭК, 1933, Харкевич А.А. Спектры и анализ. Издание четвертое. Изд. ФМЛ. - М., 1962. - 236 с.].

По этому способу цифровые отсчеты непрерывного сигнала берут с частотой, в два раза превышающей верхнюю граничную частоту в спектре сигнала, а восстанавливают по интерполяционной формуле (ряду Котельникова), содержащей бесконечную сумму взвешенных по функциям sin x/x отсчетов.

Этот способ принят в качестве прототипа. К недостаткам прототипа можно отнести следующее.

Сигналы с ограниченным спектром используются только в технических системах. Реальные непрерывные сигналы от естественных источников окружающей среды обычно имеют бесконечный, хотя и затухающий, спектр. Если допустим определенный уровень погрешности при восстановлении сигнала, возможно ограничение бесконечного спектра некоторой частотой среза. Если это ограничение до половины частоты дискретизации не производится низкочастотной фильтрацией перед дискретизацией, то возникает известное явление наложения частот (апиасинг), приводящее к не устраняемой составляющей погрешности дискретизации при восстановлении непрерывного сигнала любыми временными интерполяторами, в том числе и рядом Котельникова [Ж. Макс. Методы и техника обработки сигналов при физических измерениях: В 2-х т. Пер. с франц. - М.: Мир, 1983. - Т.1. - 312 с.].

В системах циклического контроля окружающей среды (например, зондированием прибором толщи океана, полигонной съемкой региона последовательным обходом станций и т.д.) возможности низкочастотной фильтрации процессов и полей обычно ограничены или она в принципе не возможна. Одновременно ограничена сверху и частота временной дискретизации экономическими затратами или возможностями практической peaлизации. В этих случаях, когда возможности низкочастотной фильтрации и повышения частоты дискретизации исчерпаны, при априорно известных типовых бесконечных спектрах непрерывных сигналов можно оценить возникающую погрешность дискретизации от алиасинга [Гайский В.А., Гайский П.В. Погрешности дискретизации случайных многомерных полей со степенными спектрами. Морской гидрофизический журнал, №6, 1994]. Если эта погрешность оказывается выше допустимого уровня, то нет известных способов ее уменьшения.

Предлагаемый способ решает эту задачу.

Целью предлагаемого изобретения является снижение погрешности дискретизации, обусловленной алиасингом, путем определения параметров гармоник частот наложения и восстановления непрерывного сигнала по спектру в расширенной полосе частот.

Эта цель достигается тем, что при дискретизации сигнала x(t), максимальная значимая частота в спектре которого в m раз превышает половину частоты дискретизации цифровые отсчеты сигнала берут пакетами по m отсчетов с задержками τ_ν от первого и интервалом времени Т между пакетами, последовательности отсчетов регистрируют или передают в канал связи, при восстановлении непрерывного сигнала из последовательности с N пакетами отсчетов формируют m последовательностей {x_ν(k)} с N одиночными отсчетами, (m-1) которых задержаны на интервал от первой дискретным преобразованием Фурье вычисляют спектр с алиасингом каждой из последовательностей {x_ν(k)} по формуле

,

для каждой из частот неизвестного спектра сигнала формируют суммы взвешенных задержками гармоник частот наложения по уравнению

,

где ,

при из последнего уравнения формируют систему с неизвестными при -m<i<m, решением системы уравнений находят неизвестные составляющие расширенного спектра исходного процесса восстанавливают непрерывный сигнал x(t) обратным преобразованием Фурье по формуле

.

Изобретение поясняется рисунками.

На фиг. 1 показаны схемы равномерной (а) и равномерной пакетной (б) дискретизации непрерывного сигнала мгновенными отсчетами, на фиг. 2 представлена схема алиасинга для положительных (ω) и отрицательных (-ω) частот, фиг. 3 иллюстрирует схему формирования рядов задержанных одиночных отсчетов, на фиг. 4 показаны, для примера, графики спектров и функций модуляции для пакета из 5 отсчетов с кратными задержками, на фиг. 5 показан график вертикального зондирования верхнего слоя моря непрерывного (1) и с остановками на некоторых горизонтах (2), на фиг. 6 представлен график выполнения циклического обхода станций гидрологического полигона с одним (1) и несколькими (2) зондированиями на станциях.

Суть предлагаемого способа дискретизации мгновенными отсчетами и восстановления непрерывного сигнала по этим отсчетам состоит в следующем.

Предполагается, что непрерывный процесс x(t) на отрезке времени TN с достаточной точностью представляется ограниченным частотой Ω_c спектром

Таким образом, если известно то по выражению (1) можно восстановить x(t) с достаточной точностью.

После дискретизации сигнала x(t) рядом {х(k)} (фиг. 1а) из N отсчетов с интервалом Т его спектр определяется дискретным преобразованием Фурье [Сергиенко А.Б. Цифровая обработка сигналов: Учебник для вузов. 2-е изд. - Спб.: Питер, 2006. - 751 с.: ил.]

Если частота дискретизации то алиасинга нет, дискретный спектр не содержит частот наложения и непрерывный сигнал x(t) восстанавливается по интерполяционной формуле Котельникова или тригонометрическим рядом Фурье.

Если с то имеет место алиасинг и вычисляемые в рабочей полосе частот спектральные составляющие содержат суммы гармоник частот наложения в соответствии с известной формулой

где

Эта формула наглядно иллюстрируется «пилой» алиасинга на фиг. 2, где горизонтальная ось соответствует шкале частот ω или Ω, а вертикальная ось направлением вниз соответствует шкале частот рабочей полосы

Для каждой частоты ω в рабочей полосе частоты гармоник наложения определяется точками пересечения горизонтальной прямой, проходящей через эту частоту на вертикальной оси с «пилой» алиасинга так, как это показано на фиг. 2.

Для нахождения спектральных составляющих необходимо придать им вес и сформировать дополнительные уравнения, это обеспечивается задержками.

Поскольку спектр сигнала умножается на при задержке сигнала x(t)

на τ_ν, то при дискретизации берут пакет из т отсчетов с задержками от первого (фиг. 1б). При восстановлении формируют m отдельных ν, k последовательностей {x_ν(k)} с единичными отсчетами, интервалом дискретизации Т и сдвигами (фиг. 3).

Для каждой ν-й последовательности {x_ν(k)} вычисляют дискретный спектр

и записывают уравнение с наложением частот, аналогичное выражению (3),

При этом наложение частот происходит с модуляцией функцией G_ν(ω), графики для вещественных и для мнимых составляющих которой, показаны на фиг. 4, для примера, из 5 отсчетов с кратными задержками.

Для каждой ω формируют из выражения (5) при систему линейных алгебраических уравнений с неизвестными спектральными компонентами исходного непрерывного процесса x(t), расширенные матрицы которых имеют вид

для ω

для ω

Решением систем (6) и (7) находят компоненты расширенного спектра исходного сигнала, которых стало mN вместо N, что эквивалентно увеличению частоты дискретизации в m раз.

Используя обратное преобразование Фурье, восстанавливают непрерывный сигнал x(t) по конечному ряду со сколь угодно высоким временным разрешением по формуле

содержащей конечное число членов, в отличие от формулы Котельникова.

Таким образом, для реализации предложенного способа дискретизации и восстановления непрерывного сигнала необходимо обеспечить дискретизацию пакетами. При этом общее число отсчетов равно числу отсчетов при увеличении частоты дискретизации в m раз.

Рассмотрим примеры использования способа.

В многоканальных системах аналого-цифрового преобразования с одним аналого-цифровым преобразователем и коммутатором на N каналов время цикла равно (период дискретизации одного сигнала) (фиг. 1а)

,

где τ_k - время коммутации одного канала;

τ_n - время одного аналого-цифрового преобразования. Если τ_n<τ_k, τ_n=ατ_k, α<1, что характерно при использовании квазиследящих или сигма-дельта АЦП, то для повышения быстродействия целесообразно использовать пакетную дискретизацию (фиг. 1б). В этом случае при m отсчетах в пакете эквивалентная частота дискретизации возрастает в m раз, но и период опроса возрастает и будет равен

Выгрыш в увеличении эквивалентной частоты дискретизации составит

Следовательно, при реальных значениях времен преобразования и коммутации предложенный способ пакетной дискретизации и восстановления дает выигрыш в эквивалентной частоте дискретизации.

В океанографии контроль морской среды осуществляется путем выполнения с помощью экспедиционного судна повторяющегося полигона станций с вертикальным зондированием верхнего слоя моря и измерениями по траектории зонда. График такого зондирования показан на фиг. 5(1). Если выполняется одно зондирование на станции, то частота временной дискретизации каждой точки среды на фиксированной глубине составит где T₁ - периодичность съемок, которая в лучшем случае не будет меньше времени выполнения полигона. Это время фактически составляет время сканирования пространства, поскольку измерения выполняются параллельно и, в принципе, время одного измерения может быть существенно меньше времени перемещения между двумя точками пространства на расстояние требуемого шага пространственной дискретизации.

Если озаботиться при этом эквивалентной частотой временной дискретизации в конкретных точках пространства (например, на «стандартных» горизонтах гидрологической станции), то это можно выполнить с использованием предложенного способа дискретизации и восстановления непрерывного сигнала путем реализации пакета отсчетов в этих точках при остановке зонда на стандартных горизонтах (фиг. 5) или выполнением нескольких зондирований на каждой станции полигона (фиг. 6).

На фиг. 5 показаны графики многократного зондирования верхнего слоя моря непрерывного (1) и с остановками на некоторых горизонтах (2). В первом случае измерение в каждой точке осуществляется при движении вниз параллельно с движением зонда и затрат времени на него нет. Время между отсчетами равно τ₃ и частота дискретизации равна Для выбранного числа горизонтов g (например, при принятых в гидрологии стандартных глубин g=16) возможно увеличение эквивалентной частоты дискретизации, если осуществить остановку зонда на этих горизонтах для взятия пакета из m измерений за время При этом период дискретизации будет равен а эквивалентная частота дискретизации будет равна при α<<1. Выигрыш в эквивалентной частоте дискретизации составит

Таким образом, практически всегда возможно использовать предлагаемый способ дискретизации и восстановления непрерывного сигнала на выбранных горизонтах океанографической станции для расширения полосы рабочих частот.

Второй пример использования предложенного способа при океанографической съемке путем циклического обхода станций полигона с непрерывным зондированием на станциях одним (1) и несколькими зондированиями (2) показан на фиг. 6.

При этом период дискретизации с одним зондированием составит с m зондированиями - , где - время перехода между станциями; обычно α<1.

Выигрыш в эквивалентной частоте дискретизации составит

Эта формула аналогична формуле (9), поэтому выводы (10) для нее справедливы.

Способ дискретизации и восстановления непрерывного сигнала x(t) с использованием его цифровых отсчетов через равные интервалы времени Т, отличающийся тем, что при дискретизации отсчеты берут пакетами по m отсчетов с задержками от первого, последовательность из N пакетов отсчетов регистрируют или передают в канал связи, при восстановлении из последовательности с пакетами отсчетов формируют m последовательностей одиночных отсчетов {х(k)}, задержанных на интервал времени τ_ν(τ₁=0) от первой, дискретным преобразованием Фурье, вычисляют спектр с алиасингом каждой из последовательностей {x_ν(k)} по формуле

где

для каждой из частот неизвестного спектра формируют суммы взвешенных задержками гармоник частот наложения по уравнению

где

из которого формируют систему линейных алгебраических уравнений относительно неизвестных составляющих гармоник (-m≤i≤m), решением системы определяют неизвестные, обратным преобразованием Фурье восстанавливают непрерывный сигнал x(t) по формуле