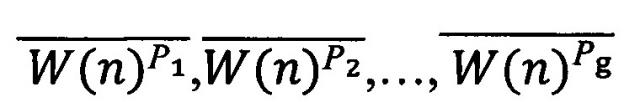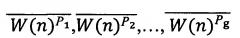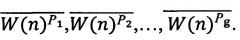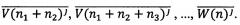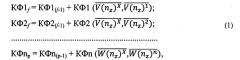Способ быстрого декодирования информационных элементов сигнала

Способ быстрого декодирования информационных элементов сигнала

Иллюстрации

Показать все

Реферат

Изобретение относится к области радиосвязи и может найти применение в системах, в которых используются широкополосные сигналы (ШПС). Одним из важных свойств ШПС является обеспечение высокой помехоустойчивости, обусловленной тем, что при свертке ШПС отношение сигнал/помеха увеличивается. Это увеличение тем больше, чем больше база сигнала. За счет выбора большой базы ШПС удается обрабатывать сигнал, который значительно меньше помех. Но чем больше база сигнала, тем больше времени необходимо для его декодирования, а значит хуже пропускная способность канала связи. В связи с этим становиться актуальной разработка способов сокращения этого времени без ущерба для помехоустойчивости канала связи.

В основе известных способов передачи информации с помощью ШПС (RU 125724 U1, дата публикации 10.03.2013; RU 2532085 С2, дата публикации 27.10.2014; RU 2543514 С2, дата публикации 10.03.2015; RU 2587474 С1, дата публикации 20.06.2016; RU 2609525 С1, дата публикации 02.02.2017) лежит кодирование на передающей стороне передаваемой двоичной информации последовательностями Уолша, представленными, например, в виде строк матрицы Адамара порядка n и их декодирование на приемной стороне.

Кодировка состоит в разбиении передаваемой двоичной информации на группы из k бит, где k определяется из соотношения n=2^k. Каждая группа бит определяет информационный элемент и воспринимается в качестве числа P_i, т.е. передаваемая двоичная информация представляется числами Р₁, Р₂, …, P_g. Каждое из этих чисел воспринимается как номер строки в матрице Адамара порядка n.

Последовательностями модулируется, например, фаза несущей частоты информационных элементов сигнала. Таким образом, представленная в двоичном виде информация оказывается закодированной последовательностями

На приемной стороне после обнаружения сигнала осуществляется демодуляция сигнала, дискретизация огибающей, выделение оцифрованных элементов сигнала длиной n и их декодирование.

Выделяется первый информационный элемент сигнала - последовательность из n оцифрованных значений сигнала. Вычисляются корреляционные функции (КФ) последовательности со всеми последовательностями (здесь и далее j=1, 2, n).

Максимальное значение КФ будет достигнуто с последовательностью Номер этой последовательности принимается в качестве числа P₁. Далее выделяется второй информационный элемент сигнала - последовательность из n следующих оцифрованных значений сигнала, вычисляются КФ последовательности со всеми последовательностями Максимальное значение КФ будет достигнуто с последовательностью Номер этой последовательности принимается в качестве числа Р₂.

Повторяя описанный способ декодирования g раз (по количеству информационных групп), будут получены все числа Р₁, Р₂, …, P_g. Из двоичных номеров этих чисел операцией конкатенации формируется двоичное представление передаваемой информации.

Описанный способ декодирования информационных элементов является традиционным. Он занимает много времени, т.к. по указанным выше причинам база сигналов n выбирается достаточно большой.

Технический результат предлагаемого технического решения - уменьшение времени декодирования.

Для этого предлагается способ быстрого декодирования информационных элементов сигнала, закодированных последовательностями Уолша, представленных строками матрицы Адамара порядка n (последовательностями состоящий в том, что на принимающей стороне база последовательностей n представляется в виде n=n₁+n₂+…+n_z+n_g бит, и декодирование неизвестной последовательности начинается с помощью последовательности и последовательностей полученных из ƒ=n₁ бит соответствующих последовательностей и и, после определения номера P₁ последовательности , устанавливается его правильность путем вычисления корреляционной функции (КФ) последовательности с последовательностью и, в случае превышения полученного значения КФ заданного порога, число P₁ считается вычисленным правильно и декодирование считается выполненным, в противном случае декодирование неизвестной последовательности осуществляется с помощью последовательности и последовательностей полученных из ƒ=n₁+n₂ бит соответствующих последовательностей и и, после определения номера Р₂ последовательности устанавливается его правильность путем вычисления корреляционной функции КФ последовательности с последовательностью и, в случае превышения полученного значения КФ заданного порога, число Р₂ считается вычисленным правильно и декодирование считается выполненным, в противном случае декодирование неизвестной последовательности осуществляется с помощью последовательности и последовательностей полученных из ƒ=n₁+n₂+…+n_z бит соответствующих последовательностей и и, после определения номера P_z последовательности , устанавливается его правильность путем вычисления корреляционной функции КФ последовательности с последовательностью и, в случае превышения полученного значения КФ заданного порога, число P_z считается вычисленным правильно и декодирование считается выполненным, в противном случае декодирование неизвестной последовательности осуществляется после очередного увеличения количества ƒ бит последовательностей и декодированием последовательности , определением номера Р_ƒ и его правильности до тех пор, пока не будет получено правильное значение номера Р_ƒ при ƒ=n.

В основе предлагаемого способа быстрого декодирования последовательности лежат следующие действия.

Действие 1

Вычисление корреляционной функции КФ может быть осуществлено по частям.

Разбиваем число бит n на группы так, что n=n₁+n₂+…+n_z+…+n_m.

Последовательности, содержащие только биты n₁, или только биты n₂, …, или только биты n_m, обозначим, соответственно, как Последовательности, содержащие только биты (n₁+n₂), или только биты (n₁+n₂+n₃), …, (n₁+n₂+…+n_z+…+n_m)=n обозначим, соответственно, как

В этих обозначениях корреляционные функции последовательностей и для ƒ=n₁+n₂+…+n_z вычисляются как:

где (ƒ-1)=n₁+n₂+…+n_z-1 бит.

Действие 2

Каждая последовательность с базой n=2^k может быть однозначно определена всего по k битам, где k - показатель двойки в порядке n матрицы Адамара, а номера этих бит можно вычислить по формуле:

где h=1, 2, …, k.

Остальные биты являются второстепенными и предназначены для повышения помехоустойчивости сигнала. Учитывая это, в матрице Адамара порядка n во всех последовательностях все, вычисленные по формуле (2) биты, переставляются вперед и при разбиении базы на части n=n₁+n₂+…+n_z+…+n_m включаются в состав бит n₁.

Такая перестановка не нарушает свойств строк матрицы Адамара, но позволяет однозначно идентифицировать последовательность по битам n₁, или по битам (n₁+n₂), …, или по битам (n₁+n₂+…+n_z)…, или по битам n.

Действие 3

Известно, что отношение сигнал/помеха на входе коррелятора ρ² и на его выходе h² связаны соотношением:

где В - база сигнала (число бит n последовательностей Из (3) следует, что при отношении сигнал/помеха на входе коррелятора, равном всегда можно подобрать такое значение базы B_i, при котором величина обеспечит правильное декодирование информационных элементов сигнала с заданной вероятностью. На практике база сигнала n выбирается в соответствии с минимально допустимым отношением сигнал/помеха т.е. большей, чем это требуется при отношениях сигнал/помеха А, так как помеховая обстановка с максимальной помехой действует на ШПС достаточно редко, то при для декодирования сигнала с заданной вероятностью достаточно было бы иметь сигнал с базой, меньшей n, т.е. сигнал с базой n₁, или сигнал с базой (n₁+n₂), или сигнал с базой (n₁+n₂+n₃) и т.д.

Действие 4

Как было описано выше, при декодировании n оцифрованных значений сигнала вычисляются корреляционные функции КФ и среди вычисленных значений определяется максимальное. Однако такой возможности нет при декодировании последовательности по n₁ битам, или по (n₁+n₂) битам, и т.д.

В предлагаемом способе быстрого декодирования критерий «максимальное значение корреляционной функции» заменен на критерий «превышение значения корреляционной функции порога П_i». Значения порогов П_i для разных и разного количества бит ƒ можно подобрать при настройке изделия или заранее определить путем моделирования.

С учетом перечисленных действий способ быстрого декодирования последовательностей Уолша, обеспечивающий сохранение требуемой помехоустойчивости, можно изложить следующим образом.

Количество бит n последовательностей разбивается на группы n=n₁+n₂+…+n_z+…+n_m.

В соответствии с Действием 2 для выбранной базы сигнала n=2^k определяется количество бит k и с помощью формулы (2) определяются номера бит, которые однозначно определяют последовательности Вычисленные по формуле (2) биты переставляются во всех последовательностях вперед так, чтобы они попали в группу n₁.

Вычисляются корреляционные функции КФ последовательности со всеми последовательностями , где ƒ=n₁ бит. Номер последовательности обеспечившей максимум КФ, принимается в качестве предположительной оценки передаваемого числа P₁. Для подтверждения этого предположения вычисляется КФ и полученное значение сравнивается с порогом Если значение КФ превысило порог (отношение сигнал/помеха на входе коррелятора таково, что количества бит n₁ последовательностей и достаточно для правильного декодирования последовательности , то принимается решение, что число P₁ определено правильно, и декодирование последовательности по количеству бит n₁ считается выполненным. Время декодирования последовательности по количеству бит n₁ будет много меньше времени декодировании традиционным способом (по количеству бит n).

Если же значение КФ не превысило порог (отношение сигнал/помеха на входе коррелятора таково, что количества бит n₁ последовательностей и недостаточно для правильного декодирования последовательности то необходимо увеличить базу последовательностей и

Далее вычисляются значения КФ которые в соответствии с Действием 1 складываются с уже вычисленными значениями КФ , Получатся корреляционные функции КФ , где ƒ=n₁+n₂ бит. Номер последовательности давшей максимальное значение КФ, предварительно принимается за передаваемое число Р₂. Для подтверждения этого предположения вычисляется КФ и полученное значение сравнивается с порогом . Если значение КФ превысило порог (отношение сигнал/помеха на входе коррелятора таково, что количества бит ƒ=(n₁+n₂) последовательностей и достаточно для правильного декодирования последовательности то принимается решение, что число Р₂ определено правильно. Время декодирования последовательности по количеству бит ƒ=(n₂+n₂) будет много меньше времени декодировании традиционным способом (по количеству бит n).

Если же значение КФ не превысило порог (отношение сигнал/помеха на входе коррелятора таково, что количества бит ƒ=(n₁+n₂) последовательностей и недостаточно для правильного декодирования последовательности то необходимо увеличить базу последовательностей и

Увеличение количества бит ƒ и декодирование предлагаемым способом может привести к ситуации, когда ƒ=n. В этом случае число P_n будет определено правильно, однако время декодирования оцифрованных значений сигнала предлагаемым способом будет превышать время выполнения традиционным способом декодирования.

В таблице 1 для базы n=256 приведены оценки увеличения числа алгоритмических операций при вычислении способом быстрого декодирования для разных вариантов разбиения на группы.

Из таблицы 1 видно, что в худшем варианте, когда на входе коррелятора отношение сигнал/помеха будет составлять увеличение числа алгоритмических операций составит не более 17%.

В случаях, когда время декодирования будет существенно меньше. Так, например, для базы n=256 и при разбиении n на 16 одинаковых групп, выигрыш по времени будет: при количестве бит ƒ=n₁, при количестве бит ƒ=2n₁, …, при количестве бит ƒ=14n₁₄. И только при количестве бит ƒ=15n₁₅ и количестве бит ƒ=n будет превышение времени, соответственно, не более, чем на 3% и 9% от времени традиционного декодирования.

Способ быстрого декодирования информационных элементов сигнала, закодированных последовательностями Уолша, представленных строками матрицы Адамара порядка n (последовательностями , состоящий в том, что на принимающей стороне база последовательностей n представляется в виде n=n₁+n₂+...+n_z+n_g бит и декодирование неизвестной последовательности начинается с помощью последовательности и последовательностей полученных из бит соответствующих последовательностей и и, после определения номера P₁ последовательности устанавливается его правильность путем вычисления корреляционной функции (КФ) последовательности с последовательностью и, в случае превышения полученного значения КФ заданного порога, число P₁ считается вычисленным правильно и декодирование считается выполненным, в противном случае декодирование неизвестной последовательности осуществляется с помощью последовательности и последовательностей полученных из бит соответствующих последовательностей и и, после определения номера Р₂ последовательности устанавливается его правильность путем вычисления корреляционной функции КФ последовательности с последовательностью и, в случае превышения полученного значения КФ заданного порога, число Р₂ считается вычисленным правильно и декодирование считается выполненным, в противном случае декодирование неизвестной последовательности осуществляется с помощью последовательности и последовательностей полученных из бит соответствующих последовательностей и и, после определения номера P_z последовательности устанавливается его правильность путем вычисления корреляционной функции КФ последовательности с последовательностью и, в случае превышения полученного значения КФ заданного порога, число P_z считается вычисленным правильно и декодирование считается выполненным, в противном случае декодирование неизвестной последовательности осуществляется после очередного увеличения количества бит последовательностей и декодированием последовательности определением номера и его правильности до тех пор, пока не будет получено правильное значение номера при .