Способ восстановления курсовой ориентации космического аппарата с использованием бесплатформенного орбитального гирокомпаса

Способ восстановления курсовой ориентации космического аппарата с использованием бесплатформенного орбитального гирокомпаса

Иллюстрации

Показать все

Реферат

Изобретение относится к области космической техники и может быть использовано для повышения качества переходного процесса и снижения времени восстановление курсовой ориентации орбитального космического аппарата (КА), в состав системы управления угловым движением (СУД) которого входит орбитальный бесплатформенный гирокомпас (ОГК).

В книге [1] авторов Бесекерского В.А., Иванова В.А., Самотокина Б.Б. «Орбитальное гирокомпасирование». СПб. 251 с. 1993 рассмотрен способ восстановления курсовой ориентации КА с помощью гироорбитанта. Недостатком способа являются большое время восстановления ориентации и низкое качество переходного процесса, выражающееся в большой величине перерегулирования в каналах угловой ориентации КА - порядка 5÷40°.

Аналогичными недостатками обладают все, без исключения, известные типы ОГК, см., например [3-6]. Это связано с тем, что в классическом ОГК восстановление курсовой ориентации осуществляется путем непосредственного включения режима гирокомпасирования, который принципиально не приспособлен к работе в таком режиме. При этом движение КА в сторону устойчивого полюса (плоскость орбиты) происходит слишком долго, некоординированно, с большим перерегулированием. Крайне негативно этот недостаток проявляется в системах управления орбитальных КА с релейным режимом стабилизации.

Наиболее близким аналогом может служить техническое решение, представленное в статье [3] авторов Кэмпбел, Коффи «Цифровые системы отсчета углов». Журнал «Вопросы ракетной техники», 1971 г., №11, стр. 63÷88.

Техническим результатом является повышение качества и существенное уменьшение времени переходного процесса при восстановлении курсовой ориентации КА с применением ОГК бесплатформенного типа.

Для достижения результата в известный способ, включающий приведение КА к местной вертикали по сигналам прибора ориентации по Земле (ПОЗ) и стабилизацию КА относительно ОСК по крену и тангажу по сигналам ПОЗ и гироскопических измерителей угловой скорости (ГИУС) крена и тангажа, а также стабилизацию КА в канале курса по сигналу курсового ГИУС, вводят новые операции - приводят КА к местной вертикали до выполнения условий ⎜γ_ПОЗ⎜≤Δγ, ⎜ϑ_ПОЗ⎜≤Δϑ, где γ_ПОЗ, ϑ_ПОЗ - сигналы ПОЗ по крену и тангажу соответственно, Δγ, Δϑ - заданные погрешности ориентации КА относительно местной вертикали, снимают показания ГИУС об угловых скоростях КА по крену и тангажу и рассчитывают текущее положение КА по курсу относительно ОСК на момент времени, например, по формуле , где ω_Xi, ω_Zi - абсолютные угловые скорость КА в каналах крена и тангажа соответственно, которое запоминают, подключают ПОЗ в контур коррекции ОГК и переходят на стабилизацию КА по сигналам ОГК с одновременным поворотом КА в плоскость орбиты со скоростью , где λ(τ), τ - текущие значения программного угла, программной скорости и времени программного поворота соответственно, в процессе которого компенсируют взаимовлияние каналов ориентации перекрестными связями по аргументу разности начального запомненного угла курса и текущего программного значения, а при достижении условия А≤ε, где ε - допустимая погрешность восстановления курсовой ориентации, отключают программное управление и продолжают стабилизировать КА по сигналам ОГК.

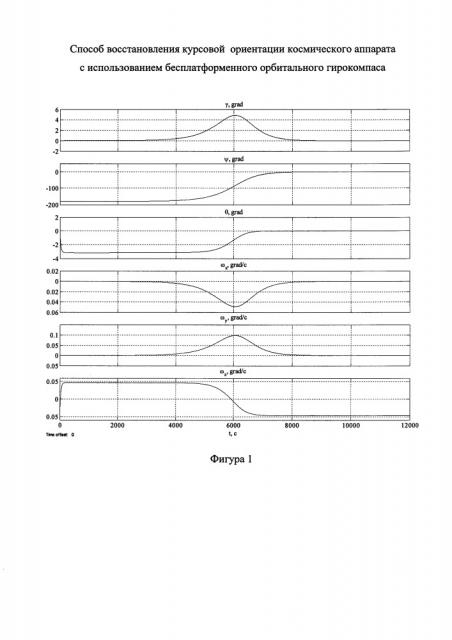
На фигурах 1 и 2 приведены результаты моделирования режима восстановления курсовой ориентации КА известным (фиг. 1) и предложенным (фиг. 2) способами.

На фигурах обозначено:

γ_grad, ψ_grad, θ_grad - угловое положение КА относительно ОСК по крену, курсу и тангажу соответственно;

- абсолютные угловые скорости КА в проекциях на собственные оси крена, курса и тангажа.

Из представленных результатов моделирования наглядно видно, что при использовании известного способа перерегулирование в каналах ориентации достигает пяти градусов, качество переходных процессов неудовлетворительное, а время восстановления курсовой ориентации КА из начального положения 180° составляет 9000 с или 2,5 часа (фиг. 1).

При использовании нового способа уравнения, описывающие процесс восстановления ориентации после выполнения условий ⎜γ_ПОЗ⎜≤Δγ, ⎜ϑ_ПОЗ⎜≤Δϑ, принимают вид [2]:

где Δβ, , Δα, , Δθ, - выходные сигналы ОГК в систему стабилизации КА по углам и угловым скоростям в каналах крена, курса и тангажа;

- аргумент разности начального запомненного угла курса и текущего программного значения λ(τ);

ω_X, ω_Y, ω_Z - угловые скорости КА относительно инерциальной системы координат (ИСК) в проекциях на связанные оси КА по крену, курсу и тангажу, измеряемые датчиками ГИУС;

γ_ПОЗ, ϑ_ПОЗ - выходные сигналы прибора ориентации по Земле (ПОЗ) по крену и тангажу;

Ω - орбитальная угловая скорость КА;

κ₁, κ₂, κ₃ - коэффициенты коррекции.

Результаты моделирования процесса восстановления курсовой ориентации КА из положения и при нулевых начальных положениях КА по γ и θ показаны на фигуре 2.

В процессе моделирования допустимая угловая погрешность ε - восстановления курсовой ориентации принималась равной 1% от полного значения , а текущее значение программной уставки λ(τ) рассчитывалось по формуле:

,

где ω_З – скорость обнуляющего программного поворота задается как максимальная допустимая угловая скорость КА в канале курса. При этом время программного поворота рассчитывалось по формуле: .

Для ω_З=0,2% и время программного поворота составило 900 с, при этом величина перерегулирования ε в канале курса не превысила 1° или 0,6%. Отклонения КА в каналах крена и тангажа относительно ОСК в течение всего времени поворота изменялись незначительно, оставаясь около нулевых значений.

Из представленных графиков видно, что заявленный технический результат достигнут как по качеству переходного процесса - процесс близок к оптимальному, так и по его времени - время переходного процесса на восстановления курсовой ориентации КА уменьшилось в ~ 10 раз или на порядок.

Источники информации

1. Бесекерский В.А., Иванов В.А., Самотокин Б.Б. Орбитальное гирокомпасирование. СПб. 251 с. 1993.

2. Патент 2509690 RU.

3. Кэмпбел, Коффи «Цифровые системы отсчета углов». Журнал «Вопросы ракетной техники», 1971 г., №11.

4. Брайсон А.Е., Кортюм В. Вычисление местного углового положения орбитального космического аппарата. Труды III Международного симпозиума ИФАК. Франция, Тулуза, 1970. Управление в космосе. Том 2. М. Наука. 23 с. 1972.

5. Раушенбах Б.В., Токарь Е.Н. Управление ориентацией космических аппаратов. М. Наука. 598 с. 1974.

6. Bowers J.L., Rodden J.J., Scott E.D., Debra D.B. Orbital Gyrocompassing Heading Reference, AIAA Journal of Spacecrat and Rockets, 1968, v.5, №8.

Способ восстановления курсовой ориентации космического аппарата (КА) с использованием бесплатформенного орбитального гирокомпаса (ОГК) относительно орбитальной системы координат (ОСК), включающий приведение КА к местной вертикали по сигналам прибора ориентации по Земле (ПОЗ) и стабилизацию КА относительно ОСК по крену и тангажу по сигналам ПОЗ и гироскопических измерителей угловой скорости (ГИУС) крена и тангажа, а также стабилизацию КА в канале курса по сигналу курсового ГИУС, отличающийся тем, что приводят КА к местной вертикали до выполнения условий

где γ _ПОЗ, ϑ _ПОЗ - сигналы ПОЗ по крену и тангажу соответственно, Δγ, Δϑ - заданные погрешности ориентации КА относительно местной вертикали, снимают показания ГИУС об угловых скоростях КА по крену и тангажу и рассчитывают положение КА по курсу относительно ОСК на момент времени t_i, например, по формуле

где ω_Xi, ω_Zi - абсолютные угловые скорость КА в каналах крена и тангажа соответственно, которое запоминают, подключают ПОЗ в контур коррекции ОГК и переходят на стабилизацию КА по сигналам ОГК с одновременным поворотом КА в плоскость орбиты со скоростью где λ(τ), τ - текущие значения программного угла, программной скорости и времени программного поворота по курсу соответственно, в процессе которого компенсируют взаимовлияние каналов ориентации перекрестными связями по аргументу разности начального запомненного угла курса и текущего программного значения, а при достижении условия А ≤ ε, где ε - допустимая погрешность восстановления курсовой ориентации, отключают программное управление и продолжают стабилизировать КА по сигналам ОГК.