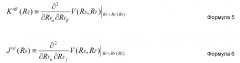Устройство имитационного моделирования для прогнозирования поведения системы точечных масс

Устройство имитационного моделирования для прогнозирования поведения системы точечных масс

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ТЕХНИКИ

Настоящее изобретение относится к устройству имитационного моделирования и способу имитационного моделирования для прогнозирования динамического поведения моделируемой системы точечных масс с использованием компьютера. Изобретение также относится к программе и носителю записи для реализации способа.

УРОВЕНЬ ТЕХНИКИ

С развитием компьютерной технологии были проведены интенсивные исследования с целью логического пояснения поведения биологических макромолекул при большой динамической деформации, например, белков, нуклеиновых кислот, липидов и полисахаридов на атомном уровне посредством имитационных моделирований с использованием теоретических вычислений. В частности, такие исследования могут включать в себя лекарственный скрининг, в котором теоретически прогнозируется сродство между целевым белком и молекулой-кандидатом на связывание (целевой молекулой для анализа наличия сродства связывания с целевым белком) и анализ механизма укладки белка, в котором выявляется механизм построения трехмерной структуры из первичной последовательности белка для теоретического построения структуры более высокой размерности из первичной структуры.

Способы имитационного моделирования для прогнозирования динамического поведения биологических макромолекул могут включать в себя, например, метод молекулярной динамики, способный к осуществлению имитационного моделирования даже для макромолекулы на атомном уровне, и способы имитационного моделирования на основе метода Монте-Карло, как описано, например, в следующих непатентных документах: T.J.A. Ewing and I.D. Kuntz, “Critical evaluation of search algorithms for automated molecular docking and database screening”, Journal of Computational Chemistry, Vol. 18, Issue 9, pp. 1175-1189, 1997, G.M. Morris et al., “Automated docking using a Lamarckian genetic algorithm and an empirical binding free energy function”, Journal of Computational Chemistry, Vol. 19, Issue 14, pp. 1639-1662, 1998, M. Rarey et al., “A Fast Flexible Docking Method using an Incremental Construction”, Journal of Molecular Biology, Vol. 261, Issue 3, pp. 470-489, 1996, R. Abagyan et al., “ICM - A new method for protein modeling and design: Applications to docking and structure prediction from the distorted native conformation”, Journal of Computational Chemistry, Vol. 15, Issue 5, pp. 488-506, 1994, G. Jones et al., “Development and validation of a genetic algorithm for flexible docking”, Journal of Molecular Biology, Vol. 267, Issue 3, pp. 727-748, 1997, R.A. Friesner et al., “Glide: A New Approach for Rapid, Accurate Docking and Scoring. 1. Method and Assessment of Docking Accuracy”, Journal of Medicinal Chemistry, Vol. 47, Issue 7, pp. 1739-1749, 2004, T.A. Halgren et al., “Glide: A New Approach for Rapid, Accurate Docking and Scoring. 2. Enrichment Factors in Database Screening”, Journal of Medicinal Chemistry, Vol. 47, Issue 7, pp. 1750-1759, 2004. Согласно методу молекулярной динамики, временная эволюция многоатомной системы можно последовательно прослеживать с малым интервалом времени согласно уравнению движения. Поскольку на потенциальной поверхности многоатомной системы, которая включает в себя биологическую макромолекулу присутствует много локальных минимумов или много энергетических барьеров, вышеупомянутый способ сталкивается с проблемой в том, что состояние многоатомной системы захватывается локальным минимумом вблизи начальной структуры, в связи с чем, для вычисления требуется большое количество времени. Эта проблема также свойственна способам на основе метода Монте-Карло.

РАСКРЫТИЕ ИЗОБРЕТЕНИЯ

Следовательно, в качестве способа решения проблемы захватывания локальным минимумом, известен способ вычисления, в котором “движущая сила” применяется к вычислению на основе метода молекулярной динамики, чтобы вырваться из ловушки локального минимума. Например, в опубликованной японской патентной заявке, не прошедшей экспертизы, № 2005-267592 и опубликованной японской патентной заявке PCT № 2005-524129, повторно опубликованной японской патентной заявке PCT № 2006/068271, и непатентных документах, Y. Fukunishi et al., “The Filling Potential Method: A Method for Estimating the Free Energy Surface for Protein-Ligand Docking”, THE JOURNAL OF PHYSICAL CHEMISTRY B, Vol. 107, Issue 47, pp. 13201-13210, 2003,and Y. Sugita and Y. Okamoto, “Replica-exchange molecular dynamics method for protein folding”, Chemical Physics Letters, Vol. 314, Issues 1-2, pp. 141-151, 1999, раскрыто, что виртуальные взаимодействия вступают последовательно, поэтому многоатомная система никогда не возвращается к прежней структуре, или структуры, найденные в ускоренном движении многоатомной системы в высокотемпературной фазе, последовательно отражаются в движении многоатомной системы в низкотемпературной фазе. Такое вступление взаимных взаимодействий и пр. может ускорять поиск маршрута на потенциальной поверхности, через которую проходит многоатомная система, что позволяет вычислять динамическое поведение биологической макромолекулы.

Однако вычисление на основании уравнения движения, описывающего систему точечных масс, представляющую моделируемую биологическую макромолекулу и т.п., и с использованием молекулярной динамики для прогнозирования поведения системы точечных масс путем интегрирования по времени, сталкивается с необходимостью поиска компромиссного соотношения между временем вычисления имитационного моделирования и точностью вычисления. В частности, в способах имитационного моделирования, описанных в опубликованной японской патентной заявке, не прошедшей экспертизы, № 2005-267592 и опубликованной японской патентной заявке PCT № 2005-524129, повторно опубликованной японской патентной заявке PCT № 2006/068271, и непатентных документах, Y. Fukunishi et al., “The Filling Potential Method: A Method for Estimating the Free Energy Surface for Protein-Ligand Docking”, THE JOURNAL OF PHYSICAL CHEMISTRY B, Vol. 107, Issue 47, pp. 13201-13210, 2003 and Y. Sugita and Y. Okamoto, “Replica-exchange molecular dynamics method for protein folding”, Chemical Physics Letters, Vol. 314, Issues 1-2, pp. 141-151, 1999, порядок движения, присущий системе точечных масс, нарушается за счет применения “движущей силы”, благодаря чему в результате вычисления вычисляется поведение нереалистично большой деформации, хотя время вычисления сокращается. Эта тенденция усиливается с увеличением “движущей силы”, прилагаемой, чтобы более эффективно вырваться из ловушки локального минимума.

Настоящее изобретение было сделано ввиду вышеописанных обстоятельств, и задачей настоящего изобретения является обеспечение устройства имитационного моделирования и способа имитационного моделирования, позволяющих повысить точность вычисления и одновременно сократить время вычисления в имитационного моделирования для прогнозирования динамического поведения системы точечных масс. Еще одной задачей настоящего изобретения является обеспечение программы и носителя записи для реализации способа.

Для решения вышеупомянутых проблем, устройством имитационного моделирования согласно настоящему изобретению является устройство для прогнозирования поведения системы точечных масс, образованной моделируемыми N точечными массами, причем устройство включает в себя:

средство задания координат для задания медленных координат, которые представляют собой M координат, в основном предполагающих структурное изменение в системе точечных масс на основании 3N координат точечных масс, описывающих структуру системы точечных масс, и быстрых координат, которые являются координатами, описывающими структуру системы точечных масс, и не зависят от медленных координат;

средство извлечения координат для получения структуры быстрых координат как функции медленных координат путем подчинения быстрых координат медленным координатам и получения, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, структуры медленных координат как функции K коллективных координат общей координаты, которая связана с медленными координатами каноническим преобразованием, причем общая координата образована переменной составляющей, которая изменяется со временем, и постоянной составляющей, которая служит константой относительно времени, и K коллективных координат являются переменной составляющей общей координаты; и

средство обратного преобразования для прогнозирования временной эволюции системы точечных масс на основании коллективной(ых) координаты() как функции времени, которую(ые) можно получить, решая уравнение движения относительно коллективной(ых) координаты(), структуры медленных координат и структуры быстрых координат.

K, M, и N здесь удовлетворяют соотношению K<M<3N, и каждое из них представляет целое число, не меньшее 1.

Используемый здесь термин “структура системы точечных масс” означает трехмерную структуру, образованную N точечными массами, составляющими систему точечных масс.

Используемый здесь термин “медленные координаты, в основном, предполагающие структурное изменение в системе точечных масс” означает координаты, которые оказывают большое влияние на формирование трехмерной структуры системы точечных масс.

Используемый здесь термин “задание медленных координат” означает задание, в качестве медленных координат, некоторых из координат самих точечных масс, координат, которые можно задавать путем объединения координат точечных масс, или их комбинации. То же самое справедливо для быстрых координат.

Предпочтительно, средство извлечения координат устройства имитационного моделирования согласно настоящему изобретению является средством, которое получает структуру медленных координат путем:

осуществления первого этапа для получения потенциальной энергии V, представленной как функция медленных координат и быстрых координат;

осуществления второго этапа для подчинения быстрых координат медленным координатам согласно условию адиабатического приближения с использованием потенциальной энергии;

осуществления, в текущем состоянии медленных координат и быстрых координат, третьего этапа для получения производной потенциальной энергии по медленным координатам с учетом влияния вышеописанный;

осуществления, на основании производной потенциальной энергии, четвертого этапа для получения производной медленных координат по коллективной(ым) координате(ам) согласно основному уравнению метода самосогласованных коллективных координат с использованием производной потенциальной энергии;

осуществления, на основании производной медленных координат, пятого этапа для обновления коллективной(ых) координаты() на малую величину и получения обновленных медленных координат;

осуществления, на основании обновленных медленных координат, шестого этапа для осуществления структурной релаксации на быстрых координатах, подчиненных медленным координатам; и

после этого повторения этапов с третьего по шестой на основании медленных координат и быстрых координат в состоянии после структурной релаксации быстрых координат.

Используемый здесь термин “на основании медленных координат и быстрых координат в текущем состоянии” означает, что третий этап осуществляется, когда медленные координаты и быстрые координаты находятся в состоянии, заданном средством задания координат в первый момент времени, и когда медленные координаты и быстрые координаты находятся в состоянии после структурной релаксации, осуществляемой на быстрых координатах во второй момент времени непосредственно до осуществления шестого этапа.

Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, вышеописанное влияние учитывается способом, который использует, по меньшей мере, одну из нижеприведенных формул 1-3.

Используемое здесь далее означает следующее:

каждое из i, j и k представляет целое число в диапазоне от 1 до M;

каждое из α, β и γ представляет целое число в диапазоне от 1 до 3N-M;

R_Si представляет i-ю медленную координату в системе точечных масс;

R_Fα представляет α-ю быструю координату в системе точечных масс;

R_S представляет (R_S1, R_S2, ------, R_SM);

R_F представляет (R_F1, R_F2, ------, R_F(3N-M));

R_F(R_S) представляет быстрые координаты, подчиненные медленным координатам;

V(R_S,R_F) представляет потенциальную энергию системы точечных масс, представленной медленными координатами и быстрыми координатами; и

V_eff(R_S) представляет эффективную потенциальную энергию, получаемую подстановкой R_F(R_S) в V(R_S,R_F).

В формуле 2, (i↔j) в третьем члене представляет член, выведенный взаимной заменой индексов i и j во втором члене (то есть члене, выведенном путем замены i на j и j на i во втором члене, то же самое справедливо ниже).

В формуле 3, (i↔k) в третьем члене представляет член, выведенный взаимной заменой индексов i и k во втором члене, (j↔k) в четвертом члене представляет член, выведенный взаимной заменой индексов j и k во втором члене, (i↔k) в шестом члене представляет член, выведенный взаимной заменой индексов i и k в пятом члене, и (j↔k) в седьмом члене представляет член, выведенный взаимной заменой индексов j и k в пятом члене.

Кроме того, в формулах 1-3, используется нижеприведенная формула 4.

где: K_αβ^-1(R_S) представляет матрицу, обратную K^αβ(R_S), и

K^αβ(R_S) и J^αi(R_S) задаются нижеприведенными формулами 5 и 6, соответственно.

Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, условие адиабатического приближения выражается нижеприведенной формулой 7.

Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, количество K коллективных координат удовлетворяет условию K=1, и основное уравнение метода самосогласованных коллективных координат представлено нижеприведенными формулами 8 и 9.

Используемое здесь далее означает следующее:

q¹ представляет коллективную координату;

m_i представляет массу i-й медленной координаты в системе точечных масс;

ϕ_i(R_S) представляет i-ю составляющую функции (собственный вектор), которая удовлетворяет формуле 9; и

Λ(R_S) представляет функцию (собственное значение), которая удовлетворяет формуле 9.

Альтернативно, предпочтительно, чтобы в устройстве имитационного моделирования настоящего изобретения количество K коллективных координат удовлетворяло условию K=1, и основное уравнение метода самосогласованных коллективных координат было представлено нижеприведенными формулами 10-12.

где ϕ_i(R_S, λ) и κ(R_S, λ) - функции, которые подчиняются формуле 12, и ϕ_i(R_S, λ) представляет i-ю составляющую, и λ представляет вспомогательную координату (переменную, рассматриваемую как независимую от медленных координат и как функцию коллективной(ых) координаты()).

Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, средство извлечения координат является средством, которое осуществляет вычисление на четвертом этапе путем увеличения количества переменных, рассматриваемых как независимые от медленных координат и как функции коллективной(ых) координаты() (т.е. вспомогательных координат) при решении основного уравнения для исключения произвольности знака производной медленных координат или вспомогательных координат относительно коллективной(ых) координаты() в основном уравнении.

Кроме того, в случае, когда количество вспомогательных координат увеличивается, предпочтительно, чтобы средство извлечения координат являлось средством, которое осуществляет вычисление согласно основному уравнению, представленному нижеприведенной формулой 13, полученной в результате этого. Кроме того, в этом случае, количество K коллективных координат удовлетворяет условию K=1.

где Y - MK+M+K-мерный вектор, заданный нижеприведенной формулой 14, и v^μ - вектор решения неоднородного линейного уравнения нижеприведенной формулы 15.

C и s^μ в формуле 15 задаются нижеприведенными формулами 16 и 17, соответственно.

где V_ij(R_S) и V_ijk(R_S) задаются нижеприведенными формулами 18 и 19, соответственно.

где каждое из μ и ν представляет целое число в диапазоне от 1 до K, q^μ представляет μ-ю коллективную координату, и каждое из ϕ_i^μ и Λ^μ представляет вспомогательную координату.

Альтернативно, в случае, когда количество вспомогательных координат увеличивается, предпочтительно, чтобы средство извлечения координат являлось средством, которое осуществляет вычисление согласно основному уравнению, представленному нижеприведенной формулой 20, полученной в результате этого. Кроме того, в этом случае, количество K коллективных координат удовлетворяет условию K=1.

где Z - MK+M+2K-мерный вектор, заданный нижеприведенной формулой 21, c^μν - константа, уникально определенная так, чтобы минимизировать значение, представленное нижеприведенной формулой 22, задаваемое относительно каждого μ, и w^μ представляет один из K MK+M+2K-мерных единичных векторов, образующих базис K-мерного пространства сингулярных значений матрицы D, заданной нижеприведенной формулой 23. Заметим, что каждое из λ^μ и ρ^μ представляет вспомогательную координату, независимую от R_S, наподобие ϕ_i^μ.

Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, средство извлечения координат является средством, которое вычисляет член третьей производной потенциальной энергии на основании нижеприведенной формулы 24. ϕ_i представляет i-ю составляющую произвольного вектора, и n задается нижеприведенной формулой 25.

Предпочтительно, в устройстве имитационного моделирования настоящего изобретения, средство задания координат является средством, которое задает репрезентативные координаты, извлеченные из и представляющие каждую характеристическую частичную структуру структуры системы точечных масс в качестве медленных координат.

Используемый здесь термин “характеристическая частичная структура” означает частичную структуру структуры системы точечных масс, имеющую морфологические и/или функциональные характеристики.

В устройстве имитационного моделирования настоящего изобретения, система точечных масс может представлять собой многоатомную систему, который включает в себя биологическую макромолекулу, частичная структура может представлять собой вторичную структуру, строительный блок или основную цепь биологической макромолекулы, и репрезентативная координата каждой частичной структуры является координатой каждого из атомов, составляющих частичную структуру, координатой, заданной путем объединения координат атомов, или шагом частичных структур.

В устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была белком, частичная структура была вторичной структурой белка, и репрезентативная координата вторичной структуры была координатой центра тяжести группы атомов, составляющей вторичную структуру, или углом сгиба вторичной структуры. В этом случае, предпочтительно, чтобы вторичная структура была, по меньшей мере, одной из спиральной структуры, β-листа, витка, петли и случайной спирали.

Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была белком, частичная структура была остатком белка, и репрезентативная координата остатка была координатой центра тяжести группы атомов, составляющих остаток.

Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была белком, частичная структура была основной цепью белка, и репрезентативная координата основной цепи была координатой каждого атома составляющего основную цепь.

Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была нуклеиновой кислотой, частичная структура была вторичной структурой нуклеиновой кислоты, и репрезентативная координата вторичной структуры была координатой центра тяжести группы атомов, составляющей вторичную структуру, или углом сгиба вторичной структуры. В этом случае, предпочтительно, чтобы вторичная структура была спиральной структурой.

Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была нуклеиновой кислотой, частичная структура была остатком нуклеиновой кислоты, и репрезентативная координата остатка была координатой центра тяжести группы атомов, составляющих остаток.

Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была нуклеиновой кислотой, частичная структура была основной цепью нуклеиновой кислоты, и репрезентативная координата основной цепи была координатой каждого атома составляющего основную цепь.

Кроме того, в устройстве имитационного моделирования настоящего изобретения, если система точечных масс является многоатомной системой, которая включает в себя биологическую макромолекулу, предпочтительно, чтобы биологическая макромолекула была нуклеиновой кислотой, частичная структура была спиральной структурой нуклеиновой кислоты, и репрезентативная координата спиральной структуры была шагом спиральной структуры.

Кроме того, в устройстве имитационного моделирования настоящего изобретения, многоатомная система может включать в себя молекулу-кандидат на связывание для биологической макромолекулы.

Способ имитационного моделирования настоящего изобретения представляет собой способ, используемый с вышеописанным устройством имитационного моделирования для прогнозирования поведения системы точечных масс, образованной моделируемыми N точечными массами, причем способ включает в себя этапы, на которых:

задают медленные координаты, которые представляют собой M координат, в основном, предполагающих структурное изменение в системе точечных масс на основании 3N координат точечных масс, описывающих структуру системы точечных масс;

задают быстрые координаты, которые являются координатами, описывающими структуру системы точечных масс, и не зависят от медленных координат;

получают структуру быстрых координат как функции медленных координат путем подчинения быстрых координат медленным координатам;

получают, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, структуру медленных координат как функции K коллективных координат общей координаты, которая связана с медленными координатами каноническим преобразованием, причем общая координата образована переменной составляющей, которая изменяется со временем, и постоянной составляющей, которая служит константой относительно времени, и K коллективных координат являются переменной составляющей общей координаты; и

прогнозируют временную эволюцию системы точечных масс на основании коллективной(ых) координаты() как функции времени, которую(ые) можно получить, решая уравнение движения относительно коллективной(ых) координаты(), структуры медленных координат и структуры быстрых координат.

Программа имитационного моделирования настоящего изобретения представляет собой программу, которая предписывает компьютеру осуществлять вышеописанный способ имитационного моделирования.

Компьютерно-считываемый носитель записи настоящего изобретения представляет собой носитель, на котором записана вышеописанная программа имитационного моделирования.

Устройство имитационного моделирования настоящего изобретения включает в себя вышеописанные средство задания координат, средство извлечения координат и средство обратного преобразования, и прогнозирует временную эволюцию координат точечных масс, вводя иерархически упорядоченные медленные координаты, извлекая, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, коллективную координату в теории коллективного движения, которая описывает коллективное и собственное поведение системы точечных масс, и решая уравнение движения относительно коллективной координаты. Таким образом, извлечение коллективной координаты позволяет осуществлять имитационное моделирование на атомном уровне, и введение медленных координат позволяет сокращать количество координат, обрабатываемых для извлечения коллективной координаты. В результате, можно добиться, как повышения точности вычисления, так и сокращения времени вычисления при имитационного моделирования для прогнозирования динамического поведения системы точечных масс.

Способ имитационного моделирования настоящего изобретения представляет собой способ, используемый с вышеописанным устройством имитационного моделирования, и предусматривает прогнозирование временной эволюции координат точечных масс посредством ввода иерархически упорядоченных медленных координат, извлечения, с учетом влияния изменения быстрых координат на медленные координаты вследствие изменения медленных координат, коллективной координаты в теории коллективного движения, которая описывает коллективное и собственное поведение системы точечных масс, и решения уравнения движения относительно коллективной координаты. Таким образом, извлечение коллективной координаты позволяет осуществлять имитационное моделирование на атомном уровне, и введение медленных координат позволяет сокращать количество координат, обрабатываемых для извлечения коллективной координаты. В результате, можно добиться, как повышения точности вычисления, так и сокращения времени вычисления при имитационного моделирования для прогнозирования динамического поведения системы точечных масс.

Программа и носитель записи настоящего изобретения могут предписывать осуществление вышеупомянутого способа имитационного моделирования, что позволяет достигать повышенной точности вычисления и сокращенного времени вычисления в имитационного моделирования для прогнозирования динамического поведения системы точечных масс.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Фиг. 1 - схема, демонстрирующая процесс связывания белка и молекулы-кандидата на связывание в случае, когда индуцированное соответствие учитывается в способе имитационного моделирования настоящего изобретения.

Фиг. 2 - схема, демонстрирующая путь реакции на принципиальной потенциальной поверхности многоатомной системы, которая включает в себя белок и молекулу-кандидат на связывание, где учитывается индуцированное соответствие.

Фиг. 3 - вид, принципиально демонстрирующий процесс для получения пути реакции многоатомной системы с использованием извлечения коллективной координаты.

Фиг. 4 иллюстрирует принцип преобразования переменных и обратного преобразования.

Фиг. 5 - блок-схема устройства имитационного моделирования согласно варианту осуществления, схематически демонстрирующая его конфигурацию.

Фиг. 6A - блок-схема операций, схематически демонстрирующая этапы вычисления способа имитационного моделирования согласно варианту осуществления.

Фиг. 6B - блок-схема операций, схематически демонстрирующая этапы вычисления способа имитационного моделирования согласно варианту осуществления.

Фиг. 7 схематически иллюстрирует соотношение между медленными координатами R_S, быстрыми координатами R_F и атомными координатами x.

Фиг. 8 - график, демонстрирующий путь реакции заранее определенного составного тела, полученного способом имитационного моделирования согласно варианту осуществления.

Фиг. 9 - схема, демонстрирующая процесс связывания составного тела, показанного на графике на Фиг. 8, в котором A и B иллюстрируют начальное состояние и конечное состояние процесса связывания составного тела соответственно.

Фиг. 10 - график, демонстрирующий результат сравнения между вычислением, в котором произвольность знака исключается, и вычислением, в котором произвольность знака не исключается.

ПРЕДПОЧТИТЕЛЬНЫЕ ВАРИАНТЫ ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ

Вариант осуществления настоящего изобретения будет описан ниже со ссылкой на прилагаемые чертежи, но следует понимать, что настоящее изобретение не ограничивается вариантом осуществления. Заметим, что каждая деталь в чертежах не обязательно изображена в масштабе для простоты визуального распознавания.

Прежде чем перейти к подробному описанию, сначала опишем техническую идею, лежащую в основе настоящего изобретения, и предпосылки настоящего изобретения для пояснения технических преимуществ настоящего изобретения над уровнем техники. Для наглядности объяснения, конкретное описание будет приведено для случая прогнозирования динамического поведения многоатомной системы, которая включает в себя составное тело биологической макромолекулы и молекулы-кандидаты на связывание.

Прогнозирование динамического поведения многоатомной системы наподобие вышеописанной играет важную роль, например, при разработке нового лекарственного препарата с точки зрения сокращения периода и стоимости разработки. Физиологически активное вещество, например лекарственный препарат, может демонстрировать химическое свойство за счет связывания с конкретным белком. Поэтому при разработке нового лекарственного препарата необходимо сужать круг кандидатов, которые с большой вероятностью связываются с целевым белком, из большого количества соединений в пределах от нескольких сотен тысяч до нескольких миллионов (лекарственный скрининг). Кроме того, в конце концов, требуется сужать круг кандидатов в лекарственные препараты до нескольких кандидатов. Чтобы эффективно сужать круг кандидатов в лекарственные препараты от большого количества соединений, необходимо рассматривать поведение многоатомной системы на атомном уровне и точно оценивать взаимодействия между молекулами и, далее, между атомами.

На Фиг. 1 показана схема, демонстрирующая процесс связывания белка и молекулы-кандидата на связывание в случае, при рассмотрении динамического поведения белка. Белок 2 имеет карман 4 для связывания молекулы-кандидата 6 на связывание. То есть можно сказать, что молекула-кандидат 6 на связывание является физиологически активным веществом белка 2. Заметим однако, что карман 4 не обязательно имеет форму, которая позволяет молекуле-кандидату 6 на связывание непосредственно усаживаться в нем (Фиг. 1a). Например, Фиг. 1 иллюстрирует, что размер отверстия кармана 4 меньше, чем размер молекулы-кандидата 6 на связывание. Следовательно, в таком случае, белок 2 изменяет свою структуру, чтобы адаптировать форму и размер отверстия к форме и размеру молекулы-кандидата 6 на связывание согласно взаимодействию с приближающейся молекулой-кандидатом 6 на связывание (Фиг. 1b и c).

Явление, состоящее в том, что биологическая макромолекула, например, белок, нуклеиновая кислота, и т.п., изменяет свою структуру в результате взаимодействия с физиологически активным веществом вышеописанным образом, именуется “индуцированным соответствием”. Для точного вычисления взаимодействия между молекулами, естественно, следует учитывать “индуцированное соответствие”. Это можно реализовать, рассматривая многоатомную систему на атомном уровне.

На Фиг. 2 показана схема, демонстрирующая путь реакции на принципиальной потенциальной поверхности многоатомной системы, в которой учитывается индуцированное соответствие. Горизонтальная ось X₁ на Фиг. 2 принципиально иллюстрирует структурное изменение в белке, и вертикальная ось X₂ иллюстрирует расстояние между белком и молекулой-кандидатом на связывание. Таким образом, Фиг. 2 представляет потенциальную поверхность многоатомной системы согласно структурному изменению в белке и расстоянию между молекулами. Как показано на Фиг. 2, система, в которой возникает индуцированное соответствие, имеет энергетический барьер B (седловую точку) на пути RP реакции, соединяющем две стабильные точки (точку A, в которой составное тело находится в диссоциированных телах, и точку B, в которой связывание составного тела завершено).

Таким образом, анализ процесса связывания белка 2 и молекулы-кандидата 6 на связывание с учетом индуцированного соответствия сводится, в сущности, к поиску пути реакции, соединяющего две стабильные точки A и C, через энергетический барьер B на потенциальной поверхности по отношению к белку 2 и молекуле-кандидату 6 на связывание.

Ввиду вышеизложенного, для достижения повышенной точности вычисления и сокращенного времени вычисления в имитационного моделирования для прогнозирования динамического поведения многоатомной системы, необходимо иметь возможность рассматривать многоатомную систему на атомном уровне и облегчать поиск неэмпирического пути реакции.

Однако поведение многоатомной системы, содержащей от нескольких тысяч до нескольких миллионов атомов, является медленным, и большая деформация, которая возникает в масштабе времени порядка от получаса до часа. В связи с этим, традиционные способы имитационного моделирования сталкиваются с проблемой, состоящей в том, что теоретическое вычисление требует большого количества времени, нескольких декад, хотя они могут рассматривать многоатомную систему на атомном уровне. Следовательно, чтобы иметь возможность осуществлять теоретическое вычисление поведения многоатомной системы в течение практически приемлемого периода времени, были изучены или разработаны различные способы имитационного моделирования. Метод молекулярной динамики, в котором прилагается “движущая сила”, является одним из таких способов имитационного моделирования, но он сталкивается с вышеупомянутой проблемой. Также исследуется другой способ, который сокращает объем вычислений за счет аппроксимации целевого белка твердым телом и уменьшения количества используемых переменных. Однако такое грубое приближение, естественно, не может учитывать влияние динамического поведения белка, что не позволяет точно вычислять взаимодействия, действующие между молекулами. В таком случае, например, один миллион соединений-кандидатов можно сузить лишь до около десяти тысяч соединений в качестве кандидатов в лекарственные препараты. Проблема компромиссного соотношения между временем вычисления и точностью вычисления сохраняется и в других способах имитационного моделирования.

Автор настоящего изобретения предложил идею моделировать многоатомную систему, которая включает в себя биологическую макромолекулу, системой точечных масс, имеющей N точечных масс, и рассматривать поведение системы точечных масс как коллективное движение, и извлекать коллективную координату, имеющую меньшую степень свободы, чем у координат точечных масс (координат точечных масс, которые одномерно описывают структуру системы точечных масс) из коллективного движения на основании координат точечных масс.

Коллективная координата

Ниже будет описана коллективная координата. В общем случае, термин “коллективная координата” означает элемент коорд