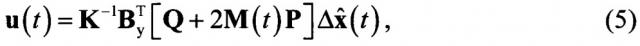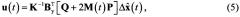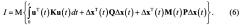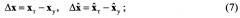Способ нелинейного управления инерционным приводом антенны, обеспечивающий высокую устойчивость сопровождения интенсивно маневрирующих объектов

Способ нелинейного управления инерционным приводом антенны, обеспечивающий высокую устойчивость сопровождения интенсивно маневрирующих объектов

Иллюстрации

Показать все

Реферат

Изобретение относится к системам автоматического сопровождения целей по угловым координатам.

Расширение номенклатуры сверхманевренных и гиперзвуковых летательных аппаратов (ЛА) приводит к усложнению взаимодействия ЛА, что проявляется в значительном усложнении законов изменения входных воздействий для БРЛС. В связи с этим, к РЛС ЛА и беспилотных летательных аппаратов (БЛА) предъявляются высокие требования к точности, быстродействию и устойчивости сопровождения целей [1]. При этом необходимо отметить, что среди всех видов информационных датчиков наибольшее влияние на точность и устойчивость наведения ЛА оказывают угломерные каналы бортовых РЛС [1, 2].

В связи с этим при оптимизации систем радиоуправления первоочередной задачей является расширение диапазонов углов и угловых скоростей устойчивого сопровождения целей угломером и улучшение его точности.

Особенностью функционирования существующих угломеров с типовой моноимпульсной пеленгацией [2] является ограничение допустимых ошибок Δϕ захвата и сопровождения величиной, соответствующей половине ширины θ диаграммы направленности антенны.

Причиной этого является специфика пеленгационной характеристики угломера, которая предопределяет изменение знака сигналов отрицательной обратной связи на положительную при выполнении условия |Δϕ|>θ/2, что автоматически приводит к срыву сопровождения.

Эта особенность предопределяет необходимость формирования требуемых сигналов управления

только при выполнении условия

Достоинством классического метода управления (1) является его простота. Недостаток - одинаковая чувствительность (скорость изменения сигналов управления) как к большим, так и малым ошибкам сопровождения. В то же время желательно иметь вблизи границы устойчивой работы угломера (Δϕ≈θ/2) значительно большую скорость нарастания сигнала управления, обеспечивающую ускоренную ликвидацию опасных ошибок сопровождения, уменьшая тем самым риск срыва сопровождения.

Задачей изобретения является разработка способа управления угломером, обеспечивающего высокую устойчивость сопровождения интенсивно маневрирующих целей.

Поставленная задача достигается тем, что сигнал управления, определяемый взвешенной суммой ошибок функционирования, дополняется слагаемыми, имеющими квадратичную и кубическую зависимости от ошибок сопровождения, что позволит обеспечить высокую скорость нарастания сигнала управления вблизи границы устойчивой работы угломера.

Технический результат, который может быть получен от использования предлагаемого изобретения, заключается в повышении устойчивости и точности сопровождения маневрирующих целей, за счет адаптивной чувствительности сигналов управления к ошибкам сопровождения.

Сущность предлагаемого изобретения заключается в том, что в системе измеряют фазовые координаты состояния входящих в систему подсистем в процессе их совместного функционирования и формируют сигнал управления в виде взвешенной суммы линейных и нелинейных комбинаций оценок ошибок сопровождения.

Задача будет решаться на основе математического аппарата статистической теории управления [3] с использованием аппарата локальной оптимизации [4], который позволяет для системы

предназначенной для отработки процесса

сформировать сигнал управления

оптимальный по минимуму квадратично-биквадратного функционала качестве

Здесь х_т и х_у - n-мерные векторы требуемых и управляемых координат;

F_т и F_y - матрицы внутренних связей векторов (3) и (4);

В_у - матрица эффективности r-мерного (r≤n) вектора и сигналов управления;

ξ_т и ξ_у - векторы центрированных гауссовских возмущений состояния;

и - векторы оптимальных оценок процессов (4) и (3);

Q - матрица штрафов за точность приближения х_у к х_т;

Р - матрица взаимовлияния линейной и кубичной составляющих управления (5);

t - текущее время.

В ходе решения задачи будет считаться, что сигналы управления в горизонтальной и вертикальной плоскостях не влияют друг на друга, в связи с чем далее будет рассмотрено формирование сигнала управления только в горизонтальной плоскости.

В математическом плане задача формулируется следующим образом.

Для типового привода антенны, определяемого моделью [1]

предназначенного для сопровождения цели, движущейся по закону [1]

необходимо сформировать сигнал управления u_ω, оптимальный по минимуму функционала качества

где

при условии, что измеряется бортовой пеленг цели

Здесь ϕ_г и ϕ_у - бортовой пеленг цели и угол поворота антенны угломера в горизонтальной плоскости;

ω_г и ω_у - угловые скорости линии визирования и поворота антенны;

b и Т - коэффициент передачи и постоянная времени привода;

ξ_г и ξ_у - центрированные гауссовские шумы состояния (9) и (10);

Д и - дальность до цели и скорость ее изменения;

ϕ_уи - измерения датчика углового положения антенны;

Δϕ_пи - измерения моноимпульсного пеленгатора.

Геометрические соотношения между всеми координатами состояния и измерениями показаны на фигуре 1, на которой

О_н и О_ц - точки расположения носителя и цели;

V_н и V_ц - векторы скорости носителя и цели;

Х_рсн - положение равносигнального направления в пространстве.

Необходимо отметить адекватность модели (10) широкому полю условий применения, так как манипулируя законами изменения j_г, можно реализовать изменения угловых координат практически любой сложности.

Поскольку исходные модели (9), (10) и (13) линейные, функционал (11) представляет разновидность квадратичного, а возмущения гауссовские (ЛКГ-задача) [5], то на основании теоремы разделения задача управления может решаться в детерминированной постановке, независимо от задачи фильтрации, при условии, что в полученном результате координаты состояния будут заменены их оптимальными оценками.

Поставив в соответствие (9) - (11) с (3) - (8), получим

Тогда, используя (14) в (5), будем иметь:

где в соответствии с выводами теоремы разделения

Анализ (15), (16) позволяет сделать следующие выводы.

Следящий угломер представляет многоконтурную систему с обратными связями по углу и угловой скорости.

В состав сигнала управления входят линейная составляющая, определяемая первыми двумя слагаемыми, и нелинейная составляющая в виде третьего, четвертого и пятого слагаемых.

Сигнал управления зависит не только от ошибок Δϕ и Δω, но и от их соотношений и сочетаний Δϕ²Δω и ΔϕΔω².

Сигнал управления зависит не от абсолютных значений коэффициентов штрафов, а от их соотношений q₂₁/k_ω, q₂₂/k_ω и p₂₁/k_ω, p₂₂/k_ω. При этом степень влияния нелинейных слагаемых на величину сигнала управления определяются значениями коэффициентов матрицы Р.

Для получения сигнала управления достаточно иметь оценки бортового пеленга, угловой скорости линии визирования и угла поворота антенны и скорости его изменения, что не накладывает ограничений на возможность его реализации.

Полагая в (15) матрицы М и Р диагональными, можно получить более простые варианты сигналов управления.

Исследование полученного алгоритма проводилось по результатам имитационного моделирования сложных пространственных эволюций интенсивно маневрирующей цели, содержащих высокие производные угловых координат, определяемых законами изменения угла и угловой скорости:

с устранением первоначальных ошибок захвата различного сочетания

Следует отметить, что исследования проводились для наиболее жестких условий, когда законы (17) и (18) не соответствуют модели (10), положенной в основу синтеза закона управления. Достоинством (17) и (18) является то, что манипулируя ϕ_ц(θ), , , , , А, с₁, можно получить законы изменения ϕ_ц практически любой сложности. Наряду с моделированием (10), моделировался привод (9) и алгоритм управления (15).

В ходе моделирования полученный закон сравнивался с используемым на практике прототипом, в котором используются только компоненты, линейно зависящие от ошибок по углу и угловой скорости:

Эффективность сравниваемых законов управления оценивалась по величинам текущих ошибок сопровождения и времени регулирования.

Исследования проводились в несколько этапов.

На первом этапе исследовалась способность управления (15) функционировать при различных постоянных времени привода, результаты моделирования приведены на фигурах 2 и 3. При этом на фигуре 2 показана зависимость относительных текущих ошибок по углу и угловой скорости для вариантов а) Т=1с; б) Т=2с; в) Т=3с; г) Т=4с; д) Т=5с. На фигуре 3 приведена зависимость времени регулирования от постоянной времени угломера. Из рисунков следует, что исследуемый угломер способен ликвидировать ошибки захвата даже при очень большой инерционности привода. Однако при этом значительно увеличиваются текущие ошибки как по углу (фигура 2а), так и по угловой скорости (фигура 2б).

На втором этапе исследовались показатели точности и быстродействия при сложном (17) законе изменения угловых координат. На фигурах 4а, б и 5а, б показаны зависимости относительных текущих ошибок сопровождения от времени при движении цели по закону (17) с использованием законов управления (15) (фигура 4а, б) и (20) (фигура 5а, б) при различных вариантах первоначальных ошибок захвата (19).

На третьем этапе исследовалась эффективность угломера при самом сложном для сопровождения законе (змейке) (18) со сменой знаков производных. Показатели текущих относительных ошибок сопровождения цели, выполняющей маневр «змейка», приведены на фигурах 6а, б (для алгоритма (15)) и 7а, б (для алгоритма (20)). Следует отметить, что при использовании алгоритма (20) ошибки сопровождения неограниченно возрастают, что приводит к срыву сопровождения, в то время как при использовании алгоритма (15) обеспечиваются более высокие показатели устойчивости и точности по сравнению с законом (20).

По результатам моделирования можно сделать следующие выводы:

- предложенный алгоритм нелинейного управления угломером позволяет обеспечить бессрывное высокоточное сопровождение целей, движущихся по очень сложным законам, в том числе и со сменой знаков производных;

- система устойчиво отрабатывает начальные ошибки захвата любых знаков при любом их сочетании, даже при достаточно большой постоянной времени привода угломера.

- манипулируя в (15) коэффициентами матриц М и Р, можно получить широкий спектр разновидностей нелинейного управления.

Упрощенная структура системы, реализующей предложенный способ, показана на фигуре 8, где

1 - антенна, формирующая наблюдения z и передающая их на фильтр 2;

2 - фильтр, принимающий на вход наблюдения антенны 1, формирующий оценки , , , и передающий их на усилители 3-7;

3 - усилитель, получающий оценки , , формирующий сигнал - и передающий его на сумматор 8;

4 - усилитель, получающий оценки , , формирующий сигнал - и передающий его на сумматор 8;

5 - усилитель, получающий оценки , , , , формирующий сигнал и передающий его на сумматор 8;

6 - усилитель, получающий оценки , , , , формирующий сигнал и передающий его на сумматор 8;

7 - усилитель, получающий оценки , , формирующий сигнал и передающий его на сумматор 8;

8 - сумматор, получающий на вход сигналы из усилителей 3-7, формирующий сигнал управления u_a и передающий его на привод антенны 9;

9 - привод антенны, получающий на вход сигнал управления u_a и формирующий положение антенны 1.

Функциональное назначение представленной на фигуре 8 структурной схемы управления заключается в формировании сигнала в виде взвешенной суммы оценок и фазовых координат системы и их нелинейных комбинаций , и .

Использование изобретения позволит осуществлять бессрывное высокоточное сопровождение целей, движущихся по очень сложным законам, в том числе и со сменой знаков производных. Также следует отметить, что информационное обеспечение предлагаемого алгоритма управления может быть осуществлено в существующих системах с учетом реальных ограничений, что свидетельствует о возможности практической реализации метода.

Список использованных источников

1. Меркулов В.И., Дрогалин В.В., Канащенков А.И. и др. Авиационные системы радиоуправления. Т. 2. Радиоэлектронные системы самонаведения. /Под ред. А.И. Канащенкова и В.И. Меркулова - М.: Радиотехника, 2003.

2. Леонов А.И., Фомичев К.И. Моноимпульсная радиолокация. - М.: Радио и связь, 1984.

3. Сейдж Э., Уайт Ш Ч.С. Оптимальное управление системами. / Пер. с англ. - М.: Радио и связь, 1982.

4. Меркулов В.И. Оптимизация систем управления по локальным квадратично-биквадратным функционалам качества. //Информационно-измерительные и управляющие системы. 2016. №11. С. 27-33.

5. Черноусько Ф.А., Колмановский В.Б. Оптимальное управление при случайных возмущениях. - М.: Наука, 1978.

Способ нелинейного управления инерционным приводом антенны угломера, заключающийся в том, что формируют оптимальные оценки бортового пеленга цели , угла поворота антенны , угловой скорости линии визирования , угловой скорости поворота антенны , на основе которых по закону

формируют сигнал управления приводом угломера, где

b - коэффициент передачи,

T - постоянная времени угломера,

k_ω - коэффициент усиления привода угломера,

q₂₁ и q₂₂ - коэффициенты штрафов за ошибки сопровождения по углу и угловой скорости,

р₁₁, р₂₁ и р₂₂ - коэффициенты взаимовлияния линейной и кубичной составляющих управления,

и затем передают его потребителю.