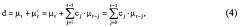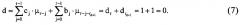Способ раскрытия структуры нелинейных рекуррентных последовательностей в виде кодов квадратичных вычетов, существующих в простых полях галуа gf(p), и устройство для его реализации

Способ раскрытия структуры нелинейных рекуррентных последовательностей в виде кодов квадратичных вычетов, существующих в простых полях галуа gf(p), и устройство для его реализации

Иллюстрации

Показать все

Реферат

1. Область применения, к которой относится изобретение

Изобретение относится к способам и устройствам обработки данных в широкополосной радиосвязи и радионавигации, где этапу приема информационных сигналов с расширенным спектром, манипулированных некоторой псевдослучайной последовательностью (ПСП), обязательно предшествуют этапы поиска и синхронизации, а также к вычислительной технике, использующейся в системах связи со сложными сигналами (шумоподобными сигналами - ШПС).

Как известно, в качестве расширяющих спектр сигнала функций для создания ШПС используют различного вида ПСП, структурные свойства которых определяют значения показателей помехозащищенности (помехоустойчивости от естественных и преднамеренных помех, скрытности и имитостойкости) использующих их систем. Прежде всего, для данных целей применяются линейные рекуррентные последовательности (ЛРП), и, в частности, М-последовательности (последовательности максимального периода).

М-последовательности очень просто генерируются посредством регистра, сдвига с линейными обратными связями (РСЛОС), что в совокупности с хорошими корреляционными и спектральными свойствами обосновывает их широкое применение в системах связи со сложными сигналами (Варакин Л.Е. Системы связи с шумоподобными сигналами - М.: Радио и связь, 1985. - 384 с.).

Однако использование М-последовательностей в системах, к которым предъявляются повышенные требования по скрытности и имитостойкости, является нецелесообразным, ввиду того, что последние имеют ряд существенных недостатков, а именно, М-последовательности:

существуют для ограниченного числа длительностей L=2ⁿ-1, где n=2, 3, …;

имеют небольшую мощность кодирования. Так, согласно (Свердлик М.Б. Оптимальные дискретные сигналы. М.: изд-во «Советское радио», 1975, 200 с.), мощность метода кодирования равна числу неинверсных изоморфизмов. Для М-последовательностей мощность метода кодирования M_k равна числу невзаимных первообразных полиномов и определяется как:

где ϕ(…) - функция Эйлера;

обладают низкой структурной скрытностью вследствие наличия алгоритма Берлекэмпа-Месси. Для того, чтобы раскрыть ШПС, сформированный на базе М-последовательности, аналитику достаточно по известным, следующим подряд элементам последовательности, раскрыть всю ее структуру при помощи широко известного алгоритма Берлекэмпа-Месси (Алферов А.П. и др. Основы криптографии: учеб. пособие, 2-е изд., испр. и доп. М.: Гелиос АРВ, 2002, 480 с.).

Альтернативу М-последовательностям представляют, существующие в простых GF(p) и расширенных GF(pⁿ) полях Галуа, нелинейные рекуррентные последовательности (НЛРП) по следующим обстоятельствам:

НЛРП существуют для значительно большего числа длительностей L по сравнению с М-последовательностями, с шагом ΔL→1;

мощность кодирования у НЛРП намного больше, чем у М-последовательностей. Например, уже для простых характеристических НЛРП соотношение (1) будет иметь вид:

где простое число p>2, n=2, 3, … Отсюда видно, что уже для сравнимых по длительности L ПСП .

Ввиду отсутствия алгоритмов раскрытия структуры НЛРП, считается, что они абсолютно не раскрываемы, т.е. для того чтобы раскрыть структуру НЛРП, необходимо знать все ее символы .

2. Уровень техники

Известны способы раскрытия структуры ПСП:

1) основанные на знании закономерностей тонкой внутренней структуры ПСП.

Под тонкой внутренней структурой (ТВС) ПСП понимается закономерная структура взаимного расположения на длительности L дискретного сигнала (ДС) (рекуррентной последовательности) отдельных элементов и блоков, неделимых символов алфавита ДС. При этом неделимыми символами алфавита являются простейшие символы алфавита, а блоком является определенное число k_бл последовательно расположенных одинаковых символов.

Так, в (Варакин Л.Е. Системы связи с шумоподобными сигналами - М.: Радио и связь, 1985. - 384 с.) рассмотрен способ обнаружения ШПС, позволяющий различать случайную последовательность и М-последовательность и определять степень n полинома С(х), соответствующего вырабатывающему ее РСЛОС. В основе этого способа лежат особенности распределения вероятностей появления в М-последовательностях различных длительностей L блоков, состоящих из нулей.

2) основанные на знании особенностей правил построения и формирования (генерирования) ПСП.

Известен способ раскрытия структуры М-последовательности по ее символам при помощи алгоритма Берлекэмпа-Месси, основанный на построении регистра сдвига с линейной обратной связью (РСЛОС), порождающего заданную М-последовательность длительности L=2ⁿ-1 (Р. Галлагер. Теория информации и надежная связь. М.: «Советское радио», 1974, 720 с.; Блейхут Р. Теория и практика кодов, контролирующих ошибки. - М.: Мир, 1986. - 576 с.). Существование указанного способа обосновывает использование в системах связи различных технических средств усложнения аналитического строения М-последовательностей, к которым относятся, например, фильтрующие и комбинирующие генераторы, схемы с динамическим изменением закона рекурсии, схемы с элементами памяти и др. (Алферов А.П. и др. Основы криптографии: учеб. пособие, 2-е изд., испр. и доп. М.: Гелиос АРВ, 2002, 480 с.).

Работа алгоритма Берлекэмпа-Месси основана на том положении, что n+1 последовательных состояний РСЛОС линейно зависимы, и если символов М-последовательности заданы, то полином, задающий обратные связи, однозначно определен. То есть в данном случае алгоритм работает так: при заданном регистре, генерирующем последовательность μ₀…μ_i…μ_r-1, алгоритм проверяет, генерирует ли регистр последовательность μ₀…μ_i…μ_r, т.е. правильное значение следующего символа последовательности сравнивается со значением символа μ_r, действительно генерируемым регистром. Если значения и μ_r совпадают, тот r увеличивается на 1, а регистр остается неизменным. Если значения не совпадают, то к многочлену добавляется поправочный член так, чтобы символ μ_r генерировался правильно.

Для каждого r, начиная с r=1, строится РСЛОС, генерирующий первые r элементов М-последовательности μ₀…μ_i…μ_r. Затем r увеличивается на 1 и вычисляется выход предыдущего РСЛОС:

где c_j - коэффициенты полинома С(х), соответствующего построенному РСЛОС.

Вычисляется следующая разность d, которая показывает, соответствует ли действительное значение μ_r благоприятному :

где с₀=1.

Если d=0, то значения и μ_r совпадают, регистр остается неизменным. Если d=1, то значения и μ_r не совпадают, следовательно, необходимо модифицировать полином С(х). Новый полином будет иметь вид:

где В(х) - один из уже имеющихся полиномов С(х), вычисленных при последней r-ой операции, когда d было равно 1, а k - количество пройденных r-ых операций, при которых d равнялось 0:

После такой модификации d будет равно:

Работа алгоритма прекращается, когда r становится равным . Последний полином С(х), при котором d=1, соответствует РСЛОС минимальной длины, генерирующему заданную М-последовательность.

Алгоритм Берлекэмпа-Месси при восстановлении полинома С(х), задающего обратные связи РСЛОС, по символам М-последовательности, представлен на фиг. 1.

Однако указанный способ (алгоритм Берлекэмпа-Месси) является неприменимым для анализа и раскрытия структуры большого класса нелинейных псевдослучайных последовательностей и, как в частности, нелинейных рекуррентных последовательностей (НЛРП) (Сныткин И.И., Спирин А.В., Сныткин Т.И. Теоретическая концепция генерирования нелинейных рекуррентных последовательностей на основе использования регистров сдвига. - Международный научно-технический журнал «Нелинейный мир», №8, т. 11, 2013. - с. 531-539).

Построение НЛРП в полях GF(p) и GF(pⁿ) с двузначным характером отображения, например, μ={μ₁,μ₂,…,μ_i,…,μ_L}, где: μ_i={1;-1} или μ_i={1;0}; L={p,p-1,pⁿ-1} - длительность; p - простое число, p>2, - в общем случае связано с вычислением характера ψ(⋅) соответствующего элемента поля GF(q)={a₀,a₁,…,a_i,…,a_L-1}, где q - порядок поля (для GF(p) ⇒ q=p, а GF(pⁿ) ⇒ q=pⁿ), a_i - элементы поля (для GF(p) - числа от «0» до «р-1», для GF(pⁿ) - числа от «0» до «р-1» и полиномы f(x) степени не больше n), т.е. элементы μ_i есть:

где (для GF(p) приведение осуществляется по mod(p), а для GF(pⁿ) приведение осуществляется по двойному модулю modd(f^*(x),p), где f^*(x) - первообразный неприводимый полином для GF(pⁿ)); θ - первообразный элемент поля, причем при двузначном отображении:

Ввиду того, что длительность L НЛРП всегда удовлетворяет при некотором n неравенству 2^n-1-1<L<2ⁿ-1, т.е. всегда L≠2ⁿ-1, то циклические перестановки НЛРП μ={μ₁,μ₂,…,μ_i,…,μ_L} в совокупности с последовательностью μ={0,…,0} не могут сформировать абелеву группу относительно операции почленного сложения по модулю 2. Следовательно, НЛРП не обладают аддитивно-циклическим свойством, характерным для М-последовательностей, и не может быть найдено таких линейных логических обратных связей для РСЛОС, которые бы обеспечивали генерирование НЛРП заданной длительности L. Следовательно, структуру всей НЛРП невозможно раскрыть по определенному числу ее элементов при помощи алгоритма Берлекэмпа-Месси, как в случае с М-последовательностями.

Простейшим представителем НЛРП являются коды квадратичных вычетов (ККВ), построение которых базируется на использовании двузначного характера мультипликативной группы простого поля GF(p), с длительностью L=p и правилом построения в терминах характеров (Свердлик М.Б. Оптимальные дискретные сигналы. М.: изд-во «Советское радио», 1975, 200 с.):

В целях однозначного описания сходных признаков указанного способа раскрытия структуры М-последовательности с заявляемым способом раскрытия структуры НЛРП в виде ККВ, введем следующие определения и понятия:

Определение 1. Под характеристикой рекуррентной ПСП (РПСП) будем понимать какой-либо параметр или набор параметров, которые необходимо определять в процессе раскрытия структуры данной РПСП.

Так, следуя сущности алгоритма Берлекэмпа-Месси, характеристикой М-последовательности будет являться, соответствующий вырабатывающему ее РСЛОС, полином С(х) вида:

где c_j - коэффициенты полинома, n - степень полинома.

В (Сныткин И.И., Спирин А.В., Сныткин Т.И. Теоретическая концепция генерирования нелинейных…) определялось, что если i - номер элемента поля GF(p), то любой элемент - число a_i простого поля GF(p) может быть вычислен через предыдущий элемент a_i-1 и первообразный элемент θ согласно рекуррентного соотношения:

Решение задачи формирования ККВ связано с реализацией соотношения (12) и вычисления характеров ψ(a_i) элементов a_i мультипликативной группы поля GF(p).

Таким образом, для раскрытия структуры ККВ достаточно определить простое число p и соответствующий первообразный элемент θ. Однако, ввиду того, что значение характера ψ(a_i) элемента a_i мультипликативной группы поля GF(p) не зависит от выбранного первообразного элемента θ (Свердлик М.Б. Оптимальные дискретные сигналы. М: изд-во «Советское радио», 1975, 200 с.), то характеристикой ККВ будет являться только простое число р, значение которого будет равно, во-первых, количеству элементов поля GF(p), а во-вторых, длительности L данного кода.

Определение 2. Под действительным значением μ_r r-го символа РПСП понимается то его значение, которое вырабатывается устройством генерирования РПСП при заданной характеристике.

Определение 3. Под благоприятным значением r-го символа РПСП понимается то его значение, которое поступает на вход устройства для раскрытия структуры или обнаружителя, и не зависит от заданной характеристики данной РПСП.

Определение 4. Под входными данными Z₀ в данном случае понимается определенное число точно известных благоприятных значений последовательно расположенных элементов раскрываемой РПСП.

Сходными признаками известного способа раскрытия структуры М-последовательности по ее символам при помощи алгоритма Берлекэмпа-Месси с заявляемым способом являются следующие:

ввод входных данных Z₀ в виде определенного числа точно известных благоприятных значений последовательно расположенных элементов раскрываемой последовательности;

формирование (генерирование устройством) при заданной характеристике действительного значения μ_r r-ого символа последовательности;

сравнение действительного значения μ_r с благоприятным

Алгоритм Берлекэмпа-Месси при восстановлении полинома С(х), задающего обратные связи РСЛОС, по символам М-последовательности, имеет многочисленные общедоступные (в том числе в сети Internet) программные реализации. Схему построенного на регистрах сдвига устройства, реализующего данный алгоритм, можно найти, например, в (Блейхут Р. Теория и практика кодов, контролирующих ошибки. - М.: Мир, 1986. - 576 с.).

Техническая реализация указанных сходных признаков при осуществлении заявляемого способа раскрытия структуры НЛРП в виде ККВ, существующих в простых полях Галуа GF(p), требует возможности, во-первых, формирования элементов мультипликативной группы простого поля GF(p), и, во-вторых, формирования элементов μ_r ККВ различных длительностей L.

В (Сныткин И.И., Спирин А.В., Сныткин Т.И. Теоретическая концепция генерирования нелинейных…) также определялось, что если i - номер элемента a_i мультипликативной группы поля GF(p) и пробегает значения 1, 2, …, р-2, то формирование НЛРП в виде ККВ означает позициям μ_i присваивать значения меандра ψ(a_i) ∈ {0,1} на позициях i=a_i.

Таким образом, формирование ККВ фиксированных длительностей представляет собой генерирование меандра ψ(a_i) ∈ {0,1} с управлением по тактам i. Данный технический замысел реализован в устройствах формирования НЛРП (Устройство формирования словарей нелинейных рекуррентных последовательностей // Авторское свидетельство СССР №2024053, опубл. 30.11.1994. Бюл. №22; Устройство формирования кодовых словарей нелинейных рекуррентных последовательностей // Патент RU 2439657 С2, опубл. 10.01.2012. Бюл. №1; Устройство для формирования имитостойких нелинейных рекуррентных последовательностей // Патент RU 2574805 С1, опубл. 10.02.2016. Бюл. №4). Однако данные устройства обеспечивают формирование НЛРП только фиксированных длительностей и не могут быть использованы для решения задачи раскрытия структуры НЛРП произвольных длительностей.

Формирование ККВ произвольных длительностей возможно за счет включения в схему устройства элемента памяти, в котором значение меандра ψ(a_i) ∈ {0,1} будет записываться по адресу, соответствующему значению элемента a_i мультипликативной группы поля GF(p) (Устройство для формирования псевдослучайных сигналов // Авторское свидетельство СССР №995292, опубл. в Б.И. 1983. Бюл. №5). В данном случае, считывание последовательности возможно только после того, как она будет полностью сформирована, и следовательно, не представляется возможным воспроизведение всей последовательности по определенному числу ее элементов.

Поэтому целесообразным путем технической реализации устройства для раскрытия структуры ККВ является использование средств формирования элементов мультипликативной группы поля GF(p).

Решение задачи формирования последовательности элементов мультипликативных групп как простых GF(p), так и расширенных GF(pⁿ) полей Галуа было осуществлено в рамках ряда устройств (А.С. №849895 (СССР). Устройство для формирования элементов мультипликативных групп полей Галуа // Сныткин И.И., Долгов В.И., Горбенко И.Д.; А.С. №1236497 (СССР). Устройство для формирования элементов мультипликативных групп полей Галуа // Сныткин И.И., Петренко В.И. - опубл. в Б.И. 1986, №21; А.С. №1334982 (СССР). Устройство для формирования элементов мультипликативных групп полей Галуа // Сныткин И.И., Горбенко И.Д., Ткач А.А.).

Устройство для формирования элементов мультипликативных групп полей Галуа GF(p) (Патент RU 2007032 С1, опубл. 30.01.1994, Бюл. №28) предназначено для использования в устройствах формирования кодовых рекуррентных последовательностей, существующих в простых полях Галуа GF(p), что позволяет считать данное устройство близким аналогом (прототипом) к заявляемому устройству. Однако данное устройство не позволяет решать задачу раскрытия структуры НЛРП в виде ККВ, существующих в простых полях Галуа GF(p).

Сходными признаками данного устройства (прототипа) с заявляемым устройством являются:

устройство содержит: первый и второй блок элементов ИЛИ, схему сравнения, вычитатель, первый и второй формирователи импульсов, элемент задержки, первый и второй регистры хранения, элемент ИЛИ, блок умножения, первый и второй блоки и элементов И, с соответствующими связями.

3. Раскрытие изобретения

Как известно, схема произведения квадратичных вычетов и невычетов аналогична схеме сложения для «четного и нечетного» (Хассе Г. Лекции по теории чисел. - М.: изд-во Наука, 1953. - 528 с.), следовательно, для любых элементов ККВ μ={μ₀,…,μ_i,…,μ_j,…,μ_p-1} всегда будет выполняться:

Таким образом, полностью раскрыть структуру НЛРП в виде ККВ можно на основе тех его элементов μ_i, номера i которых соответствуют простым числам, так как остальные элементы, номера k которых соответствуют составным числам, являются результатом произведения (13).

Если ограничить сверху максимально возможную длительность L_max последовательности (т.е. длительность L раскрываемой НЛРП в виде ККВ будет лежать в пределах 5≤L<L_max), то количество всех возможных ККВ в этом промежутке будет определяться функцией π(L_max) распределения простых чисел, равной числу простых чисел, меньших максимально возможной длительности последовательности L_max. При определении числа p элементов поля GF(p) каждый известный элемент μ_i ККВ, номер i которого соответствует простому числу, будет уменьшать область поиска в 2 раза, и количество N необходимых для раскрытия структуры элементов ККВ μ_i, номера i которых соответствуют простым числам, будет определяться соотношением:

Количество же элементов ККВ , необходимых для раскрытия его структуры, будет равно значению простого числа Q, имеющего порядковый номер N:

Единица в выражении (15) добавляется ввиду того, что необходимо учитывать первый элемент ККВ μ₀=0.

Например, для того чтобы раскрыть структуру ККВ, максимально возможная длительность L_max которого равна L_max=131, необходимо точно знать символов последовательности (см. пример на фиг. 5).

Так как для раскрытия структуры М-последовательности аналитику достаточно точно знать следующих подряд ее элементов, то абсолютная Z_a6c и относительная Z_отн сложности раскрытия структуры М-последовательности в зависимости от длительности L соответственно равны Z_a6c=2n, Z_отн=2n/2ⁿ-1.

Для НЛРП в виде ККВ абсолютная Z_a6c и относительная Z_отн сложности раскрытия структуры при помощи заявляемого способа в соответствии с соотношением (15) представляют графики зависимостей, изображенные на фиг. 2.

Существенными отличительными признаками заявляемого способа от способа (прототипа) раскрытия структуры М-последовательности по ее символам при помощи алгоритма Берлекэмпа-Месси являются следующие:

простому числу p, являющемуся характеристикой кода квадратичных вычетов, присваивается минимальное значение:

,

где L_max - максимально возможная длительность последовательности, π(L_max) - количество простых чисел, меньших L_max, Q - значение простого числа, имеющего порядковый номер N=log₂π(L_max);

вычисляется значение минимального первообразного элемента θ по модулю простого числа p;

в соответствии с рекуррентным соотношением a_i=a_i-1⋅θ(modp) формируется последовательность элементов мультипликативной группы поля GF(p), GF(p)={а₁,а₂,…,a_i=r}, до получения значения элемента a_i, равного номеру r элемента поступившей последовательности;

при разнице действительного значения μ_r с благоприятным значение числа p увеличивается до следующего простого значения p*, формируется последовательность элементов мультипликативной группы поля GF(p*), GF(p*)={a₁*,a₂*,…,a_i*=r}, до получения значения элемента a_i*, равного номеру r элемента поступившей последовательности;

если действительное значения μ_r равно благоприятному , значение числа p не изменяется, r увеличивается на единицу, заново формируется последовательность элементов мультипликативной группы поля GF(p), GF(p)={a₁,а₂,…,a_i=r}, до получения значения элемента a_i, равного номеру r+1 элемента поступившей последовательности, пока уже значения μ_r+1=ψ(a_i=r+1) и не будут равны;

когда r становится равным , выводится значение простого числа p, являющегося характеристикой раскрываемой нелинейной рекуррентной последовательности в виде кода квадратичных вычетов, существующих в простых полях Галуа GF(p).

4. Краткое описание чертежей

На фиг. 1 изображен алгоритм Берлекэмпа-Месси при восстановлении полинома С(х), задающего обратные связи РСЛОС, по символам М-последовательности.

На фиг. 2 изображены графики зависимости абсолютной Z_a6c и относительной Z_o сложности раскрытия структуры ККВ от его длительности L (пунктиром показаны графики указанной зависимости без учета заявляемого способа).

На фиг. 3 изображен алгоритм раскрытия структуры нелинейных рекуррентных последовательностей в виде кодов квадратичных вычетов, существующих в простых полях Галуа GF(p).

На фиг. 4 изображено главное окно программы для демонстрации работы способа раскрытия структуры нелинейных рекуррентных последовательностей в виде кодов квадратичных вычетов, существующих в простых полях Галуа GF(p).

На фиг. 5 изображен пример раскрытия структуры кода квадратичных вычетов (L=p=67) по символам последовательности.

На фиг. 6 изображена функциональная схема устройства для раскрытия структуры нелинейных рекуррентных последовательностей в виде кодов квадратичных вычетов, существующих в простых полях Галуа GF(p).

5. Осуществление изобретения

Заявляемый способ характеризуется в приведенном на фиг. 3 алгоритме следующей совокупностью последовательных действий (этапов):

Этап 1. Ввод данных (блоки 2 и 3 на фиг. 3).

Набором входных данных Z₀ является определенное число точно известных благоприятных значений последовательно расположенных элементов раскрываемой НЛРП в виде ККВ.

К примеру, если принятый ШПС является фазоманипулированным НЛРП в виде ККВ сигналом, то после демодуляции он превращается в двоичную последовательность, которая в виде определенного числа точно известных благоприятных значений символов ККВ последовательно поступает на вход устройства для раскрытия структуры РПСП.

Простому числу р, являющемуся характеристикой кода квадратичных вычетов, присваивается значение:

,

где L_max - максимально возможная длительность последовательности, π(L_max) - количество простых чисел, меньших L_max, Q - значение простого числа, имеющего порядковый номер N=log₂π(L_max).

Далее вычисляется значение минимального первообразного элемента θ по модулю простого числа р.

Переменной r присваивается значение номера элемента поступившей последовательности (если отрезок ККВ начинается с начала последовательности, то целесообразно переменной r присвоить значение числа 2, так как μ₀=0, а в соответствии со свойствами двузначного характера μ₁=1).

Этап 2. Формирование последовательности элементов мультипликативной группы поля GF(p), GF(p)={а₁,а₂,…,a_i=r}, до получения значения элемента a_i, равного номеру r элемента поступившей последовательности, а также формирование действительного значения μ_r r-ого элемента ККВ при заданной характеристике p (блоки 4-8 на фиг. 3).

Первому элементу a₁ мультипликативной группы поля GF(p) присваивается значение числа 1. Одновременно двузначному характеру у присваивается значение 1.

Затем в соответствии с рекуррентным соотношением:

a_i=a_i-1⋅θ(modp)

циклически с каждым шагом i=2, 3… происходит вычисление значения следующего элемента a_i мультипликативной группы поля GF(p), сравнение его со значением номера r элемента поступившей последовательности и изменение значения двузначного характера у на противоположное.

Таким образом, к моменту формирования элемента a_i мультипликативной группы поля GF(p), равного номеру r элемента поступившей последовательности, будет сформировано действительное значение r-ого элемента ККВ при заданной характеристике p:

μ_r=ψ(a_i=r),

что полностью соответствует правилу (10) построения ККВ в терминах характеров.

Этап 3. Сравнение действительного значения μ_r с благоприятным (блок 9 на фиг. 3).

Если значения μ_r=ψ(a_i=r) и различны, то число p не удовлетворяет отрезку поступившей последовательности. Значение числа p увеличивается до следующего простого значения p*. Вычисляется значение минимального первообразного элемента θ* по модулю простого числа p*, числу r присваивается значение 2 (блок 10 на фиг. 3).

Последовательно выполняются этапы 2 и 3, пока значения μ_r и не будут равны.

Если же значения μ_r=ψ(a_i=r) и равны, то число p удовлетворяет данному отрезку последовательности, r увеличивается на единицу (блок 12 на фиг. 3), и заново выполняются этапы 2 и 3, пока уже значения μ_r+1=ψ(a_i=r+1) и не будут равны.

Работа алгоритма прекращается, когда r становится равным (блок 11 на фиг. 3). Последнее значение простого числа p*, при котором , является характеристикой раскрываемого ККВ.

В целях проверки завершаемости (конечности) и результативности заявляемого способа раскрытия структуры НЛРП в виде ККВ, была составлена демонстрационная программа на языке Delphi, позволяющая по установленному ограничению максимальной длительности L последовательности определять количество необходимых для раскрытия структуры НЛРП в виде ККВ точно известных благоприятных значений последовательно расположенных элементов последовательности, а также на основе известности данных благоприятных значений раскрывать структуру всего кода.

Главное окно программы представлено на фиг. 4.

Целью, достигаемой устройством для раскрытия структуры нелинейных рекуррентных последовательностей в виде кодов квадратичных вычетов, существующих в простых полях Галуа GF(p), является расширение функциональных возможностей устройства для формирования элементов мультипликативных групп полей Галуа GF(p) по выполнению функции раскрытия структуры НЛРП в виде ККВ.

Цель достигается тем, что в устройство для формирования элементов мультипликативных групп полей Галуа GF(p), содержащее первый и второй блок элементов ИЛИ, первую схему сравнения, вычитатель, первый и второй формирователи импульсов, первый элемент задержки, первый и второй регистры, элемент ИЛИ, блок умножения, первый и второй блоки элементов И, объединенные в блок формирования элементов мультипликативной группы поля (БФЭМГП), причем входы первой группы вычитателя соединены соответственно с выходами второго блока элементов ИЛИ, входы первой группы которого соединены соответственно с входами первой группы первого блока элементов ИЛИ и с выходами второго блока элементов И, входы второй группы которого соединены с выходами результата блока умножения, выход окончания умножения которого соединен с входами первой группы второго блока элементов И и со вторым входом элемента ИЛИ, выход которого соединен с входом элемента задержки, выход которого соединен с управляющим входом схемы сравнения, выход "меньше" которой соединен с входом разрешения записи первого регистра, выход вычитателя соединен с информационным входом второго регистра, разрядные выходы которого соединены соответственно с входами первой группы первого блока элементов И, выходы которого соединены соответственно с входами второй группы второго блока элементов ИЛИ и входами второй группы первого блока элементов ИЛИ, выходы которого соединены соответственно с входами первой группы схемы сравнения и информационными входами первого регистра, разрядные выходы которого соединены соответственно с входами регистра множимого блока умножения, выход "больше" схемы сравнения соединен с управляющим входом вычитателя и входом первого формирователя импульсов, выход которого соединен с входом разрешения записи второго регистра хранения и с входом второго формирователя импульсов, выход которого соединен с входами второй группы первого блока элементов И и первым входом элемента ИЛИ, введены: Т-триггер, D-триггер, счетчик, вторая схема сравнения, объединенные в блок формирования элементов кода, второй и третий элементы ИЛИ, второй и третий элементы задержки, блок управления, третья схема сравнения, причем вход записи элемента поступившей последовательности соединен с пятым входом блока управления, первый выход которого соединен со входом обнуления блока умножения, входом третьего элемента задержки и установочным входом Т-триггера, выход которого соединен с информационным входом D-триггера, выход которого соединен со вторым информационным входом третьей схемы сравнения, вход запуска устройства соединен с шестым входом блока управления и первым входом третьего элемента ИЛИ, выход которого соединен с установочным входом счетчика, выход третьего элемента задержки соединен с первым входом второго элемента ИЛИ, выход которого соединен со входом запуска блока умножения, выходы второй группы блока управления соединены соответственно с входами регистра множителя блока умножения, выходы третьей группы блока управления соединены соответственно со второй группой входов вычитателя, выходом значения простого числа устройства и второй группой входов первой схемы сравнения, выход "меньше" которой соединен с информационным входом Т-Триггера и управляющим входом второй схемы сравнения, выход "равно" которой соединен со входом синхронизации D-триггера и входом второго элемента задержки, выход которого соединен с управляющим входом третьей схемы сравнения, выход "равно" которой соединен с выходом ввода следующего элемента последовательности устройства и счетным входом счетчика, разрядные выходы которого соединены соответственно с первой группой входов второй схемы сравнения, выход "не равно" которой соединен со вторым входом второго элемента ИЛИ, разрядные выходы первого регистра соединены со второй группой входов второй схемы сравнения, четвертый выход блока управления соединен с первым входом третьей схемы сравнения, выход "не равно" которой соединен с седьмым входом блока управления и вторым входом третьего элемента ИЛИ.

Функциональная схема устройства для раскрытия структуры НЛРП в виде ККВ, существующих в простых полях Галуа GF(p), представлена на фиг. 6.

Устройство содержит:

блок 1 формирований элементов мультипликативной группы поля GF(p) (БФЭМГП), содержащий: первый и второй 3 и 5 блоки элементов ИЛИ, схему 4 сравнения, вычитатель 6, первый и второй 7 и 11 формирователи импульсов, первый элемент 8 задержки, первый и второй 9 и 10 регистры, элемент 12 ИЛИ, блок 13 умножения, первый и второй блоки 14 и 15 элементов И;

блок 2 формирования элементов кода (БФЭК), содержащий: Т-триггер 16, D-триггер 17, счетчик 18, схему 19 сравнения;

второй и третий 20 и 21 элементы ИЛИ; второй и третий элементы 22 и 23 задержки; блок 24 управления (БУ); третью схему 25 сравнения; с соответствующими функциональными связями.

Устройство работает следующим образом.

Начало выполнения этапа 1 ввода данных осуществляется подачей благоприятного значения r-ого символа поступившей последовательности на вход 27 устройства. На вход 28 запуска устройства поступает импульс «Начало работы», который, проходя на шестой вход БУ 24, включает его, обеспечивая запись в него r-ого символа поступившей последовательности, а также, пройдя через элемент 21 ИЛИ, поступает на установочный вход счетчика 18, сбрасывая его в состояние «r», что соответствует номеру элемента поступившей последовательности. После окончания записи поступившего символа БУ 24 формирует с выхода 1 импульс, который обнуляет регистр множителя блока умножения 13 БФЭМГП, устанавливает Т-триггер 16 БФЭК 2 в состояние «1». В регистр множимого блока умножения 13 записывается единица. На выходе 3 БУ 24 формируется код модуля р, который поступает на входы B_n схемы 4 сравнения и на вторые входы вычитателя 6. На вторые входы б