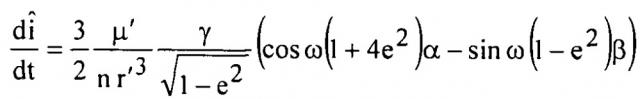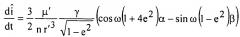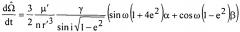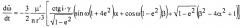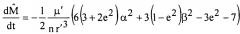Способ ограничения засорения эксплуатируемых областей околоземного космического пространства

Способ ограничения засорения эксплуатируемых областей околоземного космического пространства

Иллюстрации

Показать все

Реферат

Изобретение относится к области космической техники, а именно к решению проблемы противодействия техногенному засорению интенсивно эксплуатируемых областей околоземного космического пространства (ОКП). Может быть использовано для ограничения и очистки ОКП от прекративших активное существование космических аппаратов, их обломков, отделившихся частей последних ступеней ракет-носителей и разгонных блоков (РБ).

Объекты ракетно-космической техники (РКТ), обеспечившие выведение полезной нагрузки на целевые геосинхронные орбиты (ГСО), остаются в космосе на определенных орбитах в соответствии с реализуемыми схемами их выведения. Становясь бесполезным крупногабаритным космическим мусором (ККМ) и накапливаясь в характерных областях космического пространства, связанных с выведением на ГСО по типовым схемам, отработавшие объекты РКТ могут создавать реальные угрозы для безопасности последующих запусков космических аппаратов (КА) на ценные и интенсивно эксплуатируемые геосинхронные орбиты. Наиболее засорены те области орбит вокруг Земли, которые чаще всего используются для работы космических аппаратов. Причем, вокруг Земли в настоящее время уже имеются три слоя космического мусора (Вениаминов С.С., Червонов A.M. Космический мусор - угроза человечеству, Москва, 2012, ИКИ РАН - [Д1]):

около 300-400 км от поверхности Земли;

около 1500-1700 км от поверхности Земли;

около 36000 км от поверхности Земли.

В частности, отработавшие разгонные РБ, ставшие неуправляемым объектами ККМ, заслуживают особого внимания, как в плане их возможных непосредственных столкновений с выводимыми или функционирующими на ГСО КА, так и в плане возможных разрушений таких объектов с последующим крупномасштабным засорением используемых областей космического пространства (эффект Кесслера) - [Д1]. Для того чтобы избежать столкновений с КА на ГСО, данные РБ переводят на так называемые орбиты увода, у которых высота в апоцентре меньше высоты ГСО. Ввиду того, что переводимые на орбиты увода РБ засоряют области, используемые для геопереходных операций при выведении КА на ГСО, необходимо знать, как будут эволюционировать такие орбиты, и как долго будут существовать в космосе переведенные на них РБ.

Поэтому разработка и внедрение мероприятий, направленных на снижение засоренности ОКП техногенными объектами космической деятельности, является одной из самых приоритетных задач настоящего времени и будет иметь чрезвычайный характер в ближайшем будущем [Д1].

Идеальным вариантом противодействия техногенному засорению интенсивно эксплуатируемых областей ОКП, в частности, областей, используемых для выведения КА на ГСО, является ограничение его засоренности путем выбора для отработавших объектов РКТ таких орбит увода, на которых эти объекты будут иметь ограниченное время существования.

В соответствии с рекомендациями Руководящих принципов по предотвращению техногенного засорения околоземного космического пространства, принятых международным сообществом (Руководящие принципы предупреждения образования космического мусора, разработанные Международным координационным комитетом по космическому мусору. Комитет ООН по использованию космического пространства в мирных целях, Научно-технический подкомитет. Сороковая сессия. 2003 год. A/AC.105/C.2/L.260), космические аппараты, выработавшие своей ресурс и прекратившие активное существование, должны освободить место на геостационарной орбите путем удаления этих аппаратов на орбиту захоронения.

В настоящее время предложены 12 подходов (способов) решения проблемы уменьшения и ограничения засорения околоземного космического пространства (http://www.gpclub.ru/9739.html - [Д2]), являющиеся аналогами данного изобретения,

1. Оборудование спутников дополнительным баком горючего, который будет выводить их дальше в космос или направлять в слои атмосферы для сгорания.

2. Разработка и применение роботизированных уборщиков-камикадзе CleanSpace One - спутник с «рукой», хватающий обломок и перемещающийся с ним в слои атмосферы, где они оба сгорают.

3. Способ уничтожения лазерными лучами. Минус такой уборки - невозможность полностью сжечь металл, а сплавы могут причинять еще большую опасность.

4. Использование облака из баллистического газа. Детище компании Boeing, спутник с генератором газа, планируется вывод на орбиту и в противоположную сторону от вращения всех тел, после чего выпускается облако, врезавшись в которое мусор будет спускаться и сгорать в атмосфере.

5. Разработка и использование космического траулера, ловящего мусор в своеобразные сети.

6. Использование статического электричества, выталкивающего мусор дальше в космическое пространство, при этом зарядка мусора электронами возлагается на беспилотник типа GLiDer.

7. Встраивание в корпус спутника наполняемого гелием воздушного шара, на который после окончания срока эксплуатации спутника возлагается увод в зону захоронения.

8. Разработка и использование роботов - ремонтников, отлавливающих спутники, и разбирающих их на запчасти, при этом пригодные для эксплуатации детали планируется возвращать на Землю или устанавливают в другие спутники.

9. Использование космического пылесоса от корпорации «Энергия», представляющего собой огромный буксир с крематорием, куда будет собираться мусор и сжигаться.

10. Разработка и использование электродинамического трала (Япония), оснащаемого магнитной сеткой для сбора металлических объектов, при наполнении трал вместе с мусором сгорит в атмосфере, недостатки: собирает КМ только низких орбитах и только то, что намагничивается.

11. Использование гарпуна с ловушкой, разработка инженеров фирмы Astrium (ЕКА). Спутник планируется за космическим мусором, и выстреливать в него гарпуном с ловушкой, после чего сеть с мусором будет доставлена для сожжения в атмосферу, а робот-охотник продолжит свою уборку.

12. Буксир Terminator Tether - в спутник встроят проволоку с устройством. После их поломки, катушка будет раскручена, а спутник отбуксирован в слои атмосферы.

Реализация предлагаемых способов относится к космическим средствам и системам с действиями активного характера по очищению ОКП от ККМ и связана с разработкой специальных орбитальных спутников-уборщиков со сложнейшим оборудованием, с трудоемкими и сложными в исполнении операциями на орбите. Недостатками вышеприведенных аналогов являются техническая сложность создания и обеспечения управления космическими аппаратами для расчистки космического пространства, особенно в интенсивно эксплуатируемых областях ГСО, а также высокие затраты на разработку и выведение специализированных космических аппаратов по уводу ККМ на орбиты захоронения, причем данные способы реализуют только увод ККМ на орбиты захоронения или в атмосферу для их сгорания, и не способствуют ограничению засорения интенсивно эксплуатируемых областей ОКП. Причем, как правило, на каждый объект ККМ необходим один специализированный КА, например, космический буксир.

Наиболее близким по технической сущности к предлагаемому изобретению в части функционального предназначения (прототипом) выбран «Способ увода космического мусора с орбит полезных нагрузок на основе использования отделившейся части ракеты-носителя, разгонного блока и устройство для его реализации», патент №2462399 RU, - [Д3]. Технический результат прототипа заключается в том, что с помощью отделяемого от отделившихся частей (ОЧ) последней ступени ракет-носителей (РН) или разгонного блока (РБ) малоразмерного космического буксира (МКБ), связанного механической связью с ОЧ РН или РБ тросом, осуществляют стыковку МКБ с космическим мусором, после чего прилагают тормозной импульс к ОЧ ступени РН или РБ на основе использования невыработанных запасов жидкого топлива для увода связки «ОЧ ступени РН, РБ - трос - МКБ - космический мусор» на орбиту утилизации.

Недостатком прототипа является необходимость разработки и использования специального космического аппарата, создаваемого только для выполнения одной лишь функции - расчистки космического пространства от космического мусора, что является высокозатратным и трудноосуществимым, особенно при проведении операций в дальнем Космосе, к тому же использование данного способа обеспечивает только увод ККМ на орбиты захоронения, что не способствует ограничению засорения интенсивно эксплуатируемых областей ОКП. Следует отметить, что по способу-прототипу возможна расчистка и увод на орбиты захоронения от одного (на орбитах ГСО) до нескольких (на низких и средних околоземных орбитах) объектов ККМ. Все зависит от орбит увода и затрат топлива на совершение маневров буксира.

Целью данного изобретения является ограничение засорения завершившими свою миссию объектами ракетно-космической техники в интенсивно эксплуатируемых областях ОКП, в том числе и в областях, используемых для выведения КА на геосинхронные орбиты.

Сущность изобретения заключается в том, что на основе проведения качественного анализа долговременной эволюции орбит осуществляют выбор таких орбит увода завершивших свою миссию объектов ракетно-космической техники, на которых эти объекты будут иметь ограниченное время существования. Для этого используют предложенные авторами сравнительно несложные аналитические зависимости, с помощью которых осуществляют качественный анализ долговременной эволюции орбит увода отработавших РБ из области ГСО и оценивают время существования ККМ на таких орбитах в зависимости от начальных параметров этих орбит.

Технический результат предложенного изобретения заключается в обоснованном выборе орбиты увода завершивших свою миссию объектов ракетно-космической техники на основе оценки времени их баллистического существования путем использования предложенных аналитических зависимостей, позволяющих рассчитывать долговременную эволюцию орбит увода с учетом влияния различных возмущающих факторов в зависимости от исходных параметров таких орбит и времени начала движения по ним завершивших свою миссию объектов ракетно-космической техники.

Указанный технический результат достигается тем, что в заявленном способе оценку времени баллистического существования выбираемых орбит для увода завершивших свою миссию объектов ракетно-космической техники проводят с использованием аналитических зависимостей, позволяющих рассчитывать долговременную эволюцию орбит увода. Эти расчеты проводят по шагам с учетом влияния на объекты ракетно-космической техники различных возмущающих факторов в зависимости от исходных параметров таких орбит и времени начала движения по ним завершивших свою миссию объектов ракетно-космической техники. При этом на первом шаге вычисляют и оценивают вековые изменения угловых элементов орбит увода, а именно долготы восходящего узла - Ω, аргумента перицентра - ω и средней аномалии в эпоху - М₀, вызываемые нецентральностью гравитационного поля Земли, где основным фактором является влияние динамического сжатия Земли, значения которых вычисляют по формулам:

,

,

,

где: коэффициенты , , определяют скорость соответствующих вековых изменений, J₂ - коэффициент при второй зональной гармонике в разложении гравитационного потенциала Земли в ряд по сферическим функциям, а - большая полуось орбиты, е - ее эксцентриситет, i - наклонение орбиты к экватору Земли, a_e - экваториальный радиус Земли, - среднее движение, μ - гравитационная постоянная Земли.

На шаге 2 вычисляют и оценивают изменения осредненных элементов орбит из-за притяжения третьего тела (Луны и/или Солнца) с использованием результатов решения следующих уравнений:

, ,

,

,

,

,

где μ', r' - гравитационная постоянная и геоцентрическое расстояние третьего тела, α, β, γ - направляющие косинусы, определяющие направление на третье тело в орбитальной системе координат ξηζ, начало которой О находится в центре Земли, плоскость ξη совпадает с плоскостью орбиты КА в начальный момент времени, ось ξ направлена в перицентр орбиты π, ось ζ - ортогональна плоскости орбиты и ось η - дополняет систему до правой.

На шаге 3 определяют влияние аэродинамического сопротивления атмосферы на участках орбит увода, находящихся в сфере ее действия, интегральный эффект которого за виток представляют в виде определенного импульса скорости ΔV, прикладываемого в направлении, противоположном скорости V_π космического объекта в перицентре его орбиты, что влечет за собой изменение большой полуоси и эксцентриситета орбиты на величины Δa и Δe согласно зависимостям:

, ,

где μ_З - гравитационная постоянная Земли.

На шаге 4 оценивают время существования орбиты увода, которое характеризуется таким изменением в результате эволюции высоты ее перицентра Н_π, когда достигается выполнение условия Н_π<80 км и космический объект входит в плотные слои атмосферы, при этом изменения этой высоты оценивают с использованием зависимости δH_π=δa(l-e)-a δe, которую, с учетом того, что δa=0, сводят к оценке изменения δe за счет притяжения Солнца, получаемой в результате решения уравнения:

,

где изменяемое во времени произведение αβ вычисляют по формуле:

,

в которой значения элементов i', Ω' траектории третьего тела (Солнца), и его широты u' относительно орбитальной системы координат ξηζ, у которой ось ξ направлена в перицентр орбиты, ось ζ - ортогональна плоскости орбиты и ось η дополняет систему координат до правой, получают на основании соотношений:

,

,

cos I=cosi⋅cosi'-sini⋅sini'cos(ω+Ω').

,

,

где i, Ω, ω - параметры рассматриваемой орбиты увода и I, и - наклонение, долгота восходящего узла и широта орбиты возмущающего тела (Солнца) относительно базовой геоцентрической экваториальной системы координат XYZ.

На шаге 5 для получения искомых оценок принимают, что I≅23°.43472, , широта изменяется со временем согласно зависимости , где t₀ - время ближайшего к t момента весеннего равноденствия, приходящееся обычно на 20-21 марта каждого года, причем для анализа характера изменения эксцентриситета е выбираемой орбиты увода в зависимости от положения проекции направления на Солнце на плоскость орбиты в орбитальной системе координат ξηζ вырабатывают следующее правило. Эксцентриситет е орбиты увода будет уменьшаться, а высота ее перигея Н_π соответственно возрастать, когда α и β имеют одинаковый знак, что имеет место, когда проекция направления на возмущающее тело на плоскость ξη орбитальной системы координат находится в первом или в третьем квадранте этой плоскости, и наоборот, эксцентриситет е будет увеличиваться, а Н_π - уменьшаться в случае, когда α и β имеют разные знаки, то есть, при нахождении проекции направления на возмущающее тело во втором или четвертом квадранте базовой плоскости ξη. Причем, указанное правило применяют при выборе ориентации орбиты увода относительно направления на Солнце и начала движения по ней отработавшего объекта ракетно-космической техники так, чтобы с учетом движения Солнца вокруг Земли и изменения положения плоскости орбиты в пространстве за счет влияния возмущающих факторов можно было бы добиться максимального времени нахождения проекции направления на Солнце на плоскость орбиты в тех квадрантах базовой плоскости ξη орбитальной системы координат, где направляющие косинусы α и β имеют разные знаки, и происходит возрастание величины эксцентриситета е выбираемой орбиты увода, что приводит к уменьшению высоты перицентра H_π, а в итоге к искомому уменьшению времени баллистического существования на выбранной орбите увода космических объектов в области геопереходных орбит.

Заявленный способ ограничения засорения эксплуатируемых областей околоземного космического пространства основывается на предварительно выполненном анализе и результатах исследований, связанных с изучением эволюции высокоэллиптических орбит ИСЗ на длительных интервалах времени [Д4, Д5]. Анализ и результаты исследований показали, что основными возмущающими факторами для орбит увода из области ГСО являются нецентральность гравитационного поля Земли и гравитационное притяжение со стороны третьих тел - Луны и Солнца. Кроме того, для орбит увода с низкими высотами перицентра, находящимися в пределах действия верхней атмосферы, заметное влияние на изменение их параметров может оказывать сопротивление атмосферы. Способ ограничения засорения эксплуатируемых областей ОКП поясняется совокупностью и порядком выполнения действий (шагов) по достижению указанной цели. Такими шагами являются:

- оценка влияния нецентральности гравитационного поля Земли на долговременную эволюцию орбит увода;

- оценка влияния лунно-солнечных возмущений на изменение параметров орбит увода;

- оценка влияния сопротивления атмосферы на изменение высокоэллиптических орбит увода;

- оценка времени существования ККМ на орбитах увода из области ГСО;

- установление зависимости времени существования ККМ на орбитах увода от начальных параметров и условий движения по этим орбитам.

Шаг 1: Оценка влияния нецентральности гравитационного поля Земли на долговременную эволюцию орбит увода

Аналитические оценки и численные расчеты свидетельствуют, что основным возмущающим фактором со стороны нецентрального гравитационного поля Земли, наиболее существенно влияющим на долговременную эволюцию параметров орбит увода из области ГСО, является вторая зональная гармоника в разложении гравитационного потенциала Земли в ряд по сферическим функциям. Влияние этой гармоники приводит к изменениям (возмущениям) всех элементов орбит ИСЗ; такие возмущения по своей природе делятся на короткопериодические, долгопериодические и вековые. Доказано, что с точностью до второго порядка малости относительно значения коэффициента J₂ при этой гармонике (J₂=0.001082), она не вызывает вековых и долгопериодических возмущений в большой полуоси орбиты ИСЗ. Влияние данной гармоники не приводит также к вековым возмущениям в эксцентриситете и наклонении орбиты ИСЗ, хотя эти параметры и претерпевают долгопериодические возмущения.

Вековые изменения за счет влияния второй зональной гармоники происходят лишь в угловых элементах орбиты: долготе восходящего узла - Ω, аргументе перицентра - ω и в средней аномалии в эпоху - М₀. Эти возмущения могут быть представлены в виде:

, , ,

где t, t₀ - текущий и начальный моменты времени, а коэффициенты , , определяют скорость соответствующих вековых изменений, С точностью до первого порядка относительно J₂ эти коэффициенты определяются следующим образом [Д6]:

Здесь а - большая полуось орбиты, е - ее эксцентриситет, i - наклонение орбиты к экватору Земли (базовой плоскости используемой геоцентрической системы координат), a_e - экваториальный радиус Земли, - среднее движение, μ - гравитационная постоянная Земли.

Из приведенных формул следует, что вековые изменения угловых элементов Ω, ω и М₀ будут уменьшаться по мере увеличения большой полуоси орбиты и возрастать при увеличении ее эксцентриситета. Так, в таблице 1 приведены значения скоростей изменения указанных угловых параметров для возможных орбит увода из области ГСО, имеющих высоту в апоцентре Н_α=35700 км и наклонение i=0, в зависимости от высоты перицентра Н_π этих орбит.

Шаг 2: Оценка влияния лунно-солнечных возмущений на изменение параметров орбит увода

Для учета гравитационного воздействия на ККМ, находящегося на орбите ИСЗ, со стороны третьего тела (Луны или Солнца) введем в рассмотрение возмущающую функцию R, зависящую как от элементов орбиты ККМ, так и от положения возмущающего тела в пространстве. Данная функция определяется следующей зависимостью:

где μ' - гравитационная постоянная возмущающего тела, r, r' - расстояние от центра Земли до ККМ и возмущающего тела соответственно, Ψ - угол между направлениями на ККМ и на третье тело.

Введем в рассмотрение орбитальную систему координат ξηζ, начало которой О находится в центре Земли, плоскость ξη совпадает с плоскостью орбиты КА в начальный момент времени, ось ξ направлена в перицентр орбиты π, ось ζ - ортогональна плоскости орбиты и ось η - дополняет систему до правой. Положение ККМ в данной системе определяется вектором {r cos ϑ, r sin ϑ, 0}, где ϑ - истинная аномалия, отсчитываемая в плоскости движения КА от направления на перицентр π.

Обозначим через α, β, γ направляющие косинусы, определяющие направление на возмущающее тело в орбитальной системе координат, так что:

и , , - единичные орты системы координат ξηζ.

После введенных обозначений косинус угла между векторами и будет определяться соотношением

cosΨ=αcosϑ+βsinϑ.

Координаты единичных векторов , , могут быть выражены через угловые элементы Ω, ω и i орбиты ККМ следующим образом:

Пусть I, - наклонение и долгота восходящего узла, и - широта в орбите возмущающего тела относительно базовой геоцентрической экваториальной системы координат XYZ, а i, Ω' и u' - аналогичные элементы орбиты того же тела относительно орбитальной системы координат ξηζ; при этом Ω' отсчитывается в плоскости ξη орбиты ККМ от направления на перицентр π орбиты ККМ (см. фигура 1).

Тогда для координат единичного вектора , направленного в точку S, где в текущий момент времени находится третье тело, будут справедливы представления:

,

,

,

откуда, на основании (3) и с учетом (4), могут быть получены следующие соотношения для α, β, γ:

За счет возмущающего гравитационного притяжения со стороны третьего тела, элементы орбиты ККМ будут со временем изменяться. Эти изменения для оскулирующих элементов {a, e, i, Ω, ω, M}, обусловленные влиянием возмущающей функции (2), могут быть описаны с помощью уравнений Лагранжа [Д6].

Выполним осреднение возмущающей функции R от третьего тела за один оборот ККМ по своей орбите в соответствии со схемой:

где М - средняя аномалия ККМ при его движении по орбите.

В результате осреднения получим следующее выражение для , определяющее его зависимость от элементов а и е орбиты ККМ, расстояния до третьего тела r' и направляющих косинусов α и β:

Если обозначить через осредненные за виток элементы орбиты КА по схеме, аналогичной (6), то для указанных элементов будут справедливы следующие осредненные уравнения Лагранжа:

Легко установить, что в результате осреднения будет иметь место .

Поскольку согласно (5) направляющие косинусы α и β зависят только от параметров i', Ω' и u' траектории третьего тела относительно орбитальной системы координат ξηζ, то для расчета частных производных от по параметрам i, Ω, ω орбиты ККМ необходимо знать зависимость между угловыми параметрами орбиты ККМ и траектории возмущающего тела. На основании решения сферического треугольника из рисунка 1 можно установить следующие зависимости:

Если предположить, что наклон орбиты возмущающего тела и долгота ее восходящего узла в базовой системе координат XYZ не меняется за оборот ККМ по своей орбите, то из (9) будет следовать:

,

,

.

Тем самым установлена связь между изменениями элементов δi', δ(ω+Ω') орбиты возмущающего тела относительно орбитальной системы координат ξηζ и изменениями элементов δi, δΩ орбиты ККМ в базовой экваториальной системе координат XYZ.

Вычисляя, с учетом этих зависимостей, частные производные от по соответствующим угловым элементам орбиты ККМ, система уравнений Лагранжа (8), определяющая изменения параметров орбиты ККМ за счет притяжения третьего тела, может быть преобразована к виду:

Шаг 3: Оценка влияния сопротивления атмосферы на изменение высокоэллиптических орбит увода

Сила аэродинамического сопротивления верхних слоев атмосферы, оказывающая тормозящее воздействие на движение ККМ, влияет на изменение практически всех элементов орбиты ККМ, находящегося в зоне ее действия. Однако наиболее заметно за счет сопротивления атмосферы изменяются большая полуось и эксцентриситет орбиты.

Для орбит увода из области ГСО с большим эксцентриситетом влияние сопротивления атмосферы будет проявляться только на достаточно коротких участках полета ККМ в некоторой окрестности перицентра. Интегральный эффект сопротивления атмосферы за виток для таких орбит может быть представлен в виде определенного импульса скорости ΔV, прикладываемого в направлении, противоположном движению ККМ, в перицентре его орбиты. В этом случае произойдет изменение большой полуоси орбиты на величину Δa, так что

где V_π - скорость ККМ в перицентре орбиты, μ_З - гравитационная постоянная Земли. Однако, при этом, перицентральное расстояние орбиты r_π=a(1-e) останется практически неизменным.

Изменение (уменьшение) большой полуоси на величину Δa при неизменном r_π повлечет за собой изменение эксцентриситета согласно формульной зависимости:

Поскольку Δa имеет отрицательный знак, то из (12) следует, что Δe также будет иметь отрицательное значение, т.е. эксцентриситет орбиты уменьшится.

Уменьшение большой полуоси и эксцентриситета приведет к уменьшению и апоцентрального расстояния орбиты r_α, оно станет таким: r_α=(a+Δa)[1+(e+Δe)]. Подобное изменение r_α на каждом витке (а вместе с ним и соответствующее уменьшение высоты апоцентра H_α) при низком перицентре орбиты и его длительном нахождении в зоне действия атмосферы может привести в пределе к скруглению орбиты.

Шаг 4: Оценка времени существования ККМ на орбитах увода из области ГСО

Для баллистического существования ККМ на околоземной орбите важным является значение параметра H_π, характеризующего минимальную высоту этой орбиты над поверхностью Земли, зависящего от большой полуоси а и эксцентриситета е орбиты:

Н_π=a(1-e)-r_e

где r_e - средний радиус Земли.

Нетрудно установить зависимость изменения δH_π параметра H_π от изменения большой полуоси - δa и эксцентриситета - δe орбиты ККМ:

Переводимый из области ГСО на орбиту увода отработавший объект ККМ будет существовать в космосе как угодно долго, если даже с учетом эволюции этой орбиты за счет влияния возмущающих факторов величина параметра H_π не достигнет критического предела. Принято считать (и это подтверждается практикой сопровождения многочисленных сходящих с орбиты ККМ), что таким пределом является достижение параметром H_π значений H_π<80 км, когда ККМ уже входит в плотные слои атмосферы, дальнейший полет его по орбите становится невозможным и ККМ падает на Землю.

Если же ставится задача выбора таких орбит увода, на которых удаляемый из области ГСО отработавший крупноразмерный объект космической техники будет иметь ограниченное время существования, что соответствует международным принципам по ограничению техногенного засорения околоземного космического пространства в целях его безопасного использования, то необходимо ответить на вопрос, возможно ли достижение перицентром значений H_π≤80 км в результате эволюции выбираемых орбит.

Шаг 5: Установление зависимости времени существования ККМ на орбитах увода от начальных параметров и условий движения по этим орбитам

Как было установлено выше, возмущения гравитационной природы - от нецентрального гравитационного поля Земли, а также со стороны Луны Солнца - не приводят к вековым и долгопериодическим изменениям большой полуоси орбит ИСЗ, в частности, орбит увода из области ГСО.

В то же время такие возмущения могут стать причиной изменения эксцентриситетов орбит в пределах достаточно длительных периодов времени. В результате выполненных оценок и сравнений было установлено, что наиболее сильное влияние на изменение эксцентриситетов высокоэллиптических орбит ИСЗ оказывает притяжение третьих тел - Луны и Солнца. В этом случае, согласно уравнениям (10), изменение осредненного за виток эксцентриситета орбиты определяется зависимостью:

где α, β - проекции единичного вектора, направленного из центра Земли на возмущающее тело, на оси ξ, η орбитальной системы координат . ξηζ

Величины α, β изменяются вместе с движением возмущающего тела вокруг Земли, а также в результате прецессионного движения плоскости ξη орбитальной системы координат и ее осей за счет влияния нецентральной части геопотенциала, что приводит к изменению параметров ω, Ω, i орбиты ККМ, а вместе с ними и α, β согласно формулам (3-5). Используя данные зависимости можно установить, что

Из формулы (14) следует, что эксцентриситет орбиты ККМ будет уменьшаться, а высота перигея орбиты Н_π, согласно (13), будет соответственно возрастать, когда α и β имеют одинаковый знак. Это будет происходить тогда, когда проекция направления на возмущающее тело на плоскость ξη орбитальной системы координат находится в первом или третьем квадранте этой плоскости (заштрихованные зоны на фигуре 2).

Все будет происходить наоборот (эксцентриситет увеличиваться, а Н_π уменьшаться) при нахождении проекции направления на возмущающее тело во втором или четвертом квадранте базовой плоскости ξη, когда α и β имеют разные знаки. В тех случаях, когда проекция направления на возмущающее тело находится на одной из осей ξ или η, т.е. когда α или β равно нулю, изменения эксцентриситета не происходит.

При движении возмущающего тела по своей траектории его проекция на плоскость ξη орбиты ККМ будет переходить из одного квадранта этой плоскости в другую, что будет приводить к уменьшению или увеличению эксцентриситета орбиты. При этом, чем медленнее будет происходить переход возмущающего тела из одной зоны изменения эксцентриситета в другую, тем дольше будет сохраняться тенденция на увеличение или уменьшение эксцентриситета, приводящая к увеличению времени, в течение которого будет происходить уменьшение или увеличение высоты Н_π, влияющей, в конечном счете, на время баллистического существования ККМ в космосе.

Более полная и точная качественная оценка изменений эксцентриситета и высоты Н_π конкретных орбит увода из области ГСО за определенное время может быть получена в результате интегрирования уравнения (14), в которых произведение αβ представлено в виде (15). При интегрировании данного уравнения могут быть использованы исходные значения большой полуоси а (входит в n посредством зависимости ) и эксцентриситета е рассматриваемой орбиты увода; а также угловые элементы i, Ω, ω той же орбиты. При этом следует учитывать вековые изменения параметров Ω, ω согласно зависимостям (1). Соответствующие значения элементов i', Ω' траектории третьего тела, и его широты u' относительно орбитальной системы координат , ξηζ могут быть получены на основании соотношений (9), а также следующих зависимостей:

,

.

Следует отметить, что в результате выполненного детального анализа было установлено, что изменение эксцентриситетов эллиптических орбит увода из области ГСО на достаточно длительных интервалах времени за счет влияния Солнца примерно на порядок больше, чем за счет притяжения Луны. Поэтому для получения искомой качественной оценки изменения эксцентриситетов конкретных орбит увода достаточно будет учитывать в качестве возмущающего третьего тела только Солнце.

В этом случае можно принять, что наклонение орбиты Солнца (эклиптики) к экватору Земли I=23°.43472, а долгота восходящего узла этой орбиты . Для расчета широты Солнца относительно базовой геоцентрической экваториальной системы координат на заданный момент времени t можно воспользоваться соотношением:

, где t₀ - время ближайшего к t момента весеннего равноденствия (обычно оно приходится на 20-21 марта каждого года).

Для получения точных оценок по эволюции орбит увода, на которых остаются РБ, обеспечившие выведение КА на ГСО, в зависимости от исходных параметров этих орбит и начала движен