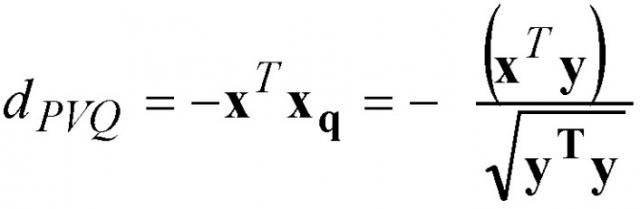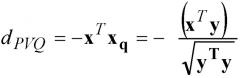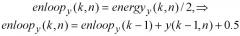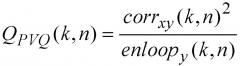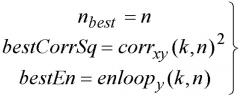Поиск формы пирамидального векторного квантователя

Поиск формы пирамидального векторного квантователя

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ

Раскрытие данной заявки, в общем, относится к векторному квантованию (VQ), выполняемому кодером.

УРОВЕНЬ ТЕХНИКИ

Является известным, что неограниченное векторное квантование является оптимальным способом квантования для сгруппированных отсчетов, то есть, векторов, некоторой длины. Однако осуществление неограниченного векторного квантования имеет следствием высокие требования с точки зрения сложности и емкости памяти. Желание обеспечить возможность осуществления векторного квантования также в ситуациях с ограничениями на память и сложность поиска, привело к разработке так называемых структурированных векторных квантователей. Разные структуры дают разные компромиссные соотношения с точки зрения сложности поиска и требований к памяти. Один такой способ является так называемым векторным квантованием усиления-формы, где целевой вектор t представляется с использованием вектора формы x и значения усиления G:

(Уравнение 0)

Концепция векторного квантования усиления-формы состоит в том, чтобы квантовать пару {x, G} вместо непосредственного квантования целевого вектора t. Компоненты усиления (G) и формы (x) кодируются с использованием квантователя формы, который настроен для нормализованного ввода формы, и квантователя усиления, который управляет динамикой сигнала. Эта структура усиления-формы часто используется в кодировании аудио, так как разделение на динамику и форму, также упоминаемое как тонкая структура, хорошо соответствует перцепционной слуховой модели. Концепция усиления-формы также может применяться к коэффициентам дискретного косинусного преобразования или другим коэффициентам, используемым в кодировании видео.

Много кодеков речи и аудио, таких как ITU-T G.718 и IETF Opus (RFC 6716), используют VQ усиления-формы на основе структурированного PVQ, чтобы кодировать спектральные коэффициенты целевого сигнала речи/аудио.

Концепция кодирования PVQ была введена Р. Фишером (R. Fischer) во временном промежутке 1983-1986 и с того времени развилась до практического использования с появлением более эффективных цифровых сигнальных процессоров, DSP. Концепция кодирования PVQ включает в себя поиск, определение местоположения и затем кодирование точки на N-мерной гиперпирамиде с целочисленной L1-нормой K единичных импульсов. Так называемая L1-норма является суммой абсолютных значений вектора, то есть, абсолютная сумма вектора PVQ из целых чисел со знаком ограничивается, чтобы быть в точности K, где единичный импульс представляется посредством целочисленного значения, равного "1". Целое число со знаком обеспечивает возможность представления отрицательных целых чисел, по отношению к беззнаковому, которое может представлять только неотрицательные целые числа.

Одно из интересных преимуществ в связи с подходом кодирования на основе структурированного PVQ в отличие от многих других структурированных квантований VQ состоит в том, что не имеется никакого связанного предела в отношении размерности N, таким образом, способы поиска, разработанные для кодирования PVQ, должны быть применимы к любой размерности N и к любому значению K.

Одна проблема с квантованием формы структурированного PVQ состоит в том, чтобы находить наилучший возможный квантованный вектор с использованием разумной величины сложности. Для кодирования речи и аудио более высокой скорости, когда количество разрешенных единичных импульсов K, может становиться очень большим и размерность N также может быть большой, имеются даже более сильные потребности, чтобы иметь эффективный поиск PVQ при поддержании качества, например, с точки зрения отношения сигнала к шуму, SNR, восстановленной речи/аудио.

Дополнительно, использование концепции PVQ не ограничено областью кодирования речи и аудио. В текущее время, так называемый Инженерный совет Интернета, IETF, занимается разработкой видеокодека, где коэффициенты дискретного косинусного преобразования, DCT, кодируются с использованием основанного на PVQ алгоритма. В кодировании видео является даже более важным, чем в кодировании аудио, иметь процедуру эффективного поиска, так как количество коэффициентов может становиться очень большим с большими устройствами отображения.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Для структурированного PVQ является желательным обеспечить возможность вычислительно эффективного поиска формы, который все еще обеспечивает высокое отношение сигнала к шуму. Особенно для осуществлений, включающих в себя DSP с фиксированной точностью. Решение, обеспеченное здесь, обеспечивает возможность вычислительно эффективного поиска формы PVQ, посредством обеспечения улучшенного точного поиска PVQ.

Согласно первому аспекту, обеспечивается способ для поиска формы PVQ, подлежащий выполнению посредством кодера. Предполагается, что PVQ включает в себя взятие целевого вектора x в качестве ввода, вывод вектора y посредством итеративного добавления единичных импульсов во внутреннем цикле поиска по размерности. Обеспеченный способ содержит, до входа в следующий внутренний цикл поиска по размерности для добавления единичного импульса: определение, на основе максимальной амплитуды импульса, maxamp_y, текущего вектора y, того, необходима ли большая, чем текущая битовая длина слова, чтобы представлять, способом без потерь, переменную, enloop_y. Переменная enloop_y относится к накопленной энергии y, в наступающем внутреннем цикле по размерности.

Согласно второму аспекту, обеспечивается кодер, для поиска формы PVQ. Предполагается, что PVQ включает в себя взятие целевого вектора x в качестве ввода, вывод вектора y посредством итеративного добавления единичных импульсов во внутреннем цикле поиска по размерности. Обеспеченный кодер сконфигурирован с возможностью, до входа в следующий внутренний цикл поиска по размерности для добавления единичного импульса: определять, на основе максимальной амплитуды импульса, maxamp_y, текущего вектора y, то, необходима ли большая, чем текущая битовая длина слова, чтобы представлять, способом без потерь, переменную, enloop_y. Переменная enloop_y относится к накопленной энергии y, в наступающем внутреннем цикле по размерности.

Способ может содержать и кодер может быть сконфигурирован с возможностью, до входа в следующий внутренний цикл по размерности для добавления единичного импульса: определение, на основе максимального абсолютного значения, xabs_max, входного вектора, x, возможного сдвига вверх, в битовом слове, накопленного значения корреляции внутри цикла следующего цикла, corr_xy, между x и вектором y.

Способ может содержать и кодер может быть сконфигурирован с возможностью, когда необходима большая, чем текущая битовая длина слова, чтобы представлять enloop_y, выполнять вычисления внутреннего цикла с использованием более длинной битовой длины слова, чтобы представлять enloop_y.

Способ может содержать и кодер может быть сконфигурирован с возможностью, когда необходима большая, чем текущая битовая длина слова, чтобы представлять enloop_y, выполнять вычисления внутреннего цикла с использованием более длинной битовой длины слова, чтобы представлять возведенное в квадрат накопленное значение корреляции внутри цикла, corr_xy², между x и вектором y, во внутреннем цикле.

Способ может дополнительно содержать и кодер может быть сконфигурирован с возможностью, когда отсутствует необходимость большей, чем текущая битовая длина слова, чтобы представлять enloop_y:

- выполнение вычислений внутреннего цикла посредством использования первого цикла добавления единичного импульса с использованием первой битовой длины слова, чтобы представлять enloop_y, и:

когда необходима большая, чем текущая битовая длина слова, чтобы представлять enloop_y:

- выполнение вычислений внутреннего цикла посредством использования второго цикла добавления единичного импульса с использованием более длинной битовой длины слова, чтобы представлять enloop_y, нежели первого цикла добавления единичного импульса.

Определение, на основе maxamp_y, того, необходима ли большая, чем текущая битовая длина слова, чтобы представлять enloop_y, может содержать определение характеристик случая, когда, в наступающем внутреннем цикле поиска, единичный импульс добавляется к положению в y, которое ассоциировано с maxamp_y.

Способ может дополнительно содержать и кодер может быть сконфигурирован с возможностью, во внутреннем цикле поиска по размерности для добавления единичного импульса:

- определение положения, n_best, в y для добавления единичного импульса посредством расчета перекрестного умножения, для каждого положения n в y, корреляции и значения энергии для текущего n; и возведенной в квадрат корреляции, BestCorrSq и значения энергии, bestEn, сохраненных из предыдущих значений n, как:

corr_xy² * bestEn > BestCorrSq * enloop_y,

где

, когда corr_xy² * bestEn > BestCorrSq * enloop_y

Способ также может содержать и кодер быть сконфигурирован с возможностью отслеживать maxamp_y, когда окончательное значение K, ассоциированное с целевым вектором x, превосходит пороговое значение. Здесь способ может содержать и кодер может быть сконфигурирован с возможностью вычислять запас по энергии, en_margin, только если текущее значение K превосходит пороговое значение, которое может быть пороговым значением, упомянутым в предшествующем предложении.

Согласно третьему аспекту, обеспечивается устройство связи, которое содержит кодер согласно второму аспекту.

Согласно четвертому аспекту, обеспечивается компьютерная программа, которая содержит инструкции, которые, когда исполняются на, по меньшей мере, одном процессоре, таком как DSP, предписывают упомянутому, по меньшей мере, одному процессору выполнять способ согласно первому аспекту.

Согласно пятому аспекту, обеспечивается носитель, содержащий компьютерную программу согласно четвертому аспекту, при этом носитель является одним из электронного сигнала, оптического сигнала, радиосигнала, или считываемого компьютером запоминающего носителя.

Согласно шестому аспекту, и обеспечивается кодер, который сконфигурирован с возможностью для поиска формы PVQ; PVQ берет целевой вектор x в качестве ввода и выводит вектор y посредством итеративного добавления единичных импульсов во внутреннем цикле поиска по размерности. Обеспеченный кодер содержит первый блок определения для, до входа в следующий внутренний цикл поиска по размерности для добавления единичного импульса, определения, на основе максимальной амплитуды импульса, maxamp_y, текущего вектора y, того, необходима ли большая, чем текущая битовая длина слова, чтобы представлять, способом без потерь, переменную, enloop_y, относящуюся к накопленной энергии y, в наступающем внутреннем цикле по размерности.

Кодер согласно шестому аспекту может содержать второй блок определения для, до входа в следующий внутренний цикл по размерности для добавления единичного импульса, определения, на основе максимального абсолютного значения, xabs_max, входного вектора, x, возможного сдвига вверх, в битовом слове, накопленного значения корреляции внутри цикла следующего цикла, corr_xy, между x и вектором y.

Кодер согласно шестому аспекту может содержать блок точного поиска для выполнения вычислений внутреннего цикла с использованием более длинной битовой длины слова, чтобы представлять enloop_y, когда необходима большая, чем текущая битовая длина слова, чтобы представлять enloop_y.

Кодер согласно шестому аспекту может содержать блок точного поиска для:

- выполнения вычислений внутреннего цикла посредством использования первого цикла добавления единичного импульса с использованием первой битовой длины слова, когда отсутствует необходимость большей, чем текущая битовая длина слова, чтобы представлять enloop_y, и:

- выполнения вычислений внутреннего цикла посредством использования второго цикла добавления единичного импульса с использованием более длинной битовой длины слова, нежели первого цикла добавления единичного импульса, когда необходима большая, чем текущая битовая длина слова, чтобы представлять enloop_y.

Кодер согласно шестому аспекту может содержать блок точного поиска для

- выполнения вычислений внутреннего цикла посредством использования первого цикла добавления единичного импульса, имеющего некоторую точность, когда отсутствует необходимость большей, чем текущая битовая длина слова, чтобы представлять enloop_y; и

- выполнения вычислений внутреннего цикла посредством использования второго цикла добавления единичного импульса, имеющего более высокую точность, нежели первого цикла добавления единичного импульса, когда необходима большая, чем текущая битовая длина слова, чтобы представлять enloop_y.

Кодер согласно шестому аспекту может быть сконфигурирован с возможностью выполнять определение, на основе maxamp_y, того, необходима ли большая, чем текущая битовая длина слова, чтобы представлять enloop_y, посредством определения характеристик случая, когда, в наступающем внутреннем цикле поиска, единичный импульс добавляется к положению в y, которое ассоциировано с maxamp_y.

Кодер согласно шестому аспекту может содержать блок точного поиска для, во внутреннем цикле поиска по размерности для добавления единичного импульса:

- определения положения, n_best, в y для добавления единичного импульса посредством расчета перекрестного умножения, для каждого положения n в y, корреляции и значения энергии для текущего n; и корреляции, BestCorrSq, и значения энергии, bestEn, сохраненных из предыдущих значений n, как:

corr_xy² * bestEn > BestCorrSq * enloop_y,

где

, когда corr_xy² * bestEn > BestCorrSq * enloop_y

Кодер согласно шестому аспекту может содержать блок хранения для отслеживания maxamp_y, когда количество окончательных единичных импульсов, K, ассоциированное с целевым вектором x, превосходит пороговое значение.

Согласно седьмому аспекту, обеспечивается устройство связи, которое содержит кодер согласно шестому аспекту.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Вышеупомянутые и другие цели, признаки, и преимущества технологии, здесь раскрытой, должны быть ясны из последующего более конкретного описания вариантов осуществления, как проиллюстрировано на сопровождающих чертежах. Чертежи не обязательно представлены в масштабе, акцент вместо этого делается на иллюстрации принципов технологии, здесь раскрытой.

Фиг. 1-4 иллюстрируют способ для поиска формы PVQ (точного поиска), согласно разным иллюстративным вариантам осуществления.

Фиг. 5 показывает этапы одного варианта осуществления поиска формы PVQ (точного поиска), согласно одному иллюстративному варианту осуществления.

Фиг. 6 показывает этапы поиска формы PVQ (точного поиска) из фиг. 5 более подробно, согласно одному иллюстративному варианту осуществления.

Фиг. 7 иллюстрирует варианты осуществления поиска формы PVQ.

Фиг. 8 показывает один вариант осуществления устройства связи, оснащенного кодером EVS.

Фиг. 9 показывает один вариант осуществления устройства связи, и

Фиг. 10 также показывает один вариант осуществления устройства связи.

Фиг. 11a-c показывают кодер согласно иллюстративным вариантам осуществления.

Фиг. 12 показывает пример системы кодирования аудио PVQ, где, по меньшей мере, одна часть системы содержится в кодере и/или кодеке, который в свою очередь содержится в устройстве связи, таком как мобильный телефон.

ПОДРОБНОЕ ОПИСАНИЕ

В арифметике с плавающей точкой не имеется никакой большой проблемы, относящейся к установке динамики параметров итераций поиска формы PVQ внутреннего цикла, однако, в процессорах DSP с фиксированной точностью с, например, ограниченными 16/32 битами накапливающими сумматорами (регистром, в котором сохраняются промежуточные арифметические и/или логические результаты) и переменными, является очень важным использовать способы эффективного поиска, где максимизируется ограниченный динамический диапазон переменных DSP и максимизируется точность, наряду с тем, что имеется возможность использовать столько из доступных быстрых операций процессора DSP ограниченного динамического диапазона, сколько возможно.

Признак "точность" выше указывает на возможность представлять настолько малые числа, насколько возможно, то есть, количество бит после десятичной точки для конкретной длины слова. Другой способ сформулировать это состоит в том, что точность соответствует разрешению представления, что снова определяется посредством количества десятичных или двоичных цифр. Причина для того, что может говориться, что точность в вариантах осуществления, описанных ниже, коррелирует с количеством бит после десятичной точки и не обязательно с самой длиной слова, состоит в том, что в арифметике с фиксированной точкой, могут иметься разные точности для одной и той же длины слова. Например, форматы данных 1Q15 и 2Q14 оба имеют длину слова 16, но первый формат имеет 15 бит после десятичной точки и другой 14 бит. Наименьшее представимое число будет тогда 2^-15 и 2^-14 соответственно.

Способ выполнения пирамидального векторного квантования формы раскрыт в разделе 3.2 в Valin и др., "A full-bandwidth audio codec with low complexity and very low delay", EUSIPCO, 2009. В этом документе представлен кодек MDCT, где подробности, то есть, форма, в каждом диапазоне квантуются алгебраически с использованием сферической кодовой книги и где назначение битов выводится из информации, совместно используемой между кодером и декодером. Аспекты и варианты осуществления раскрытия этой заявки, по меньшей мере, в широком смысле относятся к тому, как осуществлять поиск согласно уравнениям 4-7 в Valin и др., эффективным способом в арифметике с фиксированной точкой, ограниченной, например, 16/32 битами, вместо плавающих значений как в Valin и др.

В некоторых аспектах и вариантах осуществления, раскрытых в дальнейшем, при заданном целевом векторе x(n) (t в Уравнении 0) некоторой размерности N, и заданном некотором количестве единичных импульсов K, форма анализируется и определяется подходящий вектор восстановления x_q(n)=func(y(n)), который минимизирует ошибку квантования формы, и, таким образом, максимизирует воспринимаемое качество, например, в случае кодирования аудио. По меньшей мере, некоторые из аспектов и вариантов осуществления осуществляются, как имеющие целью нахождение оптимальной совокупности K единичных импульсов, в векторе y(n), который должен подчиняться L1 норме, при удержании сложности под управлением, то есть, настолько низкой, насколько практически возможно.

Вместо использования способов разомкнутого контура предшествующего уровня техники, чтобы определять приблизительные значения для динамического диапазона внутреннего цикла и точности накапливающего сумматора, некоторые из аспектов и вариантов осуществления конструируются, чтобы использовать низкую стоимость, с точки зрения необходимых процессорных циклов DSP и с точки зрения дополнительной необходимой программной постоянной памяти (ROM), "почти оптимальный" предварительный анализ числителя наихудшего случая и/или знаменателя наихудшего случая до начала дорогостоящих расчетов отношения искажения формы PVQ в самом внутреннем цикле поиска. "Почти оптимальный" предварительный анализ не нацелен на то, чтобы масштабировать значения на точный оптимальный максимальный динамический диапазон, но вместо этого предварительный анализ определяет почти оптимальный коэффициент масштаба степени 2, так как масштабирование степени 2 может осуществляться как сдвиги двоичного числа и такие сдвиги имеют низкую стоимость в процессорных циклах DSP и в DSP ROM.

Выбор точности знаменателя является перцепционно мотивированным, так как спектрально пиковым областям будет назначаться большая точность, чем более плоским областям.

В то время как некоторые из основных концепций, описанных в этом раскрытии, охватывают различные модификации и альтернативные конструкции, варианты осуществления аспектов показаны на чертежах и в иллюстративном коде и будут в дальнейшем описываться подробно.

ВВЕДЕНИЕ В ОБЩУЮ ОПТИМИЗАЦИЮ ПОИСКА PVQ

Квантователь структурированного PVQ на основе L1-нормы обеспечивает возможность нескольких оптимизаций поиска, где первичная оптимизация состоит в том, чтобы перемещать цель во весь положительный "квадрант" (также может упоминаться как ортант или гипероктант) в N-мерном пространстве, и вторая оптимизация состоит в том, чтобы использовать проекцию в L1-норме в качестве начального приближения для y(n). L1-норма K для PVQ(N,K) означает, что абсолютная сумма всех элементов в векторе PVQ y(n) должна быть K, в точности как абсолютная сумма всех элементов в целевом векторе формы x(n).

Третья оптимизация состоит в том, чтобы итеративно обновлять члены отношения Q_PVQ corr_xy² и energy_y, вместо повторного вычисления Уравнения 4 (ниже) над всем векторным пространством N, для каждого изменения кандидата для вектора y(n) в поиске достижения L1-нормы K, что требуется для последующего этапа индексирования.

Вышеуказанные три главные этапа оптимизации являются оптимизациями, которые, в общем, могут существовать в прошлых вариантах реализации PVQ, таких как CELT и IETF-Opus, и частично в G.718, однако, для полноты описания аспектов и вариантов осуществления, эти этапы также кратко очерчиваются ниже.

ЭФФЕКТИВНЫЙ ПОИСК ФОРМЫ ВЕКТОРА PVQ

Обзор системы кодирования и декодирования аудио, применяющей один вариант осуществления здесь предложенного поиска формы PVQ, можно видеть на фиг. 12. Общий поиск формы с использованием пирамидальной проекции, за которой следует последовательность операций точного поиска (формы), можно видеть, например, на фиг. 5. Другой вариант осуществления части точного поиска в поиске формы изображен на фиг. 6. Поиск формы PVQ может содержать пирамидальную проекцию и точный поиск. Когда никакая пирамидальная проекция не применяется, поиск формы содержит только точный поиск. Поэтому, "точный поиск" и "поиск формы" могут иногда использоваться здесь взаимозаменяемо, так как точный поиск является частью поиска формы, и, когда не имеется никакого начального грубого поиска, посредством пирамидальной проекции, выполнение поиска формы является даже таким же, что и выполнение точного поиска. Другими словами, точный поиск может иногда быть или составлять поиск формы, и когда применяется пирамидальная проекция, точный поиск является частью поиска формы.

ВВЕДЕНИЕ В ПОИСК PVQ

Цель процедуры поиска PVQ(N,K) состоит в том, чтобы найти наилучший масштабированный и нормализованный выходной вектор x_q(n). x_q(n) определяется как:

(Уравнение 1)

Где y=y_N,K является точкой на поверхности N-мерной гиперпирамиды и L1 норма y_N,K равняется K. Другими словами, y_N,K является выбранным целочисленным вектором кода формы размера N, также упоминаемого как размерность N, согласно:

(Уравнение 2)

То есть, вектор x_q является нормализованным целочисленным подвектором единичной энергии . Наилучший вектор y является вектором, минимизирующим среднеквадратическую ошибку формы между целевым вектором x(n) и масштабированным нормализованным квантованным выходным вектором x_q. Это достигается посредством минимизации следующего искажения поиска:

(Уравнение 3)

Или эквивалентно, посредством возведения в квадрат числителя и знаменателя, максимизируя отношение Q_PVQ:

(Уравнение 4)

где corr_xy является корреляцией между x и y. В поиске оптимальной формы вектора PVQ y(n) с L1-нормой K, осуществляются итеративные обновления переменных Q_PVQ во всем положительном "квадранте" в N-мерном пространстве согласно:

(Уравнение 5)

(Уравнение 6)

где corr_xy(k-1) обозначает корреляцию, достигнутую до сих пор посредством помещения предыдущих k-1 единичных импульсов, и energy_y(k-1) обозначает накопленную энергию, достигнутую до сих пор посредством помещения предыдущих k-1 единичных импульсов, и y(k-1, n) обозначает амплитуду y в положении n от предыдущего помещения k-1 единичных импульсов. Чтобы дополнительно ускорять итеративную обработку внутри цикла для члена энергии energy_y(k) уменьшается масштаб посредством 2, таким образом, устраняя одно умножение во внутреннем цикле.

(Уравнение 7)

где enloop_y(k,n) является предпочтительной переменной энергии, используемой и накапливаемой внутри самого внутреннего цикла поиска единичного импульса, так как ее итеративное обновление требует на одно умножение меньше, чем energy_y(k,n).

(Уравнение 8)

Наилучшее положение n_best для k-ого единичного импульса, итеративно обновляется посредством увеличения n от 0 до N-1:

, если (Уравнение 9)

Чтобы избегать дорогостоящих делений, что является особенно важным в арифметике с фиксированной точкой, решение обновления максимизации Q_PVQ выполняется с использованием перекрестного умножения числителя сохраненной наилучшей возведенной в квадрат корреляции bestCorrSq и знаменателя сохраненной наилучшей энергии bestEn до сих пор, что может быть выражено как:

, если (Уравнение 10)

Итеративная максимизация для Q_PVQ(k, n) может начинаться с нулевого количества помещенных единичных импульсов или с некоторого адаптивного количества единичных импульсов предварительного помещения более низкой стоимости, на основе целочисленной проекции в точку ниже поверхности K-ой пирамиды, с гарантированным недоходом единичных импульсов в целевой L1 норме K.

АНАЛИЗ ПОДГОТОВКИ ПОИСКА PVQ

Вследствие структурированной природы целочисленного вектора PVQ y_N,K, где разрешены все возможные комбинации знака и является возможным кодировать все комбинации знака, при условии, что результирующий вектор подчиняется L1 норме K единичных импульсов, поиск выполняется во всем положительном первом "квадранте" (причина использования кавычек для "квадранта" состоит в том, что истинный квадрант существует, только когда N=2, и N может здесь быть больше, чем 2). Дополнительно, как понимается изобретателем, чтобы достигать настолько высокой точности насколько возможно для осуществления ограниченной точности, максимальное абсолютное значение xabs_max входного сигнала x(n) может предварительно анализироваться для будущего использования в настройке процедуры накопления корреляции внутреннего цикла.

для (Уравнение 11)

(Уравнение 12)

УПРАВЛЕНИЕ ЦЕЛЯМИ ОЧЕНЬ НИЗКОЙ ЭНЕРГИИ И ПОДВЕКТОРАМИ ОЧЕНЬ НИЗКОЙ ЭНЕРГИИ

В случае, когда входной целевой вектор (x в Уравнении 3 или t в Уравнении 0) является вектором из всех нулей и/или усиление вектора (например, G в Уравнении 0) является очень низким, поиск PVQ может пропускаться, и действительный вектор PVQ y может детерминированно создаваться посредством назначения половины K единичных импульсов первому положению

и оставшихся единичных импульсов последнему положению ().

Признак "цели очень низкой энергии" и "очень низкое усиление вектора" является в одном варианте осуществления настолько низким, как ноль, как проиллюстрировано в иллюстративном коде ANSI C, раскрытом ниже, где соответствующий код является:

IF(L_xsum == 0 || neg_gain == 0)

{ /* случай нулевого ввода или нулевого усиления */

Однако оно также может быть меньше, чем или равно эпсилон, или EPS, где EPS является наименьшим значением, которое больше, чем ноль и которое рассматривается, что может его представлять в выбранной точности. Например, при точности Q15 в 16-битном слове со знаком, усиление подвектора становится меньшим или равным EPS 1/2^15= 1/32768 (например, усиление вектора меньше или равно 0.000030517578125), и в случае точности Q12 в 16-битном слове со знаком для целевого вектора x(n), тогда "очень низкое" значение становится EPS=(1/2^12), например, сумма (abs(x(n))) меньше или равна 0.000244140625. В одном варианте осуществления арифметики DSP с фиксированной точкой с 16-битным словом, беззнаковый целочисленный формат может принимать любое целочисленное значение от 0 до 65546, тогда как целое число со знаком может принимать значение от -32768 до +32767. С использованием беззнакового дробного формата, 565536 уровней распределены равномерно между 0 и +1, тогда как в осуществлении дробного формата со знаком уровни будут, равным образом расположены между -1 и +1.

Посредством применения этого необязательного этапа, относящегося к нулевым векторам и низким значениям усиления, сложность поиска PVQ уменьшается и сложность индексирования распределяется/разделяется между индексированием кодера и деиндексированием декодера, то есть, никакая обработка не "тратится впустую" для поиска нулевого целевого вектора или очень низкого целевого вектора, для которого в любом случае осуществлялось бы масштабирование к нулю.

НЕОБЯЗАТЕЛЬНАЯ ПРОЕКЦИЯ ПРЕДВАРИТЕЛЬНОГО ПОИСКА PVQ

Если отношение плотности импульсов K/N больше, чем 0.5 единичных импульсов в расчете на коэффициент, например, коэффициент модифицированного дискретного косинусного преобразования, делается проекция низкой стоимости на K-1 подпирамиду и используется в качестве начальной точки для y. С другой стороны, если отношение плотности импульсов меньше, чем 0.5 единичных импульсов в расчете на коэффициент, итеративный поиск PVQ начинается с 0 предварительно помещенных единичных импульсов. Проекция низкой стоимости на "K-1" обычно является менее вычислительно дорогостоящей в процессорных циклах DSP, чем повторение поиска внутреннего цикла для единичного импульса K-1 раз. Однако недостаток проекции низкой стоимости состоит в том, что она вырабатывает неточный результат вследствие применения N-мерной функции floor. Результирующая L1-норма проекции низкой стоимости с использованием функции floor может обычно быть всем, чем угодно между "K-1" до грубо "K-5", то есть, для результата после проекции должен осуществляться точный поиск, чтобы достигать целевой нормы K.

Проекция низкой стоимости выполняется как:

(Уравнение 13)

для n=0,.., N-1 (Уравнение 14)

Если никакая проекция не делается, начальная точка является вектором y(n) со всеми нулями. Стоимость DSP проекции в процессорных циклах DSP находится в окрестности N(абсолютная сумма)+25(деление)+2N(умножение и функция floor) процессорных циклов.

В подготовке для точного поиска, чтобы достигать поверхности K-ой пирамиды, накопленное количество единичных импульсов pulse_tot, накопленная корреляция corr_xy(pulse_tot) и накопленная энергия energy_y(pulse_tot) для начальной точки вычисляется как:

(Уравнение 15)

(Уравнение 16)

(Уравнение 17)

(Уравнение 18)

ТОЧНЫЙ ПОИСК PVQ

Решение, здесь раскрытое, относится к точному поиску PVQ (который составляет или является частью поиска формы PVQ, как описано ранее). То, что было описано в предшествующих разделах, является главным образом PVQ предшествующего уровня техники, за исключением предварительного определения xabs_max, которое дополнительно описывается ниже. Окончательный целочисленный вектор формы y(n) размерности N должен подчиняться L1 норме K импульсов. Предполагается, что точный поиск сконфигурирован с возможностью начинаться с более низкой точки в пирамиде, то есть, ниже K-ой пирамиды, и итеративно находить свой путь к поверхности N-мерной K-ой гиперпирамиды. K-значение в точном поиске может обычно находится в диапазоне от 1 до 512 единичных импульсов.

Изобретатель понял, что чтобы удерживать сложность поиска и индексирования PVQ на разумном уровне, поиск может разделяться на две основные ветви, где одна ветвь используется, когда является известным, что представление энергии внутри цикла для y(n) будет оставаться в пределах 16-битного слова со знаком, или без знака, во время следующей итерации внутреннего цикла поиска, и другая ветвь используется, когда энергия внутри цикла может превосходить динамический диапазон 16-битного слова во время следующей итерации внутреннего цикла поиска.

ТОЧНЫЙ ПОИСК С ФИКСИРОВАННОЙ ТОЧНОСТЬЮ ДЛЯ МАЛОГО КОЛИЧЕСТВА ЕДИНИЧНЫХ ИМПУЛЬСОВ

Когда окончательное K является более низким, чем или равно порогу t_p=127 единичных импульсов, динамика energy_y(K) будет всегда оставаться в пределах 14 бит, и динамика сдвинутой вверх на 1 бит enloop_y(K) будет всегда оставаться в пределах 15 бит. Это обеспечивает возможность использования 16-битного слова со знаком для представления каждой enloop_y(k) внутри всех итераций внутреннего цикла точного поиска импульсов вплоть до k=K. Другими словами, не будет необходимости в битовой длине слова, превосходящей 16 бит, для представления energy_y(K) или enloop_y(K) в любой итерации внутреннего цикла точного поиска импульсов, когда K<127.

В случае доступности эффективных операторов DSP Multiply, MultiplyAdd (умножение с добавлением) и MultiplySubtract (умножение с вычитанием) для беззнаковых 16-битных переменных, порог может увеличиваться до t_p=255, так как тогда enloop_y(K) будет всегда оставаться в пределах беззнакового 16-битного слова. MultiplyAdd является здесь в одном варианте осуществления инструкциями умножения с добавлением или эквивалентными операциями, чтобы умножать значения данных, представляющих аудио и видео сигналы, на значения фильтра или преобразования и накапливать произведения, чтобы формировать результат. Операции MultiplySubtract являются такими же, как операции MultiplyAdd, за исключением того, что добавления заменены на вычитания.

В подготовке для следующего добавления единичного импульса, почти оп