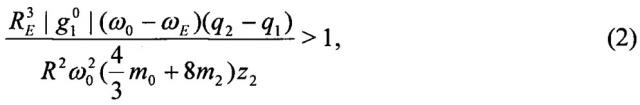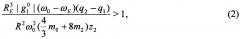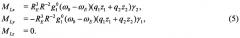Устройство стабилизации электродинамической тросовой системы для удаления космического мусора

Устройство стабилизации электродинамической тросовой системы для удаления космического мусора

Иллюстрации

Показать все

Реферат

Изобретение относится к области космической техники и может быть использовано для стабилизации космической тросовой системы в околоземном пространстве с целью повышения эффективности его функционирования в процессе уборки космического мусора.

Выполненные к настоящему времени теоретические разработки и проведенные испытания в открытом космосе позволяют утверждать, что электродинамические тросовые системы (ЭДТС), включающие проводящие тросы, взаимодействующие с магнитным полем Земли, могут использоваться как источники Амперовой силы тяги в околоземном пространстве [1]. В частности, ЭДТС может использоваться как перспективный источник силы тяги, не требующий расхода топлива, для решения актуальной задачи спуска с орбиты отработанных элементов космических систем [2-11].

Из анализа направлений тока, протекающего вдоль троса, и магнитной индукции магнитного поля Земли следует, что наибольшей эффективностью отличается трос, функционирующий в режиме проводника с током, ориентированного в околоземном пространстве вдоль местной вертикали. Данная ориентация троса является устойчивой в центральном ньютоновском гравитационном поле [1]. Вместе с тем, установлено, что под действием момента сил Ампера вертикальная ориентация троса разрушается.

В.В. Белецкий и Е.М. Левин в статье "Dynamics of Space Tether Systems," Advances in the Astronautical Sciences, v. 83, AAS, 1993 описали многочисленные моды неустойчивости ЭДТС, наблюдаемые даже на круговых экваториальных орбитах в предположении стационарности геомагнитного поля.

J. Pelaez, E.C. Lorenzini, О. Lopez-Rebollal и М. Ruiz в докладе «А new kind of dynamic instability in electrodynamic tethers», AAS 00-190, AAS/AIAA Space Flight Meeting Jan. 23-26, 2000 выявили, что неустойчивость присуща всем неуправляемым движениям ЭДТС и ее просто невозможно избежать.

R.P. Hoyt и R.L. Forward в докладе «The Terminator Tether: Autonomous Deorbit of LEO Spacecraft for Space Debris Mitigation», AIAA 00-0329, 38^th Aerospace Sciences Meeting and Exhibit, Jan. 10-13 2000, Reno, Nevada пришли к выводу о том, что для борьбы с динамической неустойчивостью должно использоваться управление.

J. Corsi и L. Iess в статье «Stability and control of electrodynamic tethers for deorbiting applications», Acta Astronautica 48 (2001) 491-501 показали, что для успешного использования ЭДТС для удаления космического мусора следует периодически выключать ток, протекающий по тросу.

Zhong R. и Zhu Z.H. в статье «Libration dynamics and stability of electrodynamic tethers in satellite deorbit», Celestial Mechanics and Dynamical Astronomy 116 (2013) 279-298 показали, что ЭДТС не может эффективно выполнять задачу увода космического мусора с орбиты в условиях неустойчивых колебаний и предложили простую стратегию управления током путем его периодического выключения.

Таким образом, проблема неустойчивости ЭДТС известна и рассматривается специалистами как критически важная [8, 12]. Решению этой проблемы посвящен ряд работ [11, 13, 14, 15]. Среди возможных подходов к ее решению предлагаются упомянутые выше варианты использования устройств для периодического выключения тока, протекающего по тросу, или переключения направления тока, а также более сложные варианты управления силой тока.

Так, Levin Е.М. и Carroll J.A. в патентах «Apparatus for observing and stabilizing electrodynamic tethers», U.S. Pat. No. 6,755,377 B1, Jun. 29, 2004. и Levin E.M., Carroll J.A. «Method for observing and stabilizing electrodynamic tethers», U.S. Pat. No. 6,758,443 B1, Jul. 6, 2004, предложили формировать управляющие сигналы на основе измерений параметров текущего состояния троса и последующих расчетов [16, 17].

Наиболее близким к заявляемому изобретению является патент [17], выбранный в качестве прототипа, предлагающий измерять напряжение и силу тока в тросе и, возможно, натяжение троса, чтобы обеспечивать такие вариации силы тока, которые совпадают со значениями силы тока, индуцированными геомагнитным полем при нежелательных компонентах скорости троса. При этом, в соответствии с алгоритмом, требуется интегрирование системы дифференциальных уравнений движения троса для выработки управляющего сигнала на формирование управляющего импульса силы тока.

Общим недостатком известных способов управления электродинамическим тросом является сложность системы управления, вызванная необходимостью выполнения измерений для оценки состояния троса в процессе движения. Кроме того, во многих случаях ЭДТС должна функционировать в условиях, предполагающих непрерывное протекание тока вдоль троса в одном направлении, например, для создания упомянутой выше силы тяги или для работы ЭДТС в режиме генератора мощности [18]. В этих случаях упомянутое управление снижает эффективность ЭДТС и ограничивает возможности их использования.

Задача изобретения заключается в расширении области применимости ЭДТС путем повышения запаса ее устойчивости в режиме функционирования в состоянии ориентации вдоль местной вертикали.

Заявленное устройство поясняется Фиг. 1-4, где на Фиг. 1 представлена орбитальная система координат Сξηζ, являющаяся базовой системой при решении задачи стабилизации электродинамического троса. Точка С является центром масс ЭДТС. В номинальном режиме ось z, направленная вдоль натянутого троса, коллинеарна оси Сζ, направленной вдоль радиуса-вектора точки С относительно притягивающего центра. Оси Сξ и Сη направлены соответственно по положительной трансверсали к орбите и по нормали к плоскости орбиты. На Фиг. 2 представлена конструктивная схема электродинамического троса, на Фиг. 3 представлена граница области существования «косых» положений равновесия электродинамического троса, на Фиг. 4 представлены результаты численного моделирования процесса стабилизации ЭДТС.

Заявленное устройство поясняется Фиг. 2, на которой 1 - коллектор положительного заряда, 2 - электроизолирующее крепление, 3 - электронный эмиттер (не менее, чем один), электрически соединенный с коллектором 1 и расположенный внутри электроизолирующего крепления 2, соединяющего коллектор 1 и концевое тело 4 троса 5, противоположный конец которого заканчивается концевым телом 6. Концевое тело 6 электрически соединено с электронным эмиттером (не менее, чем одним) 3, расположенным внутри электроизолирующего крепления 2, соединяющего концевое тело 6 троса 5 и коллектор отрицательного заряда 7.

Работа заявленного устройства поясняется Фиг. 2. К концам проводящего изолированного троса 5 (Фиг. 2) присоединены коллекторы - устройства для сбора электрических зарядов. Коллектор 1, находящийся на верхнем конце троса (том, который дальше от Земли), с помощью электроизолирующих креплений 2 соединен с концевым телом 4 проводящего троса 5. Коллектор 1 получает положительный заряд, поддерживаемый одним или несколькими электронными эмиттерами (например, полевыми электронными эмиттерами, холодными электронными эмиттерами на основе нанопористого углерода, или холловскими ионными источниками) 3, передающими отрицательный заряд на концевое тело 4. На противоположном конце троса (том, который ближе к Земле) концевое тело 6 аналогичным образом соединено с коллектором 7. Коллектор 7 получает отрицательный заряд, поддерживаемый одним или несколькими электронными эмиттерами 3, передающими отрицательный заряд с концевого тела 6.

Технический результат, достигаемый заявляемым изобретением, состоит в упрощении устройства стабилизации троса, повышении его надежности и расширении области устойчивости вертикального положения троса.

Указанный технический результат достигается тем, что размещение положительно заряженного коллектора на верхнем конце троса и отрицательно заряженного коллектора на нижнем конце троса приводит к возбуждению момента сил Лоренца, воздействующих на коллекторы, и оказывающего ориентирующее действие на трос, а выполнение условий на параметры ЭДТС обеспечивает существование и устойчивость положения равновесия, и при наличии демпфирования (обеспечиваемого каким-либо из известных способов - например, за счет тепловых потерь при протекании тока в тросе) решает задачу стабилизации троса в положении вдоль местной вертикали.

Работоспособность заявленного устройства обеспечивается источниками электроэнергии, преобразованной из световой с помощью солнечных батарей, входящих в состав ЭДТС (на Фиг. 2 не показаны ввиду их известности и широкого использования). Источники электроэнергии обеспечивают работу эмиттеров по поддержанию зарядов на коллекторах и предотвращению разрядки коллекторов в процессе движения через ионосферную плазму.

Сущность заявленного изобретения заключается в следующем. Для ЭДТС, центр масс которой (точка С) движется со скоростью v_C относительно магнитного поля Земли (МПЗ), характеризуемого магнитной индукцией В, накопление электростатических зарядов q₁ и q₂ на коллекторах ЭДТС, приводит к возникновению момента M_L лоренцевых сил, определяемого по формуле

оказывающего при определенных условиях ориентирующее воздействие на ЭДТС и используемого в качестве восстанавливающего момента наряду с гравитационным моментом.

В данном случае, тела, присоединенные к концам троса, считаются точечными, а их вращательным движением можно пренебречь ввиду малости отношения характерного размера тела к длине троса. Упругие деформации троса также не рассматриваются. Трос считается натянутым, а его либрационное движение относительно центра масс не влияет на его орбитальное движение. При сделанных предположениях , , где z₁ - расстояние от центра масс системы до центра масс устройств, присоединенных к тросу на нижнем конце, z₂ - расстояние от центра масс системы до центра масс устройств, присоединенных к тросу на верхнем конце, ω₀ - орбитальная угловая скорость центра масс ЭДТС, ω_E - угловая скорость суточного вращения Земли, R - радиус орбиты центра масс ЭДТС. В условиях моделирования МПЗ прямым магнитным диполем , где - гауссов коэффициент, R_E - средний радиус Земли.

Анализ математической модели ЭДТС позволяет получить условия, при которых достигается режим стабилизированного движения ЭДТС. Установлено (подробнее - в Приложении), что существование, единственность и устойчивость положения равновесия троса в натянутом состоянии вдоль местной вертикали обеспечивается выбором таких параметров троса и присоединенных к нему вышеописанных устройств, для которых расстояния от центра масс системы до центров заряженных коллекторов одинаковы и выполняется неравенство

где m₀ - масса троса, m₂ - масса устройств, присоединенных к тросу на верхнем конце, z₂ - расстояние от центра масс системы до центра масс устройств, присоединенных к тросу на верхнем конце.

Заявленное изобретение апробировано компьютерным моделированием на базе математико-механического факультета заявителя - Санкт-Петербургского государственного университета. Примеры апробации приведены ниже.

Пример 1. Вначале был выполнен численный анализ неравенства (2) для множества ЭДТС со следующими значениями радиуса орбиты и электростатических параметров: R=7⋅10⁶ м, q₁=-5⋅10^-2 Кл, q₂=5⋅10^-2 Кл. Результат приведен на Фиг. 3, где по горизонтальной оси отложены значения m₀/6+m₂ (в кг), а по вертикальной - значения z₂ (в м). Если длины и массы таковы, что изображающая точка лежит ниже кривой на графике, то неравенство (2) выполняется. Например, пусть z₂=100 м, z₁=-100 м, погонная масса троса γ=2⋅10^-3 кг/м, m₁=m₂=16 кг. Тогда неравенство (2) выполнено.

Пример 2. Выполнена серия численных экспериментов, моделирующих процесс стабилизации ЭДТС в режиме вертикального расположения троса. Для иллюстрации численного моделирования процесса стабилизации выбран пример конструкции ЭДТС, содержащей трос длиной 200 м, обладающий погонной массой γ=2⋅10^-3 кг/м и проводящий ток I=2А. Масса на нижнем конце троса m₁=55 кг, масса на верхнем конце троса m₂=50 кг. Центр заряда коллектора на нижнем конце троса имеет координату z₁=-95 м, центр заряда коллектора на верхнем конце троса имеет координату z₂=105 м. Центр масс ЭДТС движется по круговой экваториальной орбите радиуса R=7⋅10⁶ м. Модельный диссипативный момент пропорционален относительной угловой скорости ЭДТС М_D=-hJω₀ω' и содержит множителем безразмерный малый параметр, выбранный равным h=0.001. J - тензор инерции ЭДТС.

Фиг. 4-6 иллюстрируют движение ЭДТС с нулевыми зарядами на коллекторах (система стабилизации не работает). В начальный момент времени трос был отклонен от местной вертикали на угол 1 рад в плоскости (η, ζ) и отпущен без начальной угловой скорости относительно орбитальной системы координат. Вертикальное положение троса оказывается неустойчивым, что наглядно демонстрируется поведением направляющего косинуса γ₃ (Фиг. 4), все сильнее отклоняющегося от целевого значения γ₃=1 под действием Амперова момента, а также поведением компонент относительной угловой скорости, отнесенной к орбитальной угловой скорости (Фиг. 5). Заметим, что при этом во все время движения величина возмущающего Амперова момента остается малой (Фиг. 6) - на 2 порядка меньше величины гравитационного момента (Фиг. 7), стремящегося стабилизировать ЭДТС вдоль местной вертикали.

Фиг. 8-11 иллюстрируют движение ЭДТС с ненулевыми зарядами на коллекторах (система стабилизации работает): q1=-0.05 Кл, q2=0.05 Кл). Все остальные параметры ЭДТС и начальные условия ее движения сохранены без изменений, как в случае Фиг. 4-7, соответствующих нерабочему режиму системы стабилизации. Результаты численного интегрирования показывают, что направляющий косинус γ₃ стремится к целевому значению γ₃=1 (Фиг. 8), а компоненты относительной угловой скорости, отнесенной к орбитальной угловой скорости, стремятся к нулю (Фиг. 9). При этом диссипативный момент остается весьма малым по величине (на порядок меньше возмущающего - Амперова момента и на 3 порядка меньше гравитационного момента) во все время движения (Фиг. 10) и поэтому причине соответствующая ему кривая сливается с горизонтальной осью на Фиг. 11, где приведены модули всех действующих на ЭДТС моментов.

На всех Фиг. 4-11 по горизонтальной оси откладывается безразмерный угол - аргумент широты u=ω₀t. Заметим, что в данном примере для иллюстрации численного моделирования выбраны «худшие» значения параметров ЭДТС, для которых условие (2) не выполняется. Более того, не выполняется даже соотношение z₁=-z₂, что позволяет рассматривать Амперов момент как постоянно действующее возмущение, естественным образом возникающее в данной задаче. Сравнение графиков, приведенных на Фиг. 4 и Фиг. 8, а также Фиг. 5 и Фиг. 9, свидетельствует о том, что заявляемое устройство, технически более простое и надежное по сравнению с прототипом, заметно расширяет область устойчивости вертикального положения троса (повышает устойчивость вертикального положения троса), а следовательно, повышает работоспособность ЭДТС.

Как показали аналитические исследования, компьютерное моделирование процессов стабилизации ЭДТС в режиме вертикального расположения троса, и проведенные численные расчеты, заявленное устройство может работать в режиме отсутствия системы управления силой тока, пропускаемого по тросу, что упрощает устройство стабилизации троса и повышает его надежность. При этом заявленное устройство расширяет область устойчивости вертикального положения троса за счет эффективно реализованной возможности разделения зарядов на концах троса и использования возникающего вследствие этого момента сил Лоренца - дополнительного стабилизирующего момента. Все это позволяет эффективнее по сравнению с аналогами обеспечить номинальный режим движения ЭДТС для удаления космического мусора.

Список использованной литературы:

1. Белецкий В.В., Левин Е.М. Динамика космических тросовых систем. М., Наука, 1990, 336 с.

2. Forward R.L. Electrodynamic drag terminator tether, Appendix K of high strength-to-weight tapered Hoytether for LEO to GEO payload transport, Final Report on NASA SBIR Phase I Contract NAS8-40690, 10 July 1996.

3. Forward R.L., Hoyt R.P., Uphoff C. Application of the Terminator Tether™ electrodynamic drag technology to the deorbit of constellation spacecraft, Paper AIAA 98-3491, 34th Joint Propulsion Conference and Exhibition, Cleveland, OH, July 13-15, 1998.

4. Forward R.L., Hoyt R.P. Terminator Tether™: a spacecraft deorbit device, Journal of Spacecraft and Rockets 37 (2000) 187-196.

5. Cosmo M.L., Lorenzini E.C. (Eds.) Tethers in Space Handbook, 3-rd ed., Smithsonian Astrophysical Observatory, Cambridge, MA, USA, 1997.

6. Forward R.L. et. al. Electrodynamic tether and method of use, U.S. Pat. No. 6,116,544, Sep. 12, 2000.

7. Vannaroni G., Dobrowolny M., De Venuto F. Deorbiting with electrodynamic tethers: comparison between different tether configurations, Space Debris 1 (2001) 159-172.

8. Iess L., Bruno C. et al. Satellite de-orbiting by means of electrodynamic tethers part I: general concepts and requirements, Acta Astronautica 50 (2002) 399-406.

9. Iess L., Bruno C. et al. Satellite deorbiting by means of electrodynamic tethers Part II: system configuration and performance, Acta Astronautica 50 (2002) 407-416.

10. Ishige Y., Kawamoto S., Kibe S. Study on electrodynamic tether system for space debris removal, Acta Astronautica 55 (2004) 917-929.

11. Yamaigiwa Y., Hiragi E., Kishimoto T. Dynamic behavior of electrodynamic tether deorbit system on elliptical orbit and its control by Lorentz force, Aerospace Science and Technology 9 (2005) 366-373.

12. Zhong R., Zhu Z.H. Libration dynamics and stability of electrodynamic tethers in satellite deorbit, Celestial Mechanics and Dynamical Astronomy 116 (2013) 279-298.

13. Corsi J., Iess L. Stability and control of electrodynamic tethers for de-orbiting applications, Acta Astronautica 48 (2001) 491-501.

14. Pelaez J., Ruiz M., Lopez-Rebollal O., Lorenzini E.C., Cosmo M. A two bar model for the dynamics and stability of electrodynamic tethers, Journal of Guidance, Control and Dynamics 25 (2002) 1125-1135.

15. Larsen M.B., Blanke M. Passivity-based control of a rigid electrodynamic tether, Journal of Guidance, Control, and Dynamics 34 (2011) 118-127.

16. Levin E.M., Carroll J.A. Apparatus for observing and stabilizing electrodynamic tethers, U.S. Pat. No. 6,755,377 B1, Jun. 29, 2004.

17. Levin E.M., Carroll J.A. Method for observing and stabilizing electrodynamic tethers, U.S. Pat. No. 6,758,443 B1, Jul. 6, 2004. - прототип

18. Roberts et al. Tether power generator for Earth orbiting satellites, U.S. Pat. No. 4,923,151 B1, Mar. 1, 1998.

19. Белецкий B.B. Движение спутника относительно центра масс в гравитационном поле. М., изд. Моск. ун-та, 1975. 308 с.

20. Петров К.Г., Тихонов А.А. Момент сил Лоренца, действующих на заряженный спутник в магнитном поле Земли. Ч.2: Вычисление момента и оценки его составляющих // Вестн. С.-Петербург. ун-та. Сер. 1. 1999. Вып. 3 (No. 15). С. 81-91.

ПРИЛОЖЕНИЕ

к заявке на выдачу патента РФ на изобретение «Устройство стабилизации электродинамической тросовой системы для удаления космического мусора»

Ниже приведены пояснения к тексту описания со ссылкой на источники информации с сохранением порядка их нумерации, приведенные в тексте описания, и на рисунки.

На протяжении последних 50 лет космические тросовые системы (КТС) неуклонно привлекают внимание исследователей, изучающих динамику КТС в околоземном пространстве, как аналитическими методами, так и с помощью экспериментов в околоземном пространстве. Еще в начале 60-х годов XX века, после успешной реализации технических решений, разработанных для спутника Transit-1В и экспериментов по движению космических аппаратов Gemini-11 и Gemini-12 в режиме космической связки со ступенями ракет-носителей, стало ясно, что КТС открывают новые возможности для выполнения различных операций в космосе благодаря своим механическим свойствам [1].

С 1980-х годов XX века ведутся разработки и осуществляются испытания электродинамических тросовых систем (ЭДТС), включающие проводящие тросы, взаимодействующие с магнитным полем Земли. В этих системах тросы являются источниками не только сил натяжения, что позволяет им выполнять роль связей, но и амперовых сил, возникающих в результате электромагнитного взаимодействия протекающего по тросу тока с геомагнитным полем и оказывающих влияние на движение ЭДТС относительно магнитного поля Земли. Последнее обстоятельство позволяет рассматривать электродинамический трос как источник сил тяги в околоземном пространстве. С 1996 года электродинамический трос рассматривается многими исследователями как перспективный источник сил тяги, не требующий расхода топлива, для решения актуальной задачи спуска с орбиты отработанных элементов космических систем [2, 3, 4]. Несмотря на небольшое число экспериментов, выполненных в околоземном пространстве [5], решение задачи удаления космического мусора с орбиты с помощью ЭДТС представляется вполне возможным [6, 7, 8, 9, 10, 11].

При этом наибольшей эффективностью отличается проводящий трос, функционирующий в режиме проводника с током, ориентированного в околоземном пространстве по местной вертикали. Данная ориентация троса является устойчивой в центральном ньютоновском гравитационном поле [1]. Вместе с тем, установлено, что под действием момента сил Ампера вертикальная ориентация троса разрушается. Проблема неустойчивости ЭДТС известна и рассматривается как критически важная [8, 12]. Решению этой проблемы посвящен ряд работ [11, 13, 14, 15]. Среди возможных подходов к ее решению предлагается использовать управление силой тока, протекающего по тросу [13, 16, 17].

Поскольку в большинстве космических миссий электродинамические тросы должны быть ориентированы в околоземном пространстве в направлении местной вертикали на долговременной основе [16, 17], то проблема стабилизации электродинамического троса в указанном положении является актуальной.

Известны способы управления ориентацией электродинамического троса путем использования устройств для периодического выключения тока, протекающего по тросу, или переключения направления тока [13, 16, 17].

Для определения условий, при которых достигается режим стабилизированного движения ЭДТС, рассмотрим ЭДТС (к стр. 3, 3-й абзац сверху текса описания заявленного изобретения), центр масс которой движется по круговой кеплеровой экваториальной орбите в гравитационном и магнитном полях Земли и функционирующую в режиме, близком к состоянию обычного тяжелого троса, находящегося в натянутом состоянии вдоль местной вертикали благодаря градиенту гравитационного поля Земли. Далее будем называть этот режим движения троса номинальным. В номинальном режиме движения ось z, направленная вдоль натянутого троса, коллинеарна оси Cζ (Фиг. 1), направленной вдоль радиуса-вектора R=O_EC=Rζ₀ центра масс троса относительно центра Земли О_E.

Орбита точки С предполагается круговой и экваториальной. Оси Cξ и Сη, направленные соответственно по касательной к орбите в сторону движения точки С и по нормали к плоскости орбиты, образуют вместе с осью Сζ орбитальную систему координат Сξηζ. В инерциальном пространстве орбитальная система координат поворачивается с угловой скоростью ω₀=ω₀ η₀.

Тела, присоединенные к концам троса, считаются точечными, а их вращательным движением можно пренебречь ввиду малости отношения характерного размера тела к длине троса. Упругие деформации троса также не рассматриваются. Трос считается натянутым, а его либрационное движение относительно центра масс не влияет на его орбитальное движение.

Таким образом, будем моделировать ЭДТС тонким стержнем с массой m₀ и с точечными массами m₁ и m₂ на концах и для краткости называть ее связкой. Координаты масс m_k обозначим z_k (k=1,2). Координаты центров зарядов q_k также будем считать совпадающими с z_k.

В системе главных центральных осей инерции Cxyz (орты i, j, k) тензор инерции связки имеет вид J=diag (А, А, 0), где .

Взаимную ориентацию осей систем координат Сξηζ и Cxyz зададим с помощью матрицы направляющих косинусов

так, что

, , .

Кинематическими характеристиками вращательного движения связки являются: абсолютная угловая скорость ω и угловая скорость связки относительно орбитальной системы координат ω'=pi+qj+rk. Эти величины связаны соотношением ω=ω'+ω₀, которое в проекциях на оси Cxyz имеет вид

Рассмотрим моменты сил, действующих на связку. В центральном ньютоновском гравитационном поле на связку действует гравитационный момент М_G [19]. В рассматриваемой задаче, с учетом принятых обозначений, проекции гравитационного момента на оси Cxyz имеют вид:

При вычислении главного момента сил Лоренца, действующих на заряды q₁ и q₂, воспользуемся простейшей аппроксимацией этого момента [20], учитывающей точечный характер зарядов:

Здесь , , ω_Е - угловая скорость суточного вращения Земли. В условиях моделирования МПЗ прямым магнитным диполем , где - гауссов коэффициент, R_E - средний радиус Земли. В проекциях на оси Cxyz получаем:

Главный момент сил Ампера вычислим по формуле [1]

где ρ - радиус-вектор, проведенный из точки С в точку троса с текущей координатой z, I - величина силы тока в проводнике. Принимая I=const, в результате интегрирования (6) получаем

В качестве дифференциальных уравнений вращательного движения связки относительно центра масс будем использовать динамические уравнения Эйлера

и кинематические уравнения Пуассона

Для отыскания равновесных положений связки в орбитальной системе координат будем рассматривать направляющие косинусы как неизвестные постоянные величины, а проекции относительной угловой скорости p, q, r будем полагать равными нулю в уравнениях (2), (8), (9). Динамические уравнения примут вид

Из уравнений (9), (10) следует, что номинальный режим движения связки, соответствующий значению γ₃=1, имеет место при z₁=z₂.

Для решения вопроса о существовании других возможных положений равновесия связки в орбитальной системе координат перейдем в уравнениях (10) от направляющих косинусов к углам Эйлера ϕ (угол собственного вращения вокруг оси z), ϑ (угол нутации - угол между осями Cz и Cζ), ψ (угол прецессии - вращения вокруг оси Cζ) по формулам

β₁=sinψ cosϕ+sinϕ cosψ cosϑ, β₂=-sinψ sinϕ+cosϕ cosψ cosϑ,

β₃=-cosψ sinϑ, γ₁=sinϕ sinϑ, γ₂=cosϕ sinϑ, γ₃=cosϑ.

Затем осуществим линейное неособенное преобразование получаемых уравнений. Первое уравнение умножим на -sinϕ, второе уравнение умножим на cosϕ и сложим оба уравнения. После этого первое уравнение умножим на cosϕ, второе уравнение умножим на sinϕ и сложим оба уравнения. Получим систему

Из системы (11) следует, что интересующий нас номинальный режим движения ϑ=0 существует лишь при условии

В дальнейшем будем считать это условие выполненным. Ввиду однородности троса условие (12) выполняется при z₁=-z₂, m₁=m₂. В этом случае .

Из системы (11) следует также, что кроме номинального режима движения ϑ=0 теоретически возможны также и другие («косые») положения равновесия связки в орбитальной системе координат, определяемые из условий:

где . С учетом соотношения z₁=-z₂ получаем:

,

Заметим, что cosϑ₁<cosϑ₂. Следовательно, если параметры связки удовлетворяют неравенству

то «косые» положения равновесия не реализуются и единственным возможным положением равновесия связки в орбитальной системе координат остается номинальный режим ϑ=0. Неравенство (15) было исследовано численно. На Фиг. 3 приведен пример расчетов, выполненных для следующих значений параметров:

R=7⋅10⁶ м, q₁=-5⋅10^-2 Кл, q₂=5⋅10^-2 Кл.

На Фиг. 3 представлена граница области существования «косых» положений равновесия

По горизонтальной оси отложены значения m₀/6+m₂, по вертикальной - значения z₂. Если длины и массы таковы, что изображающая точка лежит ниже кривой на графике, то неравенство (15) выполняется. Например, пусть z₂=100 м, z₁=-100 м, погонная масса троса γ=2⋅10^-3 кг/м, m₁=m₂=16 кг. Тогда неравенство (15) выполнено.

Рассмотрим вопрос об устойчивости номинального режима движения связки. Для этого обратимся к исходным уравнениям Эйлера (8) и, вводя обозначение

, перепишем первые два из них в виде

Несложно проверить, что имеет место равенство

,

где производная в левой части равенства вычисляется в силу системы (16). Переходя от абсолютных угловых скоростей ω_x, ω_y к относительным угловым скоростям p, q, перепишем это равенство в виде

.

Затем, вводя новую переменную Δ=1-γ₃, представляющую собой меру отклонения связки от номинального режима движения γ₃=1, перепишем последнее соотношение в виде

.

Отсюда следует, что если учесть условие (13), то а=0 и получаем первый интеграл

Поскольку выбором q₁z₁+q₂z₂>0 всегда можно обеспечить выполнение неравенства L>0, то, функция V(α₃, β₃, Δ, p, q) является положительно определенной. Принимая ее в качестве функции Ляпунова, приходим к выводу об устойчивости номинального режима движения связки по отклонениям α₃, β₃, Δ и угловым скоростям p, q на основании теоремы Ляпунова об устойчивости.

Замечание 1. Увеличение параметра L>0, обусловленного наличием лоренцева момента, расширяет область устойчивости номинального режима движения связки. Тем самым подтверждается стабилизирующий эффект лоренцева момента, возбуждаемого за счет зарядов на концах троса, что служит обоснованием применения заявляемого способа построения ЭДТС.

Замечание 2. Наличие диссипации в ЭДТС способно превратить устойчивое положение равновесия троса в асимптотически устойчивое положение равновесия. Поэтому целесообразен учет нагрева троса за счет омического сопротивления и последующего рассеяния энергии ЭДТС в окружающее пространство в виде тепла [6]. Перспективно также применение различных известных демпфирующих устройств [1], создающих момент, пропорциональный относительной угловой скорости.

Замечание 3. Из невыполнения неравенства (15) не следует невозможность стабилизации ЭДТС вдоль местной вертикали. Выполнение условия (15) гарантирует лишь отсутствие других положений равновесия троса в силу выбранной математической модели.

Все сформулированные выше выводы подтверждаются серией численных экспериментов, моделирующих процесс стабилизации ЭДТС в режиме вертикального расположения троса. Для иллюстрации численного моделирования процесса стабилизации выбран пример конструкции ЭДТС, содержащей трос длиной 200 м, обладающий погонной массой γ=2⋅10^-3 кг/м и проводящий ток I=2А. Масса на нижнем конце троса m₁=55 кг, масса на верхнем конце троса m₂=50 кг. Центр заряда коллектора на нижнем конце троса имеет координату z₁=-95 м, центр заряда коллектора на верхнем конце троса имеет координату z₂=105 м. Центр масс ЭДТС движется по круговой экваториальной орбите радиуса R=7⋅10⁶ м. Модельный диссипативный момент пропорционален относительной угловой скорости ЭДТС M_D=-hJω₀ω' и содержит множителем малый параметр, выбранный равным h=0.001.

Фиг. 4-6 иллюстрируют движение ЭДТС с нулевыми зарядами на коллекторах. В начальный момент времени трос был отклонен от местной вертикали на угол 1 рад в плоскости (η, ζ) и отпущен без начальной угловой скорости относительно орбитальной системы координат. Вертикальное положение троса оказывается неустойчивым, что наглядно демонстрируется поведением направляющего косинуса γ₃ (Фиг. 4), все сильнее отклоняющегося от целевого значения γ₃=1 под действием Амперова момента, а также поведением компонент относительной угловой скорости, отнесенной к орбитальной угловой скорости (Фиг. 5). Заметим, что при этом во все время движения величина возмущающего Амперова момента остается малой (Фиг. 6) - на 2 порядка меньше величины гравитационного момента (Фиг. 7), стремящегося стабилизировать ЭДТС вдоль местной вертикали.

Фиг. 8-11 иллюстрируют движение ЭДТС с ненулевыми зарядами на коллекторах: q1=-0.05 Кл, q2=0.05 Кл. Все остальные параметры ЭДТС и начальные условия ее движения сохранены без изменений, как в случае Фиг. 4-7. Результаты численного интегрирования показывают, что направляющий косинус γ₃ стремится к целевому значению γ₃=1 (Фиг. 8), а компоненты относительной угловой скорости, отнесенной к орбитальной угловой скорости, стремятся к нулю (Фиг. 9). При этом диссипативный момент остается весьма малым по величине (на порядок меньше возмущающего - Амперова момента и на 3 порядка меньше гравитационного момента) во все время движения (Фиг. 10) и по этой причине соответствующая ему кривая сливается с горизонтальной осью на Фиг. 11, где приведены модули всех действующих на ЭДТС моментов.

На всех Фиг. 4-11 по горизонтальной оси откладывается безразмерный угол - аргумент широты u=ω₀ t. Заметим, что для иллюстрации численного моделирования выбраны «худшие» значения параметров ЭДТС, для которых условие (15) не выполняется. Более того, не выполняется даже соотношение z₁=-z₂, что позволяет рассматривать Амперов момент как постоянно действующее возмущение, естественным образом возникающее в данной задаче.

Полученные результаты свидетельствуют о том, что предложенный способ может быть осуществлен с помощью известных технических средств, позволяющих поддерживать электростатические заряды на концевых коллекторах ЭДТС.

Устройство стабилизации электродинамической тросовой системы для удаления космического мусора, содержащее проводящий электроизолированный трос, отличающееся тем, что один конец троса снабжен коллектором положительно заряженных частиц, соединенным с концевым телом троса через электроизолятор, внутри которого расположен не менее чем один электронный эмиттер, генерирующий электронный пучок с коллектора положительно заряженных частиц, второй конец изолированного троса снабжен коллектором отрицательно заряженных частиц, соединенным с концевым телом троса через электроизолятор, внутри которого расположен не менее чем один электронный эмиттер, генерирующий электронный пучок с концевого тела троса, а существование, единственность и устойчивость положения равновесия троса в натянутом состоянии вдоль местной вертикали обеспечивается выбором таких параметров троса и присоединенных к нему вышеописанных устройств, для которых расстояния от центра масс системы до центров заряженных коллекторов одинаковы и выполняется неравенство

где R_E - средний радиус Земли, - гауссов коэффициент, ω₀ - орбитальная угловая скорость центра масс, ω_E - угловая скорость суточного вращения Земли, q₁ - отрицательный заряд, накопленный коллектором на нижнем конце, q₂ - положительный заряд, накопленный коллектором на верхнем конце, R - радиус орбиты центра масс, m₀ - масса троса, m₂ - масса устройств, присоединенных к тросу на верхнем конце, z₂ - расстояние от центра масс системы до центра масс устройств, присоединенных к тросу на верхнем конце.