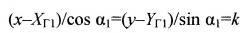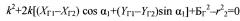Способ позиционирования объекта засечкой азимута с первого измерительного пункта и угла места с дальностью - со второго

Способ позиционирования объекта засечкой азимута с первого измерительного пункта и угла места с дальностью - со второго

Иллюстрации

Показать все

Реферат

Изобретение относится к области обнаружения и определения координат различных объектов (летательных аппаратов различного назначения, снарядов, ракет) и может быть использовано в военной технике.

В настоящее время известны различные способы определения координат объектов с использованием способов передачи и приема радиосигналов наземных радиомаяков (патент Российской Федерации №2436232) [1], способ триангуляции целей (патент Российской Федерации №2423720) [2]. Недостатками данных способов являются сложность обработки информации от пунктов обнаружения объектов, использование только активного радиолокационного диапазона электромагнитных волн, большое число измеряемых параметров.

Способ автоматизированного определения координат беспилотных летательных аппаратов (патент Российской Федерации №2523446) [3] заключается в применении камер кругового обзора, видеомонитора, ЭВМ и лазерного дальномера для подсветки летательного аппарата. Камеры кругового обзора размещают симметрично и направляют в разные стороны, так чтобы вести наблюдение на 360° по горизонту в оптическом диапазоне электромагнитных волн. Появление летательного аппарата фиксируется автоматически как помеха, возникающая на кадре видеопоследовательности относительно предыдущего, а полученные данные обрабатываются на ЭВМ, где рассчитываются угловые координаты летательного аппарата относительно центра углоизмерительного устройства, которое с помощью поворотных механизмов направляет лазерный дальномер на летательный аппарат для измерения дальности до него. Измеренная дальность поступает на устройство обработки и отображения информации, где происходит определение прямоугольных координат объекта (X_ГО; h_ГО; Y_ГО).

Способ определения координат летательных аппаратов на основе использования двух дирекционных углов и одного угла места (патент Российской Федерации №260149) [4] заключается в измерении указанных параметров с двух пунктов сопряженного наблюдения, с последующим пересчетом величин (α₁, α₂, ε₂)в координаты объекта.

Общим недостатком данных способов определения координат летательных аппаратов является избыточность информации о положении объекта, неполное использование данных измерений и, как следствие, немаксимальная точность, а также отсутствие способов оценки точности координат.

Задачей, стоящей перед настоящим изобретением, является разработка способа получения координат измеряемого объекта при минимально необходимой для получения результата информации и оценка точности позиционирования объекта.

Поставленная задача решается следующим образом.

В настоящее время дальномерно-пеленгационный метод определения координат объектов широко распространен в практике оптических и радиолокационных внешнетраекторных измерений (рис. 1). Он основан на измерении угловых координат объекта в горизонтальной (азимут А или дирекционный угол α) и вертикальной плоскостях (угол места ε), а также дальности до него R (рис. 1). В простейшем случае организации таких измерений достаточно одного измерительного пункта с известными координатами (X_Г; h_Г; Y_Г), чтобы однозначно определить пространственные координаты летательного аппарата по зависимостям

С целью повышения надежности получения траекторией информации количество измерительных пунктов увеличивают до двух-трех. При этом на каждом из них проводятся аналогичные измерения трех сферических координат объекта (α_i, ε_i, R_i). В этом случае возникает некоторая избыточность информации, определяемая разностью между числом регистрируемых параметров и числом степеней свободы объекта равном трем. В случае двух измерительных пунктов синхронно регистрируется шесть параметров (α₁, ε₁, R₁) (α₂, ε₂, R₂), где индекс показывает номер измерительного пункта. Чаще всего вторая тройка чисел используется по аналогии с первой для вычисления координат объекта по зависимостям (1) и служит только для контроля вычислений. В тоже время любая тройка чисел из шести измеренных параметров (α₁, ε₁, R₁, α₂, ε₂, R₂), позволяет определить координаты объекта. При таком способе обработки большая часть полученной траекторной информации теряется, а возможности измерительной техники используются не в полной мере. В случае получения неполной информации с измерительных средств использовать канонические зависимости дальномерно-пеленгационного способа (1) не представляется возможным. Поэтому возникает необходимость разработки способа определения положения объекта при неполных измерениях, одним из которых является случай регистрации трех величин - α₁, ε₂, R₂ или α₂, ε₁, R₁. Все дальнейшие выкладки для определенности выполнены для первого случая, а второй вариант можно получить из первого путем замены индексов «1» на «2» и «2» на «1».

Необходимо отметить, что при использовании тройки чисел α₁, ε₁, R₂ имеет место совершенно иная геометрическая картина измерений. Здесь в отличие от рассматриваемого случая на первом измерительном пункте должны быть определены две величины (α₁; ε₁), а дальность до объекта измерения R₂ определяется со второго измерительного пункта. В исследуемом варианте производства внешнетраекторных измерений на первом измерительном пункте регистрируются направление на исследуемый объект α₁, а на втором - угол места ε₂ и дальность до него R₂. Данное обстоятельство требует решения принципиально иной геометрической задачи.

Математически задача формулируется так: пусть известны географические координаты первого измерительного пункта ИП-1 (X_Г1; h_Г1; Y_Г1), с которого измерен дирекционный угол на объект α₁, а также географические координаты второго измерительного пункта ИП-2 (X_Г2; h_Г2; Y_Г2), на котором измерена дальность до объекта R₂ и его угол места ε₂. Необходимо найти координаты объекта (X_ГО; h_ГО; Y_ГО).

Геометрическим местом точек, для которых α₁=const, является вертикальная полуплоскость, проходящая через измерительный пункт ИП-1. Геометрическим местом точек пересечения сферы и прямого вертикального круглого конуса с единым центром является окружность радиуса r₂, лежащая в горизонтальной плоскости, на высоте от ИП-2 (рис. 2). Аппликата точки пересечения может быть найдена по зависимости

.

Радиус окружности, получаемой в сечении горизонтальной плоскости на высоте h_ГО и конуса, можно найти по зависимости, очевидной из построения

.

Таким образом, уравнение горизонтальной окружности, полученной пересечением сферы и конуса, имеет вид

Уравнение прямой, принадлежащей вертикальной полуплоскости и горизонтальной плоскости, содержащей окружность сечения, определяется выражением

где k - параметр.

Выражая из последней зависимости величины x и y и подставляя их в уравнение окружности (2), получим

5

или

.

Обозначая через Б_Г расстояние между измерительными пунктами в горизонтальной плоскости или горизонтальную базу

и упрощая полученное выражение, будем иметь

Это квадратное уравнение относительно параметра k. Найдем его корни

.

Если , то полуплоскость пересекает окружность в двух точках, если , то полуплоскость не пересекает окружность, если , то полуплоскость касается окружности в одной точке. При двух общих точках выбор нужного решения можно производить по степени близости (удалению) расчетного положения объекта до приближенного положения или положения, полученного другим способом.

Решение квадратного уравнения имеет вид

.

Таким образом, окончательно координаты объекта можно найти по зависимостям

Так как итоговая зависимость результатов расчетов от аргументов достаточно сложная, то для оценки точности координат целесообразно использовать метод линеаризации. В условиях рассматриваемого способа срединную ошибку координаты X_Г можно найти по следующей зависимости:

где Е[X_Г] - срединная ошибка определения координаты X_г объекта;

- частная производная координаты X_г по дирекционному углу. Она показывает, насколько изменится расчетное значение X_г при изменении α₁ на единицу;

E[α₁], Е[ε₂], E[R₂] - срединные ошибки измерений дирекционного угла, угла места и дальности соответственно. Аналитические зависимости для расчета срединных ошибок координат h_г и Y_г имеют аналогичный вид

По этой же причине частные производные, входящие в выражения (4)-(5) целесообразно определять по формулам численного дифференцирования по трем точкам

или по двум точкам

Другие частные производные , …, целесообразно определять по зависимостям аналогичным (6), (7).

Таким образом, предлагаемый способ определения положения объекта засечкой с двух измерительных пунктов по азимуту, углу места и дальности, позволяет определять положение летательного аппарата при дальномерно-пеленгационном способе организации внешнетраекторных измерений с двух измерительных пунктов в оптическом и радиолокационном диапазонах электромагнитных волн при минимально необходимой информации и оценивать его точность.

Источники информации

1. Панов В.П., Приходько В.В. Способ передачи и приема радиосигналов наземных радиомаяков. - М.: ФИПС. Патент на изобретение №2436232, 10.12.2011 г.

2. Безяев B.C. Способ триангуляции целей. - М.: ФИПС. Патент на изобретение №2423720, 10.07.2011 г.

3. Шишков С.В. Способ автоматизированного определения координат беспилотных летательных аппаратов. - М.: ФИПС. Патент на изобретение №2523446, 26.05.2014 г.

4. Шишков С.В. Способ определения координат летательных аппаратов на основе использования двух дирекционных углов и одного угла места. - М.: ФИПС. Патент на изобретение №2601494, 20.04.2015 г.

Способ определения положения летательного аппарата в декартовой системе координат на основе засечки дирекционного угла α₁ с первого измерительного пункта с координатами (Х_Г1; h_Г1, Y_Г1) и угла места ε₂ с дальностью R₂ - со второго измерительного пункта с координатами (Х_Г2; h_Г2, Y_Г2) с последующей обработкой внешнетраекторной информации путем решения геометрической задачи пересечения вертикальной полуплоскости, проходящей через первый измерительный пункт, прямого, круглого конуса и сферы с центрами во втором измерительном пункте, алгебраически сводящейся к поиску корней квадратного уравнения относительно параметра k вида

k²+2k[(X_Г1-Х_Г2)cosα₁+(Y_Г1-Y_Г2)sinα₁]+Б_Г²-r²₂=0,

и последующим определением искомых координат летательного аппарата по аналитическим зависимостям: Х_ГО=ƒ_X=X_Г1+k_1,2cosα₁; h_ГО=ƒ_h=h_Г2+R₂sinε₂; Y_ГО=ƒ_Y=Y_Г1+k_1,2sinα₁.