Система релятивистской квантовой криптографии

Система релятивистской квантовой криптографии

Иллюстрации

Показать все

Реферат

Изобретение относится к области квантовой криптографии, а именно квантового распределения ключей - QKD (см., например, V. Scarani, H. Bechmann-Pasquinucci, N.J. Cerf, М. Dusek, N. Lutkenhaus, and M. Peev, "The security of practical quantum key distribution," Rev. Mod. Phys., vol. 81, no. 3, pp. 1301-1350, 2009). Благодаря использованию фундаментальных принципов квантовой физики, становится возможным обмен секретными ключами по открытому квантовому каналу связи, при этом гарантируя секретность получаемых ключей. Любые попытки подслушивания учитываются в протоколе такого распределения ключей и становятся известными абонентам - участникам протокола. Среди множества известных протоколов квантового распределения ключей, настоящее изобретение относится к так называемому релятивистскому протоколу квантового распределения ключей, использующему квантовый канал связи по открытому пространству.

Особенность релятивистского протокола заключается в необходимости реализации интерферометра с большой (порядка 10 нс) временной задержкой. Такие интерферометры недостаточно стабильны из-за большой разности длин оптических путей и, в общем случае, требуют активной подстройки. Известно решение данной проблемы с использованием двухпроходной схемы (I.V. Radchenko, K.S. Kravtsov, S.P. Kulik, and S.N. Molotkov, "Relativistic quantum cryptography," Laser Phys. Lett., vol. 11, no. 6, p. 065203, 2014), в которой один и тот же интерферометр используется и для кодирования и для декодирования квантовых посылок, ввиду чего он оказывается автоматически согласованным. Однако, указанная двухпроходная конфигурация существенно ограничивает допустимую частоту передачи квантовых посылок и приводит к снижению эффективности всей системы в целом.

Предлагаемая схема использует однопроходную конфигурацию, в которой приемный интерферометр непрерывно подстраивается, обеспечивая требуемый фазовый сдвиг между двумя плечами интерферометра. Подстройка интерферометра осуществляется с использованием Байесовского метода реконструкции разности фаз по отсчетам однофотонного детектора на выходе интерферометра. В отличие от других способов подстройки интерферометра, предлагаемая схема практически не снижает эффективность работы всей системы, не требует каких-либо еще источников излучения, кроме источника света в квантовом канале, а также не нуждается в дополнительных детекторах. Кроме того, используемый однопроходный режим работы всей системы квантовой криптографии потенциально более стоек к активным атакам на оборудование системы квантового распределения ключей.

Технической задачей, решаемой настоящим изобретением, является организация подстройки приемного интерферометра в однопроходной схеме релятивистского квантового распределения ключей с использованием уже имеющихся в системе ресурсов, а именно, однофотонного детектора и фазового модулятора.

Поставленная задача решается путем использования временных окон между квантовыми посылками данных для реконструкции разности фаз с помощью Байесовского статистического метода. При этом используется тот же источник сигнала и однофотонный детектор, что и для данных. Управление интерферометром осуществляется фазовым модулятором, который также выполняет двойную роль: обеспечивает демодуляцию данных и поддерживает требуемую разность фаз между плечами интерферометра.

Предлагаемый Байесовский алгоритм осуществляет статистическую связь между состоянием фазового модулятора и частотой отсчетов однофотонного детектора, и на основе анализа статистических данных оптимальным образом выбирает фазовый сдвиг, обычно соответствующий полностью деструктивной интерференции, для корректного декодирования передаваемых данных. Этапы подстройки интерферометра и передачи данных сменяют друг друга, обеспечивая глобальную непрерывность поддержания системы в работоспособном состоянии.

Краткое описание чертежей.

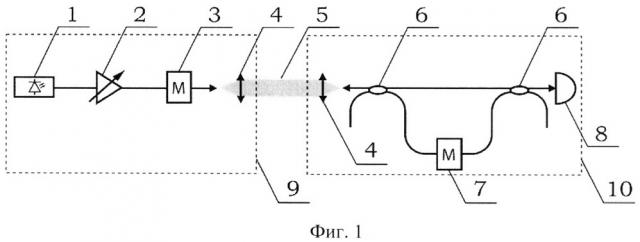
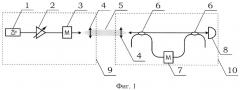
На фиг. 1 представлена для примера схема реализации системы релятивистского квантового распределения ключей, работающей по атмосферному каналу связи. Данная схема представляет одну из возможных реализаций системы релятивистской квантовой криптографии, и никоим образом не ограничивает применимость настоящего изобретения. Система естественным образом разделяется на две части: передающую 9 и приемную 10, соединенные квантовым каналом связи по открытому пространству 5.

Передающая часть 9 состоит из передающего лазера 1, переменного аттенюатора 2, фазового модулятора 3 и телескопа 4, выполняющего роль передающего телескопа. В данной конфигурации передающий лазер 1 должен быть достаточно узкополосным и обеспечивать длину когерентности излучения много большую, чем разность оптических длин в интерферометре задержки на приемной стороне. Аттенюатор 2 используется для ослабления сигнала до уровня отдельных фотонов, определяемого используемым протоколом релятивистского квантового распределения ключей. Фазовый модулятор 3 служит для формирования посылок согласно протоколу релятивистского квантового распределения ключей. Передающий телескоп должен с незначительными оптическими потерями сформировать выходной пучок передающей системы, который, распространяясь в открытом пространстве (атмосфере), соединяет передающую и приемную станции.

Приемная часть 10 включает телескоп 4, выполняющий роль приемного телескопа, интерферометр задержки, состоящий из симметричных волоконных светоделителей (каплеров) 6 и фазового модулятора 7, а также однофотонный детектор 8. Настоящее изобретение непосредственно относится к непрерывной подстройке интерферометра задержки, а именно предлагает определенный алгоритм совместной работы фазового модулятора 7 и однофотонного детектора 8 во временных окнах между посылками данных согласно протоколу релятивистского квантового распределения ключей.

На фиг. 2 представлена возможная схема реализации Байесовского алгоритма непрерывной подстройки фазы интерферометра задержки в системе релятивистской квантовой криптографии. Текущее значение распределения вероятностей для актуальной расстройки фазы подается на вход (изначально, вместо него берется априорное распределение вероятностей) блока 1. Выбирается произвольное значение фазы ϕ и устанавливается на фазовом модуляторе. Затем в течение времени ΔТ проводится регистрация сигнала однофотонным детектором. Результат операции (бинарный: отсчет был или его не было) используется в блоке 2, в котором производится умножение текущего распределения вероятностей на соответствующий Байесовский множитель. В блоке 3 вычисляется наиболее вероятное значение по распределению для фазовой расстройки интерферометра и устанавливается на фазовом модуляторе. После этого в блоке 4 проводится квантовое распределение ключей. Длительность данного блока определяется, в первую очередь, скоростью случайной расстройки фазы из-за ее медленных флуктуаций. В блоке 5 эта дополнительная расстройка учитывается в виде диффузии фазы, пропорциональной времени, затраченному на все предыдущие шаги. Таким образом модифицированное распределение вероятностей снова подается на вход системы и процесс повторяется.

Осуществление изобретения.

Квантовая механика открывает возможность распределения секретных ключей, гарантируя отсутствие подслушивания или утечки информации третьим лицам. Данное направление традиционно называется квантовая криптография или квантовое распределение ключей (QKD). Относительно недавно было показано, что использование вдобавок к квантовой механике принципа относительности позволяет существенно расширить область параметров (в первую очередь, потери в канале связи и требования к квантовому источнику), в которой может гарантироваться безусловная секретность переданных ключей (S.N. Molotkov and S.S. Nazin, "The role of causality inensuring the ultimate security of relativistic quantum cryptography," JETP Lett., vol. 73, no. 12, pp. 682-687, 2001). Соответствующие способы распределения секретных ключей получили название релятивистского квантового распределения ключей. Настоящее изобретение мотивировано экспериментальными исследованиями по данной тематике.

Для конкретики, рассмотрим простейшую систему релятивистской квантовой криптографии, показанную на фиг. 1. Передающая часть содержит узкополосный лазерный источник 1. Для простоты будем считать его монохроматическим. Излучение лазера ослабляется аттенюатором 2 до уровня мощности I₀, проходит через фазовый модулятор 3 и передается на принимающую станцию 10 по каналу связи в открытом пространстве.

Основой принимающей станции является интерферометр задержки, образованный симметричными светоделителями 6 и фазовым модулятором 7. Интерферометр задержки может быть выполнен, например, в виде оптоволоконной структуры с использованием сварных оптоволоконных светоделителей (каплеров). Фазовый модулятор может быть, например, электро-оптическим фазовым модулятором на основе ниобата лития, или любым другим подходящим по параметрам. Относительная фаза между плечами интерферометра настраивается так, чтобы при отсутствии сигналов на фазовых модуляторах на выходе к однофотонному детектору была полностью деструктивная интерференция. Обозначим относительную задержку между плечами интерферометра как Т. Для работоспособности протокола релятивистской квантовой криптографии данная величина должна быть порядка 10 нс или больше, что связано с более медленным распространением света в условиях земной атмосферы по сравнению со скоростью света в вакууме.

Для генерации сырого ключа используется следующий протокол: передающая станция в заранее оговоренные моменты времени t_n случайно и с равной вероятностью выбирает один из двух вариантов работы фазового модулятора 3. Либо на время τ<Т фаза оптического сигнала изменяется на π, либо фаза остается неизменной. На приемной стороне выполняется та же самая процедура с фазовым модулятором 7, но в моменты времени t_n+Δt, где Δt - время распространения сигнала от фазового модулятора 3 до фазового модулятора 7. Таким образом, временные окна, в которых производится фазовая модуляция сигнала полностью перекрываются. В результате действия такого протокола появление фотона в однофотонном детекторе 8 возможно только в случае, когда передающая и приемная стороны выбрали противоположные варианты работы фазовых модуляторов. Следовательно, при появлении отсчета в детекторе 8 принимающая сторона, зная свой вариант работы фазового модулятора, может сделать вывод относительно работы модулятора передающей стороны.

Обозначив наличие и отсутствие фазовой модуляции сигнала за 0 и 1 соответственно, приемная сторона, получив отсчет в детекторе 8, узнает значение соответствующего бита информации на передающей стороне. Серия таких посылок приводит к появлению у абонентов сырого ключа, который затем может быть очищен от возможных ошибок и информации, которая могла стать доступна третьим лицам.

Принципы, приводящие к секретности распределенного таким образом ключа, опираются на два фундаментальных требования. Во-первых, интенсивность излучения I₀ должна быть такой, чтобы ожидаемое число фотонов за время τ было существенно меньше единицы: τI₀/hν<<1. Таким образом, доступная классическая информация, согласно теореме Холево, в каждой посылке существенно меньше 1 бита, а значит подслушиватель, в принципе, не может получить доступ ко всему переданному сырому ключу, при условии, что он не мог сделать предварительной селекции того, что пропускать через канал, а что заблокировать. Во-вторых, приемная сторона производит регистрацию фотонов в точно определенные моменты времени, соответствующие пролету через канал со скоростью света и в первом из двух возможных временных окон. Все отстающие посылки игнорируются. Таким образом, осуществляется запрет на селекцию состояний в канале со стороны третьих лиц. Более фундаментальное описание с доказательствами приведенных рассуждений можно найти в следующих работах: S.N. Molotkov, "Relativistic quantum cryptography," JETP, vol. 112, no. 3, pp. 370-379, 2011; S.N. Molotkov, "Relativistic quantum cryptography for open space without clock synchronization on the receiver and transmitter sides," JETP Lett., vol. 94, no. 6, pp. 469-476, 2011; S.N. Molotkov, "On the resistance of relativistic quantum cryptography in open space at finite resources," JETP Lett., vol. 96, no. 5, pp. 342-348, 2012.

Остановимся более подробно на вопросе настройки интерферометра, являющимся ключевым в данном изобретении. Относительную фазу интерферометра можно изменять любым видом контроля фазы в одном или двух плечах интерферометра. Для простоты, но без ограничения общности высказываемых здесь принципов изобретения, будем считать, что настройка интерферометра производится тем же фазовым модулятором 7, который участвует в протоколе распределения ключей. Для этого, на нем устанавливается постоянный сдвиг фазы ϕ₀, который обеспечивает деструктивную интерференцию на выходе однофотонного детектора. При этом, для дополнительной фазовой модуляции согласно протоколу распределения ключей сдвиг фазы на π осуществляется относительно данного значения ϕ₀.

Ввиду особенностей распространения оптических сигналов, практически при любом устройстве интерферометра задержки, желаемая фаза ϕ₀ флуктуирует от времени, что существенно усложняет реализацию приведенного протокола. Это связано с такими процессами как механическая вибрация, звуковые колебания, изменение температуры или напряжения в материалах, и др. Обычно достаточно просто устранить высокочастотные колебания фазы, обеспечив адекватную звуко- и термоизоляцию интерферометра задержки. Однако, медленные (с характерными временами порядка минуты) флуктуации фазы требуют активной подстройки интерферометра, которая может быть осуществлена согласно настоящему изобретению.

Для реализации отслеживания требуемой фазы ϕ₀ предлагается использовать следующие соображения. Поскольку при выставлении фазы ϕ₀ на фазовом модуляторе интерферометр настроен так, что интенсивность сигнала, попадающего на однофотонный детектор равна нулю, зависимость этой интенсивности от произвольно выставленной фазы ϕ на фазовом модуляторе описывается соотношением:

1(ϕ)=αI₀[1-cos(ϕ-ϕ0)]/2,

где α - обозначает потери сигнала во всем оптическом тракте от аттенюатора 2. Например, при ϕ=ϕ₀+π получаем полностью конструктивную интерференцию на выходе к детектору, следовательно, вся доступная интенсивность αI₀ попадает в детектор. Измеряя интенсивность на детекторе при различных значениях ϕ, относительно несложно найти искомое значение ϕ₀.

Основная сложность состоит в том, что уровень сигнала αI₀ является настолько слабым, что он детектируется как отдельные фотоны, т.е. дискретные события, происходящие случайно и следующие модели Пуассоновского процесса.

Подходящим инструментом для нахождения фазы ϕ₀ является Байесовская статистическая модель. Для простоты рассмотрим сначала стационарный случай, в котором будем считать ϕ₀ постоянным на протяжении всего измерения. В начальный момент, предполагается, что фаза ϕ₀ может быть любой допустимой с одинаковой вероятностью, следовательно, можно определить априорную вероятность как ρ₀(ϕ₀)=(2π)^-1 где ϕ₀ принимает любые возможные значения от 0 до 2π. Далее, измерение числа фотоотсчетов в однофотонном детекторе производится в течение одинаковых промежутков времени ΔТ. Вероятность получения отсчета равняется р₁(ϕ₀)=1-ехр[-I_ϕ0(ϕ)ΔT/hυ], а вероятность отсутствия отсчетов за этот же интервал времени равна р₀(ϕ₀)=ехр[-I_ϕ0(ϕ)ΔT/hυ], где ϕ - установленный фазовый сдвиг на фазовом модуляторе, а I_ϕ0(ϕ) - ожидаемая интенсивность сигнала при конкретном значении ϕ₀. Согласно используемому Байесовскому подходу после каждого проведенного измерения в зависимости от его исхода i={0,1} текущее распределение вероятности ρ(ϕ₀) обновляется согласно следующему соотношению:

ρ(ϕ₀)→ρ(ϕ₀)p_i(ϕ₀).

В результате, плоское априорное распределение вероятности постепенно сужается вокруг истинного значения ϕ₀. Для достижения быстрой сходимости требуется выбирать различные значения текущего сдвига фаз в фазовом модуляторе ϕ. Оптимальная неадаптивная модель подразумевает выбор случайного значения ϕ для каждого следующего измерения. Возможен также адаптивный вариант выбора значения ϕ, когда его выбор зависит от текущего распределения вероятности ρ(ϕ₀).

Процесс измерения продолжается требуемое число шагов для получения значения ϕ₀ с требуемой точностью (распределение вероятности становится настолько узким, что вероятность отличия ϕ₀ от среднего значения больше заданной фазовой ошибки становится меньше заданного порога, например, 10^-5). После того как величина ϕ₀ определена, система может переключаться в режим квантового распределения ключей, так как знание величины ϕ₀ позволяет обеспечить требуемую разность фаз в плечах интерферометра с помощью фазового модулятора.

Случай медленно изменяющейся величины ϕ₀ может быть реализован различными способами, например, но не ограничиваясь следующими тремя:

1. Фаза периодически подстраивается как и для случая неизменного фазового сдвига. Дальнейший процесс квантового распределения ключей продолжается столько времени, сколько ожидается до существенного изменения величины ϕ₀. После этого процедура определения фазы повторяется вновь. Такой способ отличается простотой реализации, однако не максимально эффективно использует полученную информацию: на каждом шагу вся известная информация отбрасывается и заменяется плоским априорным распределением.

2. Фаза находится по результату лишь последних N измерений, т.е. на каждом шаге распределение вероятности вычисляется по следующей формуле , где исходы измерения k шагов назад обозначены как i_-k. В этом случае сохраняется непрерывность процесса и он может более просто перемежаться с передачей данных: после каждого измерения может следовать определенное число квантовых посылок для квантового распределения ключей. Негативным эффектом данного метода является избыточность вычислительных операций и используемой памяти, особенно при большом N.

3. Для устранения недостатков предыдущего варианта может использоваться модель фазовой диффузии, когда на каждом шаге распределение вероятности вдобавок к Байесовскому множителю претерпевает фазовую диффузию, что снижает наше знание величины ϕ₀ и соответствует медленным случайным флуктуациям фазы. Таким образом, через большое время постепенно установится равновесие между информацией, получаемой после каждого измерения, и потерей информации ввиду диффузии фазы из-за ее медленных флуктуаций. Такой метод не требует больших вычислительных ресурсов и при этом остается квазинепрерывным по времени. Он, по-видимому, позволяет получить одну из лучших возможных оценок значения ϕ₀ после каждого измерения. Последний вариант оценки фазы интерферометра в одном из возможных вариантов реализации показан на фиг. 2.

1. Система релятивистского квантового распределения ключей, работающая по атмосферному каналу, содержащая источник ослабленного излучения, по крайней мере один интерферометр задержки и однофотонный детектор, измеряющий результат интерференции в интерферометре, отличающаяся тем, что приемный интерферометр задержки корректируется по фазе с помощью Байесовского статистического метода, основанного на использовании однофотонного фотодетектора в качестве источника сигнала ошибки.

2. Система по п. 1, отличающаяся тем, что корректировка фазы интерферометра происходит однократно перед каждым сеансом распределения ключей.

3. Система по п. 1, отличающаяся тем, что корректировка фазы интерферометра происходит непрерывно во временных промежутках между квантовыми посылками для распределения ключей.

4. Система по п. 1, отличающаяся тем, что Байесовская статистическая модель для нахождения текущей фазовой ошибки интерферометра учитывает случайные медленные флуктуации фазы интерферометра.

5. Система по п. 1, отличающаяся тем, что используется адаптивный Байесовский алгоритм нахождения текущей фазовой ошибки интерферометра.