Комбинационный сумматор

Комбинационный сумматор

Иллюстрации

Показать все

Реферат

 

;=„МБА

Союз Советских

Социалистических

Реслублик

К АВТОРСКОМУ СВИДЕТЕЛЬСТВУ (61) Дополнительное к авт. свид-ву (22) Заявлено 29.12.75 (21) 2305279/24 (51) М. Кл.2 б 06F 7/50 с присоединением заявки М

Государственный комитет

Совета Министров СССР (23) Приоритет ло делам изобретений Опубликовано 30.08.77. Бюллетень тче 32 (53) УДК 681.325.5 (088.8) и открытий

Дата опубликования описания 08.09.77 (72) Авторы изобретения

А. П. Стахов, В. А. Лужецкий и A. В. Оводенко

Таганрогский радиотехнический институт им. В. Д. Калмыкова (71) Заявитель (54) КОМБИНАЦИОННЫЙ СУММАТОР где

Таблица 1

Вес разряда

34 21 13 8

1 0 0

0 1 0 0

Нормальная форма числа 83

Изобретение относится к вычислительной технике и предназначено для параллельного суммирования многоразрядных двоичных чисел.

Известны параллельные комбинационные сумматоры с последовательным переносом, построенные на одноразрядных сумматорах и производящие суммирование чисел, представленных в обычной двоичной системе счисления (1).

Недостатком таких сумматоров является невозможность суммирования многоразрядных чисел, представленных в двоичной «фибоначчиевой» позиционной системе счисления (2).

В этой системе счисления любое натуральное число представляется в виде многочлена

N = ар (l) + ат т Р (1 — 1) + ат ят (! — 2) +

+... + а,р (О), (1) 0 при i(0 (i) = 1 при т =0 р (т — 1) + р (i — 2) при т .> 0; а,=О; 1.

Представление (1) называется нормальной формой представления, если оно получено пу10 тем разложения N и всех возникающих в процессе такого разложения остатков r, по формуле

Л" = V(i+1)+ri

15 где V(i+1) и V(i) задаются соотношением (2).

Для нормальной формы представления чисел в «фибоначчиевой» системе счисления характерно наличие не менее одного нуля после каждой единицы. Например, нормальная фор20 ма числа 83 имеет вид, показанный в табл. 1.

570896

Сложение двух цифр одноименных разрядов в двоичной «фибоначчиевой» системе счисления выполняется следующим образом:

0+0= О

0+1=1

1+0= 1

1+1 = 1001.

Если в данном разряде слагаемых есть две единицы, то в «фибоначчиевой» двоичной системе счисления, в отличие от традиционной двоичной системы счисления, наряду с переносом в следующий старший разряд имеется еще перенос в младший разряд, отстоящий от данного на два разряда, что вытекает из рекуррентного соотношения (2), y (l) + cp (l) = cp (I) + cy {l — 1) + cp (l — 2) =

= (+ 1) + V { — 2)

Отсюда следует, что при сложении двух многоразрядных двоичных чисел, представленных в нормальной форме, возможна ситуация, когда в один разряд происходит два переноса: один со стороны предыдущего младшего разряда слагаемых, другой — со стороны старшего, отстоящего от данного на два разряда.

Следовательно, одноразрядный двоичный

«фибоначчиевый» комбинационный сумматор должен содержать четыре входа: два входа для цифр данного разряда слагаемых и два входа для цифр указанных переносов.

Благодаря нормальной форме представления слагаемых невозможно поступление двух переносов в любой разряд, когда оба слагаемых этого разряда равны единице, т. е. на входы одноразрядного сумматора не может подаваться, в любом случае, одновременно более трех единичных сигналов.

Практическая полезность «фибоначчиевой» системы счисления состоит в увеличении ошибкообнаруживающей способности и в возможности диагностики сумматора.

Ближайшим аналогом изобретения можно считать, например, комбинационный сумматор, содержащий в каждом разряде одноразрядные сумматоры, выходы суммы которых являются выходами разрядов сумматора (3).

Недостатком такого сумматора является невозможность суммирования многоразрядных чисел, представленных в двоичной «фиббоначчиевой» системе счисления.

Цель изобретения — расширение функциональных возможностей комбинационного сумматора, заключающееся в выполнении дополнительной функции суммирования многоразрядных чисел, представленных в двоичной

«фибоначчиевой» системе счисления при сохранении функции суммирования многоразрядных двоичных чисел, представленных в традиционной двоичной системе счисления.

Это достигается тем, что каждый i-й (i = 1, 2, ..., n) разряд сумматора дополнительно содержит логический узел и элемент И, шины

i-х разрядов слагаемых подключены к перво5

З0

65 му и второму входам логического узла соответствующего i-го разряда сумматора, третий вход логического узла i-го разряда — к выходу переноса одноразрядного сумматора (i — 1)-ro разряда, а четвертый вход — к выходу элемента И соответствующего i-го разряда сумматора. Первый вход элемента И i-го разряда соединен с выходом переноса одноразрядного сумматора (i+2) -ro разряда, а второй — с шиной управления. Выходы логического узла i-го разряда подсоединен к входам одноразрядного сумматора соответствующего i-ro разряда, выход переноса одноразрядного сумматора i-го разряда — к третьему входу логического узла (i+1) -го разряда и второму входу элемента И (i — 2) -го разряда.

Логический узел каждого разряда содержит два элемента И и три элемента ИЛИ, Первый вход логического узла соединен с первыми входами первых элементов И и ИЛИ, вторые входы которых связаны с вторым входом логического узла, третий вход логического узла — с первыми входами вторых элементов И и ИЛИ, вторые входы которых соединены с четвертым входом логического узла. Выходы элементов И подключены к входам третьего элемента ИЛИ, выходы элементов ИЛИ являются выходами логического узла.

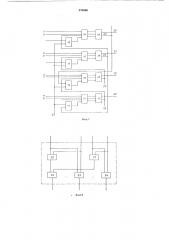
На фиг. 1 представлена схема четырех разрядов комбинационного сумматора; на фиг, 2— схема логического узла.

Сумматор содержит шины (входы) 1 — 4 первого слагаемого, шины (входы) 5 — 8 второго слагаемого, шину (вход 9) управления; элементы И 10 — 13 (i+2)-го, (i+1)-го, i-го, (i — 1)-ro разрядов соответственно; логические узлы 14 — 17 (i+2)-го, (i+1)-го, ко, (i — 1)-ro разрядов соответственно, одноразрядные (комбинационные) сумматоры 18 — 21 (i+2) -го, (i+1) -го, i-го, (i — 1) -го разрядов соответственно, выходы 22 — 25 переноса, выходы 26 — 29 суммы.

Логический узел включает в себя элементы

И 30 и 31, элементы ИЛИ 32, 33 и 34.

При сложении чисел, представленных в «фибоначчиевой» системе счисления в нормальной форме, сигналы соответствующих разрядов слагаемых поступают на входы 1 — 8.

На управляющий вход 9, связанный с первыми входами элементов И 10 — 13, подается единичный сигнал, разрешающий прохождение сигналов с выходов 22 — 25 пере носа со стороны старших суммируемых разрядов через элементы И 10 — 13 на один из входов логических узлов 14 — 17. На другие входы логических узлов поступают сигналы слагаемых соответствующего разряда и сигналы переноса со стороны младших разрядов.

Каждый логический узел 14 — 17 осуществляет распределение сигналов, поступающих на его входы, между тремя входами соответствующего одноразрядного комбинационного сумматора, потому что при сложении чисел, представленных в «фибоначчиевой» системе счисления, из четырех входных сигналов ло570896

Таблица 2

Десятичный эквивалент 21 13 8 5 3 2 1 1

1-е слагаемое

2-е слагаемое

О 1 О 0 1 О 1 О

О 1 0 О 1 О 1 О

1 I

1

t / 1

1 О 1 О 1 О 1 1

0 1 О 1 О 1 0 0

Сумма

1-е слагаемое

2-е слагаемое

0 1 0 1 О 1 0 О

20

Сумма

1 О 1 1 1 1 О 1

Введение дополнительных элементов и связей позволяет дополнительно производить операцию суммирования многоразрядных двоичных чисел, представленных в двоичной «фибоначчиевой» системе счисления, которая обладает способностью обнаруживать искажения двоичных комбинаций. гического блока единичное значение могут принимать одновременно не более трех сигналов.

При сложении чисел, представленных в традиционной двоичной системе счисления, на управляющий вход 9 подается нулевой сигнал, запрещающий прохождение через элементы И

10 — 13 на вход логических узлов сигналов переноса со стороны старших суммируемых разрядов.

На выходах 26 — 29 формируются сигналы результата суммирования двух чисел, представленных как в двоичной, так и в «фибоначчиевой» системах счисления.

Примеры сложения многоразрядных чисел в

«фибоначчиевой» системе счисления приведены в табл. 2 (здесь стрелками указаны переносы).

Формула изобретения

1. Комбинационный сумматор, содержащий в каждом разряде одноразрядные сумматоры, выходы суммы которых являются выходами разрядов сумматора, отличающийся тем, что, с целью расширения функциональных возможностей, каждый г-й (i=1, 2, ..., n) разряд сумматора дополнительно содержит логический узел и элемент И, шины i-х разрядов слагаемых подключены к первому и второму входам логического узла соответствующего i-го разряда сумматора, третий вход логического узла i-го разряда подключен к выходу переноса одноразрядного сумматора (1 — 1)-го разряда, а четвертый вход — к выходу элемента И соответствующего i-го разряда сумматора, первый вход элемента И i-го разряда соединен с выходом переноса одноразрядного сумматора (i+2)-го разряда, а второй — с шиной управления, выходы логического узла i-го разряда соединены с входами одноразрядного сумматора соответствующего i-го разряда, выход переноса одноразрядного сумматора i-го разряда подключен к третьему входу логического узла (i+1)-го разряда и второму входу элемента И (i — 2) -ro разряда.

2. Сумматор по и. 1, отл ич а ющпйся тсм. nто логический узел каждого разряда содержит два элемента И и три элемента ИЛИ, причем первый вход логического узла соединен с первыми входами первы.;. элементов И и

ИЛИ, вторые входы которых соединены с вторым входом логического узла, третий входкоторого подключен к первым входам вторых элементов И или ИЛИ, вторые входы которых соединены с четвертым входом логического узла, выходы элементов И подключены к входам третьего элемента ИЛИ, выходы элемен40 тов ИЛИ являются выходами логического узла.

Источники информации, принятые во внимание при экспертизе

1. Карцев М. А. Арифметика цифровых ма45 шип. М., «Наука», 1969, с. 142, рпс. 2.1.

2. Однородные цифровые вычислительные и интегрирующие структуры, вып. 2, Таганрог, 1974, с. 5 — 41.

3. Букреев И. Н. и др. Микроэлектронные

50 схемы цифровых устройств. М., «Сов. радио», 1975, с. 329, рис. 8.7,