Прибор для умножения и деления многозначных чисел на однозначные

Прибор для умножения и деления многозначных чисел на однозначные

Иллюстрации

Показать все

Реферат

 

№ 900

Класс 42п1

ПАТЕНТ НА ИЗОБРЕТЕНИЕ

О П И СА Н И Е прибора для умножения и деления многозначных чисел на однозначные.

К патенту А. А. Зернова, заявленному 14 апреля 1923 года (заяв. свид. № 76568).

0 выдаче патента опубликовано 30 января 1926 r. Действие патента распространяется на 15 лет от 15 сентября 1924 г.

Предлагаемый счетчик представляет собою соединение брусков для умножения Женайля и Люкаса, опубликованных в 1885 r., и численника для умножения и деления многозначных чисел

И. А. Григоровича, вышедшего в 1901 r., и имеет целью дать портативный и удобный в обращении счетчик, сводя щий умножение многозначных чисел на однозначные (а следовательно облегчающий и действие деления) к простому списыванию ряда цифр без какихлибо арифметических действий.

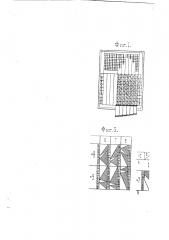
На фиг. 1 изображен численник Григоровича, на котором отложено множимое 148750, на фиг. 2 изображены части бруска Женайля и палочки Непера для множимого 7, на фиг. 3 изображены части брусков Женайля для умножения 672 на множители 8 и 9, на фиг. 4 изображено для сравнения умножение 148750 = 1041250 при помощи палочек Непера и при помощи предлагаемого счетчика, и на фиг. 5 изображен счетчик для множимого в восемь цифр, Численник Григоровича представляет собою обычные палочки Непера, но выполненные не брусками, требующими подборки и укладки для каждого числа,. с которым производится действие, а следующим способом:

Числа палочек Непера отпечатаны на полосках хорошего гибкого картона и подобраны пачками так, что сверху находится полоска с числами. произведений 0 на 1, 2, 3....9; под ней с числами произведений 1 на 1, 2, 3... ...9; 2 на 1,2.3,...9 ит.д. до 9 на 1, 2, 3,.... 9. Таких палочек, прикрепленных нижними концами к переплету численника, имеется столько, на сколько цифр множимого сделан численник. Верхние концы полосок выдаются один из-под другого и на них указаны цифры, являющиеся множимыми (О, 1, 2,....9); с правой и левой сторон на переплете счетчика помещены однозначные множители в порядке сверху вниз

1, 2,... 9. Таким образом, численник имеет вид, изображенный на фиг. 1, где на нем отложено множимое число

148750, т. е. отогнуты соответствующие полоски. Для получения произведений этого числа, надо выписывать из горизонтального ряда, соответствующего множителю, справа налево цифры, производя сложение цифр одинаковых разрядов. Так, например, произведения

148750 на 7 будет (справа налево): l

0 единиц, 5 десятков (9 + 3 — 10) =

= 2 сотни, (6+ 4+ 1 10) = 1 тысяча, (8+5+1 — 10) =4 десятка тысяч, (7+ 2+1 — 10) = 0 сотен + i

+ 1 миллион, т. е. 1.041.250, Автор считает работу с таким численником утомительной и полагает, что, взяв внешнее выполнение счетчика по типу упомянутого численника, необходимо изменить его содержание.

Автор брусков, Женайль, обратил внимание на то, что при перемножении любого однозначного числа на однозначные, количество могущих получиться единиц следующего разряда не может быть больше количества единиц в множимом без одной. Поэтому, при умножении двузначного числа на однознач- 1 ное число в, к цифре десятков произ- I ведения, получающегося от умножения на в десятков множимого, может прибавиться от перемножения единиц ияи

1 десяток, или 2, или 3 и т. д, до (в — 1) десятков. Вследствие этого, можно к цифрам низшего разряда палочек Непера приписать ряд цифр, которые могут получиться вследствие добавки от умножения цифры предыду-,, щего разряда на взятый множитель., При этом получится для строки, соот- ветствующей множителю 2 — две цифры,, для строки, соответствующей множи- телю 3 — три цифры и т. д. На фиг. 2; изображены части бруска Женайля и палочки Непера для множимого 7.

Имея заполненные таким образом бруски, остается только найти способ узнавать, какую же из возможных цифр произве-, дения следует брать. Достигается это, простыми указателями. Рассматривая каждое из частных произведений, можно заметить, что к цифре следующего разряда произведения может прибавиться только или количество десятков, получаемое при перемножении множителей (т. е. цифры данного бруска на мно- жителя соответств. строки) или на еди- ницу больше. Женайль применял указатели в виде треугольников, захватывающих основанием те цифры бруска, при которых получается одинаковая прибавка, а вершиной указывающих на соответствуюшую строку следующего (левого) бруска. На фиг. 3 изображена часть брусков Женайля для умножения

672 на множители 8 и 9. Умножение

672 >< 8 производится, следовательно, так:

Выписывается цифра единиц, равная 6 (верхняя цифра соответств. горизонтальной серии правого бруска); вершина соответствующего этой цифре треугольника указывает цифру десятков=7; вершина треугольника, в основании коего включена эта цифра, указывает цифру сотен =3 и вершина треугольника, соответствующего 3 — указывает цифру тысяч — 5. Имеется, следовательно, 672 X 7= 5376. Умножение

672 Р9 дает таким же способом 6048.

То, что Женайль располагает на неудобных в обращении брусках, можно расположить на полосках картона, подобных примененным в численнике Григоровича, что и даст в общем предлагаемый счетчик. Для устранения некоторых неудобств в обращении, имеющих место в численнике Григоровича, полоски удлинены на нижнем конце так, чтобы при умножении на 8 и 9 не приходилось слишком сильно отгибать их, чтобы увидеть соответствующие строки счетчика. Изменены также указатели: вместо треугольников взяты трапеции, причем одна из них черная, а другая белая и с левой стороны полосок нанесены черточки высшего разряда; благодаря этому, картина пути, которым надо следовать при списывании цифр, получается более наглядной.

В целях той же большей наглядности, цифры, соответствующие множителю 1, взяты значительно более крупного размера и поставлены посередине полосок, так как после отгиба полосок цифры эти дают множимое, что служит для контроля правильности его установки (подобно первому повороту ручки арифмометра). Верхние цифры групп цифр, соответствующих каждому множителю, также взяты крупнее остальных (или могут быть подчеркнуты, напечатаны другим шрифтом, цветом и т.п.), так как этими цифрами (крайнего правого бруска) начинается списывание произведения — при списывании справа налево, или этими цифрами произведение должно окончиться — при списывании слева направо. На фиг. 4 изображено, для сравнения, умножение

148750X7=1041250 при помощи палочек Непера и при помощи предлагаемого счетчика. На фиг. 5 представлен в натуральную величину счетчик для множимого в 8 цифр (что соответствует обычному а рифмометру). При таком количестве цифр ширина счетчика равна 110 — 115 мм., т. е. не превосходит ширины бумажника (размеры могут быть и еще уменьшены).

Высота каждой строки равна 3 мм., что позволяет поместить на ней свободно

2 - х - милиметровую цифру обычного шрифта логарифмических таблиц (напр., Вега),, математических таблиц Хютте и т. п.

По желанию, счетчик может быть сделан на любое количество цифр множимого и, вообще, любого размера.

Счетчик может выполняться в виде книги, раскрывающейся обычным порядком или вверх †виде блокнота и т. п. Равно и полоски могут откидываться вниз или вверх.

ЛРЕдМЕТ IIATEHTA.

Прибор для умножения и деления многозначных чисел на однозначные, отличающийся применением численника, состоящего из подобранных пачками, по десяти штук, полосок гибкого картона, прикрепленных в произвольном количестве нижними своими концами к переплету и имеющих верхние концы, выдающиеся один из-под другого и снабженные цифрами от 0 до 9, на каковые полоски против однозначных цифр от 0 до 9, стоящих с правой и левой их сторон на переплете, нанесены цифры и трапецоидальные указатели различной окраски.