Способ создания независимых многомерных градуировочных моделей
Иллюстрации
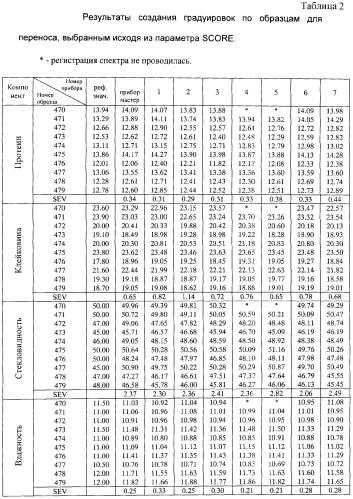
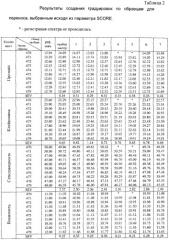
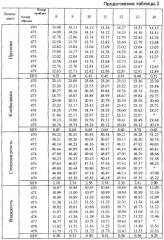
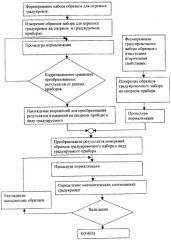
Показать всеИзобретение относится в аналитическому приборостроению, в частности к способам создания градуировочных моделей для различного вида измерительных приборов, позволяющих определить одно или несколько вторичных свойств неизвестного образца по результатам измерения множества первичных свойств этого образца. Способ создания независимых многомерных градуировочных моделей включает в себя подбор градуировочного набора образцов с известными вторичными свойствами, измерение на опорном приборе первичных свойств каждого из образцов градуировочного набора. Затем способ предусматривает преобразование с помощью соотношений переноса градуировок результатов измерения первичных свойств образцов градуировочного набора на опорном приборе к виду, эквивалентному результатам измерения образцов градуировочного набора на градуируемом приборе. Далее осуществляется сопоставление преобразованных к виду, эквивалентному результатам измерения на градуируемом приборе, результатов измерений первичных свойств образцов градуировочного набора с известными вторичными свойствами этих образцов и создание при помощи методов регрессионного анализа независимой многомерной градуировочной модели, выражающей вторичные свойства образцов через измеренные на градуируемом приборе первичные свойства. Математические соотношения переноса градуировок определяют, подбирая набор образцов для переноса градуировок, измеряя первичные свойства каждого образца из набора для переноса градуировок на опорном и градуируемом приборах и сопоставляя при помощи методов многомерного регрессионного анализа результаты измерений первичных свойств образцов набора для переноса градуировок, полученные на опорном приборе, с результатами измерения первичных свойств тех же самых образцов, полученными на градуируемом приборе. Выбор независимой многомерной градуировочной модели производят с использованием количественных параметров валидации градуировки. Способ обеспечивает высокую точность предсказания свойств неизвестного образца, высокую точность определения анализируемых свойств и учитывает нелинейные отличия технических параметров градуируемого и опорного приборов и влияние условий эксплуатации. 11 з.п. ф-лы, 1 ил., 2 табл.
Реферат
Заявляемое изобретение относится к аналитическому приборостроению. В частности, изобретение относится к способам создания градуировочных моделей для различного вида измерительных приборов, позволяющих определить одно или несколько вторичных свойств неизвестного образца по результатам измерения множества первичных свойств этого образца.
В различных отраслях промышленности и научных исследований возникает задача определения одного или одновременно нескольких свойств образцов, например октанового числа бензина или содержания протеина, влаги и золы в зерне пшеницы. Причем при определении свойств образцов существенными являются такие характеристики метода измерения, как скорость проведения анализа и сохранение образцов в процессе измерений. Это особенно важно для промышленных применений, где стремятся иметь быстрый неразрушающий контроль свойств продукции на разных стадиях производства.
Очень часто определение свойств образца при помощи прямых методов измерения не обеспечивает необходимой скорости анализа или приводит к разрушению образца. Типичным примером является задача аналитической химии по определению концентраций образующих образец компонентов, где традиционный прямой метод химического анализа основан на проведении химических реакций, что приводит к разрушению образца, а, кроме того, требуется значительное время для проведения анализа. Поэтому для решения проблемы быстрого неразрушающего анализа свойств образцов был разработан целый ряд непрямых методов, где анализируемые свойства образцов определяют путем измерения других свойств образцов, зависящих от анализируемых свойств, которые, однако, в отличие от анализируемых свойств могут быть легко измерены напрямую в течение короткого промежутка времени и без разрушения образца. Часто измеряемые свойства образцов называют «первичными свойствами», а анализируемые свойства образцов, от которых зависят результаты измерений, но которые не измеряются непосредственно, называют «вторичными свойствами». Одним из наиболее эффективных непрямых методов исследования является спектроскопический анализ, при котором "вторичные" свойства образцов (например, химический состав) определяются по результатам измерений их спектральных характеристик, таких как оптические спектры поглощения, отражения или рассеяния, выступающие в качестве "первичных" свойств.
Для любого непрямого метода анализа свойств образцов очень важным является этап определения математических соотношений между результатами измерений первичных свойств образца и значениями величин, характеризующих анализируемые вторичные свойства. Эти соотношения между измеряемыми на приборе первичными характеристиками и анализируемыми вторичными свойствами образца называются градуировочными моделями или просто градуировками.
Создание градуировочных моделей является одной из главных задач при использовании непрямых методов исследования. Процесс этот достаточно долгий и трудоемкий, особенно для случая так называемого многомерного анализа, когда для определения количественных характеристик вторичных свойств образца используется набор результатов измерения большого числа параметров, характеризующих первичные свойства. Например, в случае спектроскопического анализа для определения концентрации различных компонентов проводят измерения большого количества спектральных данных (величины поглощения, отражения или рассеяния) для разных значений волновых чисел (длин волн, частот).
Для построения градуировочной модели, дающей заданную точность определения параметров, характеризующих анализируемые вторичные свойства произвольного образца, необходимо провести анализ большого набора образцов, похожих на образцы, которые будут анализироваться на приборе в дальнейшем (градуировочный набор). Подбор образцов градуировочного набора строго регламентируется стандартами на различные непрямые методы анализа, например стандартом на качественный анализ при помощи БИК спектроскопии [1]. Образцы градуировочного набора должны иметь известные значения параметров, характеризующих анализируемые вторичные свойства, которые определяются при помощи прямого референтного метода, имеющего заданную точность и воспроизводимость. В рассмотренном ранее примере по спектроскопическому анализу химического состава образцов анализируемые свойства образцов градуировочного набора могут быть предварительно определены стандартными химическими методами с использованием химических реакций. Диапазон изменения вторичных свойств образцов градуировочного набора должен полностью покрывать диапазон возможных изменений этих свойств при анализе неизвестных образцов. Кроме того, для создания наиболее устойчивой модели образцы в градуировочном наборе должны быть однородно распределены в диапазоне изменения анализируемых свойств.
Окончательные выводы о правильности подбора образцов градуировочного набора и устойчивости построенной по нему градуировочной модели могут быть сделаны только после стандартной процедуры валидации градуировочной модели [1], оценки числа степеней свободы и определения выпадающих из градуировки образцов. Вопрос об устойчивости градуировочной модели является очень важным, так как определяет область применимости построенной градуировки. В случае неустойчивой градуировочной модели небольшие шумовые изменения в измеряемых первичных свойствах могут привести к статистически значимым изменениям в результатах анализа вторичных свойств. Повышение устойчивости градуировочной модели осуществляется путем исключения из градуировочного набора образцов с выбросами в характеристиках. Поиск таких образцов осуществляется на основании статистического анализа выбросов, например по расстоянию Махаланобиса [1], использующего данные измерений первичных свойств полного градуировочного набора.
Другой важный вопрос, возникающий при использовании градуировочной модели для определения вторичных свойств неизвестного образца - это оценка того, насколько точно построенная модель описывает данный образец и обеспечивает необходимую точность определения его вторичных свойств. Измеренные первичные свойства образца также подвергают анализу по статистике определения выбросов. Критерием применимости градуировочной модели для анализа свойств неизвестного образца может являться вычисленное для данного образца расстояние Махаланобиса. Проблема применимости градуировочной модели для описания неизвестного образца перекликается с задачами, решаемыми при качественном анализе, где на основании измерения первичных свойств образца (спектральных данных) и сопоставления их с библиотечными данными делается вывод о наборе компонентов в образце. Отметим, что для определения расстояния Махаланобиса необходимо иметь полную информацию о результатах измерений первичных характеристик всех образцов градуировочного набора, причем условия измерений анализируемого образца и градуировочных образцов должны быть идентичными.
На результаты измерения первичных свойств образцов, а как следствие, и на точность определения параметров, характеризующих анализируемые вторичные свойства образцов, могут существенно влиять изменения внешних условий, а также технические характеристики измерительного прибора. Поэтому было предложено несколько способов создания градуировочных моделей, мало восприимчивых к изменению условий измерений, а также несколько способов переноса градуировочных моделей между измерительными приборами, что позволяет учесть различия в технических характеристиках приборов и не повторять сложный процесс построения градуировочной модели на каждом отдельном приборе.
Известен способ создания многомерных градуировочных моделей [2, 3], обладающих малой восприимчивостью к изменению параметров прибора, на котором проходят измерения, а также к изменению внешних условий, при которых происходят измерения, и к изменению прочих свойств образца. В данном способе для создания градуировочной модели проводят измерение большого числа параметров, характеризующих первичные свойства образца, для каждого образца из так называемого градуировочного набора образцов с известными вторичными свойствами. Образцы градуировочного набора выбираются таким образом, чтобы прочие свойства образцов изменялись в максимально возможном диапазоне. Кроме того, при измерении первичных свойств образцов из градуирочного набора намеренно производят изменения параметров измерительного прибора, на котором проводят построение градуировочной модели, например, в случае спектрометров вводят спектральные искажения и изменение амплитуды измеряемого сигнала. Величина изменения параметров прибора при построении градуировочной модели определяется максимально возможными величинами изменения этих параметров, которые ожидаются между различными приборами при производстве или будут возникать в процессе эксплуатации. Дополнительно вводят изменение внешних условий. Изменения параметров прибора или других условий измерений могут также вводиться не в процессе проведения реальных измерений, а путем математических преобразований.
Данный способ позволяет создать многомерную градуировочную модель, дающую результаты анализа вторичных свойств образца, мало зависящие от условий измерений и прибора, на котором эти измерения происходили, поэтому градуировочная модель создается один раз и используется без изменений на всех однотипных приборах. Намеренное введение разброса данных результатов измерения образцов градуировочного набора безусловно делает модель более устойчивой, а область применимости построенной данным способом градуировки более широкой.
Однако точность результатов анализа с использованием градуировочной модели, созданной по данному способу, будет снижена, т.к. в модели изначально предполагается вариация результатов измерения первичных свойств. Кроме того, число факторов, влияющих на результаты измерений, очень большое и не всегда возможно построение математической модели, учитывающей влияние всех возможных факторов. Поэтому для построения полноценной градуировочной модели, учитывающей влияние большого количества дополнительных факторов, необходимо провести огромный объем измерений образцов градуировочного набора при различных условиях, что делает и без того сложный процесс создания градуировочной модели еще более трудоемким и долгим. Последним недостатком градуировочной модели, созданной при помощи данного метода, является то, что введение вариаций в результаты измерений образцов градуировочного набора затрудняет оценку правомерности применения градуировочной модели для анализа того или иного неизвестного образца, что может привести к ошибкам в анализе вторичных свойств. Например, может оказаться так, что градуировочная модель для определения процентного содержания различных химических компонентов в образце будет использована для анализа неизвестного образца, состоящего из других компонентов, в значительной степени отличающегося от образцов градуировочного набора.
Существует другой подход к созданию многомерных градуировочных моделей, при котором не пытаются построить универсальную градуировочную модель, работающую на всех приборах и учитывающую все возможные факторы, влияющие на результаты измерений. Вместо этого, для того чтобы градуровочная модель, построенная на одном приборе, работающем при одних условиях, позволяла определять вторичные свойства образцов по результатам измерений первичных свойств на другом измерительном приборе, который отличается по техническим параметрам и работает в других условиях, используют специально разработанные способы переноса градуировок.
J. Shenk и др. [4] предложили способ переноса многомерной градуировочной модели между спектрометрами, основанный на преобразовании спектральных данных, измеренных на градуируемом приборе, к виду, эквивалентному измерениям на опорном приборе, использовавшемся для создания градуировочной модели. Определение вторичных свойств неизвестных образцов проводят после преобразования спектральных данных, напрямую используя созданную на опорном приборе градуировочную модель.
Изначально градуировочная модель создается на опорном спектрометре с использованием методов многомерного регрессионного анализ (таких, как многолинейная регрессия MLR, регрессия основных компонентов PCR или метод дробных наименьших квадратов PLS), при помощи которых находят соотношения, связывающие известные значения параметров, описывающих анализируемые вторичные свойства образцов из градуировочного набора с измеренными на опорном приборе спектральными характеристика этих образцов (например, со спектрами поглощения). Для переноса градуировочной модели на градуируемый прибор используется набор образцов для переноса градуировок также с известными анализируемыми свойствами; например, это может быть часть образцов из градуировочного набора. Спектральные характеристики образцов из набора для переноса градуировок измеряются как на опорном, так и на и градуируемом приборах. После чего путем сопоставления результатов измерений спектральных характеристик одних и тех же образцов на опорном и градуируемом спектрометрах находят математические соотношения, позволяющие преобразовать спектральные данные, измеренные на градуируемом приборе, к виду, эквивалентному результатам измерений на опорном приборе. Найденные математические соотношения каждый раз используют для выполнения преобразований над результатами измерений спектральных характеристик неизвестного образца на градуируемом приборе. После чего градуировочная модель, созданная на опорном спектрометре, может быть применена для определения вторичных свойств неизвестного образца.
Более детально процедура поиска математических соотношений для преобразования спектральных данных выглядит следующим образом. На первом шаге определяют сдвиг волновых чисел. Для определения сдвига волновых чисел вычисляются корреляционные коэффициенты между спектральными данными, измеренными на опорном приборе при заданном волновом числе со спектральными данными, измеренными на градуируемом приборе при нескольких ближайших к заданному значениях волновых чисел. Далее делается предположение, что корреляционные коэффициенты связаны квадратичной зависимостью со значениями волновых чисел в спектральных данных, измеренных на градуируемом приборе. Коэффициенты данной квадратичной зависимости определяются методом наименьших квадратов. Значение волнового числа градуируемого прибора, при котором достигается максимум квадратичной зависимости, соответствует заданному значению волнового числа опорного прибора, откуда определяем спектральный сдвиг для каждой точки в спектральных данных опорного прибора. Такая процедура нахождения спектрального сдвига хорошо работает для приборов со сканирующей дифракционной решеткой в силу их конструктивных особенностей.
После определения спектрального сдвига проводят процедуру линейной интерполяции спектральных данных, измеренных на градуируемом приборе, где находят значения амплитуды измеряемого сигнала при заданных значениях волновых чисел, соответствующих значениям волновых чисел в опорных спектральных данных. Далее проводят амплитудную корректировку интерполированных спектральных данных, находя методом наименьших квадратов коэффициенты линейной связи между интерполированными спектральными данными и опорными спектральными данными. При некоторых значениях волновых чисел невозможно найти корректирующие коэффициенты, поскольку значение спектральных данных в этих точках равно нулю, это может быть результатом математической предобработки исходных результатов измерений, например дифференцирования спектральных данных; в этом случае корректирующие амплитудные коэффициенты для этих волновых чисел находятся путем интерполяции.
Таким образом, результатом данного способа переноса градуировок являются: созданная на опорном приборе градуировочная модель и данные, необходимые для выполнения преобразования результатов измерения спектральных характеристик на градуируемом приборе к виду, эквивалентному измерениям на опорном приборе, включающие величину спектрального сдвига и корректирующие амплитудные коэффициенты для каждого значения волнового числа.
Недостатками данного метода являются: узкая ориентированность на спектрометры со сканирующей дифракционной решеткой и большой объем вычислений, проводимый на градуируемом приборе при анализе неизвестного образца перед сопоставлением измеренных спектральных характеристик с градуировочной моделью для определения интересующих вторичных свойств. Это увеличивает время обработки данных и требует высоких вычислительных мощностей, что может оказаться существенным при анализе продукта непосредственно в процессе производства, где скорость получения данных является ключевым параметром. Помимо этого, в данном способе на градуируемом приборе не сохраняются данные о результатах измерений градуировочного набора, поэтому невозможно оценить применимость градуировочной модели для анализа неизвестного образца, что ограничивает область применения данного метода теми случаями, когда заранее известно, что неизвестный образец попадает в диапазон изменения спектральных данных, покрываемый градуировочным набором. Отсутствие данных о результатах измерения образцов градуировочного набора также не позволяет расширить градуировочную модель путем измерения дополнительных градуировочных образцов непосредственно на градуируемом приборе, так как для определения выпадающих из градуировочного набора образцов необходима полная информация о результатах измерений всех образцов градуировочного набора. Расширение градуировки без такой проверки может привести к неустойчивости градуировочной модели.
Наиболее полное описание методов переноса градуировочных моделей представлено в [5], где описано сразу несколько различных способов переноса градуировочных моделей. Хотя в данном патенте описываются способы переноса градуировок между спектрометрами, данные методы могут быть легко перенесены на любые другие приборы для анализа одного или нескольких вторичных свойств неизвестного образца по результатам измерения множества первичных свойств этого образца. В патенте рассмотрены три основных способа переноса градуировочных моделей с опорного прибора на градуируемый прибор. Как и в способе, предложенном в [4], изначально создается градуировочная модель, основанная на спектральных данных, измеренных на опорном приборе для градуировочного набора образцов с известными анализируемыми свойствами. Затем из градуировочного набора выбирается часть образцов и создается набор для переноса градуировок, который измеряется на градуируемом приборе, и используется для определения соотношений переноса градуировок. Для достоверного определения соотношений переноса градуировок образцы из набора для переноса градуировок должны обеспечивать достаточное количество информации об особенностях результатов измерений спектральных данных на разных приборах. Поэтому количество этих образцов должно быть не меньше ранга матрицы коэффициентов градуировочной модели, созданной на опорном приборе. Далее перенос градуировочной модели осуществляется путем сопоставления спектральных данных, измеренных на опорном и градуируемом приборе в соответствии с одним из предложенных способов.
В первом способе, названном авторами «классическим», предполагается, что для образцов из набора для переноса градуировок известны все анализируемые вторичные свойства, например концентрации составляющих образцы химических компонентов. Тогда связь между измеренными спектральными данными и известными свойствами образцов определяется двумя разными градуировочными моделями для опорного и градуируемого прибора, что может быть записано в матричной форме как.
где R1 - матрица спектральных данных, измеренных на опорном приборе, имеющая размерность m Х n; R2 - аналогичная матрица спектральных данных, измеренных на градуируемом приборе; n - число спектральных точек в результатах измерений, m - количество образцов в наборе для переноса градуировок, С - матрица определяемых свойств образцов (концентраций), имеющая размерность m Х с; с - число определяемых свойств; K1 - опорная калибровочная модель, К2 - скорректированная калибровочная модель, представленные в виде матриц коэффициентов, имеющие размерность с Х n. Матрица коэффициентов корректировки имеет вид
где C+ - псевдо или обобщенная обратная матрица свойств образцов (т.к. матрица С в общем случае неквадратная). Используя выражения (1) и (2), мы можем найти спектральные данные, которые были бы получены путем измерения всего градуировочного набора образцов на градуируемом приборе, после чего построить новую градуировочную модель. Таким образом, «классический» способ переноса градуировок использует известные свойства образцов из набора для переноса градуировок для того, чтобы определить корректирующие коэффициенты. Эти коэффициенты определяют связь между вторичными свойствами образцов из набора для переноса градуировок и измеряемыми на градуируемом приборе первичными свойствами этих образцов. После чего, исходя из известных вторичных свойств образцов полного градуировочного набора, используя данные коэффициенты корректировки, находят первичные свойства для каждого образца из полного градуировочного набора, эмулирующие измерения градуировочного набора на градуируемом приборе. Используя вычисленные значения первичных свойств образцов градуировочного набора и известные вторичные свойства этих образцов, при помощи методов регрессионного анализа создают новую градуировочную модель для градуируемого прибора, использующуюся в дальнейшем для определения вторичных свойств неизвестного образца по результатам измерения первичных свойств этого образца на градуируемом приборе.
Классический способ переноса градуировок возможно использовать только в том случае, когда точно известны все свойства образцов из градуировочного набора, например, есть точные данные о концентрации всех составляющих образец химических элементов. Кроме того, набор образцов для переноса градуировок - это часть образцов из полного градуировочного набора, для которых также должны быть известны все вторичные свойства. Кроме того, данный метод негласно предполагает, что скорректированная по набору для переноса градуировочная модель обладает достаточной точностью предсказания и устойчива, хотя реальной валидации не осуществляется. Как показывает опыт [5], для данного метода характерна относительно невысокая достоверность определения свойств образца.
В случае, когда нет необходимости в определении всех вторичных свойств образцов, а интересует лишь одно определенное свойство, например содержание белка, в [5] предложено использовать «обратный» способ переноса градуировок. Модифицированный "обратный" способ был также предложен в [6]. В этом способе объем математических вычислений значительно уменьшается по сравнению с «классическим» способом, т.к. матрица концентраций вырождается в вектор «с» размерности m и градуировочная модель также описывается вектором коэффициентов «b» размерности n. Сначала стандартным способом, используя многомерный регрессионный анализ, по градуировочному набору образцов создается градуировочная модель на опорном приборе, которая определяет соотношения, связывающие матрицу спектральных данных или других первичных свойств образцов из набора для переноса градуировок, измеренных на опорном приборе (R1), и определяемое вторичное свойство этих образцов.
Далее проводят измерения тех же самых образцов из набора для переноса градуировок на градуируемом приборе, причем коэффициенты градуировочной модели корректируются для получения известных значений характеристик, описывающих вторичные свойства образцов из набора для переноса градуировок.
В итоге, вектор коэффициентов новой градуировочной модели можно выразить через вектор коэффициентов опорной градуировочной модели и обратные матрицы результатов измерения первичных свойств (спектральных данных) образцов из набора для переноса градуировок на опорном и градуируемом приборах соответственно.
В отличие от «классического» способа переноса градуировок в "обратном" способе не проводится коррекция всех результатов измерения первичных свойств образцов градуировочного набора на опорном приборе с целью приведения их к виду, эквивалентному результатам измерения на градуируемом приборе. В этом методе на основании измерений образцов набора для переноса градуировок находятся скорректированные коэффициенты градуировочной модели, которые впоследствии используются для определения вторичных свойств неизвестного образца. Данный метод может быть расширен для случая, когда одновременно исследуются несколько свойств образца, тогда вектора будут заменены на матрицы.
Основное достоинство данного метода переноса градуировок в том, что для его реализации необходимы относительно невысокие вычислительные мощности. Причем результатом применения данного метода переноса градуировок являются скорректированные коэффициенты градуировочной модели, построенной на опорном приборе, которые напрямую используются для определения вторичных свойств по результатам измерения первичных свойств на градуируемом приборе, что существенно сокращает время анализа неизвестного образца.
Однако для достижения высокой точности определения свойств неизвестных образцов на градуируемом приборе необходимо использовать большое число образцов в наборе для переноса градуировок. Чем больше набор образцов, тем выше точность. Как и в "классическом" способе, в "обратном" способе нет возможности оценить применимость перенесенной градуировочной модели для анализа неизвестного образца, измеренного на градуируемом приборе, т.к. для этого необходимо иметь информацию о спектральных данных для всех образцов градуировочного набора, измеренных в условиях, эквивалентных условиям измерения неизвестного образца.
Третий способ переноса градуировок, описанный в [5], авторы назвали «прямым» способом. В этом способе, используя результаты измерения первичных свойств (спектральных характеристик) образцов из набора для переноса градуировок, полученные на опорном и градуируемом приборе, находят матрицу преобразования результатов измерения (F), определяющую функциональную связь между результатами измерения первичных свойств произвольного образца на опорном приборе и результатами измерения этого же образца на градуируемом приборе.
После чего первичные свойства произвольного образца, измеренные на градуируемом приборе, могут быть приведены к виду, эквивалентному результатам измерения этого образца на опорном приборе.
r2 - результаты измерения первичных свойств образца на градуируемом приборе, а r1' - результат математического преобразования результатов измерения первичных свойств образца на градуируемом приборе к виду, эквивалентному результатам измерения на опорном приборе.
В данном методе математические соотношения связывают каждое значение первичных свойств образца, преобразованных к виду, эквивалентному результатам измерения на опорном приборе, с каждым значением, измеренным на градуируемом приборе. Это означает, что каждая точка в спектральных данных, преобразованных к виду опорного прибора является функцией спектральных данных во всех точках, измеренных на градуируемом приборе. Это делает перенос градуировок наиболее точным, однако это также является причиной одного из недостатков данного способа. А именно того, что преобразование спектральных данных с использованием «прямого» метода требует высоких вычислительных мощностей и может существенно удорожать прибор. Число образцов в наборе для переноса градуировок должно быть равно, как минимум, рангу матрицы спектральных данных для полного градуировочного набора, измеренного на опорном приборе, а матрица преобразования результатов измерений, использующаяся в данном способе, имеет размерность n Х n, где n - число спектральных точек, в которых производят измерения, причем n, как правило, большое число и его значение может превышать 100. Кроме того, каждый раз перед определением анализируемых вторичных свойств образца необходимо провести математические преобразования измеренных данных к виду опорного прибора, что может значительно увеличить время анализа.
Отметим, что в описанном способе переноса градуировочных моделей при помощи тех или иных преобразований первичные свойства образцов, измеренные на градуируемом приборе, приводятся к виду, эквивалентному результатам измерения на опорном приборе, после чего для определения анализируемых вторичных свойств используется градуировочная модель, созданная на опорном приборе. Причем градуировочная модель, созданная на опорном приборе, должна пройти стандартную процедуру валидации [1], что гарантирует устойчивость модели, однако это не является достаточным условием того, что данная модель устойчива при анализе результатов измерений, полученных на градуируемом приборе и преобразованных к виду, эквивалентному результатам измерений на опорном приборе. Для этого результаты измерения неизвестного образца нужно проанализировать на присутствие выпадающих данных при помощи статистики предсказания выбросов, например статистики Махаланобиса, для чего необходима информация о результатах измерений образцов полного градуировочного набора, а не только данные о константах в математических соотношениях градуировочной модели. Поэтому в некоторых случаях полезно иметь отдельную "независимую" градуировочную модель. Под термином "независимая модель" мы подразумеваем такую градуировочную модель, которая создается отдельно для каждого градуируемого прибора, учитывает его особенности, дает возможность оценки применимости для анализа того или иного неизвестного образца и гарантирует устойчивость. Независимая градуировочная модель может быть расширена путем простого измерения дополнительных градуировочных образцов на градуируемом приборе без использования опорного прибора, например, для корректировки градуировочной модели при изменении параметров градуируемого прибора в процессе эксплуатации (старение).
Известен способ переноса градуировочных моделей между приборами [7], также ориентированный на перенос градуировок между спектрометрами. По совокупности существенных признаков данный способ является наиболее близким к заявляемому изобретению. Данный способ включает в себя: определение спектральной передаточной функции опорного и градуируемого спектрометров путем измерения спектральных данных на обоих приборах для монохроматического источника света; определение корреляционных соотношений между спектральными передаточными функциями опорного и градуируемого спектрометров и нахождение математических соотношений преобразования результатов измерений на опорном приборе к виду, эквивалентному результатам измерений на градуируемом приборе; подбор образцов градуировочного набора с известными анализируемыми свойствами; измерение на опорном спектрометре спектральных характеристик каждого образца из градуировочного набора; преобразование при помощи найденных соотношений спектроскопических данных для образцов градуировочного набора, измеренных на опорном спектрометре, к виду, эквивалентному результатам измерений образцов градуировочного набора на градуируемом спектрометре; и создание градуировочной модели для градуируемого спектрометра путем определения при помощи методов регрессионного анализа соотношений между известными свойствами образцов градуировочного набора и преобразованными спектральными данными.
Градуировочная модель, созданная на градуируемом приборе при помощи данного способа, является полностью не зависимой от опорного прибора. Причем данный способ дает возможность не повторять измерения образцов градуировочного набора на каждом градуируемом приборе, а использует преобразованные к виду градуируемого прибора данные, измеренные на опорном приборе. Такая градуировочная модель может быть легко дополнена и расширена путем измерения дополнительных градуировочных образцов непосредственно на градуируемом приборе.
Однако соотношения для преобразования результатов измерений, проведенных на опорном приборе, к виду, эквивалентному измерениям на градуируемом приборе, находятся путем сравнения откликов обоих приборов на один и тот же источник монохроматического света. Поэтому данный метод применим лишь для спектрометров и не может быть использован для приборов, использующих другие принципы анализа, когда другие неспектроскопические первичные свойства образцов измеряются. Отметим, что для получения достоверного переноса градуировок монохроматический источник должен обладать беспрецедентно высокой стабильностью. Такой источник излучения, как правило, имеет высокую стоимость и может быть не всегда доступен. Главным недостатком данного метода является то, что использование только одной монохроматической линии излучения не позволяет найти точные соотношения для преобразования спектральных данных. Теория спектральной передаточной функции разработана для линейного приближения. Однако очень часто вариации в характеристиках приборов имеют нелинейный характер, например сдвиг длины волны в приборах со сканирующей дифракционной решеткой [4]. Таким образом, использование математических преобразований, полученных данным способом, может привести к неверным результатам переноса спектральных данных в случае нелинейных изменений в характеристиках приборов. Кроме того, данный метод переноса градуировок не учитывает вариации в интенсивности и спектре излучения полихроматических источников света в самих градуируемых спектрометрах.
Техническим результатом изобретения является создание независимой градуировочной модели для определения одного или нескольких вторичных свойств неизвестного образца по результатам измерения множества первичных свойств этого образца, необязательно спектральных, которая обеспечивает высокую точность определения анализируемых свойств и учитывает нелинейные отличия технических параметров градуируемого и опорного приборов и влияние условий эксплуатации, а кроме того, дает возможность расширения и дополнения путем измерения дополнительных градуировочных образцов на градуируемом приборе.
Заявленный технический результат достигается в способе создания независимых многомерных градуировочных моделей, включающем в себя подбор градуировочного набора образцов с известными вторичными свойствами, измерение на опорном приборе первичных свойств каждого из образцов градуировочного набора, преобразование с помощью соотношений переноса градуировок результатов измерения первичных свойств образцов градуировочного набора на опорном приборе к виду, эквивалентному результатам измерения образцов градуировочного набора на градуируемом приборе, сопоставление преобразованных к виду, эквивалентному результатам измерений на градуируемом приборе, результатов измерений первичных свойств образцов градуировочного набора с известными вторичными свойствами этих образцов, и создание при помощи методов регрессионного анализа независимой многомерной градуировочной модели, выражающей вторичные свойства образцов чере