Способ автоматизированного разбиения на группы уровней яркости пикселов растровых изображений по значениям их повторяемости

Способ автоматизированного разбиения на группы уровней яркости пикселов растровых изображений по значениям их повторяемости

Иллюстрации

Показать все

Реферат

Изобретение относится к распознаванию растровых изображений и предназначено для увеличения эффективности определения пороговых значений яркости пикселов либо характеристик, производных от них для заданных матриц растровых изображений. При пороговых методах используется тот факт, что пикселы, формирующие изображения отдельных объектов изображения, имеют близкие уровни яркости и они занимают довольно большие участки общей площади изображения. Поэтому решение при отнесении пиксела к тому или иному объекту изображения может быть принято на основании сравнения анализа его яркости с некоторым пороговым значением.

Известны системы распознавания, например, при сканировании изображений, в которых пороги задаются вручную, например в системах сканирования фирмы EPSON [1]. Данные методы требуют обязательное участие человека в предварительном анализе изображения и не применимы в системах автоматического распознавания.

Наиболее близким по совокупности признаков является способ разбиения на группы (критерий развала на кучи), предложенный в работе [2]. Здесь рассмотрена некоторая числовая характеристика s, которая может принимать n различных значений s_i(i=1,...,n), имеющих значения повторяемости, задаваемые гистограммой Н={h₁,...,h_n}. Определен общий объем совокупности чисел

и ее дисперсия При помощи порогов совокупность чисел s разбита на кучи {s¹,...,s^N} из подряд стоящих значений чисел. Для каждой кучи s^u рассмотрен объем Q^u и дисперсия σ^u2. Показатель кучности задан формулой

В качестве лучшего принимается разбиение с наименьшим значением показателя κ. При отсутствии ограничений для любой гистограммы Н глобальный минимум показателя κ=0 будет достигаться на тривиальном разбиении на кучи, при котором каждая куча состоит только из одного числа s_i. Однако такой глобальный минимум не дает конструктивной информации по разделению изображения. Поэтому предложено на область поиска наложить дополнительные ограничения: 1) вначале группы s^u _н идет возрастание значений повторяемости, а в конце s^u _к - их убывание, 2) объем каждой кучи не должен быть слишком малым (Q^u/Q≥1/8), 3) число куч не должно быть больше 4 (N≤4).

Предложенный способ обладает следующими недостатками.

1. При возрастании N величина критерия κ как правило также возрастает. Это не позволяет сравнивать пороговые разбиения с различными значениями N. Данный критерий позволяет сравнивать между собой разбиения с одинаковыми количествами групп N.

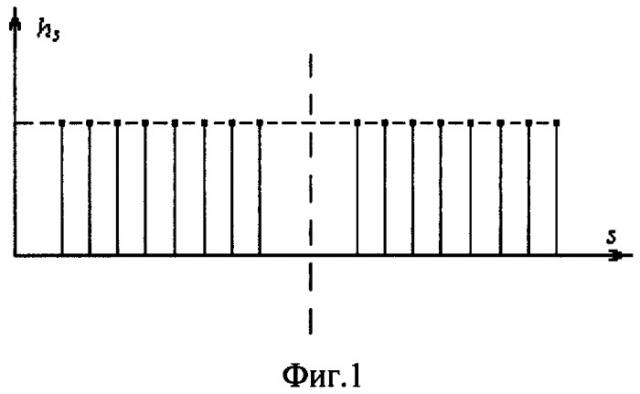
2. В то же время для модельной гистограммы вида, показанного на Фиг.1, критерий κ без введения порога (N=1) и с введением одного порога (N=2), дающего искомое разделение, равен нулю. Т.е. рассмотренный критерий не всегда позволяет сравнивать разбиения с одинаковым числом порогов.

Задачей изобретения является создание способа автоматизированного разбиения на группы уровней яркости пикселов растровых изображений по значениям их повторяемости, который не будет иметь перечисленных выше недостатков.

Поставленная задача достигается тем, что предложен способ автоматизированного разбиения на группы уровней яркости пикселов растровых изображений по значениям их повторяемости, заключающийся в том, что для заданного растрового изображения, у которого есть ряд уровней яркости пикселов, имеющих значения повторяемости и общий объем, вводится разбиение на группы подряд стоящих уровней яркости, причем вначале группы идет возрастание значений повторяемости, а в конце - их убывание, соотношение объема каждой группы к общему объему должно быть не менее 1/8 и число групп не должно быть больше 4, для каждой группы введен показатель качества, а для всего разбиения - обобщенный показатель качества, критерием оптимальности которого является минимум, согласно изобретению в качестве показателя качества группы принимается момент инерции значений повторяемости относительно медианы группы, для которой суммы повторяемостей слева и справа равны между собой, а обобщенный показатель качества всего разбиения на группы имеет вид:

где N - число групп,

- объем группы с номером u (u=1, ..., N),

{h₁, ..., h_n} - повторяемости, соответствующие уровням яркости пикселов {s₁, ..., s_n},

- показатель качества группы с номером u,

s^u _н, s^u _к - начальное и конечное значения яркости в группе с номером u,

s^u _м - медиана значений яркости в группе с номером u.

Рассмотрим для n уровней яркости пикселов s_i(i=1,...,n) гистограмму их повторяемости Н={h₁,...,h_n}. Как показали эксперименты, для фиксированной группы s^u частным критерием качества, наилучшим образом отражающим свойство "кучности", является не дисперсия, а момент инерции группы относительно ее медианы s^u _м:

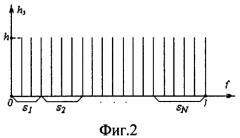
Для того чтобы объединить выбранные частные критерии в один общий, рассмотрим в качестве модельного равномерное распределение характеристики интенсивности h с большим числом значений, равномерно распределенным в интервале [0,1] (Фиг.2). В данной гистограмме критерий не должен выделять пороги, поскольку на самом деле их не существует.

При отсутствии деления гистограммы на группы общий момент инерции относительно медианы равен

где Q=h·1 - общий объем гистограммы.

При произвольном разбиении данной гистограммы на N групп, которые по оси s занимают отрезки длиной s₁, s₂,...,s_N(s₁+s₂+...+s_N=1), их моменты инерции будут равны

Значение общего суммарного критерия останется неизменным (до и после разбиения) в том случае, когда каждый частный критерий f(g^u) будет включен в общую сумму с весовым коэффициентом 1/(s_u ²).

Вводя в рассматриваемых задачах в коэффициенты вместо s_u величины объемов групп q^u, получим обобщенный критерий следующего вида:

Данный критерий позволяет эффективно выделять как оптимальное число N групп в гистограмме, так и состав групп в тех случаях, когда характер гистограммы позволяет сделать это.

Для практической реализации предложенного способа может быть использован следующий алгоритм.

ИСХОДНЫЕ ДАННЫЕ.

Для некоторой числовой характеристики s задана гистограмма H, а также пороговое значение δ предельно малого относительного объема групп. Необходимо выяснить возможность порогового разделения гистограммы для заданной гистограммы. Если возможно, то найти такое число N групп в гистограмме и их состав, при котором достигает минимума обобщенный критерий при условии, что относительный объем групп не превышает δ и разделение групп производится в области локальных минимумов на гистограмме.

ПРЕДВАРИТЕЛЬНЫЕ ДЕЙСТВИЯ.

Вычисляется общий объем гистограммы Q и пороговое предельно малое значение объема группы Q_пр=δ·Q.

Поскольку разделение должно происходить в области локальных минимумов на гистограмме, то работа алгоритма начинается с их поиска.

ШАГ 1. Предварительный просмотр гистограммы. Выделение всех локальных минимумов на ней. Данные минимумы бывают одиночные (когда в точке минимума s=s_i выполняется условие h_S(i-1)>h_{S i}<h_S(i+1)) и групповые, когда минимальное значение принимают несколько подряд стоящих значений гистрограммы. В обоих случаях возникает необходимость задания порогового значения относительно минимальных значений. Поскольку значение критерия меньше, когда состав групп более однороден по величине значений h_S, то минимумы присоединяем к тем промежуточным группам значений, у которых более близкое среднее значение. В итоге создается линейный массив возможных порогов Р некоторой длины n_m. Если локальных минимумов на гистограмме нет, то она считается неразделимой на группы. Выход из алгоритма с отрицательным ответом.

ШАГ 2. Расчет начального значения критерия при отсутствии порогов: F_нач=F(N=1). Это же значение присваиваем текущему минимальному значению критерия: F_min=F_нач.

ШАГ 3. Перебор всех возможных вариантов порогов, вычисление значений критерия для них и выбор оптимального варианта.

3.1. Генерация возможных порогов. Поскольку для каждого возможного порога Р_i есть две возможности - входить в набор или нет, то общее число нерассмотренных вариантов порогов равно (один вариант, в котором в набор не вошел ни один порог, рассмотрен на ШАГЕ 2). Кодируя каждый из вариантов числом от 1 до , вхождение каждого из порогов в выбранном варианте i находим, разлагая это число в двоичной системе в вектор длины n_m. Те позиции j, на которых стоит 1, задают вхождение j-го порога в набор. Если стоит 0, то порог не входит в набор.

3.2. Проверка набора порогов по предельно малому объему группы Q_пр. Каждый конкретный набор порогов задает на гистограмме некоторый набор групп. Объемы всех групп Q^u проверяются на выполнение условия Q^u>Q_пр. Если хотя бы для одной из групп условие не выполнено, весь набор исключается из дальнейшего анализа.

3.3. Вычисление критерия. Проверка оптимальности пороговых порогов. Для выбранного набора групп s¹, s²,...,s^N вычисляется значение критерия F(s¹, s²,...,s^N). Если выполняется условие F(s¹, s²,...,s^N)<F_min, то найдено более оптимальное разбиение на группы. В этом случае выполняем присваивание F_min=F(s¹, s²,...,s^N) и запоминаем соответствующее пороговое разделение.

ШАГ 4. Итоговая проверка. Если после окончания перебора всех вариантов порогов выяснилось, что F_min=F_нач, то это свидетельствует, что гистограмма плохо разделима на группы и введение порогов на ней нецелесообразно. Выход из алгоритма с отрицательным ответом.

Если F_min<F_нач, то получено искомое оптимальное число групп N и разбиение множества значений на группы {s}.

Пример.

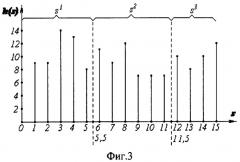
ИСХОДНЫЕ ДАННЫЕ. Для двухцветного растрового 16-цветного изображения (n=16) размером 20×80 получена гистограмма, показанная на Фиг.3, у которой

h₀=14; h₁=9; h₂=9; h₃=14; h₄=13; h₅=8; h₆=11; h₇=9; h₈=12; h₉=7; h₁₀=7; h₁₁=7; h₁₂=10; h₁₃=8; h₁₄=10; h₁₅=12.

Пороговое значение предельно малого относительного объема групп δ=0,15.

Необходимо выяснить возможность порогового разделения гистограммы для заданной гистограммы. Если возможно, то найти такое число N групп в гистограмме и их состав, при котором достигает минимума обобщенный критерий при условии, что относительный объем групп не превышает δ и разделение групп производится в области локальных минимумов на гистограмме.

ПРЕДВАРИТЕЛЬНЫЕ ДЕЙСТВИЯ.

Вычисляется: 1) общий объем гистограммы: Q=160, 2) пороговое предельно малое значение объема группы Q_пр=δ·Q=0,15·160=24.

ШАГ 1. Выделены внутренние локальные минимумы гистограммы, которые задают начало возможных групп: 1, 6, 9, 13. Общее число их равно 4.

ШАГ 2. Начальное значение критерия при отсутствии порогов: F_нач=F(N=1)=0,141392. Это же значение присваиваем текущему минимальному значению критерия: F_min=F_нач.

ШАГ 3. Перебор всех возможных вариантов порогов, вычисление значений критерия для них и выбор оптимального варианта.

Вариант 1000, значение критерия: F=0,146384>F_min.

Вариант 0100, значение критерия: F=0,144421>F_min.

Вариант 1100, значение критерия: F=0,14888>F_min.

Вариант 0010, значение критерия: F=0,131995<F_min, F_min=0,131995.

Вариант 1010, значение критерия: F=0,134505>F_min.

Вариант 0110, значение критерия: F=0,128107<F_min, F_min=0,128107.

Вариант 0001, значение критерия: F=0,133057>F_min.

Вариант 1001, значение критерия: F=0,132206>F_min.

Вариант 0101, значение критерия: F=0,140083>F_min.

Вариант 1101, значение критерия: F=0,144533>F_min.

У вариантов 0011, 1011, 0111, 1111 есть группы с объемом, меньшим Q_пр, поэтому они не анализируются.

В итоге оптимальным принят вариант 0110 со значением критерия F=0,128107. Пороговые значения 5,5 и 11,5. При этом N=3, s¹={0,1,2,3,4,5}, s²={6,7,8,9,10,11}, s³={12,13,14,15}.

Способ автоматизированного разбиения на группы уровней яркости пикселов растровых изображений по значениям их повторяемости, заключающийся в том, что для заданного растрового изображения, у которого есть ряд уровней яркости пикселов, имеющих значения повторяемости и общий объем, вводится разбиение на группы подряд стоящих уровней яркости, причем вначале группы идет возрастание значений повторяемости, а в конце - их убывание, соотношение объема каждой группы к общему объему должно быть не менее 1/8 и число групп не должно быть больше 4, для каждой группы введен показатель качества, а для всего разбиения - обобщенный показатель качества, критерием оптимальности которого является минимум, отличающийся тем, что в качестве показателя качества группы принимается момент инерции значений повторяемости относительно медианы группы, для которой суммы повторяемостей слева и справа равны между собой, а обобщенный показатель качества всего разбиения на группы имеет вид:

где N - число групп уровней яркости пикселов,

s¹, s²,...,s^N, - группы уровней яркости пикселов,

- объем группы с номером u (u=1,...,N),

{h₁,...,h_n} - повторяемости, соответствующие уровням яркости пикселов {s₁,...,s_n},

- показатель качества группы с номером u,

s^u _н, s^u _к - начальное и конечное значения яркости в группе с номером u,

s^u _м - медиана значений яркости в группе с номером u.