Способ определения содержания массовых долей элементов в материалах и сплавах

Способ определения содержания массовых долей элементов в материалах и сплавах

Иллюстрации

Показать все

Реферат

Изобретение относится к атомному эмиссионному спектральному анализу материалов и сплавов, а именно к определению содержания массовых долей элементов в материалах и сплавах.

В классическом атомном эмиссионном анализе известен ряд способов определения содержания массовых долей элементов в материалах и сплавах.

Так, например, известен способ определения массовых долей при эмиссионном спектральном анализе материалов и изделий, имеющий в своей основе эмпирическую формулу Ломакина-Шейбе - представление зависимости интенсивности I излучения низкотемпературной плазмы (НТП) от величины массовых долей элементов Ci в исследуемом материале [1].

По данному способу расчет параметров массовых долей элементов Ci производится по градуировочным графикам I=f(lgCi) в небольших интервалах изменения Ci, причем границы данных интервалов определяются экспериментально соответствующим подбором стандартных образцов-эталонов (СО).

Недостатком данного способа является необходимость иметь большое количество стандартных образцов, что приводит к дополнительным затратам времени на их анализ и создает определенные трудности в экспресс анализах.

Известны технические решения, в которых с помощью одного комплекта СО анализируют около 50 марок алюминиевых сплавов на многоканальных атомно-эмиссионных спектрометрах. Разработан метод построения эмпирических градуировочных характеристик на больших диапазонах изменения содержания таких, элементов как медь, цинк, магний [2].

В связи с тем, что такое построение с помощью одной аналитической линии для некоторых элементов невозможно из-за реабсорбции и самопоглощения, то задача решена с помощью двух аналитических линий определяемого элемента. Нелинейность учтена с помощью полиномиальных моделей градуировочных характеристик (ГХ), коэффициенты которых рассчитывались по методу наименьших квадратов.

Для повышения точности определения примесей в алюминиевых сплавах по единому комплекту государственных СО (ГСО) введено "инструментальное" взвешивание, сущность которого сводится к набору таких ГХ, по которым при определении состава пробы обеспечивается максимальная вероятность получения фактически наблюдаемых содержаний элементов. "Инструментальное" взвешивание позволяет сократить число используемых комплектов СО, градуировочных графиков, постоянно находящихся в памяти ЭВМ, или специальных таблиц.

Описанный выше способ оптического спектрального анализа основан на косвенных измерениях химического состава, причем за меру процентного содержания определяемого элемента в пробе сплава принимается относительная интенсивность спектральной линии этого элемента при существовании фундаментальной связи между ними.

Связь устанавливается по данным градуировки спектрометра с помощью комплекта ГСО известного состава.

Однако реализация данного способа требует:

большого объема работ, связанных с занесением в память ЭВМ градуировочных характеристик;

наличия комплекта из нескольких СО;

при проведении анализа возбуждения спектра не только пробы, но и комплекта ГСО, а также измерения интенсивности спектральных линий пробы и ГСО.

Наиболее близким решением, взятым в качестве прототипа, является способ определения содержания массовых долей элементов в материалах и сплавах, в котором количество СО уменьшено до одного [3].

Известный способ включает возбуждение излучения образца, измерение почернения основной линии элемента и линии сравнения, расчет содержания испытуемого элемента в образце, регистрацию эмиссионного спектра СО для определения параметра М_э, характеризующего способность к излучению НТП пробы относительно СО по каждому элементу, и параметра (АХ)_эп, характеризующего устойчивое состояние НТП в СО по отношению к пробе, связанные соотношением

где М=(2/π)arctg{[S_i(S_i + S_icp - ΔS_э)/S_i(S_i + S_iср+ΔS_э)]C_iэ};

b_ээ=1-(1/π)arctg[(АХ)_ээC_iэ];

C_iэ, ΔS_э - содержание элемента и разность почернений основной линии и линии сравнения в СО;

S_i, S_icp - почернение основной линии и линии сравнения для пробы;

В, D - коэффициенты пропорциональности, определяемые по таблице соответствия по величине М, и рассчитывают ориентировочное содержание искомого элемента в пробе С_х по системе уравнений:

S₀=250 - максимальное почернение, определяемое микрофотометром (паспортное значение).

Анализ известных способов определения содержания массовых долей элементов в материалах и сплавах показывает, что использование существующей в настоящее время полуэмпирической теории расчета количественного содержания элементов не предусматривает совокупность существующих объемных взаимодействий частиц в облаке НТП, сопровождающихся энергетическими превращениями атомов и ионов. Именно поэтому диапазон достоверного анализа по методу контрольного СО ограничен, что в значительной мере снижает точность и достоверность анализа при использовании отраслевых СО и СО предприятий.

Ограниченность их применения обуславливается также внутренними энергетическими превращениями при изменении количественных соотношений компонентов проб. Все это приводит к тому, что даже на ограниченном интервале изменения концентрации могут возникать погрешности при определении С_х.

Задачей данного изобретения является дальнейшее повышение точности и достоверности определения количественного содержания элементов в материалах и сплавах.

Поставленная задача достигается тем, что вводятся в рассмотрение изолированные системы расчета и метод последовательных приближений, учитывающие различный матричный состав и возможные различия в условиях проведения эксперимента для эталона и пробы. Для расчета в широком диапазоне изменения концентраций анализируемых элементов используется один контрольный эталон.

Для определения содержания массовых долей элементов в материалах и сплавах используется способ, включающий возбуждение излучения образца в низкотемпературной плазме, регистрацию эмиссионного спектра образца, измерение интенсивности аналитической линии элемента и линии сравнения, расчет содержания искомого элемента в пробе, по физической модели, содержащей выражения параметра (αχ)_эх, характеризующего устойчивое состояние низкотемпературной плазмы в стандартном образце по отношению к пробе, и параметра М_iэ, характеризующего способность к излучению низкотемпературной плазмы относительно стандартного образца по каждому элементу, определяемые соотношениями

где

;

С_эi, ΔР_эi - содержание элемента и разность интенсивностей

анализируемой линии и линии сравнения элемента i в стандартном образце;

P_xi, P_xicp - интенсивности анализируемой линии и линии сравнения элемента i в пробе;

В, D - коэффициенты пропорциональности, определяемые параметром М_эi, рассчитывают энергетические параметры излучения пробы относительно эталона L′_хэ и L′_эх

производят корректировку и расчет новых значений интенсивностей спектральных линий в пробе Р_х и Р_хср так, что

где ΔР_х, ΣP_x, - разность и сумма интенсивностей анализируемой линии и линии сравнения элемента в пробе;

P′_x, P′_xcp, Р_х, Р_хср - измеренные и скорректированные параметры пробы;

L_хэ=L′_хэ+ΔL′;

ΔL′=1-(L′_хэ+L′_эх);

рассчитывают содержание искомого элемента в пробе С_х по системе уравнений

где

причем на промежуточных этапах в качестве эталона принимается расчетное значение концентрации С_ст=С_х, определяют расчетное значение интенсивности излучения спектральной линии для эталона по выражению

где v=(f+fd²+1+d²)/[2d(f-1)];

d=tg[(π/2)·(P_э+P_эср)/2P₀];

h=[tg(π/2)·(P_э/P₀)]/[tg(π/2)·(P_эср/P₀)];

f=U_эхh=(1/U_хэ)h,

а расчет концентрации и корректировку параметров излучения производят до тех пор, пока не выполнится заданная точность вычислений

где Δ_Рст - расчетное значение параметра излучения во внутреннем стандарте;

Δ_Рх - измеренное значение параметра излучения в пробе;

- относительная погрешность вычислений.

По предлагаемому способу выполняется расчет ряда виртуальных эталонов с контролем по интенсивности излучения, содержание в которых последовательно приближается к искомой величине.

Способ является составной частью автоматизированной системы определения количественного состава элементов в материалах и сплавах с фотоэлектрической регистрацией спектров. В качестве приемников излучения используются твердотельные многоканальные линейные приборы с зарядовой связью, преобразующие интенсивности излучения непрерывного спектра в дискретный сигнал, после обработки которого получают параметры анализируемых спектральных линий. В качестве параметров, участвующих в дальнейшем расчете количественного содержания, выбираются значения максимумов интенсивностей или площади, ограниченные контурами спектральных линий. Независимо от способа регистрации можно принять в качестве измеряемого параметра отображение интенсивности Р.

Исходными данными для расчета являются измеряемые параметры интенсивности излучения спектральных линий исследуемого элемента Р_х, Р_э и линий сравнения Р_хср, Р_эср для эталона и исследуемой пробы, а также концентрация С_э элемента в эталоне. Для неизолированной системы параметры пробы обозначены P′_x; P′_xcp:

где ΣР_э = Р_э + Р_эср; ΣP_x = P_x + P_xcp;

ΔР_э = Р_э - Р_эср; ΔР_х = Р_х - Р_хср.

Исходные данные системы (1) переводятся в изолированное состояние, отстраиваясь от различий матричного состава и возможных различий в условиях проведения эксперимента для эталона и исследуемой пробы.

Для этого рассчитываются относительные энергетические параметры излучения пробы относительно эталона L_хэ, L_эх

и параметры усиления спектрального излучения элемента пробы относительно эталона U_хэ, U_эх

где P₀ - максимальное значение измеряемого параметра (при фотоэлектрическом анализе V₀=10B).

Условием совместимых изолированных систем являются уравнения

Если при этом в системе эталон-проба не происходит поглощение излучения, то эта сумма равна 1. Если же часть энергии поглощается (ΣL′<1) или происходит излучение части энергии в окружающую среду (ΣL′>1), то для приведения системы в изолированное состояние следует учесть эту разницу внесением поправки

В соответствии с полученным L_хэ производится корректировка и получение новых значений Р_х и Р_хср, при этом следует учитывать, что параметры ΔP_x=const и ΔР_э=const, так как они являются мерой количественного содержания элемента в пробе и эталоне:

tg(π/2)L_хэ=(ΔР_х + Р_хср)/Р_хср(ΣP′_х - ΔР_э)/(ΣР′_x + ΔР_э)

после преобразований:

Р_хср=(ΔP_xΣP′_x - ΔР_хΔР_э)/[tg(π/2)L_хэ(ΣР′_х + ΔР_э) + ΔР_э - ΣР_х];

и расчетная формула преобразуется к виду:

tg(π/2)L_хэ=[(ΔP_x + P_xcp)/P_xcp][(ΔР_х + 2Р_хср - ΔР_э)/(ΔР_х + 2Р_хср + ΔР_э)].

После замены искомой величины Р_хср, решается приведенное квадратное уравнение следующего вида:

Решением этого уравнения является параметр линии сравнения элемента пробы Р_хср и затем из условия Р_х = ΔР_х + Р_хср определяется интенсивность элемента пробы.

В результате преобразований возникает исходная для вычислений равновесная система с параметрами:

В последующих преобразованиях будем находить параметры внутреннего стандарта и сравнивать полученные значения с исходными измеренными параметрами пробы в изолированной системе (2).

Необходимое условие взаимосвязи внутреннего стандарта и пробы выразим равенством параметров ΣР_э =ΣР_х = const.

Эта равновесная система для искомых Р_х и Р_хср будет симметричной относительно данных ΣР_э/2 и ΔР_х/2, т.е.

Для нахождения промежуточного значения концентрации элемента пробы С′_х=С_ст1 на первом этапе расчетов решается тождество относительно C_ст1 [1]:

где

- параметр излучения контрольного эталона;

- задающий энергетический параметр элемента пробы С_х, или эталона С_э соответственно (восприимчивость к спектральному излучению);

- коэффициент самопоглощения атомов и ионов в низкотемпературной плазме;

Далее, на основе уравнений (2) для L_эх, рассчитывается разность ΔР_ст1 элемента пробы, соответствующая найденному по п.5 значению C_ст1:

где

Фиксируются данные контрольного эталона и пробы на начало второго этапа вычислений:

Пункты 4-7 повторяются на втором этапе расчетов. В конце этих вычислений определяются исходные данные равновесной системы аналогичные (18).

Этапы повторяются до тех пор, пока с заданной степенью точности полученное значение разности входных параметров внутреннего стандарта ΔP_стi на последнем этапе вычислений i не будет совпадать с измеренным значением в пробе ΔР_х, т.е.:

для заданного уровня относительной погрешности δ_Р.

Экспериментальные данные определения процентного содержания Si, Си, Mg и Mn в сплаве литейного алюминия АК5М, полученные на модернизированной фотоэлектрической установке МФС-8М, приведены в таблице. В качестве приемников спектрального излучения использованы блоки регистрации типа SKCCD на основе диодных линеек. В качестве контрольного эталона С_кэ и исследуемой пробы использованы стандартные образцы из комплекта ГСО №11. Значение исследуемой пробы сравнивалось с заранее известным содержанием С_гсо.

Таблица
Опытные данные способа последовательных приближений
Элемент	Cкэ	Сгсо	Данные Сxi по этапам	δC, %
C1	C2	С3	C4=Сх
Si	4.09	5.29	5.124	-	-	5.331	0.78
6.28	5.660	6.065	-	6.160	1.91
7.31	6.032	6.950	7.541	7.506	2.68
Cu	0.98	2.06	1.784	2.222	2.187	2.170	5.33
2.84	2.378	2.755	2.821	2.726	4.01
6.75	5.630	6.344	6.952	6.935	2.70
Mg	0.188	0.308	0.2757	0.321	-	0.315	2.27
0.482	0.394	0.467	-	0.501	3.94
0.497	0.406	0.486	-	0.506	1.81
Mn	0.156	0.219	0.203	-	-	0.226	3.20
0.402	0.355	0.414	-	0.391	2.74
0.740	0.580	0.663	0.800	0.768	3.81

Пример расчетов для фотоэлектрического анализа.

Ниже приведены промежуточные результаты расчетов для Мп в сплаве Ак5М по данным таблицы.

Исходные данные измеренных напряжений, пропорциональные интенсивностям спектральных линий (V_o=10B).

Находим L_хэ, для этого вычисляем L′_хэ, L_эх и ΔL:

L′_хэ=0.7137; L_эх=0.1397; ΔL=0.1466; тогда L_хэ=0.8603.

Определяем параметр V_xcp из выражения (17) и затем V_x для равновесной изолированной системы, для которой из соображений симметрии выполняется условие (19). Тогда получим V_xcp=1.5450; V_x=0.4300.

Таким образом, исходная равновесная система на начальном этапе вычислений имеет следующий вид:

Первый этап. Находим содержание C_x1, из решения тождества (10) с использованием (11)-(13), (2), (3):

C_x1=0.58; a_x=0.5501; b_x=0.9016; Q_x=0.4142; a_ст1=1.6360; b_ст1=0.9204;

Q_ст1=0.1160; К_ст1=1.3443; К_х=1.4002; U_хэ=3.573; Q_ст1U_хэ=0.4586.

Тогда C_x1=C₁=0.58 - внутренний стандарт первого этапа.

Определяем параметры V_x и V_xcp. Для этого в соответствии с уравнениями (15)-(18) находим значения d, h, К, f и v, а затем параметр ΔV_x=ΔV_ст1 из формулы (14) при C₁=0.58. Тогда получим:

К(С_х, С_э)=1.333; a_ст1=1.6360; b_ст1=0.9204; K_ст1=1.3443; Q_ст1=0.1160; Q_x=0.4140;

d=0.1563; h=0.0765; f=4.8825; v=5.0484.

Тогда ΔV_x=ΔV₁=-1.2700, или из соображений симметрии для равновесных систем имеем:

V₁=0.9875+(ΔV₁/2)=0.9875+0.6350=0.3525;

V_1cp=0.9875-(ΔV₁/2)=0.9875-0.6350=1.6225.

Второй этап. Исходная система:

Находим С_х2:

С_х2=0.663; а_х=0.4444; b_x=0.8975; Q_x=0.5321; а_чт2=0.5501; b_ст2=0.9016;

Q_ст2=0.4142; к_ст2=1.4002; к_х=1.4096; U_хэ=1.2843; Q_ст2U_хэ=0.532.

Тогда C_x2=C₂=0.663 - внутренний стандарт второго этапа.

Определим параметры V_x и V_xcp при С₃=0.75 по аналогии с предыдущим:

К(С_х, С_ст2)-1.0660; Q_x=0.5321; Q_х=0.4142;

d=0.1563; h=0.2128; f=3.9; v=5.5372.

Тогда ΔV_х=ΔV₃=-1.1566, и из условия симметрии для равновесных систем имеем:

V₂=0.9875+(ΔV₂/2)=9875+0.5783=0.4092;

V_2cp=0.9875-(ΔV₂/2)=0.9875-0.5783=1.5658.

Третий этап. Исходная система:

Находим С_х3.

С_х3=0.8; а_х=0.4212; b_x=0.8965; Q_x=0.5667; а_ст3=0.4444; b_ст3=0.8975;

Q_ст3=0.5321; к_ст3=1.4002; к_х=1.4118; U_x3=1.066; Q_ст3U_хэ=0.5671.

Тогда C_x3=C₃=0.80 - внутренний стандарт третьего этапа.

Определим параметры V_x и V_xcp при С₃=0.8. По аналогии с предыдущим:

К(С_х, С_ст3)=1.0660; Q_x=0.5667; Q_ст3=0.5321;

d=0.1563; h=0.2564; f=3.7215; v=5.5915.

Тогда ΔV_x=ΔV₃=-1.082, и из условия симметрии для равновесных систем имеем:

V₃=0.9875+(ΔV₃/2)=0.9875+0.5410=0.4465;

V_3ср=0.9875-(ΔV₃/2)=0.9875-0.5410=1.5285.

Четвертый этап. Исходная система:

Находим С_х4:

С_х3=0.77; а_х=0.4348; b_x=0.8971; Q_x=0.5459; a_ст4=0.4212; b_ст4=0.8965;

Q_ст4=0.5667; к_ст4=1.4118; к_х=1.4105; U_xст4=0.9524; Q_ст4U_xэ=0.5397.

Тогда C_x4=C_x=0.768 - внутренний стандарт четвертого этапа.

Определим параметры V_x и V_xcp при C₄=0.768. По аналогии:

ΔV_x=(4V_o/π)·arctg[-v±[(v²-1)^0.5]];

K(C_x, C_ст4)=1.01; Q_x=0.5459; О_ст4=0.5665;

d=0.1563; h=0.2869; f=3.6532;

v=5.7474. Тогда ΔV_x=ΔV₄=-1.114;

и из условия симметрии для равновесных систем имеем:

V₄=0.9875+(ΔV₁/2)=0.9875+0.5570=0.4305;

V_4cp=0.9875-(ΔV₁/2)=0.9875-0.5570=1.5455.

Таким образом, на четвертом, заключительном этапе параметры исследуемой аналитической пары имеют следующие численные значения:

Таким образом, относительная погрешность при определении разности напряжений в эталоне по сравнению с разностью напряжений элемента в пробе на четвертом этапе вычислений составила

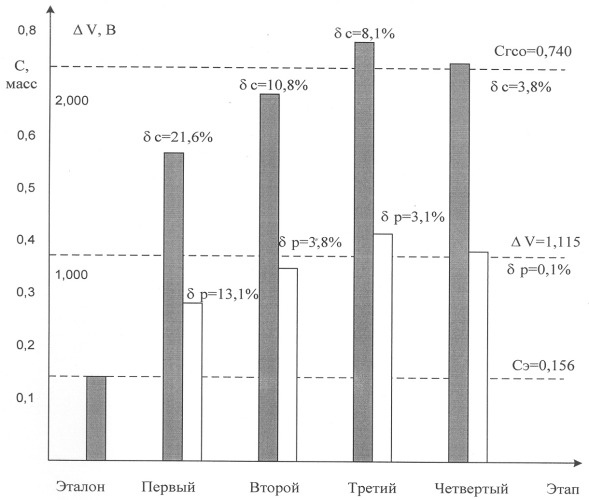
δ_р=(ΔV_x-ΔV_ст4)/ΔV_ср=(1.115-1.114)/1.1145=0.1%.

Погрешность в определении С_х = С_ГСО =0.740 составила

δ_С=(С_х - С_ГСО)/С_ГСО=(0.768-0.74)/0.74=3.8% на уровне С_э=0.156.

Погрешность аналитических вычислений можно определить из совместного решения уравнений (3), (4), (6) и (7).

Диаграммы изменения процентного содержания элементов и напряжений на выходе диодных линеек изображены на чертеже. Там же указаны получаемые относительные погрешности.

Полученные экспериментальные данные и проведенные вычисления позволяют говорить о более широком диапазоне использования одного контрольного эталона. Как показывают экспериментальные исследования различных марок материалов, содержание элементов в пробах относительно контрольных эталонов может отличаться в 10 и более раз. При этом погрешность конечного результата практически не изменяется и может колебаться в пределах от десятых долей процентов до (5-7)%.

При традиционных методах определения содержания с помощью градуировочных графиков при отношении 10>(С_х/С_э)>5 относительная погрешность может изменяться в пределах от 5 до 25%. При меньших диапазонах изменения концентраций ошибка измерений уменьшается. Предельным случаем расчетов при традиционных методах обработки результатов измерений является отличие в содержаниях элементов в образцах и пробах не более чем в 10 раз.

Технико-экономическая эффективность предлагаемого способа определения содержания массовых долей элементов в материалах и сплавах заключается в повышении точности и достоверности определения количественного содержания элементов в материалах и сплавах. В результате повышается экономичность, экспрессность и качество проводимых анализов за счет сокращения расходов на приобретение дорогостоящих комплектов ГСО и их использования в текущих анализах, сокращения времени на проведение анализов. Способ обеспечивает необходимые точность и достоверность получаемых результатов в соответствии с требованиями ГОСТ.

Литература

1. Нагибина И.М., Михайловский Ю.К. Фотографические и фотоэлектрические спектральные приборы и техника эмиссионной спектроскопии. - Л.; Машиностроение, 1981. - С.92-103.

2. Морозов Н.А. Методы оптического спектрального анализа алюминиевых сплавов с применением ЭВМ. - Заводская лаборатория, 1986, №9. - С.21-28.

3. Пат.2035718 Россия, МКИ G01N 21/67. Способ определения массовых долей элементов в материалах и сплавах. // Никитенко Б.Ф., Одинец А.И., Казаков Н.С., Кузнецов В.П., Кузнецов А.А. 1995. Бюллетень №14. - Прототип.

Способ определения содержания массовых долей элементов в материалах и сплавах, включающий возбуждение излучения образца в низкотемпературной плазме, регистрацию эмиссионного спектра образца, измерение интенсивности аналитической линии элемента и линии сравнения, расчет содержания искомого элемента в пробе, отличающийся тем, что контролируют интенсивность излучения аналитической линии элемента в эталоне при последовательном приближении содержания элемента к искомой величине и производят корректировку параметров излучения пробы для измерения аналитической линии элемента, при этом используют физическую модель, содержащую выражения параметра (αχ)_эх, характеризующего устойчивое состояние низкотемпературной плазмы в стандартном образце по отношению к пробе и параметра М_iэ, характеризующего способность к излучению низкотемпературной плазмы относительно стандартного образца по каждому элементу, определяемые соотношениями

где

С_эi ΔР_эi - содержание элемента и разность интенсивностей анализируемой линии и линии сравнения элемента i в стандартном образце;

P_xi, P_xicp - интенсивности анализируемой линии и линии сравнения элемента i в пробе;

В, D - коэффициенты пропорциональности, определяемые параметром М_эi, рассчитывают энергетические параметры излучения пробы относительно эталона L′_хэ и L′_эх

производят корректировку и расчет новых значений интенсивностей спектральных линий в пробе Р_х и Р_хср так, что

где ΔР_х, ΣР_х, - разность и сумма интенсивностей анализируемой линии и линии сравнения элемента в пробе;

P′_x, P′_xcp, Р_х, Р_хср - измеренные и скорректированные параметры пробы;

L_хэ=L′_хэ+ΔL′;

ΔL′=1-(L′_хэ+L′_эх);

рассчитывают содержание искомого элемента в пробе С_х по системе уравнений

где

причем на промежуточных этапах в качестве эталона принимается расчетное значение концентрации С_ст=С_х, определяют расчетное значение интенсивности излучения спектральной линии для эталона по выражению

где v=(f+fd²+1+d²)/[2d(f-1)];

d=tg[(π/2)·(P_э+P_эср)/2P₀];

h=[tg(π/2)·(P_э/P₀)]/[tg(π/2)-(P_эср/P₀)];

f=U_эхh=(1/U_эх)h,

а расчет концентрации и корректировку параметров излучения производят до тех пор, пока не выполнится заданная точность вычислений

где Δ_Рст - расчетное значение параметра излучения во внутреннем стандарте;

Δ_Рх - измеренное значение параметра излучения в пробе;

- относительная погрешность вычислений.