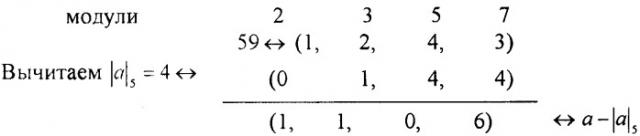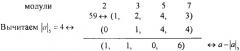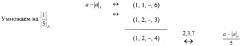Нейронная сеть для деления чисел, представленных в системе остаточных классов

Нейронная сеть для деления чисел, представленных в системе остаточных классов

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительным модулярным нейрокомпьютерным системам и предназначено для выполнения операции деления над числами, представленными в системе остаточных классов (СОК).

Известно устройство для деления чисел в системе остаточных классов (Овчаренко Л.А., Лопатин Д.С. Деление числа в модулярном коде на основание системы счисления // Телекоммуникации. - 2002. - №6. - С.7-10), содержащее табличные вычислители, когерентный преобразователь модулярного кода, устройство отображения и сумматор по модулю.

Недостатком данного устройства является большой объем оборудования и низкая скорость деления чисел.

Наиболее близким к данному изобретению техническим решением является устройство, представленное в виде "Нейронной сети для округления и масштабирования чисел, представленных и системе остаточных классов" (Патент RU №2271570, G06F 3/04, опубликован 10.03.2006, бюл. №7), содержащее входной слой нейронов, нейронную сеть конечного кольца (НСКК) определения ранга числа, нейронную сеть конечного кольца вычисления остатка по основанию n+1, n нейронных сетей конечного кольца вычисления масштабированного числа.

Недостатком устройства является большой объем оборудования и низкая скорость округления.

Однако такие нейронные сети предназначены для округления и масштабирования чисел, представленных в системе остаточных классов.

Целью данного изобретения является расширение возможностей известной нейронной сети для выполнения операции деления чисел, повышения скорости деления и уменьшения объема оборудования.

Поставленная цель достигается тем, что в нейронную сеть введена нейронная сеть для расширения кортежа числовой системы вычетов. Таким образом, нейронная сеть для деления чисел, представленных в системе остаточных классов будет состоять из входного слоя 2 с нейронами 7, (n-1) нейронных сетей конечного кольца (НСКК) для суммирования 3 с весовыми коэффициентами w 8, (n-1) НСКК для умножения 4 с весовыми коэффициентами w_i 7, равными , нейронной сети для расширения кортежа числовой системы вычетов 5 (описание изобретения к патенту RU 2256226⁽¹³⁾ С2, G06N 3/04, опубликовано 10.03.2005, бюл. 19), входа 1 и выхода 6.

В связи с тем, что модулярная арифметика целочисленная, то при вычислениях промежуточные значения операндов могут переполнять динамический диапазон. Подобная проблема может возникнуть и в традиционных компьютерах, если они оперируют с целыми числами. Во избежание переполнения надо промасштабировать (уменьшить) значения операндов. Промасштабированные величины затем используются в следующих итерациях. Это означает, что операция масштабирования должна применяться к данным с использованием заранее заданной константы, которая округляется до ближайшего целого. Все эти операции связаны с операцией деления.

Деление в модулярной арифметике относится к немодульным операциям и является одной из важнейших операций в модулярной компьютерной арифметике, так как лежит в основе многих других операций и входит в состав операций вычислительных алгоритмов.

Операцию деления в СОК можно отнести к одной из трех различных форм:

1. Деление с нулевым остатком.

2. Округление и масштабирование.

3. Основное деление.

Рассмотрим все основные формы модулярного деления.

При делении с нулевым остатком известно, что делимое представляет собой целое число, кратное делителю, а также известно, что делитель и Р являются взаимно простыми. Эта категория имеет ограниченную область использования, поскольку должно быть известно априори, удовлетворены ли условия, необходимые для осуществления операции.

Если а делится на b без остатка, и наибольший общий делитель (НОД) величин а и b равен 1, то

для всех p_i, где - мультипликативная обратная к b величина, взятая по модулю p_i.

Если b не делит a, то величина не является целой и выражение не определено. Следовательно, (1) не имеет смысла.

Пример 1. Деление с нулевым остатком.

Для модулей p₁=29, p₂=32 и p₃=31 разделим число 1872 на 9.

Решение. Остаточное представление 1872 - это (16, 16, 12). Остаточное представление 9 это - (9, 9, 9), тогда для 1872/9=208 остаточный код

С другой стороны, если мы делим 1873 на 9 (1873 не делится на 9 без остатка), то получим

1873↔(17, 17, 13)·(13, 25, 7)=(18, 9, 29)↔6601, что абсолютно неправильно.

Рассмотрим теперь случай, когда при делении и масштабировании делимое является произвольным, а делителем может быть любой сомножитель Р, представляющий собой произведение первых степеней некоторых модулей. Это деление аналогично делению на степень числа 2 в двоичной арифметике в том смысле, что деление на числа, принадлежащие определенному ограниченному множеству, выполняется быстрее, чем деление на произвольный делитель. Деление в любой целочисленной системе счисления определяется формулой , где а представляет собой делимое, b - делитель, - целая часть отношения а к b (частное), а - остаток (наименьший целый положительный остаток). Целью алгоритма деления является нахождение для значении b из ограниченной области. Заметим, что . Следовательно, в системе вычетов представляется величинами , где принимают целые значения. Если b совпадает с одним из p_i или является произведением первых степеней некоторых модулей p_i, то можно найти. Тогда, согласно (1), используемой в форме деления с нулевым остатком, для всех i, для которых НОД величин p_i и b равен 1, можно получить

Это уравнение задает цифры системы вычетов для для всех таких цифр, что МОД величин p_i и b равен 1. Остальные цифры могут быть найдены с помощью метода расширения базы. Таким образом, алгоритм деления состоит из двух этапов:

1. Деление с нулевым остатком.

2. Расширение базы.

Процесс деления покажем числовым примером.

Пример 2. Деление положительного числа единичным модулем. Для модулей р₁=2, р₂=3, p₃=5 и р₄=7 определим остаточное представление значения целого числа . Пусть а имеет остаточный код (1, 2, 4, 3)↔59, В качестве делителя используется модуль p₃.

Решение. Сначала определим остаточное представление числа, которое делится на 5 и является ближайшим целым к а, не превышающим а, то есть . Это можно найти путем вычитания остатка а по модулю 5.

Результат делится на 5 кроме модуля p₃, который сам является делителем. Все модули простые по отношению к делителю. Применяем метод деления с нулевым остатком, при этом остаточную цифру по модулю 5 временно игнорируем.

Исходный интервал определения для всего набора модулей был равен [0-209], а оказался в интервале [0-41], поэтому остаточное представление (1, 2, -, 4) не ясно. Остаток по модулю 5 может быть найден путем расширения базы. Это можно сделать методом Гарнера (последовательный метод) или предлагаемому в данной работе (параллельным методом). Для этого остаток по модулю 5 примем за 0 в первом случае и за - во втором.

В методе Гарнера для замены вычитания сложением необходимо использовать дополнительный код, при этом для вычитания необходимо две операции Выигрыш предложенного метода оценивается как

Пример 3. Деление положительного числа несколькими модулями.

В примере 2 делителем был только один модуль. В примере 3 делителем является произведение двух модулей, а именно 3×5=15. Вначале делим на 3 и полученное частное является новым делимым для делителя, равного 5, деление на 5 выдает значения целого числа частного. Для завершения операции деления необходимо выполнить операцию расширения базы. Изменение последовательности деления сначала выполнить деление на 5, а затем на 3 не меняет результата.

Для модулей p₁=2, p₂=3, p₃=5 и р₄=7 число а=89↔(1, 2, 4, 5) разделим на число 15. Обозначим результат как z.

Для расширения базы внесем 0 в пропущенные колонки для метода Гарнера и обозначим как и - для предложенного метода.

Итак, для деления числа большим коэффициентом масштаба используется последовательное деление на простые числа и расширение базы модулей СОК.

Предложенный алгоритм деления состоит из совокупности модульных операций по модулю p_i и его можно легко реализовать нейронными сетями конечного кольца.

На чертеже представлена схема нейронной сети для деления чисел, представленных в СОК.

Принцип работы данного изобретения излагается ниже.

Нейронная сеть для деления чисел, представленных в системе остаточных классов, приведенная на чертеже, позволяет выполнить операцию деления исходного числа А=(α₁, α₂, ..., α_n) 1 на делитель, равный одному из модулей СОК p_j=b.

Остатки делимого числа А=(α₁, α₂, ..., а_n) 1 по системе модулей p₁, p₂, ..., p_n поступают на вход нейронов 7 входного слоя 2. С выходов нейронов входного слоя 2 значения остатков по модулям p₁, p₂, p_j-1p_j+1, ..., p_n поступают на входы (n-1) НСКК 3 с весовыми коэффициентами 8 w=1 для реализации вычислительной модели , где:

α_i - остатки числа А в СОК по p_i модулям; α_j - остатки делителя по модулю p_j для i=1, 2, ..., n, при этом i не включает j.

Выходные значения (n-1) НСКК суммирования 3 поступают на входы (n-1) НСКК умножения 4, где реализуется вычислительная модель (2), при этом весовые коэффициенты w_i 7 равны . На выходах НСКК 4, кроме модуля делителя p_j формируется результат частного без разряда делителя в виде [α'₁, α'₂, ..., α'_j-1, α'_j+1, ..., a'_n), которые являются выходами нейронной сети.

Неизвестная цифра α'_j по модулю делителя определяется путем расширения базы СОК по известным остаткам α'_i, которые поступают на вход нейронной сети для расширения кортежа числовой системы вычетов 5. Вычисленный остаток α'_j является разрядом частного по модулю p_j и поступает на выход сети 6, восстанавливая кортеж частного (α₁, α'₂, ..., α'_j, ..., α'_n).

Время деления числа определяется тремя циклами синхронизации.

Аналогичным образом реализуется нейронная сеть для деления положительных чисел несколькими модулями.

Нейронная сеть для деления чисел, представленных в системе остаточных классов, содержащая входной слой нейронов, на входы которых поступают остатки делимого числа A=(α₁, α₂, ..., α_n) по системе модулей p₁, p₂, ..., p_n, выходы которых соединены с входами (n-1) нейронных сетей конечного кольца для суммирования значений остатков по модулям p₁, p₂, ..., p_j-1, p_j+1, ..., p_n, выходы которых соединены с входами (n-1) нейронных сетей конечного кольца для умножения, на выходах которых формируется результат частного без разряда делителя α′_j в виде (α′₁, α′₂, ..., α′_j-1, α′_j+1, ..., α′_n), выходы которых соединены с входами нейронной сети для расширения кортежа числовой системы вычетов, которые суммируют выходной кортеж частного, для получения разряда делителя α′_j, при этом выходом нейронной сети для деления чисел, представленных в системе остаточных классов, являются выходы нейронной сети конечного кольца для умножения и выход нейронной сети для расширения кортежа числовой системы вычетов.