Способ виброакустической диагностики машин

Способ виброакустической диагностики машин

Иллюстрации

Показать все

Реферат

Изобретение относится к машиностроению и может быть использовано для виброакустической диагностики машин - центробежных, поршневых, плунжерных насосов, компрессоров, вентиляторов, турбин, электроприводов и др.

Известен способ диагностики электрических дефектов машин, включающий анализ амплитудного спектра вибрации и распознавание частотных компонент, связанных с определенными дефектами (Патент США 5,739,698, кл. 324/772; 324/545).

Способ основан на измерении сигнала вибрации корпуса машины, вычислении амплитудного спектра, определении уровня гармонических составляющих спектра, связанных с определенными дефектами, частоты которых заносятся в базу данных перед проведением измерений.

Однако известный способ не позволяет обнаруживать дефекты, в условиях изменения режима работы машины, износа деталей, т.к. в этом случае реальные частоты дефектов будут отличаться от расчетных значений. Кроме того, для работы известных систем требуется точное описание конструкции машины, причем ошибки, которые могут возникнуть при занесении этой информации в базу данных или отсутствие части информации о конструкции также приводят к снижению достоверности диагноза.

Известен также способ выделения информативных периодичностей процесса в электронасосной установке (Патент РФ 2254496, МПК F04D 13/10, 2004), в котором периодические и шумовые составляющие сигнала выделяют путем последовательного вычитания из предварительно сохраненного исходного сигнала сгенерированных периодических составляющих, параметры которых определяют по мгновенному спектру исходного сигнала.

Однако в известном способе поиск выделяемых периодических составляющих осуществляется по максимуму мощности первой гармоники, что в случае использования для виброакустических сигналов, где гармоника с максимальным уровнем может отличаться от первой, приводит к ошибке.

В качестве прототипа известен способ виброакустической диагностики машин периодического действия, включающий выделение периодических и случайных компонент вибрации машины, обусловленных ее работой, с дальнейшим построением виброакустического вектора, по направлению и величине которого судят о виде и степени дефекта (Патент РФ 1280961, МПК G01М 13/02, 1986).

В данном способе периодические компоненты последовательно выделяют линейкой синхронных гребенчатых фильтров из исходного сигнала, причем частоту настройки гребенчатых фильтров устанавливают пропорционально частоте первой гармоники периодической компоненты, имеющей максимальную мощность. В результате формируют диагностический вектор, по направлению и величине которого судят о виде и степени дефекта, причем в качестве составляющих вектора используют амплитуды периодических компонент и координаты центра тяжести амплитудно-частотного спектра шумовой компоненты.

Недостатком известного способа является то, что включение в состав диагностического вектора только амплитуд периодических компонент ограничивает глубину и достоверность диагностики машины. Например, уровень оборотной периодической компоненты спектра виброакустического сигнала машины определяется степенью развития таких дефектов роторной части, как дисбаланс и расцентровка. В то же время отклонение частоты оборотной периодической компоненты, определяемой ее первой гармоникой, от номинального расчетного значения несет в себе информацию о степени сопротивления вращению, трении, что может быть связано, например, с состоянием смазки.

Другим недостатком известного способа является его работа в условиях неограниченной длительности сигнала. Реальные измерения виброакустических сигналов ограничены во времени, причем длительность измеренного сигнала определяет точность оценки частоты гармонической составляющей сигнала по его спектру dF, которая определяется по выражению:

где Т - длительность измеренного сигнала.

Из выражения (1) следует, что для уменьшения погрешности оценки частоты гармоники необходимо увеличивать длительность сигнала. Но при использовании данного способа в многоточечных системах диагностики, с последовательным измерением точек, увеличение длительности измеряемых сигналов приведет к увеличению общего цикла измерений, что может повлечь за собой пропуск дефекта и также снижает достоверность диагноза.

Для уточнения оценки частоты при ограниченной выборке сигнала используют методы интерполяции значения неизвестной частоты, расположенной в пределах ширины полосы дискретного спектра, по значениям соседних боковых спектральных составляющих, определяемых видом используемого окна взвешивания. Например, известен способ диагностики (Патент США 6,484,112, МПК G01R 29/02), в котором уточненную оценку частоты сигнала находят путем расчета корректирующего коэффициента при использовании окна Хамминга. Однако в данном способе не учитывается информация о состоянии машины, заключенная в отклонении уточненного, фактического, значения частоты группы кратных гармоник от его номинального значения, определенного конструкцией машины.

Техническая задача, решаемая изобретением, - повышение достоверности диагностики при распознавании известных периодических компонент в условиях ограниченной длительности сигнала.

Технический результат достигается тем, что в заявленном способе диагностики для каждой выделяемой периодической компоненты определяют отклонение фактического значения частоты каждой периодической компоненты от расчетного значения и также включают его в состав диагностического вектора, причем фактическое значение частоты периодической компоненты определяют как среднее значение фактических частот входящих в нее гармоник, приведенных к первой гармонике, с поправкой на коэффициент коррекции, определяемый видом функции окна преобразования Фурье, причем отклонение, фактическую частоту и коэффициенты коррекции определяют по формулам:

Δ=F_ру-F_ро, (2)

F_iy=F_i0+K_i·dF,

где F_ру - фактическое значение частоты выделяемой периодической компоненты;

F_p0 - расчетное (паспортное) значение частоты выделяемой периодической компоненты;

F_iy - фактическое значение частоты i-й гармоники выделяемой периодической компоненты;

F_i0 - центральная частота полосы спектра, в которой находится фактическое значение частоты i-й гармоники выделяемой периодической компоненты;

dF - ширина единичной полосы спектра БПФ преобразования;

К_i - коэффициент коррекции i-й гармоники, определяемый видом функции окна взвешивания Ханна, используемого при преобразовании Фурье;

U_i0 - амплитуда максимальной составляющей спектра в окрестности i-й гармоники;

U_i1 - амплитуда соседней боковой составляющей, имеющей меньшую частоту (расположенную слева от максимальной);

U_i2 - амплитуда соседней боковой составляющей, имеющей большую частоту (расположенную справа от максимальной);

i - номер гармоники периодической компоненты.

Анализ отличительных признаков предлагаемого способа виброакустической диагностики машин показал, что:

- включение в состав диагностического вектора отклонений фактических значений частот выделяемых периодических компонент от их расчетных значений повышает достоверность диагностики путем привлечения для диагностики дополнительной информации о величине сопротивления вращению ротора машины и других вращающихся деталей, например, сепаратора и тел качения подшипников, скольжения ротора асинхронного электродвигателя и т.д.;

- вычисление отклонения фактических значений частот выделяемых периодических компонент от их расчетных значений по выражениям (2-4) позволяет увеличить точность этой оценки в условиях ограниченной длительности сигнала.

Сущность способа поясняется чертежами, где изображено на:

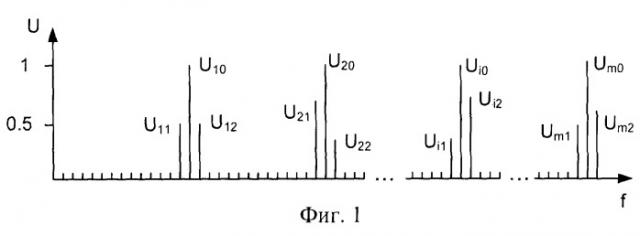
фиг.1 - амплитудный спектр сигнала, включающего периодическую компоненту;

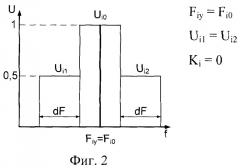
фиг.2 - распределение уровней боковых лепестков i-ой гармоники при совпадении фактической частоты гармоники с центральной частотой единичной полосы (F_iy=F_io);

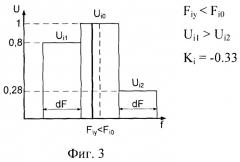
фиг.3 - распределение уровней боковых лепестков i-ой гармоники в случае, когда фактическая частота гармоники меньше центральной частоты единичной полосы (F_iy<F_io);

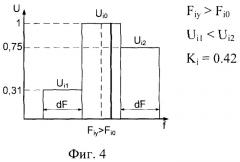
фиг.4 - распределение уровней боковых лепестков i-ой гармоники в случае, когда фактическая частота гармоники больше центральной частоты единичной полосы (F_iy>Р_io);

фиг.5 - амплитудный спектр сигнала виброскорости электродвигателя центробежного насосного агрегата с разрешением спектра dF=2,5 Гц;

фиг.6 - расчет уточненной (фактической) частоты периодической составляющей сигнала виброскорости электродвигателя центробежного насосного агрегата;

фиг.7 - амплитудный спектр сигнала виброскорости электродвигателя центробежного насосного агрегата с разрешением спектра dF=0,1 Гц и расчет фактической частоты периодической компоненты по частотам максимальных гармоник, без использования метода уточнения.

Реальный спектр сигнала, полученный путем применения быстрого преобразования Фурье (БПФ), имеет дискретный характер, причем ширина единичной полосы спектра (dF) определяется временем выборки сигнала по выражению (1). В окрестностях m гармоник периодической компоненты сигнала дискретный спектр будет иметь максимальные составляющие U_i0-U_m0 (фиг.1). Рядом с каждой максимальной составляющей спектра по обе стороны будут находиться две боковые составляющие (U_i1 - слева, U_i2 - справа), причина появления которых связана с влиянием утечки алгоритма БПФ - перетеканием части энергии сигнала через боковые лепестки единичной полосы спектра. Величина этой утечки определяется видом используемого окна взвешивания, используемого в преобразовании и величиной смещения реальной частоты гармоники F_iy относительно середины единичной полосы спектра, в которой она находится.

При совпадении фактической частоты i-й гармоники F_iy с центральной частотой единичной полосы F_io амплитуды боковых составляющих будут равны (U_i1=U_i2) (фиг.2). При отклонении фактической частоты гармоники от центральной частоты единичной полосы амплитуды боковых составляющих гармоник будут отличаться, причем при F_iy<F_i0 U_i1>U_i2 (фиг.3), при F_iy>F_i0 U_i1<U_i2 (фиг.4).

Значение уточненной (фактической) частоты i-й гармоники определяют по выражению:

где F_iy - уточненная частота i-ой гармоники;

F_i0 - центральная частота единичной полосы спектра, в которой находится частота i-й гармоники;

К_i - коэффициент уточнения частоты i-й гармоники, определяемый видом функции окна взвешивания;

dF - ширина полосы спектра.

В практике вибродиагностики наибольшее распространение получило окно взвешивания Ханна. По сравнению с другими окнами (Хэмминга, прямоугольное) оно имеет максимальную скорость спадания боковых лепестков (-18 Дб/октаву) при максимальном уровне бокового лепестка -31 Дб. Для окна Ханна коэффициент уточнения частоты определяют по выражению:

где U_i0 - амплитуда максимальной составляющей спектра в окрестности i-й гармоники;

U_i1 - амплитуда соседней боковой составляющей, имеющей меньшую частоту (расположенную слева от максимальной);

U_i2 - амплитуда соседней боковой составляющей, имеющей большую частоту (расположенную справа от максимальной).

После определения уточненной частоты каждой гармоники периодической составляющей, частоту первой гармоники можно определить как среднее значение частот всех гармоник, приведенных к первой:

где F_py - уточненная частота выделяемой периодической компоненты;

n - число гармоник периодической компоненты;

F_iy - уточненная частота i-й гармоники периодической компоненты;

i - порядковый номер гармоники.

Подставляя выражение (5) в (6), получим выражение для оценки фактической частоты периодической компоненты:

После определения фактической частоты периодической компоненты F_py вычисляют ее отклонение от расчетной частоты F_p, которую определяют по конструкции машины и номинальному режиму ее работы:

Δ=F_py-F_po.

Величину и знак (направление) отклонения Δ также используют в качестве информативного диагностического признака для оценки технического состояния машины.

Пример диагностики

Амплитудный спектр сигнала виброскорости электродвигателя центробежного насосного агрегата приведен на фиг.5. Длительность измеренного сигнала составляет Т=0,4 с. По выражению (1) определим частотное разрешение спектра, которое при данной длительности сигнала составляет dF=2,5 Гц.

Из чертежа видно, что амплитудный спектр сигнала содержит четыре гармоники, кратные частоте 50 Гц. Рядом с максимумами гармоник находятся боковые составляющие, амплитуды которых отличаются. На фиг.6 приведены значения амплитуд максимальных гармоник и их боковых составляющих, приведен также расчет уточненной (фактической) частоты периодической составляющей F_py=49,64 Гц, и ее отклонение от расчетной (паспортной) частоты F_po, которое для данного агрегата составляет 49,8 Гц. Полученное значение отклонения Δ=F_py-F_po=49,64-49,8=-0,16 Гц включается в состав диагностического вектора.

На фиг.7 приведен аналогичный спектр, рассчитанный по сигналу длительностью 10 с, при этом разрешение спектра составляет 0,1 Гц, Там же приведен расчет значений частоты периодической компоненты F_py=49,648 Гц и ее отклонения от расчетной частоты F_po=49,8 Гц без использования процедуры уточнения частоты, непосредственно по значениям единичных частот полос спектра, в которые попадают гармоники компоненты. Результат показывает, что значение отклонения Δ=0,152 Гц, полученное по спектру с высоким разрешением, отличаются от значения Δ=0,16 Гц, полученного с использованием данного метода не более чем на 5%, при этом длительность сигнала высокого разрешения в 25 раз больше длительности исходного.

В данном случае повышенное отклонение Δ=-0,16 Гц связано с увеличением скольжения ротора электродвигателя из-за замерзшей консистентной смазки подшипников, что часто является причиной выхода их из строя.

Таким образом, предлагаемый способ виброакустической диагностики машин обеспечивает повышение достоверности диагностики в условиях короткой выборки сигналов, что позволяет реализовать на его основе быстродействующие многоканальные системы диагностики и мониторинга технического состояния оборудования, существенно снижающие расходы предприятия на его ремонт и эксплуатацию, предотвращающие потери от внезапных аварий.

Способ виброакустической диагностики машин, включающий выделение n периодических и шумовую компоненту виброакустического сигнала, с дальнейшим построением диагностического вектора, по направлению и величине которого судят о виде и степени дефекта, причем шумовую компоненту выделяют путем последовательного подавления известных периодических компонент, отличающийся тем, что с целью повышения достоверности диагностики частоты известных выделяемых n периодических компонент, определяемых по частоте 1-й гармоники, входящей в каждую компоненту, устанавливают пропорционально частоте опорной периодической компоненты, которую находят путем поиска в заданном диапазоне частот, с коэффициентами пропорциональности, определяемыми конструкцией машины, определяют отклонение фактического значения частоты каждой периодической компоненты от расчетного значения и также включают его в состав диагностического вектора, причем фактическое значение частоты каждой периодической компоненты определяют как среднее значение фактических частот входящих в нее гармоник, приведенных к первой гармонике, с поправкой на коэффициенты коррекции, определяемые видом функции окна преобразования Фурье по формулам:

Δ=F_ру-F_ро,

,

F_iy=F_i0+K_i·dF,

где F_py - фактическое значение частоты выделяемой периодической компоненты;

F_po - расчетное (паспортное) значение частоты выделяемой периодической компоненты;

F_iy - фактическое значение частоты i-ой гармоники выделяемой периодической компоненты;

F_i0 - центральная частота полосы спектра, в которой находится фактическое значение частоты i-ой гармоники выделяемой периодической компоненты;

dF - ширина единичной полосы спектра БПФ преобразования;

К_i - коэффициент коррекции i-ой гармоники, определяемый видом функции окна взвешивания Ханна, используемого при преобразовании Фурье;

U_i0 - амплитуда максимальной составляющей спектра в окрестности i-ой гармоники;

U_i1 - амплитуда соседней боковой составляющей, имеющей меньшую частоту (расположенную слева от максимальной);

U_i2 - амплитуда соседней боковой составляющей, имеющей большую частоту (расположенную справа от максимальной);

i - номер гармоники периодической компоненты.