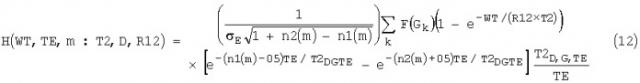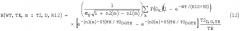Анализ ямр-данных многократных измерений на основе максимальной энтропии

Анализ ямр-данных многократных измерений на основе максимальной энтропии

Иллюстрации

Показать все

Реферат

Перекрестные ссылки на родственные заявки

Настоящее изобретение заявляет приоритет в соответствии с § 119 раздела 35 Кодекса законов США предварительной патентной заявки США №60/439873 от 14 января 2003 г. Таким образом, упомянутая предварительная заявка целиком включена в настоящее описание посредством ссылки.

Область техники

Настоящее изобретение относится в основном к технологии каротажа на основе ядерного магнитного резонанса (ЯМР). В частности, изобретение относится к способу анализа данных, полученных методом ЯМР (ЯМР-данных), на основе принципа максимальной энтропии.

Предшествующий уровень техники

Существуют различные алгоритмы обратного преобразования, используемые для анализа данных каротажа скважин на основе ядерного магнитного резонанса. Самые первые способы давали одномерные распределения T2 (время поперечного затухания) на основе данных однократных измерений в предположении множественных экспоненциальных затуханий. К упомянутым способам относятся, например, схема "Весовой обработки", предложенная Фридманом, (патент США №5291137) и способ "однородной штрафной функции" (Borgia, G.C. Brown, R.J.S. and Fantazzini, P., J. Magn Reson. 132, 65-77, (1998)). Затем предлагались схемы регистрации данных, содержащие многократные измерения с разными значениями времени ожидания. Тогда же предложены способы обработки данных для анализа результатов этих измерений. Один из этих способов предложен Фридманом (патент США 5486762).

Недавно реализованы комплексные пакеты программ регистрации ЯМР-данных посредством многократных измерений с разными значениями времени ожидания и интервалами между эхо-сигналами. Для обработки этих данных предложены способы обращения прямого моделирования, такие как MACNMR (доклад Slijkerman, W. F. J. et al. SPE 56768, представленный на ежегодной конференции Общества инженеров нефтяников (SPE), Хьюстон, 1999 г.), и способ определения характеристик магниторезонансных флюидов (MRF) (Freedman, патент США №6229308). Способ MRF использует установленные физические закономерности, которые эмпирически калибруются с учетом ЯМР-откликов скважинных флюидов. При использовании реалистических моделей флюидов способ MRF допускает сокращение числа подгоняемых параметров, которые должны быть совместимыми с информационным содержанием характерных данных каротажа на основе ЯМР. Поскольку параметры модели заданным образом связаны с объемами и свойствами отдельных флюидов, то определение значений параметров (т.е. аппроксимация данных) дает оценки искомых петрофизических величин.

Способ прямого моделирования зависит от достоверности используемых моделей флюидов. В "неидеальных" условиях, когда ЯМР-отклики флюидов расходятся с поведением модели (пропитанные нефтью породы, ограниченная диффузия), точность методов может снижаться. В ряде случаев о "неидеальности" откликов можно судить по неудовлетворительному качеству аппроксимации, и тогда модели флюидов можно корректировать путем изменения соответствующего параметра модели. Однако не всегда очевидно, какой из элементов модели флюида должен быть изменен, и эта процедура может быть неэффективной, особенно для неспециалиста.

Для новых измерительных схем, например схем с "редактированием диффузии" (DE), в которых ЯМР-данные по существу ортогонализованы по отношению к релаксации и ослаблению диффузии, предложен способ обработки данных на основе ядра разделяющихся откликов (Venkataramanan, L., Song, Y-Q., and Hurlimann, M., - патент США №6462542). Этот способ не предполагает использования какой-либо модели для различных откликов флюидов. Вместо этого способ заключается в анализе данных на основе несмещенных распределений значений времени релаксации и скорости диффузии. Способ привлекает тем, что он не требует априорного знания свойств флюидов и в благоприятных случаях дает простые графические результаты, которые легко интерпретируются даже неспециалистами. Потенциальный недостаток обратного преобразования заключается в том, что его точность частично зависит от разделимости ядер откликов. Это может ограничить область его применения измерениями, при которых ЯМР-отклик по существу ортогонализирован по каждой размерности измерения, например, применением способа к кратным последовательностям CPMG (по именам авторов - Carr, Purcell, Meiboom, и Gill) с разными интервалами между эхо-сигналами.

Кроме того, существующие способы обработки налагают условие неотрицательности на амплитуды отдельных распределений и обычно требуют выбора, по меньшей мере, одного параметра регуляризации (сглаживания). Из-за условия неотрицательности, имеющего очевидные физические основания, упомянутые алгоритмы обработки становятся, по сути, нелинейными. В принципе, это не составляет проблемы, но требует стабильности от выбранной процедуры оптимизации, поэтому следует проявлять осторожность, чтобы обеспечить приемлемую повторяемость результатов обратного преобразования для данных с шумами. Проблему шумов решают путем использования параметра регуляризации, что обеспечивает сглаживание результирующих распределений. Однако выбор соответствующего значения параметра регуляризации является нетривиальной задачей. Несмотря на множество опубликованных работ, касающихся теоретических аспектов проблемы регулиризации (см., например, ссылки, приведенные в работах Borgia, G.C. Brown, R.J.S. and Fantazzini, P., J. Magn Reson. 132, 65-77, (1998) и Venkataramanan, L., Song, Y-Q., and Hurlimann, M., - патент США №6462542), на практике регуляризация остается в значительной степени субъективной, иногда основанной только на внешнем виде вычисленных распределений. Регуляризация особенно важна при многомерных обратных преобразованиях, поскольку объем данных далеко не достаточен для определения распределения и из-за этого вполне вероятно появление шумовых артефактов. Кроме того, различные области распределений показывают сильные различия чувствительности к входным данным. Недоучет упомянутых колебаний чувствительности может привести к появлению ложных или нереальных пиков в распределениях, при интерпретации которых легко сделать ошибку.

Сущность изобретения

В соответствии с одним аспектом сущности изобретения предлагается способ извлечения информации о системе ядерных спинов из данных, полученных на образце толщи пород. В частности, регистрируют множество ЯМР-данных для образца флюида либо в скважине, либо в лабораторных условиях. По множеству ЯМР-данных вычисляют многомерное распределение с использованием математического обратного преобразования, которое не зависит от априорного знания свойств образца флюида.

В соответствии с другим аспектом сущности изобретения вычисляют многомерное распределение с использованием математического обратного преобразования, которое не зависит от априорного знания свойств образца флюида и не зависит от конкретной последовательности регистрации данных.

Краткое описание чертежей

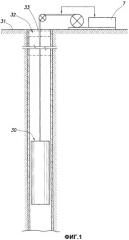
Фиг.1 - схематичное представление примера скважинной системы регистрации ЯМР-данных.

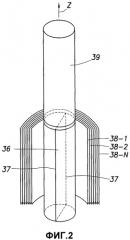
Фиг.2 - более подробное схематичное представление системы по фиг.1.

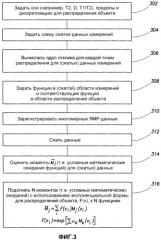
Фиг.3 - схема последовательности этапов предлагаемого способа.

Фиг.4 - набор графиков для интерпретации, построенных по данным, обработанным в соответствии с предложенным способом.

Фиг.5 - второй набор графиков для интерпретации, построенных по данным, обработанным в соответствии с предложенным способом.

Фиг.6 - сравнение данных, представленных на фиг.4 и 5.

Фиг.7 - еще один набор графиков для интерпретации, построенных по данным, обработанным в соответствии с предложенным способом.

Таблица 1 - последовательность регистрации данных прибором CMR с использованием измерений по схеме CPMG.

Таблица 2 - параметры, используемые для 3-мерного обратного преобразования ЯМР-данных многократных измерений.

Таблица 3 - Параметры моделирования, использованные для тестирования обратного преобразования на основе МЕР.

Подробное описание предпочтительного варианта осуществления изобретения

В принципе предложен способ обработки, обеспечивающий непротиворечивую обработку ЯМР-данных многократных измерений для получения относительно несмещенных многомерных распределений, которые можно использовать для определения параметров ЯМР-откликов флюидов или в качестве основы для непосредственного прогнозирования геологического разреза.

Способ обработки многомерных данных на основе принципа максимальной энтропии (МЕР) преодолевает ограничения способов с разделяющимися ядрами и выполняет регуляризацию простым систематическим методом без необходимости ввода данных пользователем и независимо от уровней шумов в данных или характера составляющих основу распределений. Этот способ обеспечивает простое графическое представление данных, которые можно использовать для определения откликов флюидов в любых условиях. Графические представления (т.е. многомерные распределения) можно использовать непосредственно для интерпретации или альтернативно их можно использовать как руководство при выборе параметров для обработки данных путем моделирования, например, способом MRF. Важно сознавать, что способ на основе МЕР, а также способы интерпретации диаграмм D-T2 применимы к схемам измерения CPMG и DE или любой схеме измерения методом ЯМР (ЯМР-измерения), которые чувствительны к скоростям спиновой релаксации, к молекулярной диффузии и сочетанию этих свойств.

Отклик А при трехмерном измерении можно выразить следующим уравнением

где τ₁, τ₂, τ₃ - три параметра регистрации данных, которые характеризуют конкретное измерение, f(i,j,k) - амплитуда компоненты i, j, k в 3-мерном распределении (т.е. каждое распределение соответствует конкретному свойству), H(τ₁,τ₂,τ₃;i,j,k) - отклик этой компоненты на измерение, заданное параметрами τ₁, τ₂, τ₃, а δ - случайный шум. Следует отметить, что число измерений в распределении не обязательно должно быть равно числу измерений при регистрации данных. В рассматриваемом контексте в уравнении (1) параметры τ₁, τ₂ и τ₃ могли бы, например, представлять время ожидания (WT), интервал между эхо-сигналами (ТЕ) и время (t) при измерении по схеме CPMG. Аналогично индекс i мог бы относиться к конкретному значению T2, T2(i), j - может относиться к скорости диффузии, D(j), a k могло бы соответствовать конкретному значению Т1 или отношению T1/T2, R12(k).

Решение уравнения (1) состоит в определении f(i,j,k) при наличии серии измерений A(τ₁, τ₂, τ₃) в предположении, что известна форма H(τ₁,τ₂,τ₃;i,j,k). На первый взгляд это может показаться простой задачей, так как в последовательности многократных ЯМР-измерений обычно регистрируют несколько тысяч эхо-сигналов, в то время как для описания распределения может быть достаточно приблизительно 20×20×10=4000 компонентов. Иначе говоря, число замеров (т.е. амплитуд эхо-сигналов) сравнимо с числом компонент распределения или превосходит это число. На практике обратное преобразование, описываемое уравнением (1), является в значительной степени недоопределенным, поскольку ядра откликов H(τ₁,τ₂,τ₃;i,j,k) по существу линейно зависимы. Фактически даже полные данные многократных измерений с высоким отношением сигнала к шуму часто можно описать всего 10 параметрами, а это означает, что данные можно сжать всего до 10 независимых компонент без существенной потери информации.

Проблема получения расширенных распределений на основе ограниченных множеств данных возникает во многих научных областях. Одним из соответствующих полезных и актуальных примеров является определение функций молекулярного распределения. При этом в наличии может быть небольшое число (иногда всего один) измеренных моментов распределения, по которым требуется вычислить все распределение. Теория информации (Е.Т.Jaynes, Phys. Rev. 106, 620 (1957)) утверждает, что в таком случае "наиболее вероятное" распределение имеет вид

где Z - функция нормирования, M_n(x_i) - функции, математические ожидания которых определяют моменты,

α_n - параметры, которые подгоняют так, чтобы моменты, вычисленные с использованием уравнений (2) и (3), соответствовали измеренным значениям. Число параметров α_n, используемых для аппроксимации данных, не должно превышать число измеренных моментов. В отличие от традиционных алгоритмов обратного преобразования, обычно применяемых для получения распределений Т2, предлагаемая схема не требует явной регуляризации. Предлагаемый способ дает распределение, которое одновременно согласуется со всеми доступными данными и обладает максимальной энтропией S, выраженной уравнением

где k - постоянная величина. Простое изложение "принципа максимальной энтропии" (МЕР) применительно к функциям распределения приведено в недавно выпущенной книге - Dill, К. А. and Bromberg, S., "Molecular Driving Forces", Garland Science Publishing, (2003).

Более специальный вывод приведен также в большинстве обычных учебников по статистической термодинамике (например, McClelland, B.J., "Statistical Thermodynamics", Chapman and Hall, (1973)) в рамках изложения статистики Максвелла-Больцмана. В этом случае "измеренной" величиной является энергия Е

и результирующее общеизвестное распределение имеет вид

где β=1/kT (T = температура в градуса К), a E_i - энергия состояния i.

Хороший пример практического применения МЕР приведен в работе Catalano, D., Di Bari, L., Veracini, С., Shilstone, G. and Zannoni, C., J. Chem. Phys., 94, 3928, (1991), где описан вывод функций внутреннего ротамерического распределения для замещенных молекул бифенила по результатам ЯМР-измерений дипольной связи.

Принципы максимальной энтропии можно также распространить на вывод распределений времени релаксации и скорости диффузии по данным каротажа скважин на основе ЯМР. По меньшей мере, одно отличие заключается в применении этого принципа не к одномерным, а к многомерным распределениям. Как показано в настоящем описании, предложенный способ на основе МЕР позволяет обрабатывать такие многомерные распределения, которые, как полагают, в ином случае будут в значительной степени недоопределенными с помощью доступных данных.

Первый этап применения МЕР состоит в том, чтобы определить подходящее множество базисных функций (т.е. M_n(x_i)), заданных в области распределения (например, в области Т2-D), средние значения которых поддаются измерению. Желательно (но не обязательно), чтобы базисные функции были ортогональными и чтобы их можно было классифицировать по степени "детальности" их содержания. Иначе говоря, предполагается, что простые распределения с небольшим числом широких максимумов должны определяться небольшим числом первых моментов. Одно множество функций, которое соответствует этим требованиям, можно получить сингулярным разложением (SVD) ядра измерений, H(τ₁,τ₂,τ₃;i,,j,k). Способ на основе SVD разлагает ядерное ядро, Н, на произведение трех отдельных матриц

где S - диагональная матрица, в которой элементы s_i являются сингулярными точками Н. Столбцы U и V известны как соответственно левый и правый сингулярные векторы и ортогональны между собой,

Чтобы выразить H в виде 2-мерной матрицы, определяем общую координату измерения τ (например, τ=WT, ТЕ(L), n) и координату распределения х (например, х=Т2, D, R12). Тогда из уравнения (7) можно вывести

где ν_n - ненормированные ортогональные векторы в области (х) функции распределения. Объединение уравнений (1) и (9) приводит к полезному выражению

Поскольку можно получить анализом Н методом SVD, а A(τ) как раз означает измеренные амплитуды эхо-сигналов, то вычисление является простой задачей. Следует отметить, что вторая часть уравнения (10) формально идентична уравнению (3). Следовательно, с точностью до некоторого статистического уровня шумов δ_n можно измерить множество моментов функции распределения f(х), которые не зависят от любого другого момента внутри упомянутого множества. Известно, что в соответствии с анализом SVD эти моменты соответствуют математическим ожиданиям множества ортогональных функций координаты распределения х. Из вышеизложенного описания способа МЕР следует, что функцию распределения можно выразить в виде

где параметры α_n подгоняют так, чтобы воспроизводились измеренные моменты (см. уравнение (10)). Число компонентов N, входящих в экспоненциальное суммирование в правой части уравнения (11), не должно превышать число достоверных измеренных моментов . Число достоверных моментов можно оценить сравнением абсолютных значений моментов с их расчетными стандартными отклонениями. Поскольку моменты склонны к затуханию с ростом ранга n, это сравнительно упрощает задачу определения, при каком значении n моменты становятся несущественными по сравнению с уровнем шумов. Такое определение N резко отличается от обратных преобразований, которые требуют субъективной регуляризации и являются весьма неопределенными. По другому варианту для N можно задать некоторое обоснованное значение, эмпирически определяемое по предыдущим данным или путем моделирования.

Следует отметить, что Z^-1 включено для согласования с принятой индексацией параметра нормирования. Однако в соответствии с одним вариантом осуществления изобретения параметр нормирования совсем опущен. В соответствии с другим вариантом осуществления изобретения параметр нормирования используют посредством приведения уравнения к единичному значению. Далее следует отметить, что хотя описание обратного преобразования дано на основе множества ортогональных функций, ортогональность является простым следствием подхода на основе SVD и не является обязательным условием. Примером анализа, не основанного на SVD, является использование полиномов Лежандра к данным однократных измерений по схеме CPMG. На этом завершается общее теоретическое описание МЕР применительно к получению распределений релаксации и диффузии по ЯМР-данным.

Здесь полезно рассмотреть конкретные формы ядра H и получить соответствующие векторы SVD. При обычной регистрации ЯМР-данных многократных измерений, выполняемых в магнитном поле с напряженностью G, элементы H могут соответствовать амплитуде конкретного эхо-сигнала n, измеренного при времени ожидания (WT) и интервале между эхо-сигналами (ТЕ). Однако в последовательности регистрации данных многократных измерений общее число эхо-сигналов обычно составляет несколько тысяч, а распределение можно определить с помощью нескольких сотен компонент. Очевидно, Н может стать слишком большим и громоздким для целей оценки путем SVD. Поэтому на практике целесообразно (это ограничение связано с располагаемыми возможностями обработки данных, а не с самим алгоритмом) сжимать данные до их численной оценки. Один из простых способов сжатия состоит в вычислении сумм "по окнам". Каждая последовательность эхо-сигналов делится на сегменты (окна), в которых амплитуды эхо-сигналов суммируются (патент США №5291137). Чтобы точно представить множественные экспоненциальные затухания, окна в начальной части последовательности эхо-сигналов обычно содержит малое количество эхо-сигналов, а окна в последних частях последовательности содержат большое количество эхо-сигналов. Для стандартных последовательностей измерений по схеме CPMG с регистрацией данных прибором CMR, который обеспечивает распределение градиентов магнитного поля F(G), ядро суммирования по окнам можно записать следующим образом

где σ_Е - шум в эхо-сигнале для конкретного измерения, γ - протонное гиромагнитное отношение, а n1(m) и n2(m) - первый и последний эхо-сигналы m-ой суммы окна. Отметим также возможность применения других методов сжатия данных (например, SVD). При этом потребуется соответственно изменить результирующее ядро.

Одной целью не зависимого от модели анализа является получение несмещенного представления данных. Информация, содержащаяся в многомерных диаграммах, по существу идентична информации, содержащейся в амплитудах исходных эхо-сигналов. Хотя диаграммы и позволяют представить данные с точки зрения ЯМР, они не обеспечивают петрофизической интерпретации результатов. В ряде случаев петрофизическая интерпретация выполняется совсем просто путем визуального просмотра диаграмм. Однако в некоторых случаях недостаточное разрешение по осям Т1/Т2 или диффузии может воспрепятствовать отождествлению отдельных флюидов, которые дают идентичные значения Т2. Для дальнейшей обработки и получения показателей насыщенности и значений вязкости углеводородов необходимо применить модель к результатам.

Современные многомерные модели (для нефти и воды) отчасти устанавливают, что при каждом значении Т2 коэффициент диффузии может принимать всего два возможных значения, которые соответствуют диффузии воды и нефти. Коэффициент диффузии воды является известной функцией температуры, Т, и не зависит от Т2,

а для нефти коэффициент диффузии находится в линейной зависимости от Т2,

Другими словами, современные решения путем моделирования соответствуют горизонтальным (вода) и диагональным (нефть) линиям на диаграмме зависимости D от T2. При стандартном анализе исходные данные аппроксимируют непосредственно с использованием ограничений, установленных уравнениями (14)-(15). Другой подход заключается в использовании самих диаграмм в качестве входной информации для получения решения. Поскольку информация, содержащаяся в диаграммах, по существу идентична информации, содержащейся в исходных данных, то оба способа решения должны быть эквивалентными. На практике данным часто недостает информации о диффузии (т.е. разрешения), и тогда возникает проблема в повторном назначении различным пластовым флюидам разброса по амплитуде по оси диффузии на диаграмме D-T2. Простой приближенный способ решения этой задачи заключается в том, чтобы использовать среднюю геометрическую скорость диффузии для каждого значения Т2-D_LM(T2), вычисленного по диаграммам, и повторно назначить амплитуду для этого Т2 в соответствии с модельными значениями D для воды и нефти. Кажущееся значение водонасыщенности удобно задавать при каждом значении T2, SXO(T2),

После этого можно получить отдельные распределения T2 для воды и нефти, F_H20, и F_OIL,

Следует отметить, что для вычисления объемов отдельных флюидов можно применить другие схемы. Например, можно проинтегрировать отдельные участки графика, относящиеся к флюиду конкретного типа, чтобы получить соответствующие объемы, по которым затем можно вычислить значения насыщенностей.

На фиг.1 показано устройство для исследования толщ пород 31, пересеченных скважиной 32, которое можно использовать в практических вариантах осуществления способа по настоящему изобретению. Исследовательское устройство или каротажное устройство 30 подвешивают в скважине 32 на бронированном кабеле 33, длина которого по существу определяет относительную глубину устройства 30. Длину кабеля регулируют с помощью подходящего наземного устройства, например барабана и лебедки (не показаны). Наземное оборудование 7 может быть оборудованием обычного типа и может содержать подсистему процессора и обмениваться данными со скважинным оборудованием.

Каротажное устройство, которое выполняет измерения, может быть любым устройством каротажа методом ЯМР, подходящим для применения по методу каротажа на кабеле, как показано выше, или устройством такого типа, который можно применять для измерений в процессе бурения. Устройство 30 содержит, например, средство формирования статического магнитного поля в толще пород и антенное средство радиочастотного (РЧ) диапазона для формирования импульсов РЧ магнитного поля в толще пород и приема спиновых эхо-сигналов из толщи пород. Средство формирования статического магнитного поля может содержать, например, постоянный магнит или группу магнитов, а антенное средство РЧ диапазона для формирования импульсов РЧ магнитного поля и приема спиновых эхо-сигналов из толщи пород может содержать, например, одну или несколько РЧ антенн.

В варианте осуществления изобретения используют набор измерений, выполняемых устройством каротажа методом ЯМР, которое может обеспечивать получение отдельных измерений от множества близко расположенных тонкослойных участков в окружающих толщах пород. На фиг.2 показаны в упрощенном виде некоторые компоненты каротажного устройства 30 подходящего типа. На этом чертеже показаны первый центральный магнит или группа магнитов 36 и РЧ антенна, обозначенная 37, которая может быть выполнена в виде соответственно ориентированной катушки или катушек. На фиг.2 изображены также в общем виде близко расположенные цилиндрические тонкослойные участки, 38-1, 38-2...38-N, которые могут селектироваться по частоте с использованием многочастотного каротажного устройства того типа, как упомянутое в ссылках. Как известно из уровня техники, например, каротажное устройство по патенту США №4710713 может выделять исследуемый тонкослойный участок посредством соответствующей частотной селекции энергии излучаемых РЧ импульсов. Кроме того, на фиг.2 позицией 39 обозначены магнит или группа магнитов, которые могут использоваться для формирования предварительно поляризующего статического магнитного поля в толщах пород, к которым приближается зона, обследуемая каротажным устройством по мере его подъема по скважине в направлении стрелки Z. В связи с вышеизложенным можно упомянуть, например, патент США №5055788. См. также патент США №3597681.

На фиг.3 показана примерная схема последовательности этапов в соответствии с предлагаемым вариантом осуществления изобретения. Вначале, на этапе 302, назначают значения для координатных осей и пределы. Эти оси будут использоваться для окончательного формирования многомерного графика результатов решения задачи обратного преобразования. Например, в соответствии с одним вариантом осуществления изобретения задают оси координат диффузии и релаксации Т2, по которым должны отображаться ЯМР-данные. Как ранее упомянуто, можно использовать другие значения координатных осей, например заменить ось Т2 осью Т1/Т2 или R12, или графиками в осях координат Т2-Т1 или Т2-R12. Кроме того, при формировании распределения объекта применяют дискретизацию. Дискретизация обычно заключается в определении разрешения по каждой размерной оси. Например, для упрощения анализа разрешение по каждой оси обеспечивают заданным числом значений в логарифмическом или линейном масштабе. На этапе 304 задают схему сжатия. Этот этап бывает необходим в основном по причине ограниченных вычислительных возможностей. Однако способ на основе МЕР сам по себе способен работать со сжатыми данными или с полным множеством данных. Таким образом, этап 304 будет необязательным при наличии достаточных вычислительных возможностей. Одним из примеров схемы сжатия является вышеупомянутое суммирование по окнам. Однако можно применить многие другие схемы сжатия без изменения способа на основе МЕР.

На следующем этапе 306 вычисляют ядро отклика для каждой точки данных в распределении объекта. Уравнение 12 является одним из примеров уравнения ядра откликов. В частности, H(WT/,TE,m:T2,D,R12) определяют при каждом значении T2,D,R12 для каждого эхо-сигнала (или в случае сжатия с использованием окон, для каждой суммы эхо-сигналов окна). На этапе 308 соответствующие функции задают как в области измерений, (WT, ТЕ, t), так и в области распределений объекта, (Т2, D, R12) уравнение 1.

Регистрацию ЯМР-данных выполняют на этапе 310. Однако хронирование регистрации можно изменять в широких пределах. Например, регистрация данных может быть выполнена во время некоторого предварительного каротажного цикла, либо данные можно регистрировать по алгоритму на основе МЕР во время каротажного цикла. Кроме того, регистрацию данных можно выполнять с помощью любого числа приборов регистрации ЯМР-данных, например прибора на кабеле, прибора для каротажа в процессе бурения, прибора для пробоотбора флюидов, переносного или лабораторного прибора. Кроме того, способ на основе МЕР не зависит от используемой последовательности регистрации и может быть применен, например, с данными, полученными в ходе последовательностей измерения по схеме CPMG, измененной схеме CPMG или схеме с редактированием диффузии.

На этапе 312 множество данных сжимают по схеме сжатия, выбранной на этапе 304. На этапе 314 моменты M_j в области измерений (области спиновых эхо-сигналов) оценивают по ЯМР-данным или сжатым данным. Этот этап или в соответствии с другим вариантом отдельный этап включает в себя определение числа N значимых моментов. В соответствии с другим вариантом пренебрегают предварительно заданным множеством N достоверных моментов. На данном этапе можно отбросить более высокие моменты. На этапе 316 одновременно аппроксимируют N моментов M_j в области измерения с использованием алгоритма оптимизации, который обеспечивает независимую подгонку N параметров. Этими N подгоняемыми параметрами являются весовые коэффициенты, связанные с каждой из N функций, которые были заданы в области распределения объекта на этапе 308. Значения этих N параметров вместе с соответствующими им функциями задают полную функцию распределения объекта в соответствии с экспоненциальным выражением для суммы. Окончательной оценкой для (много)мерного распределения является такая оценка, для которой N вычисленных моментов наиболее точно соответствуют N измеренным моментам.

Применение обратного преобразования на основе МЕР

Чтобы оценить H, сначала необходимо задать последовательность регистрации данных. Например, рассмотрим типичную регистрацию данных для магниторезонансных флюидов (MRF), состоящую из 6 измерений по схеме CPMG. Последовательность регистрации данных приведена в таблице 1. Следует отметить, что эта последовательность содержит измерения с разными интервалами между эхо-сигналами и разными значениями времени ожидания. ЯМР-отклик модулируется по Т2, R12 (или Т1) и D, поэтому соответствующее преобразование является 3-мерным. Теперь следует выбрать пределы для осей распределения и число компонентов по каждой оси. Следует выбрать достаточное число компонентов, чтобы адекватно описать каждый из разных откликов, при условии что число измерений обеспечивает различение этих откликов, и чтобы при этом общее число компонентов было достаточно малым для обеспечения эффективных вычислений. Параметры обратного преобразования, используемые в данном примере, приведены в таблице 2. Схема дискретизации не оптимизировалась. Однако окончательные результаты обратного преобразования в разумных пределах сравнительно мало связаны с особенностями дискретизации.

1. Синтезированные данные

Чтобы продемонстрировать обработку данных, представлены четыре примера синтезированных данных. Данные сформированы для показанной в таблице 1 последовательности регистрации, использующей 1 компонент (тесты 1 и 2) или 2 компонента (тесты 3 и 4), каждый с единственными значениями Т2, D и R12. Полная амплитуда сигнала была установлена на значение 0,20 В/В, а в последовательность эхо-сигналов добавлен случайный шум с уровнем 0,01 В/В. Параметры моделирования представлены в таблице 3.

Результаты проверок обратного преобразования приведены на фиг.4-7. Фиг.4 иллюстрирует применение способа на основе МЕР в соответствии с условиями теста 1. График 402 показывает синтезированные ЯМР-данные спиновых эхо-сигналов и аппроксимацию взвешенных сумм, полученных из этих данных. Как показано на оси у, ЯМР-данные сжимают методом суммирования по окнам. График 404 построен на основе приведенных на графике 402 данных о спиновых эхо-сигналах после обработки по способу на основе МЕР. Ось у задается значениями диффузии, а ось х задается значениями Т2, и следовательно, в данном случае построен график D-T2. График D-T2 получают путем суммирования по третьему измерению (R12=T1/T2). Максимум 405 на графике 404 отражает вероятное присутствие флюида (нефти, воды или газа). На нижнем левом графике 406 показано сравнение интегрированного распределения Т2, обозначенного позицией 410, с входным распределением 408. На верхнем правом графике 412 показано сравнение интегрированного распределения D, обозначенного позицией 416, с входным распределением 414. Единственный максимум 405 точно представлен как по оси Т2, так и по оси D. Для высококачественной аппроксимации данных потребовалось всего 12 функций SVD (с точностью до статистического уровня шумов).

На фиг.5 представлены результаты теста 2. Это моделирование идентично тесту 1 за исключением отношения Т1/Т2, R12, которое в тесте 2 увеличено до 2. Верхний левый график 503 является графиком T2-D, полученным суммированием по третьему измерению (R12=T1/T2). На нижнем левом графике 507 показано сравнение интегрированного распределения Т2, обозначенного позицией 502, с входным распределением 504. На верхнем правом графике 509 показано сравнение интегрированного распределения D, обозначенного позицией 506, с входным распределением 508. И снова, единственный максимум 505 точно представлен как по оси Т2, так и по оси D. Наблюдается небольшое снижение разрешения по оси D по сравнению с результатами теста 1. Это может быть статистическое отклонение из-за различия в реализации шумов в двух случаях моделирования. И снова, для аппроксимации данных потребовалось всего 12 функций SVD.

На фиг.6 сравниваются распределения Т1 и Т2, вычисленные для тестов 1 и 2. Для теста 1 с заданным значением R12=T1/T2=1 вычисленные распределения Т1 и Т2 точно совмещаются, как показано на графике 602. Напротив, в тесте 2, показанном на графике 604, где использовано значение R12=T1/T2=2, вычисленное распределение Т1, обозначенное позицией 608, имеет центр в точке ˜ 2 seconds, приблизительно в 2 раза выше, чем распределение Т2, обозначенное позицией 606. Это указывает на способность обратного преобразования точно определять значения Т1. Следует отметить, что пределы, в которых можно точно определять значения Т1, зависят от выбора значений времени ожидания в программе регистрации данных.

Результаты 2-мерного обратного преобразования на основе МЕР данных 702, зарегистрированных по схеме редактирования диффузии в толще нефтеносного песчаника, представлены на фиг.7. Вверху слева показан график T2-D. Показано, как пересекаются линии для откликов воды (горизонтальная линия 704) и дегазированной нефти (слабо поднимающаяся линия 706). Нижний левый график является интегральным распределением Т2. Верхний правый график является интегральным распределением D. Последовательность в схеме редактирования диффузии содержала 10 измерений с большими интервалами между эхо-сигналами, от 2 мс до 12 мс. Для всех измерений использовалось одинаковое время ожидания, так что в данном случае обратное преобразование было 2-мерным (т.е. Т2, D). Видно, что в данном случае регистрации данных по схеме редактирования диффузии обратное преобразование на основе МЕР точно разрешает два примера флюидов 708 и 710 как в области