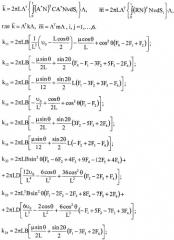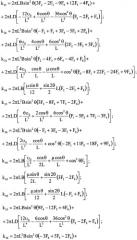Способ усиления механических колебаний при помощи волновода, выполненного в виде конической оболочки вращения

Способ усиления механических колебаний при помощи волновода, выполненного в виде конической оболочки вращения

Иллюстрации

Показать все

Реферат

Изобретение относится к способам повышения уровня механических колебаний без наличия редукторов и эксцентриков и может быть использовано в приборостроении для создания вибростендов.

Существует способ создания вибростендов, основанный на возбуждении колебаний упруго-опертой платформы при помощи электромагнитов (см. патент US 2003/0229438 A1 G06F 17/00) и принятое за прототип.

К причинам, препятствующим достижению указанного ниже технического результата при применении известного способа возбуждения колебаний, принятого за прототип, относятся: невозможность усиление и передачи колебаний в диапазоне ультразвука при малой амплитуде возбуждения.

Технический результат - усиление высокочастотных колебаний в диапазоне ультразвука с амплитудой возбуждения порядка нескольких микрометров, создаваемых магнитострикционным или электромагнитным устройством.

Особенность заключается в том, что меняя параметры волновода, а именно угол раствора конуса и толщину оболочки, получаем требуемое усиление колебаний, минуя различные промежуточные устройства.

Сущность изобретения заключается в следующем: на широкое основание круговой конической оболочки подается высокочастотный сигнал с закрепленного на нем магнитострикционного или электромагнитного устройства, при этом на противоположном конце оболочки получаем усиленные колебания той же частоты, уровень которых рассчитывается согласно схеме, описание которой приводится в работе Санкин Ю.Н., Трифанов А.Е. Осесимметричные колебания оболочек вращения при внезапном нагружении // ПММ. Том 66, вып.4, 2002, с.608-616.

Уравнения гармонических колебаний оболочки вращения могут быть записаны в виде, см.: Фридман В.М., Чернина B.C. Видоизменение метода Бубнова-Галеркина-Ритца, связанное со смешанным вариационным принципом в теории упругости. - Известия АН СССР, МТТ, №1, 1969, с.64-78:

где х^Т=|T₁, T₂, S, M₁, M₂, H| - вектор усилий Т₁, М₁ и Т₂, М₂ - меридиальные и окружные растягивающие усилия и изгибающие моменты; S₁₂, S₂₁, H₁₂, H₂₁ - касательные усилия и крутящие моменты; у^T=|u, v, w| - вектор перемещений; u - перемещение по касательной к меридиану, v - перемещение по касательной к параллели; w - нормальное перемещение; f^T=|q₁, q₂, q_n| - вектор внешней нагрузки; q₁, q₂, q_n соответствуют по направлению составляющим вектора перемещений; R - масса, приходящаяся на единицу площади срединной поверхности оболочки, ω - частота вынужденных колебаний,

R₁, R₂ - главные радиусы кривизны; υ - радиус кривизны параллели;

В=Eh/(1-μ²) - жесткость при растяжении; D=Eh³/12(1-μ²) - цилиндрическая жесткость при изгибе; Е - модуль упругости; μ - коэффициент Пуассона; h - толщина оболочки. Операторы А и А^* обладают свойством:

где σ - поверхность оболочки. При вычислении интеграла (2) учтена периодичность по углу θ. Здесь соответственно векторы обобщенных сил и перемещений на краях элемента, структура операторов А и А^* дана в работах. Уравнения (1) следует дополнить соответствующими граничными условиями, которые следуют из свойств операторов (2),

Здесь Г₁ - часть контура, где заданы усилия; Г₂ - часть контура, где заданы перемещения. Деление граничного контура на Г₁, Г₂ считается условным, так как на одном и том же участке могут быть заданы отдельные компоненты вектора обобщенных сил и дополнительные компоненты вектора перемещений.

Решение таким образом поставленной задачи сообщает функционалу

стационарное значение.

Второй интеграл в выражении функционала (4) является работой граничных усилий и конструируется согласно (2).

Для конической оболочки (Фиг.1), когда R₁=∞, при осесимметричной нагрузке величина, связанная с перемещением v, не рассматривается, а операторы А^* и С преобразуются к виду:

где dS=υdϕ.

Зададимся полем перемещений в виде: u=α₁+α₂S, w=α₃S+α₄S+α₅S²+α₆S³, где α₁, ..., α₆ - неизвестные коэффициенты.

Такое представление может быть оправдано тем, что, например, для цилиндрической оболочки уравнение изгиба не связано с уравнением растяжения и эта зависимость мала при относительно малых θ и малой длине элемента. Найдем функции формы. Функции формы определяются согласно соотношению U=NU_ij, где U^T=|u w|, u_i, w_i, γ_i, u_j, w_j, γ_j - перемещения и углы поворота краевых сечений. N₁, ..., N₆ - функции формы.

Введем переменную где L - длина элемента по образующей. Тогда получим [5]: N₄=S₁,

При переходе от местной системы осей к единой (X, Y, Z), выражая вектор у через матрицу функций формы N и узловые перемещения

z^Т=|u_i, w_i, dw_i/dS, U_j, w_j, dw_j/dS|,

функционал (4) перепишется в виде:

где

Учитывая, что dσ=2πLdS, получим для матриц жесткостей и масс следующие выражения:

Для формирования глобальной матрицы представим матрицу жесткости и матрицу разбитой на блоки 3×3:

а вектор нагрузки f^Т=|f_ij, f_ji|. Тогда для оболочки получим следующее рекуррентное соотношение, подобное аналогичному соотношению для балок:

где k - номер характерного сечения, f_k - вектор нагрузки в сечении k.

Для того чтобы учесть рассеяние энергии, подставим вместо Е величину E(1+iγ) в уравнения (5), где γ - коэффициент внутреннего рассеяния энергии, и решая систему уравнений (5), строим амплитудно-фазочастотные характеристики АФЧХ (Фиг.2). Математическая, модель оболочки вращения формируется по характерным точкам АФЧХ в виде:

где k_j=A_jT_1j/T_2j - коэффициент усиления j-ого колебательного звена; А_j - вертикальный размер витка АФЧХ; Т_1j=T_2j(1-ω² _2j/ω² _1j) - постоянная времени демпфирования; Т_2j=1/ω_1j - инерционная постоянная; ω_1j - резонансная частота, соответствующая максимуму мнимой части АФЧХ;

ω_2j - частота, соответствующая максимуму действительной части АФЧХ;

ω - частота колебаний; i - мнимая единица,

после чего определяется частота возбудителя магнитострикционных или электромагнитных колебаний, обеспечивающая на выходе максимальную амплитуду усиливаемых колебаний.

Формула (6) получена в работе Санкин Ю.Н. Динамические характеристики вязкоупругих систем с распределенными параметрами. Саратов, изд-во СГУ, 1977, 309 с. Формулы для Т_1j и T_2j приведены в работе Санкин Ю.Н. Малые колебания механических систем с одной степенью свободы. Ульяновск, изд во УлГТУ, 1991, 36 с.

Известен волновод, выполненный в виде конического стержня сплошного сечения. Недостатком, препятствующим выполнению поставленной задачи, является значительная погонная масса стержня, малая площадь сечения, к которому прикладывается возмущающее воздействие, что существенно ограничивает мощность передаваемого сигнала, а также наличие больших потерь на внутреннее трение, что не позволяет создавать высокочастотные вибростенды, необходимые для проверки работоспособности оборудования в условиях мощного высокочастотного звукового поля.

Способ усиления механических колебаний при помощи волновода, выполненного в виде конической оболочки вращения, отличается тем, что в качестве волновода используют тонкостенную круговую коническую оболочку, на широкое основание которой подают высокочастотный сигнал с закрепленного на ней магнитострикционного или электромагнитного генератора механический колебаний, причем частоту возбуждения выбирают при помощи математической модели поведения оболочки на выходе, определяемой по формуле (6) на частоте ω, когда амплитуда колебаний на выходе оказывается максимальной. Предлагаемая конструкция свободна от вышеуказанных недостатков, т.к. радиус сечения оболочки, где прикладывается возмущающее воздействие, может быть выбран достаточно больших размеров в зависимости от величины передаваемой мощности. Также из соображений минимизации потерь на внутреннее трение устанавливается толщина оболочки (Фиг.3), где 1 - приборный отсек, 2 - коническая оболочка, 3 - вибратор, выполненный из магнитострикционного материала, 4 - катушка для возбуждения колебаний, ЗГ - звуковой генератор.

Ниже приводится зависимость выходного сигнала от радиуса входного сечения (Фиг.4), где сплошной линией показан выходной сигнал конической оболочки радиуса 0.25 м и толщиной 5 мм, а пунктирной - радиуса 0.5 м и толщиной 5 мм, и изменение амплитуды в зависимости от толщины стенки (Фиг.5), определяющей потери на внутреннее трение, где сплошной линией показан выходной сигнал конической оболочки радиуса 0.5 м и толщиной 2 мм, а пунктирной - радиуса 0.5 м и толщиной 5 мм.

Способ усиления механических колебаний при помощи волновода, выполненного в виде конической оболочки вращения, отличающийся тем, что в качестве волновода используют тонкостенную круговую коническую оболочку, на широкое основание которой подают высокочастотный сигнал с закрепленного на ней магнитострикционного или электромагнитного генератора механических колебаний, меняя параметры волновода, а именно угол раствора конуса и толщину оболочки, получают требуемое усиление колебаний, минуя различные промежуточные устройства, причем частоту возбуждения выбирают при помощи математической модели поведения оболочки на выходе, определяемой по формуле

,

где k_j=A_jT_1j/T_2j - коэффициент усиления j-ого колебательного звена;

А_j - вертикальный размер витка АФЧХ;

- постоянная времени демпфирования;

- инерционная постоянная;

ω_1j - резонансная частота, соответствующая максимуму мнимой части АФЧХ;

ω_2j - частота, соответствующая максимуму действительной части АФЧХ;

ω - частота колебаний;

i - мнимая единица,

на частоте ω, когда амплитуда колебаний на выходе оказывается

максимальной.