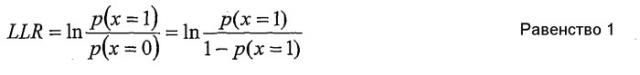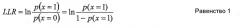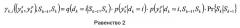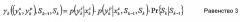Мар декодер локального стирания

Мар декодер локального стирания

Иллюстрации

Показать все

Реферат

ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ

Данное изобретение относится к способу декодирования по меньшей мере одного кодового слова, причем по меньшей мере одно кодовое слово было генерировано кодером, содержащим структуру, обеспечивающую код, представимый множеством переходов от одной ветви к другой в диаграмме матрицы. Далее данное изобретение обеспечивает соответствующий декодер, также как мобильную станцию и базовую станцию в сети связи, применяющей декодер. Кроме того, обеспечена система связи, содержащая базовые станции и мобильные станции.

УРОВЕНЬ ТЕХНИКИ

Кодирование сдвиговых регистров

Сверточные коды и связанные коды могут генерироваться посредством одного или нескольких последовательно включенных или каскадно включенных сдвиговых регистров. Для простоты в следующих разделах рассмотрены двоичные сдвиговые регистры. Двоичные сдвиговые регистры способны принимать значение либо двоичное 0, либо двоичное 1. Когда имеет место сдвиг, содержание каждого регистра передается к последующему регистру и становится его новым содержанием. Обычно ввод в кодер используется как новое содержание первого регистра.

Выход кодера с двоичным сдвиговым регистром обычно получается посредством сложения по модулю 2 содержаний нескольких сдвиговых регистров перед сдвигом. В качестве иллюстрации простой кодер двоичного сдвигового регистра показан на фиг.1, где число сдвиговых регистров r=2 и число состояний М=4. Каждый сдвиговый регистр представлен посредством D, и каждый блок сложения по модулю 2 представлен посредством «+». Два выходных бита получаются из одного входного бита: первый выходной бит идентичен входному биту (верхняя ветвь), тогда как второй выходной бит получается посредством сложения по модулю 2 состояний сдвиговых регистров и входного бита (нижняя ветвь).

На фиг.2 показана диаграмма перехода состояний для кодера из фиг.1. Каждое состояние представлено значениями сдвигового регистра. Каждый переход представлен ориентированным ребром. Переход, вызванный входным битом нуля, обозначен прерывистым ребром, тогда как переход, вызванный входным битом единицы, обозначен прямым ребром. Каждое ребро далее обозначено входным битом, за которым следуют соответствующие выходные биты. Альтернативным представлением диаграммы перехода состояний является матрица, которая составлена из элементов матрицы, как показано на фиг.3. Дополнительные подробности о кодировании сдвиговых регистров (также известном как сверточное кодирование) могут, например, быть найдены в Lin et al., «Error Control Coding: Fundamentals and Applications», Prentice-Hall Inc., chapter 10.

Сдвиговые регистры обычно используются для сверточных кодов. В последнее время, они также использовались в «турбокодах», достигающих очень низких интенсивностей ошибок, что делает их привлекательными для систем связи.

Популярными алгоритмами декодирования для кодов сдвиговых регистров являются, например, алгоритм Витерби и максимальный апостериорный алгоритм. Хотя первый часто используется для традиционных сверточных кодов, последний является очень популярным для декодирования турбокодов из-за их мягкого выхода апостериорной вероятности.

Максимальный апостериорный алгоритм

Краткое описание максимального апостериорного алгоритма обеспечено в следующих абзацах. Для краткости более подробно рассмотрен двоичный случай. Распространение на недвоичный случай не должно создавать проблем для специалистов в данной области техники. Вообще говоря, в недвоичном случае вероятности событий обычно не могут выражаться посредством отношения логарифмического правдоподобия. Вместо этого может использоваться некоторая (возможно логарифмическая) абсолютная вероятностная мера. Очевидно, все равенства, приведенные далее и включающие отношения логарифмического правдоподобия, должны были бы быть изменены таким образом, чтобы они содержали упомянутые абсолютные вероятностные меры.

Упрощающая характеристика двоичного случая состоит в том, что - так как имеется только два возможных события - вероятности событий могут быть выражены в виде отношения логарифмического правдоподобия (LLR), которое обычно определяется следующим образом:

как натуральный логарифм отношения вероятностей того, что х является одним из двух возможных событий.

Следующие символы используются по всему этому документу:

k	Индекс информационного бита
K	Число информационных битов в одном кодированном блоке
r	Число сдвиговых регистров в кодере
М	Число состояний в кодере
Sk	Состояние для индекса k
dk	Информационный бит номер k, либо 0, либо 1, перед кодированием
dk	Информационный бит номер k, либо 0, либо 1, после кодирования
xs k	Систематическое значение для бита dk на выходе кодера, -1 или +1
xp k	Величина четности для бита dk на выходе кодера, -1 или +1
xk=(xs kxp k)	Последовательность систематического значения и величины четности для бита dk на выходе кодера
ys k	Принятое значение для систематического бита k на входе декодера
yp k	Принятое значение для бита четности k на входе декодера
yk=(ys kyp k)	Принятая последовательность систематического бита и бита четности для информационного бита k на входе декодера
γk,I(yk,m',m'')	Вероятность перехода от одной ветви к другой для перехода между состояниями m' и m'', при заданном наблюдении принятого кодового слова yk, при допущении, что информационный бит dk=i (см. объяснение равенства 2)
Гk(yk,m',m'')	Логарифм γk,i
αk(Sk)	Вероятностная мера для пребывания в состоянии Sk для информационного бита k при заданной принятой последовательности y1...yk
βk(Sk)	Вероятностная мера для пребывания в состоянии Sk для информационного бита k при заданной принятой последовательности yk...yK
Li(xs k)	Отношение логарифмического правдоподобия внутренней (априорной) вероятности, которое доступно для бита xs k
Le(xs k)	Отношение логарифмического правдоподобия внешней вероятности, которое вычислено для бита xs k
L(xs k)	Отношение логарифмического правдоподобия вероятности принятия решения (апостериорной вероятности), которое вычислено для бита xs k

Алгоритм имеет два компонента, обычно называемые прямой и обратной рекурсией. Более конкретно, два распределения, α_k и β_k, рекурсивно обновляются. Величина α_k(S_k) представляет вероятностную меру для нахождения в состоянии S_k=m для информационного бита k, при заданной принятой последовательности y₁...y_k. Подобным же образом β_k(S_k) представляет вероятностную меру для нахождения в состоянии S_k=m для информационного бита k при заданной принятой последовательности y_k...y_K.

Обе рекурсии могут быть определены на основе так называемой вероятности перехода от одной ветви к другой γ_k,i(y_k,m',m''). Она представляет вероятность перехода между состояниями m' и m'' при заданном наблюдении принятого кодового слова y_k, в предположении, что информационный бит, вызывающий этот переход, есть d_k=i. Вероятность перехода от одной ветви к другой может быть вычислена как

Значение q(d_k=I|S_k-1,S_k) есть либо один, либо нуль, в зависимости от того, связан ли бит I с переходом из состояния S_k-1 в состояние S_k или нет. Pr{S_k|S_k-1} является априорной вероятностью информационного бита d_k. В контексте турбодекодирования эта вероятность может быть полученной внешней информацией от другого декодера. Другие термины могут быть легко выведены специалистами в данной области техники. Например, если априорная информация не доступна, то вероятности могут быть установлены равными.

Равенство 2 может быть упрощено посредством опускания индекса I, если предполагается, что значения γ существуют только для тех переходов, где q(d_k=I|S_k-1,S_k)=1. С использованием этого предположения равенство может быть переписано как

Рассматривая случай, в котором для каждого информационного бита d_k на входе кодера имеется два кодированных бита x_k=(x^s _kx^p _k) на выходе кодера, равенство 3 может быть далее упрощено с получением скорости кода ½. Кроме того, при рассмотрении двоичного случая равенство 3 может быть далее упрощено посредством использования логарифмических выражений:

В случае двоичного кода сдвигового регистра число состояний М может быть вычислено как

Инициализация

Для каждого перехода от одной ветви к другой, начинающегося в состоянии S_k-1, оканчивающегося в состоянии S_k, вероятность перехода от одной ветви к другой для случая AWGN (аддитивного белого гауссовского шума) BPSK (двоичной фазовой манипуляции) дается следующим образом:

с k, пробегающим от 1 до К.

Поскольку последний член часто используется ниже, равенство 6 может быть переписано как

с использованием

L_c - это масштабный коэффициент канала, который может быть выведен из отношения сигнал-шум (SNR), и в этом случае

с σ², представляющей дисперсию канального шума.

Начальные значения α_k и β_k могут быть инициализированы согласно системным параметрам. Для кода, который начинается и заканчивается в состоянии m=0, инициализации должны быть таковы

и

Прямая рекурсия

Для каждого состояния S_k, k пробегает от 1 до К, α_k может быть вычислено как

Обратная рекурсия

Для каждого состояния S_k, k пробегает от К-1 до 0, β_k может быть вычислено как

Декодирование

Полный процесс декодирования может состоять из применения прямой и обратной рекурсии. После этих рекурсий можно обновить решение мягкого вывода (то есть апостериорную вероятность) каждого информационного бита:

В вышеприведенном равенстве, S⁺ - множество упорядоченных пар, соответствующих всем переходам из одного состояния в другое m'→m'', которые вызваны входом данных d_k=1. S^- определяется подобным образом для d_k=0.

С использованием равенства 15 значение k-го переданного бита может быть рассчитано как

Следует отметить, что внешняя величина L^e, полученная в равенстве 14, может быть использована как внутренняя информация для последующего декодера. Подобным же образом, величина Lⁱ в равенстве 15 может быть получена как внутренняя информация из внешней информации другого декодера.

Специалистам в данной области техники будет ясно, что обе величины могут быть также установлены на правильные значения в случае, если от другого декодера нет доступной информации. Дополнительные подробности о применимости алгоритма к турбокодам, внутренней информации и внешней информации даны в Berrou и др. «Near Shannon Limit Error-Correcting Coding and Decoding: Turbo Codes (1)», Proc.IEEE Int.Conf. On Communications, c. 1064-1070, май 1993.

Max-Log-MAP алгоритм

Для упрощения рассматриваемых вычислений, равенства 12 и 13 могут быть приближены и заменены

и

Подобным же образом искомая переменная может быть получена посредством модификации равенства 14 в

Однако эти приближения могут деградировать эффективность декодирования.

Как будет видно из равенств для прямой и обратной рекурсии, рассматривается информация от бесчисленных величин, которая окончательно выводится из принятого вектора, соответствующего переданному кодовому слову. В шумном окружении канала, высоки шансы того, что несколько принятых величин несут неверную информацию, что означает, что неверная информация может быть получена из этих величин и распространена через итерации декодирования.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Поэтому задачей данного изобретения является уменьшение влияния такой неверной информации.

Эта задача решается содержанием независимых пунктов формулы изобретения. Преимущественные варианты осуществления данного изобретения представлены содержанием зависимых пунктов формулы изобретения.

Согласно одному аспекту данного изобретения не вся информация в прямой и/или обратной рекурсии обрабатывается, как это требовалось бы равенствами соответствующего уровня техники. Согласно этому варианту осуществления данного изобретения некоторые члены вместо этого исключаются. Решение того, какой/какие член/члены исключается/исключаются, может быть, например, определено согласно его/их надежности, то есть член, который создавал бы деградацию эффективности декодирования при использовании в определении прямой и/или обратной рекурсии, опускается в соответствующем равенстве.

В одном из различных примерных вариантов осуществления данного изобретения обеспечен способ декодирования по меньшей мере одного кодового слова, причем по меньшей мере одно кодовое слово было генерировано кодером, содержащим структуру, обеспечивающую код, представимый множеством переходов от одной ветви к другой в диаграмме матрицы.

Согласно этому варианту осуществления этот способ может предусматривать этапы, на которых инициализируют множество вероятностей переходов от одной ветви к другой в декодере на основании принятого кодового слова и структуры кодера, инициализируют первое распределение вероятностей и второе распределение вероятностей согласно начальному состоянию кодера, используемого для кодирования по меньшей мере одного кодового слова, повторно вычисляют значения первого распределения вероятностей на основе начальных значений первого распределения вероятностей и множества вероятностей переходов от одной ветви к другой с использованием рекурсивного алгоритма, повторно вычисляют значения второго распределения вероятностей на основе начальных значений второго распределения вероятностей и множества вероятностей переходов от одной ветви к другой с использованием рекурсивного алгоритма и реконструируют декодированное кодовое слово на основе принятого кодового слова и внешней вероятностной меры, вычисленной на основе множества вероятностей переходов от одной ветви к другой, первого и второго распределения вероятностей.

Либо на каждом, либо на обоих этапах повторного вычисления значений первого или второго распределения вероятностей подмножества начальных значений первого распределения вероятностей или второго распределения вероятностей соответственно и подмножества множества вероятностей переходов от одной ветви к другой могут использоваться для повторного вычисления соответствующего распределения вероятностей. Далее используются только значения в подмножествах, удовлетворяющие заданному критерию надежности.

В другом варианте осуществления кодер может быть представлен структурой сдвиговых регистров, содержащей по меньшей мере одно из следующего: математические операции прямой связи и математические операции обратной связи.

Кроме того, в другом варианте осуществления данного изобретения код является подходящим для декодирования посредством применения максимального апостериорного алгоритма.

В другом варианте осуществления данного изобретения способ может дополнительно предусматривать этап, на котором используют внутреннюю вероятностную меру для инициализации множества вероятностей переходов от одной ветви к другой.

Другой вариант осуществления данного изобретения охватывает этап, на котором используют внутреннюю вероятностную меру для реконструкции декодированного кодового слова.

В другой вариации этого варианта осуществления декодер, представимый двумя отдельными экземплярами декодера, используют для декодирования по меньшей мере одного кодового слова на первом этапе декодирования и способ может дополнительно предусматривать этап, на котором используют внешнюю вероятностную меру первого экземпляра декодера как внутреннюю вероятностную меру во втором экземпляре декодера.

В другой вариации этого варианта осуществления способ дополнительно предусматривает этап, на котором выполняют вторую итерацию декодирования в первом экземпляре декодера, причем этот экземпляр декодера использует внешнюю вероятностную меру второго экземпляра декодера как внутреннюю вероятностную меру.

Согласно другому варианту осуществления данного изобретения критерий надежности может быть основан по меньшей мере на одном из: на канальных оценках радиоканала, по которому было принято по меньшей мере одно кодовое слово, абсолютных значениях элементов первого и/или второго распределения вероятностей, количестве выполненных этапов декодирования и случайного процесса. В другой вариации критерий надежности может быть не удовлетворен для элемента первого или второго распределения вероятностей, если отношение сигнал-шум для этого элемента и/или абсолютное значение этого элемента находится ниже заданного порогового значения.

Кроме того, данное изобретение обеспечивает в другом варианте осуществления декодер для декодирования по меньшей мере одного кодового слова, причем по меньшей мере одно кодовое слово было генерировано кодером, содержащим структуру, обеспечивающую код, представимый множеством переходов от одной ветви к другой в диаграмме матрицы.

Декодер может содержать средство обработки для инициализации множества вероятностей переходов от одной ветви к другой в декодере на основании принятого кодового слова и структуры кодера, инициализации первого распределения вероятностей и второго распределения вероятностей согласно начальному состоянию кодера, используемого для кодирования по меньшей мере одного кодового слова, повторного вычисления значений первого распределения вероятностей на основе начальных значений первого распределения вероятностей и множества вероятностей переходов от одной ветви к другой с использованием рекурсивного алгоритма, повторного вычисления значений второго распределения вероятностей на основе начальных значений второго распределения вероятностей и множества вероятностей переходов от одной ветви к другой с использованием рекурсивного алгоритма и реконструкции декодированного кодового слова на основе принятого кодового слова и внешней вероятностной меры, вычисленной на основе множества вероятностей переходов от одной ветви к другой, первого и второго распределения вероятностей.

Кроме того, средство обработки может быть выполнено с возможностью использования либо на каждом, либо на обоих этапах повторного вычисления значений первого или второго распределения вероятностей подмножества начальных значений первого распределения вероятностей или второго распределения вероятностей соответственно и подмножества множества вероятностей переходов от одной ветви к другой для повторного вычисления соответствующего распределения вероятностей, причем используются только значения, которые удовлетворяют заданному критерию надежности.

В другом варианте данного изобретения обеспечен декодер, содержащий средства, выполненные с возможностью осуществления вышеупомянутых способов декодирования.

Кроме того, другой вариант осуществления данного изобретения относится к мобильному терминалу в системе мобильной связи, причем мобильный терминал может содержать средство приема для приема по меньшей мере одного кодового слова, средство демодуляции для демодуляции по меньшей мере одного принятого кодового слова и декодер согласно любому из вариантов осуществления данного изобретения.

В другом варианте осуществления мобильный терминал может дополнительно содержать средство кодирования для кодирования данных по меньшей мере в одно кодовое слово и средство передачи для передачи по меньшей мере одного кодового слова, при этом по меньшей мере одно переданное кодовое слово является подходящим для декодирования согласно способам, описанным выше.

В другом варианте осуществления данного изобретения обеспечена базовая станция в системе мобильной связи, причем базовая станция может содержать средство приема для приема по меньшей мере одного кодового слова, средство демодуляции для демодуляции по меньшей мере одного принятого кодового слова и декодер согласно любому из вариантов осуществления данного изобретения.

В другом варианте осуществления базовая станция может дополнительно содержать средство кодирования для кодирования данных по меньшей мере в одно кодовое слово и средство передачи для передачи по меньшей мере одного кодового слова, при этом по меньшей мере одно переданное кодовое слово является подходящим для декодирования согласно способам декодирования, описанным выше.

Кроме того, согласно еще одному варианту осуществления обеспечена система мобильной связи, содержащая по меньшей мере одну базовую станцию согласно любому из вариантов осуществления данного изобретения и по меньшей мере один мобильный терминал согласно любому из вариантов осуществления данного изобретения.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Далее данное изобретение описано более подробно со ссылкой на приложенные чертежи. Подобные или соответствующие подробности в чертежах отмечены одними и теми же ссылочными позициями.

Фиг.1 показывает примерную компоновку кодера сдвиговых регистров для систематического кодирования.

Фиг.2 показывает диаграмму переходов от одного состояния к другому кодера, показанного на фиг.1.

Фиг.3 показывает описание сегмента матрицы для кодера, показанного на фиг.1.

Фиг.4 показывает сегмент матрицы, показывающий переменные для прямой рекурсии.

Фиг.5 показывает сегмент матрицы, показывающий переменные для обратной рекурсии.

Фиг.6 показывает сегмент матрицы, показывающий переменные для решения.

Фиг.7 показывает блок-схему процесса декодирования согласно одному варианту осуществления данного изобретения.

Фиг.8 и 9 показывают блок-схемы процесса декодирования с использованием турбопринципа согласно различным вариантам осуществления данного изобретения.

Фиг.10 показывает блок передатчика и приемника согласно варианту осуществления данного изобретения.

Фиг.11 показывает мобильный терминал согласно варианту осуществления данного изобретения, содержащий передатчик и приемник, показанные на фиг.10.

Фиг.12 показывает базовую станцию согласно варианту осуществления данного изобретения, содержащую передатчик и приемник, показанные на фиг.10.

Фиг.13 показывает архитектурный обзор системы связи согласно варианту осуществления данного изобретения, содержащей мобильный терминал, показанный на фиг.11, и базовую станцию (Узел В), показанную на фиг.12.

ПОДРОБНОЕ ОПИСАНИЕ

В следующих абзацах выражение «х∈А\В» означает «х есть элемент множества А без множества В», что эквивалентно «х есть элемент множества А, но не элемент множества В».

Как описано в предыдущих разделах, математические равенства могут быть решены в инициализации, прямой рекурсии, обратной рекурсии и этапа решения максимального апостериорного алгоритма (см., например, равенства 6, 12, 13, 14 и 15).

Обычно эти равенства содержат следующие члены.

- Равенство для инициализации содержат члены, включающие в себя y величин.

- Равенство для прямой рекурсии содержит члены, включающие в себя Г и определенные величины α.

- Равенство для обратной рекурсии содержит члены, включающие в себя Г и определенные величины β.

Числитель равенства 12 для прямой рекурсии может быть интерпретирован как сумма величин для переходов от одного состояния к другому, которые начинаются в состоянии S_k-1 и заканчиваются в состоянии S_k=m. Следовательно, следующее «прямое множество» может быть определено так:

Т_k,m является множеством состояний S_k-1, где переходы из состояния S_k-1 в S_k возможны посредством информационного бита d_k.

Следовательно,

Подобным же образом числитель равенства 13 для обратной рекурсии может быть интерпретирован как сумма величин для переходов от одного состояния к другому, которые начинаются в состоянии S_k+1 и заканчиваются в состоянии S_k=m. Следовательно, второе «обратное множество» может быть определено так:

U_k,m является множеством состояний S_k+1, где переходы из состояния S_k в S_k+1 возможны посредством информационного бита d_k.

Следовательно,

Согласно данному изобретению множества исключения Δ_k,m и Ω_k,m могут быть дополнительно определены для прямой и обратной рекурсии.

Множество исключения Δ_k,m может указывать те элементы в прямом множестве Т_k,m, которые не выполняют конкретный критерий надежности и, следовательно, не могут использоваться на этапе прямой рекурсии. Подобным же образом множество исключения Ω_k,m может указывать те элементы в обратном множестве U_k,m, которые не выполняют конкретный критерий надежности и, следовательно, не могут использоваться на этапе обратной рекурсии.

С применением множеств исключения Δ_k,m и Ω_k,m равенства могут, следовательно, быть модифицированы следующим образом.

Новая прямая рекурсия

или альтернативно упрощено до

Новая обратная рекурсия

или альтернативно упрощено до

Если оба множества Δ_k,m и Ω_k,m являются пустыми, то дублируется поведение известного уровня техники. Если множество исключения Δ_k,m содержит те же элементы, что и прямое множество Т_k,m, то величина α_k(S_k=m) не может быть определена из формулы рекурсии.

В этом случае может быть полезным установить соответствующее α_k(S_k=m)=-∞. Подобным же образом β_k(S_k=m)=-∞ может быть установлено, когда множество исключения Ω_k,m содержит те же самые элементы, что и обратное множество U_k,m.

В случае если для определенного значения k множество исключения равно прямому множеству для всех m=1...M, α_k(m) может быть установлено на -lnM, что означает, что все состояния S_k=1...M равноподобны. То же самое применимо к обратному множеству.

Обычно множества исключения могут зависеть от индекса m состояния, для которого решается уравнение, от индекса k информационного бита, для которого решается уравнение, и/или от числа итераций процедуры декодирования (например, в контексте турбодекодирования).

Определение множеств исключения Δ_k,m и Ω_k,m

Как описано выше, множества исключения Δ_k,m и Ω_k,m могут быть определены для того, чтобы исключить данные из равенств (или процесса декодирования), которые предполагаются неверными, или которые, очень вероятно, являются неверными. Если такие данные включены, произведенный выход, вероятно, является также неверным. Следовательно, данное изобретение предлагает отбрасывать такие величины из равенств для преодоления их отрицательных вкладов в выход декодирования.

Как отмечалось выше, множества исключения для этапа новой прямой рекурсии (см. равенства 26 или 27) и этапа обратной рекурсии (см. равенство 28 или 29) могут быть определены таким образом, что ненадежные сообщения исключаются из вычислений. В другом варианте осуществления данного изобретения множества исключения могут, например, быть определенными независимо друг от друга, то есть элемент множества исключения Δ_k,m необязательно может быть элементом множества исключения Ω_k,m.

Подобным же образом в другом варианте осуществления данного изобретения множества исключения Δ_k,m и Ω_k,m могут быть установлены независимо в итерациях декодирования. При увеличении числа итераций общая надежность пропускаемых сообщений может быть увеличена для разумно хороших условий передачи. Это может быть, например, применимо к декодированию турбокодов, когда внешняя информация, обмениваемая между объектами декодирования, возрастает по надежности с увеличенным числом итераций декодирования.

Следовательно, при увеличении числа итераций число элементов множеств исключения может быть уменьшено, так что на поздних этапах (в виде итераций) декодирования множества исключения могут быть пустыми.

В другом варианте осуществления данного изобретения множества исключения могут, например, зависеть как от числа итераций, обработанных до сих пор, так и от максимального числа итераций декодирования, которое может быть параметром, данным системой связи. Это может дать возможность постепенного уменьшения элементов во множествах исключения в зависимости от развития шагов итераций.

Примерным списком возможных критериев, которые могут быть использованы изолированно или в комбинации для определения множеств исключения, являются оценка канала (отношение сигнал-шум), абсолютные значения LLR, число итераций (в контексте турбодекодирования) и/или случайный процесс.

Например, критерий оценки канала дает возможность определения множеств исключения согласно воспринимаемому качеству принятых данных. Преимущество может быть в том, что оценка канала обеспечивает сорт независимой дополнительной информации, известной в декодере для оценки надежности принятой кодированной информации. Однако неоднородность оценки канала может быть ограничена сегментом, который состоит из нескольких битов, так что одна эта мера не может быть применима во всех ситуациях для определения множества исключения.

Критерий абсолютного значения LLR может дать возможность оценки надежности с тонкой неоднородностью. Благодаря определению значения LLR, большие абсолютные значения представляют высокую уверенность. Напротив, малое абсолютное значение представляет низкую уверенность. Поэтому ранжирование абсолютных значений LLR может быть использовано для определения самых малых значений для данного равенства, которые должны быть частью множества исключения. Например, критерий значений LLR может быть использован один или в комбинации с другими критериями для определения элементов во множествах исключения.

Другим возможным критерием может быть критерий случайного процесса. Этот критерий может использоваться либо один, либо в соединении с другими критериями для определения членов множества исключения. Например, из-за оценки канала может предполагаться, что 10% принятой информации является ненадежной. Тогда для каждой части информации может существовать шанс в 10% быть членом множества исключения.

Далее, со ссылкой на фиг. 7, 8 и 9, будут описаны различные варианты осуществления данного изобретения.

Фиг.7 показывает блок-схему процесса декодирования согласно одному варианту осуществления данного изобретения. После приема кодового слова y_k через воздушный интерфейс на этапе 701 декодер может генерировать множества исключения Δ_k,m и Ω_k,m на этапе 702.

Для того чтобы генерировать множества исключения, несколько различных параметров решения могут использоваться для решения, какие элементы следует исключить из вычислений на этапах 704, 705 прямой рекурсии и/или обратной рекурсии. Например, приемное средство может обеспечить информацию по качеству канала для приема кодового слова или его индивидуальных битов или даже может обеспечить множества исключения Δ_k,m и Ω_k,m для декодера.

Далее на основе знания структуры кодера и принятого кодового слова y_k вероятности Г(y_k,S_k-1,S_k) переходов от одной ветви к другой могут быть инициализированы на этапе 703. Также распределения α_k и β_k вероятностей инициализируются на этапе 704. Это может быть, например, сделано с использованием знания структуры кодера, используемой для генерации принятого кодового слова y_k.

После соответствующей инициализации декодера, прямая рекурсия и обратная рекурсия, как, например, определено в равенствах 26-29, могут быть выполнены на этапах 705 и 706. В этих рекурсиях рассматриваются множества исключения Δ_k,m и Ω_k,m, то есть только подмножество величин в распределениях α_k, β_k и/или Г(y_k,S_k-1,S_k) может использоваться для выполнения шагов рекурсии.

После повторного вычисления новых величин α_k и β_k кодовое слово может быть реконструировано декодером. Этот этап может, например, включать в себя генерацию внешнего LLR L^e(x^s _k) и критерия оценки L(d_k) для решения на индивидуальных битах декодированного кодового слова d_k.

В другом варианте осуществления может быть далее возможно повторно использовать внешний LLR L^e(x^s _k) или критерий оценки L(d_k) как параметр для инициализации вероятностей Г(y_k,S_k-1,S_k) переходов от одной ветви к другой следующей процедуры декодирования для последующего кодового слова. Однако это может облегчить распространение ошибок декодирования предыдущего кодового слова на следующее кодовое слово.

Фиг. 8 и 9 показывают блок-схемы процесса декодирования с использованием турбопринципа согласно другим примерным вариантам осуществления данного изобретения. В этих примерах множественные экземпляры декодера используются в декодере. Например, такая структура может быть применением для использования турбокодеров/декодеров.

Левая ветвь на фиг. 8 и 9 иллюстрирует работу первого экземпляра декодера, тогда как правая ветвь иллюстрирует работу второго экземпляра декодера. Для лучшей дифференциации между параметрами двух различных экземпляров декодера единицы и двойки были добавлены в верхний индекс или нижний индекс.

По существу, этапы, выполняемые обоими экземплярами декодера, подобны соответствующим этапам, описанным со ссылкой на фиг.7. Поэтому в следующем описании фиг.8 и 9 будем фокусироваться на изменениях, примененных к процессу декодирования.

На фиг.8 приемное средство принимает кодовое слово y_k на этапе 801 и может обеспечить его для первого экземпляра декодера. После генерации или получения множеств исключения Δ¹ _k,m и Ω¹ _k,m (см. этап 702), например, с использованием индикаторов качества приема для индивидуальных битов средства приема вероятности Г¹(y_k,S¹ _k-1,S¹ _k) переходов от одной ветви к другой и величины α¹ _k и β¹ _k могут быть инициализированы (см. этапы 703 и 704). Затем выполняется этап 705 прямой реку