Способ испытаний узлов трения

Способ испытаний узлов трения

Иллюстрации

Показать все

Реферат

Изобретение относится к способам испытаний узлов трения механических систем.

Известен способ определения эксплуатационных условий при испытании узлов трения [1], заключающийся в том, что регистрируют высокочастотные колебания сил контактного взаимодействия в узле трения и проводят гармонический анализ их спектра колебаний, по результатам которого определяют условия эксплуатации узла трения.

Недостатком этого способа является недостаточная достоверность результатов, что обусловлено невозможностью учета влияния динамических процессов, протекающих в механической системе и на фрикционном контакте узла трения, обеспечения идентичности условий протекания процессов трения и изнашивания.

Наиболее близким к описываемому решению является способ определения эксплуатационных условий [2] при испытании узлов трения, заключающийся в том, что испытания проводят на физической модели с необходимым числом сосредоточенных масс, обеспечивая равенство условий трения, логарифмических декрементов затухания и частот колебаний модели и узла, при этом регистрируют высокочастотные колебания сил контактного взаимодействия в узле трения и проводят гармонический анализ их спектра колебаний, по результатам которого определяют условия эксплуатации узла трения.

Недостатком способа прототипа является необходимость применения сосредоточенных масс, размещение которых в необходимых «точках» в некоторых случаях вызывает значительное осложнение, а во многих не представляет возможности, что влечет за собой недостаточную достоверность результатов. Кроме того, измерение параметров микрогеометрии поверхности трения при использовании способа прототипа производится по окончании проведения испытаний, что, в свою очередь, также приводит к снижению достоверности результатов.

Технической задачей заявляемого решения является повышение достоверности результатов определения эксплуатационных условий при испытании узлов трения.

Поставленная задача достигается тем, что в заявляемом способе механические системы объектной и модельной фрикционных механических систем (ФМС), состоят из подсистемы механической и подсистемы (подсистем) фрикционной, при этом механические подсистемы описываются системой аналогичных линеаризованных дифференциальных уравнений, а процессы, протекающие на фрикционном контакте (ФК) «объекта» и «модели», описываются аналогичными математическими моделями, уравнениями регрессии, получаемыми при натурном эксперименте, например, с применением математического планирования полного или дробного факторного эксперимента, при этом между параметрами «объекта» и «модели» обеспечивается следующее соотношение: отношение линейных размеров объекта (L) и модели (l) равно геометрическому масштабу подобия отношение времени протекания исследуемых процессов объекта (T) и модели (t) равно отношение физико-механических параметров материалов (модуля упругости, температуры объемной и ее градиента и т.д.) объекта (Ф) и модели (ф) равно отношение внешних сил, действующих внутри системы, объекта (F) и модели (f) равно отношение площадей объекта (S) и модели (s) равно при этом отношение амплитуд колебаний связей механических подсистем и деформаций микронеровностей объекта (А) и модели (a) равно отношение параметров микрогеометрии фрикционных поверхностей объекта (Н) и модели (h) равно отношение контактного давления объекта (Q) и модели (q) равно отношение линейных скоростей скольжения объекта (V) и модели (ν) равно отношение масс объекта (М) и модели (m) равно отношение жесткостей объекта (С) и модели (с) равно отношение частот колебаний объекта ( Ω) и модели (ω) равно отношение удельных величин спектральных плотностей мощности - спектральная плотность сигнала x(f) в единицу времени Т на частоте Ω, приходящаяся на единицу площади S поверхности), при этом правые части дифференциальных уравнений (внешние возмущающие воздействия математических моделей ФМС) обеспечивают выполнение констант подобия амплитуды колебаний и частоты колебаний при этом измерение трибопараметров ФМС осуществляется во время проведения испытаний, коэффициент трения представляется в виде комплексной функции, т.е. в виде отношения взаимного трибоспектра в тангенциальном и нормальном направлениях к автотрибоспектру в нормальном направлении, действительная часть которого характеризует упругие, а мнимая - диссипативные свойства подсистемы фрикционного контакта, одновременно выполняется контроль и фиксирование удельной площади касания в реальном масштабе времени, например, методом проводимости в паре металл-металл или методом лазерного просвечивания в паре металл-полимер, а значение контактной температуры (максимальной объемной температуры, температуры на вершинах микронеровностей контакта) определяется формулой:

где J - ток, проходящий через контакт,

R_к - сопротивление контакта,

α_Т - коэффициент внешней теплоотдачи,

ρ - удельное сопротивление,

l_к - «длина» контакта.

Рассмотрим предлагаемый способ испытаний узлов трения на примере исследования ФМС «Подвижной состав - верхнее строение пути» с подсистемой фрикционного контакта «колесо - рельс». Для изучения динамических свойств электровоза и верхнего строения пути примем в качестве подвижной единицы электровоз ВЛ80 с конструкционной скоростью движения до 120 км/ч, движущийся по звеньевому стыковому пути, как наиболее сложный вид движения.

Согласно предлагаемому способу испытаний узлов трения моделирование должно состоять из трех этапов.

1. Построение динамической модели механической подсистемы объекта исследования и выявление констант динамического подобия механической подсистемы.

2. Построение динамической модели подсистемы или подсистем фрикционного контакта.

3. Построение модели фрикционно-механической системы.

В первой части моделирования на основе анализа дифференциальных уравнений движения выводятся критерии подобия динамических подсистем. Несмотря на большое разнообразие существующих конструкций машин, динамические качества любой машины могут быть исследованы по общей методике, которая базируется на законах теоретической механики и теории колебаний. Условием динамической эквивалентности исходной и приведенной систем является равенство величин кинетической и потенциальной энергий до и после приведения. Следовательно, система масс расчетной эквивалентной схемы механической системы имеет число степеней свободы, равное выбранному числу масс реального объекта, и движение ее описывается таким же количеством уравнений. Это дает возможность решить задачу моделирования основных динамических характеристик на основе метода анализа дифференциальных уравнений движения расчетной эквивалентной схемы.

Электровоз можно представить как единую механическую систему со многими степенями свободы, состоящую из колесных пар, рам тележек, кузова и связей между этими основными элементами. Источником всех динамических возмущений в пути и подвижном составе является колесная пара, движущаяся по неровностям пути. Конструкция колесной пары и размещенных на ней устройств сильно влияет на ход всех динамических процессов.

Колебания вагонов возникают потому, что колесные пары при своем движении по рельсам и стрелочным переводам совершают сложные пространственные перемещения и тем самым заставляют колебаться на рессорном подвешивании рамы тележек, раму кузова, кузов и сам путь. Таким образом, колебания электровоза начинаются с колесной пары и передаются всем остальным узлам трения электровоза и пути. Прежде всего, рассматриваются вертикальные колебания одной колесной пары.

Дополнительные динамические вертикальные силы, передаваемые колесом электровоза рельсу, вызванные колебаниями надрессорного строения, не должны превышать статическую нагрузку кузова на колесо. Если эти силы достигнут величин, равных статической нагрузке на колесо (235 кН), то при колебаниях надрессорного строения будут возникать такие же силы разгрузки колеса, т.е. возможен сход колеса с рельса.

Силы же, возникающие от инерции необрессоренных масс, могут достигать нескольких сотен кН. Причинами появления сил инерции необрессоренных масс являются неровности на пути и неровности на поверхности катания колес вагонов. Эти неровности делят на изолированные и непрерывные, короткие и длинные. При движении вагона по звеньевому рельсовому пути, соединенному в стыках накладками, всегда возникают соударения колес с рельсами.

В расчетную схему введем следующие допущения [3]. При исследовании движения электровоза как механической системы, взаимодействующей с железнодорожным путем, рамы тележек и кузов, вне зависимости от их конструкции, чаще всего рассматривают как элементы, обладающие лишь определенной массой (m), сосредоточенной в центре тяжести элемента, при этом весьма редко эти элементы рассматриваются как конструкции, имеющие определенным образом распределенные в пространстве массы и жесткости [4]. Кузов, рамы тележек, колесные пары считаем абсолютно жесткими телами. Средние диаметры колес одинаковые. Путь однородно-упругий. Электровоз движется по рельсовому пути с непрерывными вертикальными неровностями η, одинаковыми для обеих рельсовых нитей (η₁=η'₁; η₂=η'₂ и т.д.). Реальные виды рессорного подвешивания, кроме упругих деформаций в вертикальном направлении, могут упруго деформироваться и в горизонтальном направлении, но для упрощения решения задачи расчетные оценки горизонтальных деформаций рессорных комплектов делать не будем. При подпрыгивании кузов, тележки вагона и др. массы совершают перемещения, параллельные плоскости xOz. Жесткость, обусловленную сжатием металла в контакте колеса с рельсом, сжатием диска колеса и самого рельса под колесом (за счет местных его упругих деформаций) представим в виде так называемой «контактной жесткости колеса и рельса».

При таком упрощении не понадобится учитывать колебания в колесе и рельсе, т.е. не будет необходимости использовать дифференциальные уравнения в частных производных, необходимые для описания упругих колебаний соударяющихся тел [3].

Расчетную схему для решения нашей задачи упростим и представим в виде, показанном на фиг.1, рассматривая колебания только одного колеса.

При этом соответствующие массы m_i, жесткости С_i и коэффициенты сопротивления β_i уменьшаются в соответствующее число раз.

На фиг.1 изображена расчетная схема механической системы «подвижной состав - верхнее строение пути». Примем следующие обозначения: m - масса кузова электровоза, m_т - масса обрессоренных частей тележки, m_н - масса необрессоренных частей тележки (колесная пара), m_p - приведенная масса рельса Р65, m_ш - приведенная масса шпалы, m_б - приведенная масса балласта; О, О_т, О_н, О_р, О_ш, О_б - соответствующие центры масс.

На каждую тележку передается половина массы кузова [4]; вертикальные жесткость и коэффициент сопротивления центрального подвешивания на тележку соответственно равны С и β; надбуксового подвешивания для колесной пары - 2С_m и 2β_m; массы обрессоренных и не обрессоренных частей тележки соответственно равны m_т и m_н. Для одного же колеса эти величины будут в 4 раза меньше, т.е.

Внешнее воздействие на механическую систему моделируется неровностью железнодорожного рельса на современном звеньевом пути типовой конструкции согласно формуле, предложенной ВНИИЖТ МПС Н.Н. Кудрявцевым [5]:

где A₀, B₀ - эквивалентные амплитуды неровности железнодорожного пути,

A₀=0,0077 м, B₀=0,0047 м - для хорошего состояния пути;

L_p - длина рельсового звена, L_p=25 м;

Система дифференциальных уравнений вынужденных колебаний электровоза ВЛ80 в вертикальной плоскости с затуханием примет следующий вид:

где k_i - круговые собственные частоты колебаний массы m_i на упругом элементе жесткостью С_i, с; n_i - круговые частоты затухающих колебаний, с^-1.

Так как процессы в оригинале и модели при динамическом подобии должны быть подобны, то они описываются одинаковыми дифференциальными уравнениями.

В первом приближении будем считать, что диссипативные функции незначительно влияют на частоты собственных колебаний, изменяя только логарифмический декремент колебаний, то есть при оценке условий динамического подобия механическую систему будем рассматривать без трения, то есть Ф=0. (В дальнейшем данное допущение устраняется путем введения в модель ФМС модели ФК, чем обеспечивается полное соответствие динамических характеристик объекта и модели ФМС.)

Структура дифференциальных уравнений одинаковая, поэтому рассмотрим только одно из них, например первую строку (1). Запишем дифференциальные уравнения, описывающие движение объекта (о) и модели (м)

где m₀, m_м - массы кузова электровоза объекта и модели; С_о, С_м - коэффициенты жесткости люлечного подвешивания объекта и модели; z_o, z_м - линейные размеры объекта и модели; Ω_o, Ω_м - собственные (вынужденные) частоты колебаний механических систем объекта и модели.

Таким образом, отношения всех характеризующих их величин должны выражаться с помощью масштабов подобия:

где C_m - масштаб подобия массы; С_C - масштаб подобия коэффициентов жесткости; С_г - масштаб подобия геометрических размеров; С _Ω - масштаб подобия частоты колебаний.

Полученные масштабы подобия введем в дифференциальное уравнение (2) для модели, получим следующую зависимость

Условие тождественности дифференциальных уравнений приводит к следующим критериям подобия:

В качестве условия динамического подобия принимаем равенство частот собственных колебаний модели и объекта, то есть C _Ω=1. Тогда получаем из (4) равенство С_m=С_C для поступательного вида движения. При соблюдении указанного условия получаем критерии из чего следует масштаб подобия времени испытаний, равный С_t=1.

Аналогичные условия равенства мы получим, рассматривая трех-, четырех-,..., n - массные системы, то есть принятое условие обеспечивает динамическое подобие модели и объекта механических систем для любой n - массной системы, в т.ч. и для механической системы «подвижной состав - верхнее строение пути».

На основе приведенного выше анализа можно сделать вывод, что для обеспечения динамического подобия моделируемых механических систем необходимо, чтобы при поступательном движении механических систем константы подобия масс и линейной жесткости системы были равны друг другу, т.е. С_m=C_C и при вращательном движении - равенство констант подобия момента инерции и угловой жесткости системы, т.е. С_I=С_C. При этом модельный эксперимент должен проводиться в реальном масштабе времени С_t=1, так как, во-первых, С _Ω=1 и, соответственно, С _Ω=С_t=1; во-вторых, проводя исследования ФМС на физических моделях, мы должны изготавливать модельные пары из тех же материалов, из которых изготовлены реальные поверхности трения. В связи с этим временные интервалы релаксации связей фрикционного контакта в реальных и модельных условиях равны, что обеспечивается равенством С_t=1.

Во второй части анализируется динамическое подобие подсистемы фрикционного контакта узлов трения.

На фрикционном контакте реальных узлов трения механических систем протекают сложные нелинейные процессы, зависящие от большого числа взаимосвязанных факторов, образующих неоднородную систему нелинейных функциональных зависимостей. Вид дифференциальных уравнений движения зависит не только от того, какие материалы используются в узле трения, при каких нагрузках и скоростях они контактируют друг с другом, какое внешнее управляющее воздействие реализуется в системе, но и в какой механической системе функционирует узел трения. Теоретический динамический расчет ФМС - очень трудоемкий процесс, так как состоит из десятков и сотен степеней свободы, с многими допущениями, упрощениями и линеаризацией динамических процессов. В результате этого зачастую получаются результаты расчета, неадекватные реальным условиям эксплуатации. Попытка описать зависимость выходных характеристик ФМС от входных факторов с учетом свойств контактирующих материалов и динамических характеристик механической системы приводит к огромному количеству моделей (до миллиона и более), исследовать которые в конечном счете невозможно вследствие нарушения принципа суперпозиции для нелинейных систем. В результате этого требуется большое количество последующих доводочных испытаний узлов трения реальных машин.

Таким образом, произвести эффективную оптимизацию ФМС теоретически расчетными методами - практически не решаемая задача. Наиболее целесообразным для исследования оптимизации ФМС является применение экспериментально-лабораторных методов, базирующихся на методике физического подобия и моделирования [6...13]. Для решения вопросов комплексных исследований ФМС, для оптимизации их параметров на базе методов физического подобия и моделирования существуют специальные методики и стенды для их реализации, которые обеспечивают реальные условия эксплуатации машин и механизмов с узлами трения.

Корректная физическая модель ФМС доступнее для исследования, чем реальный объект. Более того, некоторые объекты вообще не могут быть изучены непосредственным образом. Если модель достаточно точно отражает поведение системы, то она содержит необходимые ограничения, а это позволяет получить решение, которое отражает возможное для физической реализации состояние системы.

Узел трения «колесо - рельс» является составной частью ФМС «подвижной состав - верхнее строение пути». Массы колеса m₁ и рельса m₂ совершают сложное взаимное перемещение, являются составными частями механической системы (фиг.3). На фиг.3 изображено модельное представление фрикционной механической системы «колесо-рельс»: F_T - сила трения; f - коэффициент трения; F_H - давление; m₁ - масса колеса; m₂ - масса рельса; σ - коэффициент теплоотдачи; λ - теплопроводность; α - температуропроводность; h - высота микронеровности; r - радиус микронеровности; θ - температура контакта; τ - предельное напряжение сдвига.

При этом поверхности взаимного контакта представляют систему низшего уровня, компонентами которого являются микронеровности, которые можно охарактеризовать массой их активного микрообъема и жесткостью заделки.

При фрикционном взаимодействии твердых тел на поверхностях трения происходят сложные механические и физико-химические процессы: окисление, диффузионное перераспределение, фазовые и структурные превращения, упругое и пластическое деформирование микронеровностей, разрушение поверхностных слоев. Чем выше уровень подсистемы, тем менее инерционны эти процессы. Вследствие малости пятен реального контакта каждый контакт существует непродолжительное время. Как указывается в работе /14/, для реальных шероховатых тел при средней скорости относительного перемещения 1 м/с число дискретных контактов в единицу времени оценивается величиной до 100 кГц в зависимости от материалов пар трения, среднего расстояния между микронеровностями и класса чистоты.

В результате взаимного перемещения контактирующих поверхностей взаимодействие компонентов (микронеровностей) на фрикционном контакте возникают вынужденные колебания, что приводит к возникновению вынужденных колебаний с частотой возмущающей силы. Трение скольжения всегда сопровождается возникновением колебаний и выделением тепла /15/. Под активным микрообъемом материала поверхности трения будем понимать ту зону деформаций материалов контактирующих тел, в которой развиваются процессы, приводящие к изменению физико-механических свойств материалов контактирующих поверхностей. То есть активный микрообъем - это тот тонкий трибослой, определяющий в конечном счете триботехнические характеристики пар трения.

При колебаниях активных микрообъемов материала в них самих и в окружающем их слое возникают деформации и соответствующие им напряжения. Частота вынужденных колебаний напряжений для данного активного микрообъема будет определяться числом импульсов взаимодействий микрообъемов в единицу времени. Нормальные и тангенциальные напряжения, возникающие при контакте микронеровностей, будут зависеть от координат, времени, относительной скорости и максимальной объемной температуры, так как, кроме данных колебаний, активные микрообъемы материала испытывают флуктуации вследствие тепловых пиков.

В процессе деформаций активных микрообъемов масс ФК происходит изменение их размеров, разрушение и образование новых. При этом микронеровности контактирующих поверхностей будут формироваться и стремиться занять относительно друг друга такое положение, чтобы потери энергии при взаимном передеформировании микронеровностей были минимально возможны. Поверхности трения приобретают характер равновесной шероховатости и характеризуются относительно стабильными геометрическими очертаниями микронеровностей. Изменение приведенной жесткости механической системы (или приведенного момента инерции) однозначно приводит к реализации переходного процесса трения, по окончании которого на контакте устанавливается новая равновесная шероховатость.

Процесс формирования равновесной шероховатости на поверхностях трения происходит при резонансе между собственной несущей частотой колебаний активных микрообъемов, то есть частотой колебаний напряжений на поверхности контакта, вызванных колебаниями активных микрообъемов, и частотой колебаний напряжений, соответствующих одной из собственных частот колебаний механической системы. Данное устойчивое состояние заключается в формировании одной несущей частоты трибоспектра и совпадении ее с n-й собственной частотой механической системы.

Таким образом, суммарная энергия колебаний механической системы распределена по спектру генерируемых ею частот и представляет по отношению к микронеровностям контактирующих поверхностей внешнее силовое поле колебаний напряжений в тангенциальном и нормальном направлениях. В установившемся режиме работы механической системы параметры данного силового поля постоянны. Спектр частот вынужденных колебаний активных объемов материала фрикционного контакта очень обширен, поэтому практически всегда он «перекрывает» спектр частот возмущающих колебаний, генерируемых механической системой.

Внутреннее трение является одной из физико-механических констант исследуемых материалов и характеризуется безразмерными коэффициентами (коэффициент поглощения, показатель механической добротности, логарифмический декремент колебаний), то есть не зависит от геометрических размеров тел, а значит, и от геометрического масштаба при физическом моделировании.

Величина коэффициента трения зависит от скорости скольжения, так как при этом изменяются условия взаимодействия и разрушения поверхностей. Общепринятая закономерность изменения коэффициента трения от скорости скольжения в виде падающей характеристики существенно меняется при больших скоростях скольжения, так как при этом происходит значительное выделение тепла. Скорость скольжения определяет число взаимодействующих микронеровностей в единицу времени, то есть частота вынужденных колебаний должна быть пропорциональна скорости скольжения. Следовательно, изменение скорости скольжения и, как следствие, частоты вынужденных колебаний приведет к изменению сложившегося равновесного состояния (резонанса) между частотой собственных колебаний активных микрообъемов и частотой вынужденных колебаний. Переход системы в новое устойчивое состояние будет связан с изменением топографии поверхностей трения до установления равновесной шероховатости на другом резонансном уровне. Таким образом, для обеспечения адекватности процессов трения в модели и натуре необходимо обеспечить равенства констант подобия для скорости относительного движения контактирующих поверхностей - С_Vск=1.

Между скоростью скольжения и температурой поверхностного слоя, при прочих равных условиях, существует зависимость: согласно формуле Егера /16/, температура пропорциональна корню из скорости скольжения. При температуре в 100...200°С вследствие дискретного характера контакта доля пластичного контакта в общем напряженно-деформационном состоянии поверхности возрастает и контактное давление уменьшается. Подплавление поверхностей активного микрообъема масс поверхности трения приводит к изменению их формы, что в общем случае сопровождается увеличением фактической площади касания и пропорциональным снижением контактных давлений. Вместе с тем, температура трения от этого не изменяется, т.е. градиент температуры не зависит от давления и вполне определяется скоростью скольжения. Пики температур практически полностью реализуются в активном микрообъеме. Даже при температуре контакта в 800...1000°С объемная температура остального материала будет незначительно отличаться от окружающей 30...60°С /17/. Это позволяет говорить о весьма интенсивном температурном градиенте активного микрообъема. Продолжительность температурного пика и периода перехода от нагревания к охлаждению и наоборот составляет 0,1...1,0 мс /18/. Это позволяет температурные пики характеризовать как параметры, имеющие частоту и амплитуду.

Величина активного микрообъема зависит от физико-механических характеристик контактирующих поверхностей, а также от параметра PV (произведения скорости относительного скольжения на давление) и ограничивается глубиной, на которой влияние температуры на физико-механические свойства материалов трущихся тел материально ощутимо.

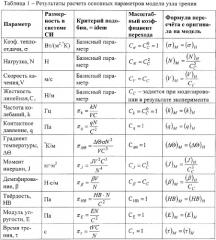
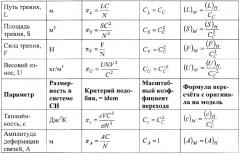
Основным критерием достоверности модельного эксперимента можно считать реализацию в условиях модели одинакового вида изнашивания поверхностных слоев и интенсивность износа контактирующих тел, являющегося основным для реальных поверхностей трения. Проведенный анализ показывает, что для обеспечения условий динамического подобия процессов на поверхности фрикционного контакта при моделировании условий трения необходимо выполнение следующих условий:

- исследователь вправе выбирать геометрический масштаб модели С_г и пропорционально изменять, например, номинальную площадь контакта А, т.е. С_А=С_г ², длину пути трения С_L (C_L=1), радиус кривизны r₁ или r₂ колеса и рельса (С_r=С_г), диаметр круга катания d (С_d=С_г). Однако применять масштабный коэффициент С_г к геометрическим параметрам, определяющим линейные размеры на площади фактического касания (микрошероховатость), нельзя;

- скорости скольжения, т.е. С_Vск=1;

- если режимы контактирования при модельных и натурных испытаниях одинаковы, то параметры шероховатости для установившегося режима трения будут одинаковы, а их константы подобия, например, для высоты микронеровностей С_h, радиуса закругления микронеровностей С_r должны быть равны единице (С_r=1, С_h=1). Это входит в противоречие с принимаемой константой подобия линейных размеров, так как и приведенные параметры единичной микронеровности h и r являются линейными размерами, а С_l≠1. Принудительное изменение шероховатости в соответствии с С_l, как это принято в работе Брауна Э.Д. /19/, при постоянстве параметров контактного давления и скорости скольжения для модели и реального узла трения, то есть С_q=1, С_Vск=1, создает на поверхности неустановившийся режим трения (процесс приработки), который после завершения и выхода на установившийся режим трения приводит к реализации равновесной шероховатости с С_r=1, С_h=1;

- процесс изменения геометрических параметров идет до тех пор, пока на пятнах фактического касания не выравнивается контактное давление q. Это позволяет охарактеризовать контактное давление на поверхности трения как критерий, равенство которого для реальной поверхности трения и модели является определяющим, то есть С учетом полученного из условий динамического подобия условия равенства скоростей скольжения и параметров шероховатости для модели и натуры равенство контактных давлений обеспечивает реализацию на поверхности трения для модельного эксперимента характерного для реальной поверхности вида изнашивания;

- для сохранения равенства контактных давлений на контакте нормальная нагрузка на контакт должна иметь масштабный коэффициент перехода от натуры к модели, равный масштабному коэффициенту площади контакта, то есть С_N=C_S=С_l ²;

- равенство контактных давлений для объекта и модели, т.е. С_q=1, определяет равенство масштабного фактора массы С_m=С_l ², так как, во-первых, контактное давление прямо пропорционально силе и обратно пропорционально площади контакта во-вторых масса прямо пропорциональна силе трения где g - ускорение свободного падения (С_g=1), т.е. масштабный фактор массы имеет размерность силы

- при одинаковых условиях на контакте для модели и реальной поверхности равным сближениям соответствуют равные коэффициенты трения f и равные удельные линейные износы i_h.

- собственные и характерные собственные частоты колебаний (которые следует рассматривать как физико-механическую характеристику поверхности трения при установившемся режиме трения, и в соответствии с формулой для сохранения равенства характерных частот собственный колебаний должно выполняться условие равенства констант подобия жесткости заделки и момента инерции активного микрообъема материала фрикционного контакта относительно ее центра колебаний, то есть C_C=С_I);

- величины амплитуд деформаций контактирующих микро-, макрошероховатостей фрикционного контакта и связей механических систем при модельных и натурных испытаниях равны единице С_A=1, где А - амплитуда колебаний связей и величина шероховатости.

- процесс фрикционного контактирования должен реализовываться в реальном масштабе времени, то есть С_t=1.

На третьем этапе моделирования рассматриваются критерии физического подобия узла трения фрикционно-механической системы.

Узел трения является подсистемой фрикционной механической системы, кроме того, его нельзя рассматривать как подсистему одного уровня. Например, при рассмотрении таких узлов трения, как «втулка - муфта», приведенного на фиг.3, системой является экипаж в пути, подсистемой - ФМС «колесо - смазка - рельс» (структурные составляющие). Подсистемами второго порядка (или элементами подсистем) являются параметры, характеризующие свойства поверхностей трения, трение и износ. В качестве критерия оценки функционирования системы можно принять интенсивность изнашивания поверхностей I.

В конструктивном исполнении рассматриваемой системы можно выделить механизм нагружения, ведущую и ведомые части, связанные жесткостями связей с механической системой привода машины, системой демпфирующих элементов узла трения и т.д. Отмеченные конструктивные элементы узла трения составляют его механическую часть, подуровнем которой непосредственно являются поверхности контакта.

Поэтому при разработке структурной модели сложного процесса (например, торможения локомотива) в работе /20/ модель разбивается на несколько ступеней - группы подсистемы 1-го порядка, каждая из которых делится на подсистемы 2-го порядка и т.д. Соответственно и графическое представление физической модели узла трения (фиг.3). Если в подсистеме механической части узла трения (фиг.3.а) формируются параметры режима (скорость, нагрузка), теплоотдающие поверхности и объемы теплопоглощения, параметры формы (масса, жесткость, моменты инерции, твердость и т.д.), то в подсистеме поверхности трения (фиг.3.б) формируются параметры микрогеометрии контакта (высота и радиус активного микрообъема, величина сближения контактирующих поверхностей), средняя объемная температура фрикционного контакта и температура контакта, напряженно-деформационное состояние активных микрообъемов, амплитудно-фазочастотные характеристики (АФЧХ) процессов внутреннего трения.

Оценка зависимости триботехнических параметров узла трения от параметров нагружения, модификации поверхности трения, температуры, влияния внешней среды позволяет ограничиться подсистемой первого порядка, оценки параметров которой представлены на фиг.3.а и 3.б.

Используя данные модели (фиг.4) процессов трения и изнашивания узла трения «колесо-рельс», представим в общем виде функциональную зависимость процесса:

где σ₁₂ - коэффициент теплоотдачи, Вт/(К·м²); N - нормальная нагрузка колеса на рельс, Н; V - скорость качения, м/с; С - линейная жесткость связей, Н/м; k - частота собственных колебаний, с^-1; q - давление в контакте, Па; ΔΘ - температурный градиент, К/м; J - момент инерции, кг·м²; β - вязкое демпфирование, (Н·с)/м; НВ - твердость материалов, Па; Е - модуль упругости, Па; τ - время трения, с; L - путь трения, м; S - площадь контакта, м²; F - сила трения, Н; U - весовой износ, кг/м³; с - коэффициент удельной теплоемкости, Дж/(кг·К); А - амплитуда деформации связей, м.

На этапе моделирования механического, теплового и динамического подобия всей механической системы необходимо учесть ограничения, определяющие динамику механической системы без трения и условия, ее определяющие, и тождественность аналогичных физических процессов протекания на фрикционном контакте модели и объекта.

Для этого при использовании метода анализа размерностей (с ограничениями /15/) жесткость С как основная варьируемая величина вводится в число базисных параметров, а время τ и контактное давление q - в краевые условия.

В системе основных единиц MLTΘ (масса, длина, время и температура) выбираем четыре базисных параметра, оказывающие наиболее существенное влияние на процессы трения и изнашивания фрикционной с