Способ разделения совмещенных поверхностной и объемной электромагнитных волн терагерцового диапазона

Способ разделения совмещенных поверхностной и объемной электромагнитных волн терагерцового диапазона

Иллюстрации

Показать все

Реферат

Изобретение относится к области передачи и получения информации посредством поверхностных электромагнитных волн (ПЭВ) терагерцового (ТГц) диапазона (частота от 0,1 до 10 ТГц) и может найти применение в спектроскопии поверхности твердого тела, в электронно-оптических устройствах передачи и обработки информации, в инфракрасной (ИК) технике.

С созданием перестраиваемых по частоте (в том числе и в ТГц диапазоне) лазеров на свободных электронах, а также импульсных лазеров, генерирующих фемтосекундные импульсы с шириной спектра до 3000 см^-1, началось интенсивное освоение ТГц области спектра [1]. Одной из важных областей использования ТГц излучения является спектроскопия поверхности твердого тела, а также - передача информации посредством ПЭВ, к классу которых относятся и поверхностные плазмоны на границе "металл-диэлектрик" [2].

В устройствах (спектрометрах, рефрактометрах, датчиках), в которых в качестве носителя информации используют ТГц ПЭВ, сложной проблемой, не нашедшей пока своего эффективного разрешения, является разделение ПЭВ и объемной волны (ОВ), порождаемой падающим излучением на элементе преобразования падающей ОВ в ПЭВ [3].

Известен способ разделения совмещенных поверхностной и объемной электромагнитных волн ТГц диапазона, состоящий в том, что элемент преобразования падающей ОВ в ПЭВ и исследуемую поверхность размещают на смежных гранях образца, разделенных скругленным (для уменьшения радиационных потерь ПЭВ) ребром [4]. Основным недостатком этого способа является наличие за ребром совмещенной с ПЭВ вторичной объемной волны, распространяющейся в плоскости падения и обусловленной дифракцией на ребре первичной объемной волны, порожденной на элементе преобразования.

Известен способ разделения совмещенных поверхностной и объемной электромагнитных волн ТГц диапазона, состоящий в том, что элемент преобразования падающей ОВ в ПЭВ и исследуемую поверхность размещают на одной грани образца, но разделяют их посредством непрозрачного экрана, расположенного перпендикулярно плоскости падения и отделенного от поверхности зазором величиной в (10÷20)·λ, где λ - длина волны падающего излучения [5]. Основным недостатком известного способа является порождение на краю экрана новой объемной волны, распространяющейся в плоскости падения и также пространственно совмещенной с ПЭВ.

Наиболее близким по технической сущности к заявляемому способу является способ разделения совмещенных поверхностной и объемной электромагнитных волн ТГц диапазона, состоящий в том, что на поверхности образца формируют ориентированную своей осью перпендикулярно направлению распространения пучка параллельных лучей ПЭВ и пересекающую его канавку (неоднородность) с цилиндрической поверхностью и сглаженными краями, а над канавкой, на расстоянии не меньше глубины проникновения поля ПЭВ в окружающую среду, размещают непрозрачный экран, ориентированный вдоль оси канавки [6]. Основным недостатком известного способа является порождение на краю экрана (в результате дифракции) новой объемной волны, распространяющейся, как и ПЭВ, в плоскости падения.

Техническим результатом изобретения является полное пространственное разделение ПЭВ и объемной волны (возникшей либо в результате дифракции на элементе преобразования падающего излучения в ПЭВ, либо в результате дифракции ПЭВ на краю экрана, отделяющего элемент преобразования ОВ в ПЭВ и фотоприемник) путем изменения направления ПЭВ.

Технический результат достигается тем, что в способе разделения совмещенных поверхностной и объемной электромагнитных волн терагерцового диапазона, включающем предварительное формирование на поверхности образца канавки со сглаженными краями и осью, перпендикулярной плоскости падения, пересекающей трек пучка лучей поверхностной электромагнитной волны (ПЭВ) и имеющей размер вдоль трека меньше длины распространения ПЭВ, и последующее направление совмещенных волн на канавку, канавку формируют в виде половины правильного конуса, ось которого лежит в плоскости поверхности образца, при этом угол отклонения ПЭВ от плоскости падения, содержащей объемную волну, равен:

γ=arcsin[tg(α)·(π-2)·κ'],

где α - угол между образующей и осью конуса, κ' - действительная часть показателя преломления ПЭВ.

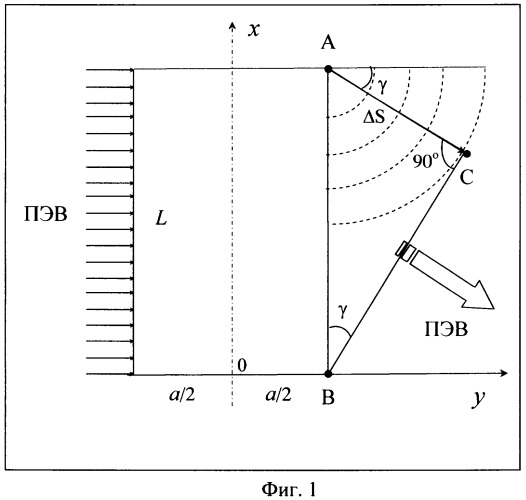
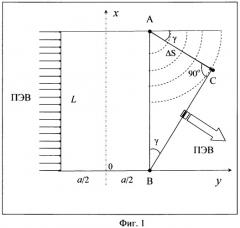
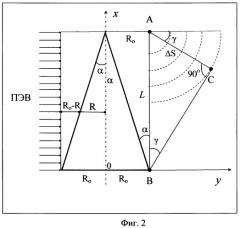
Способ поясняется с помощью трех чертежей. На фиг.1 изображена общая схема неоднородности поверхности образца, обеспечивающей поворот волнового фронта ПЭВ на угол γ, на фиг.2 - схема канавки конической формы в поверхности образца, обеспечивающей поворот ПЭВ на угол γ, на фиг.3 - расчетная зависимость угла γ от угла α между образующей и осью конуса для ПЭВ с λ=100 мкм на поверхности алюминия, граничащей с воздухом.

Эффект разделения совмещенных ПЭВ и ОВ достигается за счет поворота волнового фронта ПЭВ на угол γ в результате преодоления различными лучами пучка ПЭВ созданной неоднородности в различных ее участках.

Приведем обоснование этого утверждения. Пусть ПЭВ, характеризуемая некоторым показателем преломления κ, распространяется по плоской поверхности образца в виде пучка параллельных лучей шириной L, а перпендикулярно направлению распространения ПЭВ на поверхности создана неоднородность в виде "черного" прямоугольника со сторонами L и a, обеспечивающая линейную зависимость оптического пути лучей ПЭВ от координаты луча на оси х, перпендикулярной направлению ПЭВ (фиг.1).

Пусть оптический путь лучей ПЭВ Δl, при прохождении ими неоднородности, определяется линейным выражением: Δl=[(L-х)/L)·а·κ', где κ' - действительная часть комплексного показателя преломления ПЭВ κ.

Тогда разность оптических путей крайних лучей ПЭВ ΔS=Δl(0)-Δl(L)=a·κ'. Следовательно, верхний (по фиг.1) луч ПЭВ достигнет края неоднородности в точке А раньше, чем нижний луч - в точке В на интервал времени Δt=ΔS/ϑ=ΔS/(C/κ')=a·(κ')²/C, где ϑ - фазовая скорость ПЭВ, С - скорость света в вакууме.

Тогда, согласно принципу Гюйгенса - основы волновой теории света, точка А, становится источником вторичных волн с круговым фронтом на время Δt раньше, чем точка В. Но за время Δt вторичные волны, излучаемые точкой А, пройдут расстояние АС=ϑ·Δt=(С/κ')·[a·(κ')²/С]=а·κ'.

И, наконец, из прямоугольного треугольника АВС имеем: sin(γ)=AC/L=a·κ'/L. Откуда, угол отклонения ПЭВ от направления распространения ОВ равен: γ=arcsin(a·κ'/L).

Отметим, что величина угла γ зависит от отношения a/L (размеров неоднородности вдоль и поперек направления распространения совмещенных волн). Поэтому, с точки зрения применимости, заявляемый способ ограничен тем условием, что длина распространения ПЭВ должна превышать продольный (относительно направления распространения волн) размер а неоднородности, иначе ПЭВ просто не дойдет до второго (по ходу излучения) края неоднородности, и проблема разделения волн утратит свою актуальность ввиду исчезновения одного из разделяемых объектов. Это условие легко выполняется для поверхностных плазмонов в ТГц области спектра, поскольку их длина распространения достигает десятков и сотен сантиметров [3-6].

Докажем, что канавка 3, выполненная в виде половины правильного конуса, ось которого лежит в плоскости поверхности образца, обеспечивает линейную зависимость оптического пути лучей ПЭВ от координаты луча на оси, перпендикулярной направлению распространения совмещенных волн (т.е. что такая канавка является, фактически, геодезической призмой [7]), и поэтому может выполнять предписанную ей формулой изобретения функцию.

Пусть ПЭВ с показателем преломления κ распространяется по плоской поверхности образца в виде пучка параллельных лучей шириной L, а перпендикулярно направлению распространения ПЭВ сформирована канавка конической формы, ось которой лежит в плоскости поверхности образца (фиг.2).

Рассчитаем разность геометрических путей ΔS_o крайних лучей пучка ПЭВ, падающего на конусную канавку. Введем следующие обозначения: R_o -радиус "основания" конуса, R - текущий радиус поверхности канавки, L -высота конуса (равная ширине пучка ПЭВ), х - координатная ось, направленная вдоль оси правильного конуса. Выделим на поверхности образца прямоугольник со сторонами 2R_o и L, охватывающий канавку.

Тогда зависимость величины геометрического пути произвольного луча ПЭВ от координаты х имеет вид: S_o(x)=2·(R_o-R)+π·R. Но R(x)=R_o-(R_o/L)-(L-x). Поэтому: S_o(x)=R_o·[(x/L)·(2-π)+π]. Из полученного выражения видно, что величина S зависит от координаты х линейным образом.

Далее, геометрическая разность хода крайних лучей ПЭВ (с координатами х=0 и x=L) равна: ΔS_o=S_o(0)-S_o(L)=R_o·(π-2), а оптическая разность хода этих лучей ΔS=ΔS_o·κ'=R_o·(π-2)·κ' соответственно. Причем время Δt, за которое нижний (на фиг.2) луч ПЭВ пройдет расстояние ΔS, равно: Δt=ΔS/ϑ=[R_o·(π-2)·κ']/(C/κ'), где ϑ - фазовая скорость ПЭВ, С - скорость света в вакууме.

Тогда, согласно принципу Гюйгенса, точка А, до которой верхний луч ПЭВ дошел на время Δt раньше, чем нижний луч до точки В, становится источником вторичных волн с круговым фронтом. За время Δt эти вторичные волны пройдут расстояние AC=ϑ·Δt=(C/κ')·{[R_o·(π-2)·κ']/(C/κ')}=R_o·(π-2)·κ'.

И, наконец, для прямоугольного треугольника АВС имеем: sin(γ)=AC/L=[R_o·(π-2)·κ']/L=tg(α)·(π-2)·κ'. Таким образом, формула для расчета угла отклонения ПЭВ конической канавкой от исходного направления распространения имеет вид: γ=arcsin[tg(α)·(π-2)·κ'].

Отметим, что если ось конуса не лежит в плоскости поверхности образца, то зависимость S(x) не является линейной, и это приводит к различию направлений лучей пучка ПЭВ, прошедшего канавку. В результате волновой фронт пучка ПЭВ искажается, что является неприемлемым в условиях поставленной задачи. Этим фактом объясняется необходимость условия принадлежности оси конуса плоскости поверхности образца.

Условие же нахождения "вершины" конуса на поверхности образца не является обязательным. Действительно, в случае нахождения "вершины" за пределами поверхности (но на ее плоскости) формула для угла γ принимает вид:

где R₁ и R₂ - радиусы поперечного сечения конуса на боковых (относительно трека ПЭВ) гранях образца; L - ширина пучка лучей ПЭВ, равная ширине поверхности образца. Выразив R₁ и R₂ через угол α при "вершине" конуса, мы вновь получим выражение: γ=arcsin[tg(α)·(π-2)·κ'].

Способ осуществляется следующим образом. Пучок лучей монохроматического излучения с ненулевой p-составляющей падает на элемент преобразования и с некоторой эффективностью преобразуется в ТГц ПЭВ, при этом одновременно, в результате дифракции излучения на элементе преобразования, порождается приповерхностная объемная волна (ОВ). Совмещенные в пространстве и имеющие практически одинаковые фазовые скорости пучки лучей ПЭВ и ОВ достигают канавки и здесь их траектории в плоскости падения расходятся: лучи ОВ продолжают распространяться прямолинейно, в то время как лучи ПЭВ устремляются по поверхности канавки, проходя полукруговую траекторию, длина которой прямо пропорциональна расстоянию от "вершины" конуса. В результате, соответствующие лучи пучков ПЭВ и ОВ достигают второго скругленного ребра канавки неодновременно: OB - раньше, ПЭВ - позже. Причем, запаздывание для более близких к "основанию" конуса лучей ПЭВ будет большим, чем для лучей более близких к "вершине" конуса. Различие запаздывания лучей в пучке ПЭВ, в силу принципа Гюйгенса, и приводит к повороту волнового вектора ПЭВ на угол γ.

В качестве примера применения заявляемого способа рассчитаем величину угла γ для ПЭВ, возбужденных излучением с λ=100 мкм на поверхности алюминия, граничащей с воздухом, после прохождения ПЭВ конической канавки с углом α при "вершине" конуса ее поверхности. В этом случае значение длины распространения ПЭВ, полученное с использованием модели Друде для диэлектрической проницаемости алюминия, равно 685 см (что с большим запасом удовлетворяет наложенное выше условие на соотношение длины распространения ПЭВ и радиуса "основания" конической поверхности, который не может быть больше толщины подложки и обычно меньше 10 см).

На фиг.3 приведена расчетная зависимость γ(α). Из графика видно, что для отклонения ПЭВ от плоскости падения, например, на 30° необходимо на поверхности образца изготовить конусную канавку с углом α≈24°40'.

Таким образом, заявляемый способ позволяет осуществить полное пространственное разделение совмещенных поверхностной и объемной электромагнитных волн терагерцового диапазона за счет изменения направления распространения ПЭВ относительно объемной волны.

Источники информации

1. Siegel P.H. Terahertz technology // IEEE Transactions on Microwave Theory and Techniques. - 2002. - v.50. - No.3. - p.910-955.

2. Csurgay A.I., Porod W. Surface plasmon waves in nanoelectronic circuits // Intern. J. of Circuit Theory and Applications. - 2004. - v.32. - p.339-361.

3. Klopfleisch M., Schellenberger U. Experimental determination of the attenuation coefficient of surface electromagnetic waves // Journal of Applied Physics. - 1991. - V.70. - No.2. - p.930-934.

4. Koteles E.S., McNeill W.H. Far infrared surface plasmon propagation // International Journal on Infrared and Millimeter Waves. - 1981. - V.2. - No.2. - p.361-371.

5. Silin V.I., Voronov S.A., Yakovlev V.A., Zhizhin G.N. IR surface plasmon (polariton) phase spectroscopy// Intern. J. Infrared and Millimeter Waves. - 1989. - v.10. - No.1. - p.101-120.

6. Jeon T.-I., Grischkowsky D. THz Zenneck surface wave (THz surface plasmon) propagation on a metal sheet // Applied Physics Letters. - 2006. - v.88. - Article No.061113 (прототип).

7. Ханспенджер Р. Интегральная оптика. Теория и технология // М.: Мир, 1985. - c.321.

Способ разделения совмещенных поверхностной и объемной электромагнитных волн терагерцового диапазона, включающий предварительное формирование на поверхности образца канавки со сглаженными краями и осью, перпендикулярной плоскости падения, пересекающей трек пучка лучей поверхностной электромагнитной волны (ПЭВ) и имеющей размер вдоль трека меньше длины распространения ПЭВ, и последующее направление совмещенных волн на канавку, отличающийся тем, что канавку формируют в виде половины правильного конуса, ось которого лежит в плоскости поверхности образца, при этом угол отклонения ПЭВ от плоскости падения, содержащей объемную волну, равенγ=arcsin[tg(α)·(π-2)·κ'],где α - угол между образующей и осью конуса, k' - действительная часть показателя преломления ПЭВ.