Способ определения фотоэлектрических параметров высокоомных полупроводников
Иллюстрации
Показать всеИзобретение относится к полупроводниковой электронике и может быть использовано в производстве оптоэлектронных и оптических компонентов на этапах проектирования изделий и тестирования заготовок. Техническим результатом изобретения является сокращение времени и упрощение процесса тестирования полупроводниковых материалов. Сущность изобретения: в способе определения фотоэлектрических параметров высокоомных полупроводников, заключающемся в возбуждении нестационарной фотоэдс в объеме кристалла посредством освещения образца интерференционной картиной, сформированной опорным и фазомодулированным сигнальным пучками света, фазовая модуляция сигнального пучка осуществляется непосредственно самим сигналом нестационарной фотоэдс, а фотоэлектрические параметры: время максвелловской релаксации, время релаксации проводимости, их произведение, подвижность носителей заряда и частота волн пространственной перезарядки ловушек, определяются по значению частоты возникающих автоколебаний. 3 ил.
Реферат
Изобретение относится к полупроводниковой электронике и может быть использовано в производстве оптоэлектронных и оптических компонентов на этапах проектирования изделий и тестирования заготовок (кристаллов, подложек, пленок).
Фотоэлектрические параметры, такие как удельная фотопроводимость, подвижность носителей заряда, время максвелловской релаксации и время релаксации фотопроводимости являются одними из важнейших характеристик, описывающих динамику распределения зарядов и полей в полупроводниках [1, 2]. В связи с этим их измерение является необходимым этапом проектирования и тестирования различных оптических и оптоэлектронных приборов (светодиодов, фотодиодов и фоторезисторов, пространственно-временных модуляторов света, голографических запоминающих устройств, голографических интерферометров). Основная трудность таких измерений связана с влиянием объемного заряда на процессы переноса фотоиндуцированных носителей.
Задача определения фотопроводимости и времени ее релаксации может быть решена с помощью известного способа, в котором поверхность полупроводника освещается амплитудно-модулированным пучком света [1]. К образцу прикладывается постоянное напряжение от внешнего источника. Отклик материала регистрируется в виде фототока, возникающего в объеме кристалла. По амплитуде сигнала в области низких частот модуляции и по виду амплитудно-частотной характеристики определяются величина оптически индуцированной электропроводности и время релаксации фотопроводимости. Недостатком способа является то, что величина удельной фотопроводимости не измеряется непосредственно, а рассчитывается с учетом геометрических размеров образца и условий освещения, что вносит дополнительную погрешность.
Определение дрейфовой подвижности носителей заряда может быть осуществлено с помощью способа, основанного на непосредственном измерении времени прохождения носителями заданного расстояния между электродами [1]. В данном способе с помощью двух электродов создается "тянущее" электрическое поле. Два других электрода (зонды) устанавливаются внутри межэлектродного промежутка на некотором расстоянии друг от друга. В процессе измерений на один из зондов подается импульсное напряжение, приводящее к инъекции носителей заряда. Измерение временного промежутка, за который эти носители достигают точки расположения второго зонда, позволяет определить их скорость, а следовательно, и дрейфовую подвижность. Недостатком способа является то, что он позволяет измерить подвижность только неосновных носителей заряда. Измерение подвижности основных носителей заряда осложняется влиянием объемных зарядов. Кроме того, в высокоомных полупроводниках дрейфовая длина носителей может составлять менее 0.1 mm, что затрудняет установку электродов на необходимом расстоянии друг от друга.
Для высокоомных фоторефрактивных полупроводников с монополярной фотопроводимостью существуют способы измерения фотоэлектрических параметров, заключающиеся в измерении скорости релаксации объемных фазовых голограмм [2]. В данных методах непосредственно измеряемой величиной является дифракционная эффективность объемной голограммы, записанной в образце за счет диффузионного или дрейфового механизма. В отсутствие вешнего поля процесс релаксации голограммы происходит по экспоненциальному закону с характерным временем τsc=τM(1+K2LD 2), где К - пространственная частота записанной голограммы, τM - время максвелловской релаксации, LD - диффузионная длина переноса носителей заряда. В присутствии внешнего поля процесс релаксации приобретает осциллирующий характер с частотами колебаний ωscw=(τMKL0)-1, ωdr=KµE0, где L0 - дрейфовая длина носителей заряда в электрическом поле с напряженностью E0. Измерение характерных времен и частот релаксационных процессов позволяет определить удельную фотопроводимость, время максвелловской релаксации и дрейфовую подвижность носителей заряда. Основным недостатком данного способа является то, что его применение ограничено фоторефрактивными полупроводниками, обладающими линейным электрооптическим эффектом. Запись голограмм в материалах, обладающих центром инверсии, невозможна.
Известен способ определения фотоэлектрических параметров примесных некомпенсированных полупроводников [3, 4], основанный на эффекте нестационарной фотоэдс и взятый нами в качестве прототипа. Эффект нестационарной фотоэдс проявляется в виде знакопеременного электрического тока, возникающего в полупроводнике, освещаемом колеблющейся интерференционной картиной, образованной опорным и фазомодулированным сигнальным пучками света. Способ определения фотоэлектрических параметров заключается в измерении частотных зависимостей амплитуды тока Jω. Частотная зависимость нестационарной фотоэдс, возбуждаемой в отсутствие внешних полей, имеет участок линейного роста сигнала, частотно-независимый участок и участок, где сигнал спадает обратно пропорционально частоте фазовой модуляции. Указанные области разделены частотами среза ω1=[τM(1+K2LD 2)]-1 и ω2=(1+K2LD 2)τ-1, по положению которых определяются удельная проводимость, время максвелловской релаксации и время релаксации фотопроводимости τ. На частотной зависимости нестационарной фотоэдс, возбуждаемой в присутствии постоянного внешнего поля, могут присутствовать два резонансных максимума на частотах ωr1=(τMKL0)-1 и ωr2=KµE0, по положению которых определяются частоты собственных колебаний объемного заряда ωscw, ωdr и дрейфовая подвижность µ.
Основными недостатками прототипа являются необходимость использования дорогостоящих приборов регистрации электрических сигналов [спектр-анализаторов, селективных (lock-in) нановольтметров] и необходимость регистрации большого количества экспериментальных данных с последующей математической обработкой, заключающейся в аппроксимации зависимостей и требующей дополнительного времени и вычислительных средств. Как следствие, данные измерения оказываются достаточно трудоемкими и требующими высокой квалификации персонала.
Целью изобретения является сокращение времени и упрощение процесса тестирования полупроводниковых материалов.
Указанная цель достигается возбуждением нестационарной фотоэдс в объеме кристалла посредством освещения образца интерференционной картиной, сформированной опорным и фазомодулированным сигнальным пучками света. Новым является то, что фазовая модуляция сигнального пучка осуществляется непосредственно самим сигналом нестационарной фотоэдс, а фотоэлектрические параметры (время максвелловской релаксации, время релаксации проводимости, их произведение, подвижность носителей заряда и частота волн пространственной перезарядки ловушек) определяются по значению частоты возникающих автоколебаний.
Рассмотрим особенности возбуждения нестационарной фотоэдс в схеме интерферометра с обратной связью. Предположим, что кристалл с монополярной фотопроводимостью (для определенности - электронной) освещается колеблющейся интерференционной картиной, образованной двумя плоскими световыми волнами, одна из которых промодулирована по фазе с частотой ω и амплитудой Δ:
Здесь I0 - средняя интенсивность света, m - контраст интерференционной картины, φ(t) - фаза интерференционной картины. Контраст и амплитуда фазовой модуляции считаются малыми (m, Δ<<1). Такое освещение приводит к появлению переменного электрического тока J с частотой ω в объеме кристалла вследствие эффекта нестационарной фотоэдс. Этот ток вызывает падение напряжения на нагрузочном сопротивлении RL, которое затем усиливается и подается на электрооптический модулятор, где происходит преобразование в фазовую модуляцию светового пучка с амплитудой Δ:
где Jω - комплексная амплитуда тока с частотой ω, Uπ - полуволновое напряжение модулятора, Н - коэффициент передачи усилителя. Таким образом, создается схема интерферометра с замкнутой цепью обратной связи.
Выражение (3) может быть переписано в виде аналогичном известному критерию Баркгаузена, определяющему параметры установившихся колебаний в различных автоколебательных системах:
Далее будем считать усилитель идеальным, т.е. обладающим равномерной амплитудно-частотной характеристикой и неограниченным динамическим диапазоном: H=const(ω, Δ). В этом случае частота и амплитуда колебаний определяются частотной характеристикой и нелинейностью эффекта нестационарной фотоэдс, а не свойствами усилителя и других компонентов измерительной схемы.
При рассмотрении эффекта нестационарной фотоэдс обычно различают два режима возбуждения сигнала: диффузионный (в отсутствие внешнего электрического поля) и дрейфовый (в постоянном электрическом поле).
В диффузионном режиме возбуждения комплексная амплитуда сигнала нестационарной фотоэдс имеет следующий вид [4]:
где S - площадь электродов, σ0 - удельная фотопроводимость, ED - диффузионное поле, Jn(Δ) - функция Бесселя первого рода n-го порядка.
Рассмотрим случай, когда коэффициент передачи усилителя является вещественной величиной: Н=Нr, lm(Hr)=0. Эта ситуация характерна для большинства аналоговых широкополосных усилителей. Из уравнения (4) следует, что в режиме установившихся автоколебаний комплексная амплитуда сигнала нестационарной фотоэдс должна быть вещественной величиной, что, с учетом выражения (5), позволяет определить частоту автоколебаний:
Следует отметить, что эта частота в точности соответствует частоте максимума ωm на амплитудно-частотной характеристике нестационарной фотоэдс. Таким образом, существует возможность измерения параметра ττM, исходя из значения частоты автоколебаний в рассматриваемой схеме интерферометра с обратной связью.
Далее рассмотрим случай, когда коэффициент передачи усилителя является комплексной величиной и принимает следующее значение: H=Hrexp(iπ/4). Эта ситуация соответствует сдвигу сигнала нестационарной фотоэдс на -1/8 периода. Реализация подобного усилителя на аналоговых схемах затруднена, однако может быть решена с использованием цифровых сигнальных процессоров (DSP) и методов цифровой фильтрации сигналов. Из уравнений (4) и (5) находим частоту автоколебаний:
Эта частота соответствует так называемой первой частоте среза ω1 эффекта нестационарной фотоэдс. При малых пространственных частотах (KLD<1) частота генерации равна обратной величине времени максвелловской релаксации
что может быть использовано для определения этого параметра, а также величины удельной проводимости материала: σ0=εε0/τM (ε - диэлектрическая проницаемость, ε0 - электрическая постоянная).
В случае когда широкополосный усилитель задерживает сигнал на +1/8 периода, т.е. H=Hrexp(-iπ/4), частота генерации равна
Эта частота соответствует второй частоте среза ω2 эффекта нестационарной фотоэдс. При малых пространственных частотах (KLD<1) частота генерации равна обратной величине времени релаксации фотопроводимости
что также может быть использовано для диагностики полупроводникового материала.
Перейдем к анализу функционирования схемы интерферометра в дрейфовом режиме возбуждения сигнала. В этом случае к образцу прикладывается постоянное внешнее напряжение, создающее внутри образца поле E0. Комплексная амплитуда сигнала в этом режиме описывается следующим выражением [4]:
Предположим, что к кристаллу приложено достаточно большое напряжение, такое, что выполнены условия E0>>ED, KL0>>1+K2LD 2, а также предположим, что коэффициент передачи широкополосного усилителя - чисто вещественная величина H=Hr. Частота автоколебаний находится из уравнений (4), (11) и равна
Эта частота соответствует одной из частот собственных колебаний объемного заряда в полупроводнике - волн перезарядки ловушек.
В случае когда коэффициент передачи усилителя - чисто мнимая величина H=Hrexp(iπ/2), т.е. когда усилитель кроме усиления сигнала осуществляет также и его сдвиг на -1/4 периода, частота генерации равна
Эта частота соответствует возбуждению второго типа собственных колебаний объемного заряда - дрейфовых волн. Измерив частоту генерации ωg при заданных K и E0, можно легко оценить дрейфовую подвижность носителей заряда µ.
Уравнение (4) определяет также и амплитуду автоколебаний. С учетом выражений (5)-(7), (9), (11)-(13) это уравнение можно представить в следующем виде:
где введено обозначение для нормированного коэффициента передачи , который различен для всех рассмотренных случаев и при необходимости может быть легко рассчитан. Из уравнения (14) следует условие самовозбуждения схемы: .
Таким образом, измерение частоты автоколебаний в диффузионном режиме возбуждения сигнала позволяет определить время максвелловской релаксации τM, время релаксации фотопроводимости τ, их произведение ττM и удельную проводимость σ0, а в дрейфовом режиме - обе частоты собственных колебаний объемного заряда в полупроводнике ωscw, ωdr, а также подвижность носителей заряда µ.
Совокупность существенных признаков изобретения является новой по сравнению с решениями, известными в науке и технике. Авторам впервые удалось показать, что при возбуждении нестационарной фотоэдс в схеме интерферометра с обратной связью возможно возникновение автоколебательного режима, причем амплитуда и частота колебаний определяются нелинейностью эффекта нестационарной фотоэдс и фотоэлектрическими параметрами кристалла, что позволяет использовать разработанную методику для экспресс-диагностики полупроводниковых материалов.
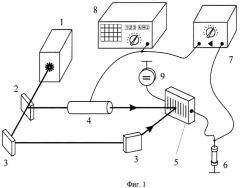
Суть изобретения поясняется Фиг.1-3, где на Фиг.1 представлена схема установки для измерения фотоэлектрических параметров высокоомных полупроводников, где 1 - источник когерентного излучения (лазер), 2 - светоделительная пластина, 3 - зеркала, 4 - фазовый модулятор света, 5 - исследуемый кристалл, 6 - нагрузочное сопротивление, 7 - широкополосный усилитель с регулируемым коэффициентом передачи, 8 - частотомер (осциллограф), 9 - источник высокого напряжения.
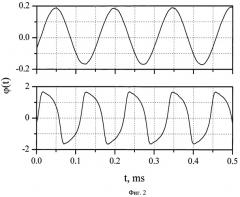
На Фиг.2 представлены осциллограммы колебаний фазы интерференционной картины, генерируемые в схеме интерферометра с обратной связью при диффузионном механизме возбуждения сигнала нестационарной фотоэдс (Е0=0). Показаны зависимости, измеренные при двух значениях коэффициента передачи широкополосного усилителя: H=-6.0×103 (верхний график) и H=-4.5×104 (нижний график).
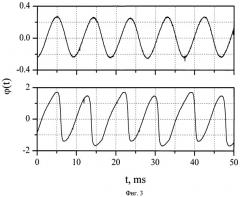
На Фиг.3 представлены осциллограммы колебаний фазы интерференционной картины, генерируемые в схеме интерферометра с обратной связью при дрейфовом механизме возбуждения сигнала нестационарной фотоэдс (E0=10 kV/cm). Показаны зависимости, измеренные при двух значениях коэффициента передачи широкополосного усилителя: H=1.4×104 (верхний график) и H=3.5×104 (нижний график).
Для осуществления способа пучок когерентного света от источника 1 направляется в интерферометр, состоящий из светоделительной пластины 2 и зеркал 3. С помощью фазового модулятора 4 в сигнальном плече интерферометра происходит фазовая модуляция светового пучка, которая далее преобразуется в колебания интерференционной картины в месте пересечения сигнальной и опорной волн. Сформированной интерференционной картиной освещают исследуемый полупроводник 5. Электрический сигнал, возбуждаемый в объеме полупроводника, снимается с нагрузочного сопротивления RL 6, усиливается широкополосным усилителем с регулируемым коэффициентом передачи 7 и подается на фазовый модулятор 4. Частота возникающих автоколебаний измеряется частотомером 8. При необходимости форма колебаний контролируется осциллографом 8. В дрейфовом режиме возбуждения сигнала к кристаллу прикладывается постоянное напряжение от источника 9. Фотоэлектрические параметры материала определяются из измеренных значений частоты генерации в соответствии с выражениями (6), (8), (10), (12), (13).
Экспериментальная проверка предлагаемого способа была выполнена на примере широкозонного полупроводника Bi12SiO20 с электронным типом проводимости [2]. Кристалл имел размеры 10×4×1 mm3. Передняя и задняя поверхности (1×10 mm2) были отполированы до оптического качества, на боковые грани образца были нанесены электроды (3×3 mm2) с помощью пасты на основе мелкодисперсного серебра. Измерения проводились на длине волны второй гармоники Nd:YAG лазера LCM-S-111 (λ=532 mm). Лазер создавал интерференционную картину со средней интенсивностью I0=0.75 W/cm2, контрастом m=0.95, и пространственной частотой K=1.0 µm-1 в экспериментах с диффузионным режимом возбуждения сигнала, и I0=0.10 W/cm2, m=0.17, K=0.16 µm-1 - в экспериментах с дрейфовым режимом. Фазовая модуляция света производилась с помощью электрооптического модулятора МЛ-102А. Использовавшийся широкополосный усилитель обладал следующими характеристиками: коэффициент усиления по напряжению 40-80 dB, фазовый сдвиг 0 и π, равномерность амплитудно-частотной характеристики в диапазоне 1.5 Hz - 150 kHz, максимальная амплитуда выходного напряжения 100 V. Измерения частоты производились с помощью частотомера Ч3-35, форма сигнала контролировалась с помощью аналого-цифрового преобразователя USB3000, подключенного к персональному компьютеру. Сопротивление нагрузки в диффузионном и дрейфовом режимах возбуждения сигнала составляло RL=110 kΩ и 10 kΩ, соответственно. В экспериментах с внешним электрическим полем использовался источник высокого напряжения Б5-24А. С помощью способа-прототипа для исследуемого широкозонного полупроводника были измерены амплитудно- и фазочастотные характеристики нестационарной фотоэдс Jω(ω) в диффузионном и дрейфовом режимах возбуждения. Максимум сигнала на амплитудно-частотных характеристиках достигался на частотах ω/2π=5.9 kHz (E0=0) и ω/2π=120 Hz (E0=10 kV/cm), на этих же частотах фаза сигнала была равна π и 0, соответственно. Из полученных зависимостей были оценены следующие фотоэлектрические параметры материала: ττM=7.3×10-10 s2, ωscw=750 s-1. В предлагаемом способе цепь обратной связи замкнута, и при определенных значениях коэффициента передачи усилителя в рассматриваемой схеме устанавливается автоколебательный режим. Была проведена проверка способа для чисто вещественных значений коэффициента передачи усилителя, т.е. для случаев, когда фазовый сдвиг усилителя равен 0 или π. В отсутствие внешнего электрического поля (диффузионный механизм) автоколебания возникали при отрицательных значениях коэффициента передачи: H<-6.0×103 (Фиг.2). Частота колебаний составила ωg/2π=6.7 kHz, что соответствует следующему значению параметра ττM=5.6×10-10 s2. В случае, когда к кристаллу прикладывается достаточно большое электрическое поле E0=10 kV/cm (дрейфовый механизм), режим генерации колебаний возникает при нулевом фазовом сдвиге усилителя, т.е при положительном значении коэффициента передачи: Н>1.4×104 (Фиг.3). Частота колебаний равна ωg/2π=110 Hz, что соответствует следующему значению частоты волн перезарядки ловушек ωscw=690 s-1. В заключение отметим, что при увеличении коэффициента передачи усилителя наблюдается искажение формы сигнала и изменение частоты генерации (Фиг.2, 3), поэтому для обеспечения большей точности измерений рекомендуется устанавливать значение коэффициента передачи вблизи порога генерации. Из проведенной экспериментальной проверки способа видно, что полученные оценки фотоэлектрических параметров находятся в удовлетворительном согласии с результатами, полученными с помощью способа-прототипа.
По сравнению со способом-прототипом предлагаемый способ обладает существенным преимуществом. Он значительно упрощает и удешевляет схему измерительной установки за счет отказа от дорогостоящих спектр-анализаторов и селективных (lock-in) нановольтметров, а также упрощает и ускоряет процедуру определения параметров однотипных образцов, сводящуюся лишь к измерению частоты генерации вместо измерения и аппроксимации амплитудно-частотных характеристик.
Предлагаемый способ может использоваться не только для измерения фотоэлектрических параметров фоторефрактивных силленитов, использованных в качестве модельного объекта, но и для любых других широкозонных кристаллов, в том числе центросимметричных кристаллов и даже аморфных сред.
Литература
1. С.М.Рыбкин. Фотоэлектрические явления в полупроводниках. - М.: Физматгиз, 1963. - 496 с.
2. М.П.Петров, С.И.Степанов, А.В.Хоменко. Фоторефрактивные кристаллы в когерентной оптике. - С.-Петербург: Наука, 1992. - 320 с.
3. Г.С.Трофимов, С.И.Степанов, М.П.Петров. "Способ преобразования оптического сигнала в электрический", авторское свидетельство №1364039, 1987 (заявка №4015468, приоритет 28.01.1986).
4. I.A.Sokolov, S.I.Stepanov. "Non-steady-state photoelectromotive force in crystals with long photocarrier lifetimes", J. Opt. Soc. Am. В 10, №8, 1483-1488 (1993).
Способ определения фотоэлектрических параметров высокоомных полупроводников, заключающийся в возбуждении нестационарной фотоэдс в объеме кристалла посредством освещения образца интерференционной картиной, сформированной опорным и фазомодулированным сигнальным пучками света, отличающийся тем, что фазовая модуляция сигнального пучка осуществляется непосредственно самим сигналом нестационарной фотоэдс, а фотоэлектрические параметры - время максвелловской релаксации, время релаксации проводимости, их произведение, подвижность носителей заряда и частота волн пространственной перезарядки ловушек - определяются по значению частоты возникающих автоколебаний.