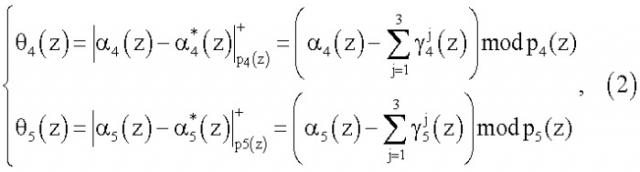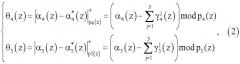Устройство для коррекции ошибок в полиномиальной системе классов вычетов с использованием псевдоортогональных полиномов

Устройство для коррекции ошибок в полиномиальной системе классов вычетов с использованием псевдоортогональных полиномов

Иллюстрации

Показать все

Реферат

Устройство относится к области вычислительной техники, в частности может быть использовано как для контроля и исправления ошибок при передаче информации, так и при проведении арифметических операций в расширенных полях Галуа GF(2^v).

Известно устройство для коррекции ошибок в полиномиальной системе классов вычетов (ПСКВ) с использованием псевдоортогональных полиномов (патент №2294529, G01F 11/08, G06N 3/02, бюл. №6 от 27.02.2007), содержащее вход устройства, регистр, блок вычисления синдрома ошибки, представляющего собой двухслойную нейронную сеть, сумматор и выход устройства.

Недостатком данного устройства являются значительные схемные затраты.

Техническим результатом, достигнутым при осуществлении заявленного изобретения, является снижение схемных затрат.

Указанный технический результат достигается за счет исключения блока памяти, предназначенного для хранения констант коррекции результата и включения в состав блока вычисления синдрома ошибки, представляющего собой двухслойную нейронную сеть, дополнительного третьего слоя нейронов.

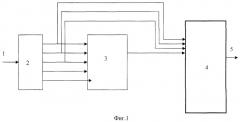
Структура устройства представлена на фиг.1. Устройство состоит из регистра 2, предназначенного для хранения остатков по рабочим и контрольным основаниям ПСКВ в течение времени обнаружения ошибки, вход которого соединен со входом 1 устройства, блока вычисления синдрома ошибки 3, входы которого соединены с выходами регистра 2, сумматора 4, осуществляющего исправления ошибки путем суммирования комбинаций кода ПСКВ с корректирующим значением, Δ_кор, представленным в ПСКВ по рабочим основаниям, первый, второй и третий входы которого соединены соответственно с тремя первыми выходами регистра 2, по которым передаются остатки рабочих оснований, а четвертый вход соединен с выходом блока вычисления синдрома ошибки 3, по которому передается константа ошибки Δ_кор, выход сумматора 4 является выходом 5 устройства.

Работа устройства для коррекции ошибок в полиномиальной системе классов вычетов с использованием псевдоортогональных полиномов осуществляется следующим образом.

На вход 1 устройства для коррекции ошибок в ПСКВ подается контролируемое число, представленное в модулярной форме

и где α_i(z)=A(z)modp_i(z), i=1÷5, p₁(z), p₂(z), р₃(z) - рабочие основания ПСКВ, p₄(z), p₅(z) - контрольные основания системы ПСКВ.

Данный код записывается в регистре 2. Затем с выхода регистра 2 код ПСКВ в двоичном виде поступает на вход блока вычисления синдрома ошибки 3, который представляет собой трехслойную нейронную сеть. Модулярный код ПСКВ A(z)=(α₁(z),α₂(z),α₃(z),α₄(z),α₅(z)) записывается нейронами первого слоя блока 3. С выходов нейронов первого слоя сигналы в двоичном виде поступают на второй слой нейронной сети, который осуществляет вычисление синдрома ошибки согласно выражениям

где - ортогональные базисы безызбыточной системы ПСКВ, определяемые рабочими основаниями p_j(z), j=1, 2, 3.

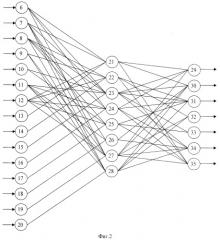
С выходов нейронов второго слоя значения синдрома ошибки θ₄(z) и θ₅(z) в двоичном коде поступают на входы нейронов третьего слоя. Данные нейроны осуществляет вычисление константы ошибки Δ_кор, представленной в виде кода ПСКВ по рабочим основаниям p₁(z), p₂(z), р₃(z). Полученные значения поступают на четвертый вход сумматора 4, где суммируются с полиномом A(z)=α₁(z), α₂(z), α₃(z), представленным по рабочим основаниям ПСКВ, и поступившим с выходов регистра 2 на первые три входа сумматора 4. Исправленное значение A(z) с выхода сумматора 4 попадает на выход 5 устройства. Блок вычисления синдрома ошибки представлен на фиг.2. Он имеет 5 входов, по первым трем из которых подаются остатки α₁(z), α₂(z), α₃(z) по рабочим основаниям p₁(z), p₂(z), р₃(z), по четвертому и пятому поступает остатками α₄(z) и α₅(z) по контрольным основаниям p₄(z) и p₅(z). Блок вычисления синдрома ошибки представляет собой трехслойную нейронную сеть. Первый слой содержит 15 нейронов, второй слой 8 нейронов, а третий слой - 7 нейронов. Входы нейронов 6, 7-8, 9-12 подключены соответственно к первому, второму и третьему входам блока вычисления синдрома ошибки. Входы нейронов 13-16 и 17-20 подключены соответственно к четвертому и пятому входам блока вычисления синдрома ошибки. На данные входы 6, 7-8, 9-12, 13-16 и 17-20 нейронов поступают остатки α₁(z), α₂(z), α₃(z), α₄(z), α₅(z), соответственно представленные в виде двоичных кодов. Старшие разряды остатков α₁(z), α₂(z), α₃(z), α₄(z), α₅(z) записываются соответственно в нейроны 6, 7, 9, 13, 17 первого слоя. Второй слой нейронной сети содержит 8 нейронов, выполняющих базовую операцию (2), причем первые четыре нейрона 21-24 определяют значение θ₄(z), остальные нейроны 25-28 определяют значение θ₅(z). Входы нейрона 21 второго слоя соединены с выходами нейронов 6, 7, 12, 13 первого слоя. Входы нейрона 22 второго слоя соединены с выходами нейронов 8, 9, 12, 14 первого слоя. Входы нейрона 23 второго слоя соединены с выходами 6, 7, 8, 10, 11, 15 нейронов первого слоя. Входы нейрона 24 второго слоя соединены с выходами 6, 8, 11, 12, 16 нейронов первого слоя. Входы нейрона 25 второго слоя соединены с выходами 8, 10, 12, 17 нейронов первого слоя. Входы нейрона 26 второго слоя соединены с выходами 7, 11, 18 нейронов первого слоя. Входы нейрона 27 второго слоя соединены с выходами 6, 7, 9, 11, 12, 19 нейронов первого слоя. Входы нейрона 28 второго слоя соединены с выходами нейронов 7, 8, 9, 11, 20 первого слоя. Старшие значения синдрома ошибки θ₄(z) и θ₅(z) соответственно вычисляются в нейронах 21 и 25. Выходы нейронов второго слоя подключены ко входам нейронов третьего слоя. Третий слой блока вычисления синдрома ошибки содержит 7 нейронов 29-35, с выхода нейрона 29 снимается корректирующее значение константы ошибки Δα₁(z) по первому рабочему основанию p₁(z). С выходов нейронов 30-31 снимается корректирующее значение константы ошибки Δα₂(z) по второму рабочему основанию p₂(z). С выходов нейронов 32-35 снимается корректирующее значение константы ошибки Δα₃(z) по третьему рабочему основанию р₃(z). Корректирующие значения Δα_j(z), j=1, 2, 3 представляются в двоичном коде, причем старший разряд Δα₁(z) вычисляется в нейроне 29, старший разряд Δα₂(z) - в нейроне 30, старший разряд Δα₃(z) - в нейроне 32. Входы нейрона 29 третьего слоя соединены с выходами нейронов 21, 23, 26, 27 второго слоя. Входы нейрона 30 третьего слоя соединены с выходами нейронов 21, 23, 26, 27, 28 второго слоя. Входы нейрона 31 третьего слоя связаны с выходами нейронов 22, 23, 24, 25, 28 второго слоя. Входы нейрона 32 третьего слоя связаны с выходами нейронов 22, 27, 28 второго слоя. Входы нейрона 33 третьего слоя связаны с выходами нейронов 23, 25 второго слоя. Входы нейрона 34 третьего слоя соединены с выходами нейронов 23, 24, 26, 27, 28 второго слоя. Входы нейрона 35 третьего слоя соединены с выходами нейронов 21, 22, 24, 25, 27 второго слоя. Выходы нейронов третьего слоя являются выходом блока вычисления синдрома ошибки.

Рассмотрим работу устройства. В качестве рабочих оснований выбраны p₁(z)=z+1, p₂(z)=z²+z+1, p₃(z)=z⁴+z³+z²+z+1.

Данные основания образуют рабочий диапазон

В качестве контрольных оснований выбраны минимальные многочлены расширенного поля Галуа GF(2⁴)

p⁴(z)=z⁴+z³+1 и p₅(z)=z⁴+z+1.

Если полином A(z), представленный в ПСКВ, не содержит ошибки, то его степень не должна превышать степень рабочего диапазона, т.е.

В противном случае полином содержит ошибку.

Пусть на вход устройства подается полином, принадлежащий рабочему диапазону A(z)=z⁵+z⁴+z+1, значение которого в модулярном коде ПСКВ имеет вид

A(z)=(0, z, z³+z²+1, 1, z²+z).

Тогда данный полином можно представить в виде суммы псевдоортогональных полиномов

Псевдоортогональные полиномы ПСКВ получаются из ортогональных базисов безызбыточной системы ПСКВ (задается рабочими основаниями p₁(z), р₂(z), р₃(z)), которые расширены по контрольным основаниям p₄(z) и р₅(z). В таблице 1 представлены псевдоортогональные полиномы ПСКВ поля GF(2⁴).

Для данного полинома имеем следующие псевдоортогональные полиномы

A₁(z)=(0,0,0,0,0);

A₂(z)=(0,z,0,z³+z,z²+z+1);

A₃(z)=(0,0,z³+z²+1,z³+z+1,1);

Тогда согласно выражению

Таблица 1
Псевдоортогональные полиномы ПСКВ поля GF(24)
Основание ПСКВ	Псевдоортогональный полином
p1(z)=z+1	(1,0,0,z3+z+1,z)
p2(z)=z2+z+1	(0,1,0,z2+1,z3+1)
(0,z,0,z3+z,z2+z+1)
(0,z+1,0,z3+z2+1,z3+z2+z)
p3(z)=z4+z3+z2+z+1	(0,0,1,z3+z2+1,z3+z)
(0,0,z,z+1,z2+z+1)
(0,0,z+1,z3+z2+z,z3+z2+1)
(0,0,z2,z,z3)
(0,0,z2+1,z3+z2+z+1,z)
(0,0,z2+z,1,z3+z2+z+1)
(0,0,z2+z+1,z3+z2,z2+1)
(0,0,z3z2,z+1)
(0,0,z3+1,z3+1,z3+1)
(0,0,z3+z,z2+z+1,z2)
(0,0,z3+z+1,z3+z,z3+z2+z)
(0,0,z3+z2,z2+z,z3+z+1)
(0,0,z3+z2+1,z3+z+1,1)
(0,0,z3+z2+z,z2+1,z3+z2)
(0,0,z3+z2+z+1,z3,z2+z)

имеем

α₄ ^*(z)=0+(z³+z)+(z³+z+1)=1

α₅ ^*(z)=0+(z²+z+1)+1=z²+z

Согласно выражению (2) определяем значения

Данный результат был получен на выходе второго слоя нейронов блока вычисления синдрома ошибки 3. Тогда на выходе нейронов третьего слоя получаем корректирующее значение константы ошибки Δ_кор=(0,0,0), которое подается на четвертый вход сумматора 4 с образованием на выходе A(z)=(0,z,z³+z²+1)+(0,0,0)=(0,z,z³+z²+1).

Допустим, что ошибка произошла в первом основании. Тогда имеет

А_ош(z)=(1,z,z³+z²+1,1,z²+z).

Псевдоортогональные полиномы имеют вид

A₁(z)=(1,0,0,z³+z²+1,z)

A₂(z)=(0,z,0,z³+z,z²+z+1)

A₃(z)=(0,0,z³+z²+1,z³+z+1,1);

Тогда согласно выражению (5)

α₄ ^*(z)=((z³+z+1)+(z³+z)+(z³+z+1))modp₄(z)=z³+z

α₅ ^*(z)=((z)+(z²+z+1)+1)modp₅(z)=z².

На основании (2) получаем синдром ошибки

Таблица 2
Значения Δкор для различных значений вектора ошибки
Вектор ошибки	Значение Δкор
θ4(z)	θ5(z)
0	0	(0,0,0)
z3+z+1	z	(1,0,0)
z3+z	z2+z+1	(0,z,0)
z2+z+1	z3+1	(0,1,0)
z2	z+1	(0,0,z3)
z	z3	(0,0,z2)
z+1	z2+z+1	(0,0,z)
z3+z2+1	z3+z	(0,0,1)

Так как синдром ошибки отличен от нуля, то это свидетельствует о том, что полином содержит ошибку.

Согласно таблице 2 константа ошибки Δ_кор=(1,0,0), данное значение подается на сумматор 4, с выхода которого получаем A(z)=А_ош(z)+Δ_кор(z)=(1,z,z³+z²+1)+(1,0,0)=(0,z,z³+z²+1). Ошибка исправлена.

Рассмотрим работу блока вычисления синдрома ошибки. На вход подан модулярный код А_ош(z)=(1,z,z³+z²+1,1,z²+z). Данный код поступает на входы нейронов первого слоя в двоичном коде согласно таблице 3.

Таблица 3
Сигналы на входах нейронов первого слоя
Нейрон	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Сигнал	1	1	0	1	1	0	1	0	0	0	1	0	1	1	0

Данные нейроны в вычислении синдрома ошибки не участвуют, а предназначены для перераспределения входных сигналов на входы нейронов второго слоя, которые реализуют базовую операцию суммирования по модулю два. В таблице 4 представлены значения сигналов на входе и выходе нейронов второго слоя. Символ

«-» соответствует отсутствию связи между нейронами первого и второго слоя.

Таблица 4
Сигналы на выходе нейронов второго слоя
нейроны	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	выход
21	1	1	-	-	-	-	1	0	-	-	-	-	-	-	-	1
22	-	-	0	1	-	-	1	-	0	-	-	-	-	-	-	0
23	1	1	0	-	1	0	-	-	-	0	-	-	-	-	-	1
24	1	-	0	-	-	0	1	-	-	-	1	-	-	-	-	1
25	-	-	0	-	1	-	1	-	-	-	-	0	-	-	-	0
26	-	1	-	-	-	0	-	-	-	-	-	-	1	-	-	0
27	1	1	-	1	-	0	1	-	-	-	-	-	-	1	-	1
28	-	1	0	1	-	0	-	-	-	-	-	-	-	-	0	0

Таким образом, на выходе второго слоя определен синдром ошибки θ₄(z)=z³+z+1 и θ₅(z)=z, представленный двоичным кодом.

Данный код поступает на входы нейронов третьего слоя, которые реализуют операцию логического умножения И. В таблице 5 представлены значения на входе и выходе нейронов третьего слоя.

Таблица 5
Сигналы на выходе нейронов третьего слоя
Нейроны	21	22	23	24	25	26	27	28	выход
29	1	-	1	1	-	-	1	-	1
30	1	-	1	-	-	0	1	0	0
31	-	0	1	1	0	-	-	0	0
32	-	0	-	-	-	-	1	0	0
33	-	-	1	1	-	0	1	0	0
34	-	-	1	1	-	0	1	0	0
35	1	0	-	1	0	-	1	-	0

Таким образом, на выходе блока вычисления синдрома ошибки определено значение константы ошибки Δ_кор=(1,0,0), которое поступает на вход сумматора, где и происходит коррекция модулярного кода ПСКВ.

1. Устройство для коррекции ошибок в полиномиальной системе классов вычетов с использованием псевдоортогональных полиномов содержит вход устройства, регистр, блок вычисления синдрома ошибки, предназначенный для вычисления констант ошибки, сумматор, выход которого является выходом устройства, причем вход регистра подключен ко входу устройства, а его пять выходов подключены к соответствующим входам блока вычисления синдрома ошибки, кроме того, первый, второй и третий выходы регистра подключены к соответствующим входам сумматора, выход блока вычисления синдрома ошибки подключен к четвертому входу сумматора, при этом на четвертый вход сумматора подаются вычисленные константы ошибок, а блок вычисления синдрома ошибки выполнен в виде трехслойной нейронной сети.

2. Устройство по п.1, отличающееся тем, что блок вычисления синдрома ошибки представляет собой трехслойную нейронную сеть, первый слой которой содержит пятнадцать нейронов, второй - восемь нейронов, третий - семь нейронов, при этом первый слой предназначен для записи контролируемого числа, представленного в полиномиальной системе классов вычетов, второй слой предназначен для вычисления синдрома ошибки, а третий слой - для вычисления констант ошибки, представленных в полиномиальной системе классов вычетов по рабочим основаниям, причем входы нейронов первого слоя являются входом блока вычисления синдрома ошибки, а выходы нейронов третьего слоя являются выходом блока вычисления синдрома ошибки, при этом на входы нейронов с первого по седьмой упомянутого первого слоя поступают остатки по рабочим основаниям контролируемого числа, на входы нейронов с восьмого по пятнадцатый упомянутого первого слоя поступают остатки по контрольным основаниям контролируемого числа, входы первого нейрона упомянутого второго слоя соединены с выходами первого, второго, седьмого и восьмого нейронов упомянутого первого слоя, входы второго нейрона упомянутого второго слоя соединены с выходами третьего, четвертого, седьмого и девятого нейронов упомянутого первого слоя, входы третьего нейрона упомянутого второго слоя соединены с выходами первого, второго, третьего, пятого, шестого и десятого нейронов упомянутого первого слоя, входы четвертого нейрона упомянутого второго слоя соединены с выходами первого, третьего, шестого, седьмого и одиннадцатого нейронов упомянутого первого слоя, входы пятого нейрона упомянутого второго слоя соединены с выходами третьего, пятого, седьмого и двенадцатого нейронов упомянутого первого слоя, входы шестого нейрона упомянутого второго слоя соединены с выходами второго, шестого и тринадцатого нейронов упомянутого первого слоя, входы седьмого нейрона упомянутого второго слоя соединены с выходами первого, второго, четвертого, шестого, седьмого и четырнадцатого нейронов упомянутого первого слоя, входы восьмого нейрона упомянутого второго слоя соединены с выходами второго, третьего, четвертого, шестого и пятнадцатого нейронов упомянутого первого слоя, при этом входы первого нейрона упомянутого третьего слоя соединены с выходом первого, третьего, четвертого и седьмого нейронов упомянутого второго слоя, входы второго нейрона упомянутого третьего слоя соединены с выходами первого, третьего, шестого, седьмого и восьмого нейронов упомянутого второго слоя, входы третьего нейрона упомянутого третьего слоя соединены с выходами второго, третьего, четвертого, пятого и восьмого нейронов упомянутого второго слоя, входы четвертого нейрона упомянутого третьего слоя соединены с выходами второго, седьмого и восьмого нейронов упомянутого второго слоя, входы пятого нейрона упомянутого третьего слоя соединены с выходами третьего и пятого нейронов упомянутого второго слоя, входы шестого нейрона упомянутого третьего слоя соединены с выходами третьего, четвертого, шестого, седьмого и восьмого нейронов упомянутого второго слоя, входы седьмого нейрона упомянутого третьего слоя соединены с выходами первого, второго, четвертого, пятого и седьмого нейронов упомянутого второго слоя.