Нейронная сеть основного деления модулярных чисел

Нейронная сеть основного деления модулярных чисел

Иллюстрации

Показать все

Реферат

Изобретение относится к вычислительным модулярным нейрокомпьютерным системам и предназначено для выполнения основной операции деления модулярных чисел, когда делимое и делитель являются произвольными числами.

Известна нейронная сеть для округления и масштабирования чисел, представленных в системе остаточных классов (патент RU 2271570, G06 3/04, опубликованная 10.03.2006, Бюл. №7), содержащая входной слой нейронов, нейронную сеть конечного кольца определения ранга числа, нейронную сеть конечного кольца вычисления остатка по основанию n+1, нейронную сеть конечного кольца вычисления разности между входными остатками и остатками по основанию n+1, n - нейронные сети конечного кольца вычисления масштабированного числа.

Недостатком данной нейронной сети является невозможность вычисления операции основного модулярного деления чисел.

Наиболее близким к данному изобретению техническим решением является устройство, представленное в виде "Нейронной сети для деления чисел, представленных в системе остаточных классов" (Патент RU 2305312 G06 7/52, G06N 3/02, опубликовано 27.08.2008, Бюл.№24).

Недостатком устройства является большой объем оборудования.

Однако такие нейронные сети предназначены для деления модулярных чисел в случаях, когда в качестве делителя используется целое положительное число, попарно простое с p₁, р₂, …, p_n, либо целое положительное число, представляющее собой произведение чисел, попарно простых с p₁, p₂, …, p₃.

Целью данного изобретения является расширение функциональных возможностей известной нейронной сети для выполнения операций модулярного деления чисел в случаях, когда делимое и делитель являются произвольными числами, и сокращение объема оборудования.

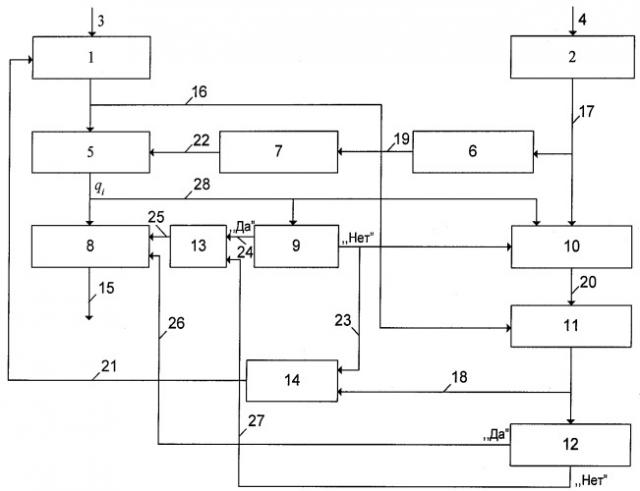
Поставленная цель достигается тем, что нейронная сеть основного деления модулярных чисел содержит: входные регистры для приема и хранения делимого 1 и делителя 2, на входы которых поступают, соответственно, делимое 3 и делитель 4; нейронную сеть для деления чисел 5, представленных в системе остаточных классов (патент RU 3218239, опубликовано 27.02.2008, Бюл. №6); нейронную сеть для преобразования остаточного кода в двоичный позиционный код 6 (патент RU 3218238, опубликовано 27.02.2008, Бюл. №6), в этом изобретении используются только коэффициенты a_i, представленные в ОПСС; постоянное запоминающее устройство 7 для хранения цифр приблизительного делителя; сумматор 8 для формирования частного, полученного от деления; блок сравнения промежуточных частных q_i с нулем 9; блоки умножения делителя на промежуточные значения частных q_i 10; блоки вычитания произведений делителя b и промежуточного частного q_i из значения исходного делимого a или промежуточных значений a_i 11; блок сравнения промежуточного делимого a_i с величиной b/2 12; ключ 13 для считывания частного и блок запрета 14 для записи в регистр делимого нового промежуточного значения a_i 14 и шину 15 для значений частного; информационные шины 16-21, 28 для обмена данными между устройствами и схемами нейронной сети основного деления модулярных чисел и шин управления 22-27.

Известные изобретения связаны со специальными случаями и неприменимы в ситуации, когда и делимое, и делитель представляют собой произвольные целые числа.

Различные алгоритмы деления целых чисел можно описать итеративной схемой, используемой так называемый метод спуска Ферма. Конструируется некоторое правило φ, которое каждой паре целых положительных чисел a и b ставит в соответствие некоторое целое положительное q такое, что a-bq=r>0. Тогда деление a на b осуществляется по следующему правилу: согласно операции φ паре чисел a и b ставится в соответствие число q₁, такое, что a-bq₁=r₁≥0. Если r₁<b, то деление закончено, если же r₁≥b, то, согласно φ, паре чисел (r₁,b) ставится в соответствие q₂, такое, что r₁-bq₂=r₂≥0.

Если (r₂<b), то деление завершается, если же (r₂≥b), то, согласно φ₁, паре (r₂,b) ставится в соответствие q₃ такое, что r₂-bq₃=r₃≥0 и так далее. Так как последовательное применение операции φ приводит к строго убывающей последовательности положительных чисел α≥r₁>r₂>r₃…≥0, то процесс является конечным и алгоритм реализуется за конечное число шагов.

В общем случае b может быть и не равным модулю или их произведению. Здесь встает проблема выбора b таким образом, чтобы оно было равным либо модулю, либо их произведению. Если эта проблема будет решена, тогда итерации могут быть сведены к процессу масштабирования, который рассмотрен выше. Для решения этой проблемы вначале рассмотрим без доказательства теорему о границах изменения b.

Теорема. Если на K-ом шаге зафиксирован случай 0≤r_k-1-bq_k=r_k<b, тогда частное q от деления целых чисел a на b будет равно . Если

Проблема разработки оптимальных вычислительных алгоритмов деления побуждает к разработке таких операций φ₁, которые бы минимизировали число шагов спуска Ферма и вместе с тем достаточно просто реализовывались на заданной вычислительной базе. Кроме того, на способ формирования операций φ существенно влияет также принятая система кодирования числовой информации.

Метод, который будет описан ниже, направлен на использование деления на приблизительный делитель . Этот приблизительный делитель будет выбран из значений делителя, допускаемых в применении алгоритма масштабирования. Так как, в основном случае, b не равно , ошибка представлена в частном, которое при выполнении итерации будет уменьшаться до нуля.

Значение для найдем из соотношения b≤<2b, где - это допустимый делитель для алгоритма масштабирования.

В алгоритме деления первым этапом является этап вычисления частного по алгоритму масштабирования, при котором .

Найденный таким образом q₁ используется в рекурсивных соотношениях для получения q₂, q₃ и так далее.

Эта повторяющаяся процедура продолжается пока q_i≠0. Если это возникает на r-ом шаге повторения, то

где

Действительность этого алгоритма зависит от трех предпосылок:

1. Или q_i, или α_i становятся нулевыми после последнего числа повторений.

2. Ряд должен быть равным .

3. Для любого b существует подходящий и этот можно найти. Подходящий определен как удовлетворяющий условию b≤<2b и также удовлетворяющий условию алгоритма масштабирования.

Приблизительный делитель можно найти путем использования наиболее значимой ненулевой цифры, представлен в полиадической системе счисления. Эту ненулевую цифру заменим ближайшим простым числом или произведением простых чисел. Тогда делитель можно представить в виде простого числа или произведения простых чисел, что позволит использовать для вычисления частного алгоритм масштабирования.

Для определения можно составить таблицу приблизительного делителя. В таблице приведен список допустимых значений b для системы модулей 23, 19, 17, 13, 11, 7, 5, 3, 2.

Таблица
Таблица приблизительного деления
Если bi=0 для i ≠ p	Если bi≠0 для i≠p
bp	Q	bp	Q
1	1	1	2
2	2	2	3
3	3	3	5
4	5	4	5
5	5	5	3×2
6	3×2	6	7
7	5×2	7	5×2
8	5×2	8	5×2
9	5×2	9	5×2
10	5×2	10	11
11	11	11	13
12	13	12	13
13	13	13	7×2
14	7×2	14	5×3
15	5×3	15	17
16	17	16	17
17	17	17	19
18	19	18	19
19	12	19	7×3
20	7×3	20	7×3
21	7×3	21	7×3
22	11×2	22	23

Пример 1. В остаточной системе, состоящей из модулей 23, 19, 17, 13, 11, 7, 5, 3 и 2 (Р=223092870) делим a=10304312 на b=1401. Округленное частное .

Решение. Вначале представим b в обобщенной позиционной системе счисления в порядке уменьшаемой значимости b₉=0, b₈=0, b₇=0, b₆=0,

b₅=0, b₄=0, b₃=3, b₂=3, b₁=21, где b_i определяем из уравнения

b=b₉(23·19·17·13·11·7·5·3)+b₈(23·19·17·13·11·7·5)+b₇(23·19·17·13·11·7)+b₆(23·19·17·13·11)+b₅(23·19·17·13)+b₄(23·19·17)+b₃(23·19)+b₂23+b₁

Используя таблицу с b₁=b₃, получаем b₁==5·19·23=2185, так как b₁ является наиболее значимой ненулевой цифрой обобщенной позиционной системы счисления и определяется выражением где Q дано в таблице.

Отсюда: ;

Далее получаем остальные значения a_i и q_i

q3=607	a3=477698
q4=218	a4=172280
q5=78	a5=63002
q6=28	a6=23774
q7=10	a7=9764
q8=4	a8=4160
q9=1	a9=2759
q10=1	a10=1358

Так как q_r=0 (то есть q₁₁=0), но α_r-1≥b, то . Следовательно,

Полученный результат можно легко проверить обычным делением a=10304312 на b=1401. Для вычисления округленного частного потребовалось десять итераций, так как числа были выбраны обдуманно, чтобы получилось много операций. Это происходит в тех случаях, если a - относительно малое число, - аппроксимация b.

Модифицируем полученный алгоритм на язык кольцевых операций системы остаточных классов. Для этого рассмотрим следующий пример.

Пример 2. В остаточной системе, состоящей из модулей 7, 5, 3, 2 необходимо разделить число a=201→(5, 1, 0, 1) на число b=8→(1, 3, 2, 0).

Округленное частное обозначим как .

Решение. Вначале преобразуем делитель b в ОПСС в порядке уменьшаемой значимости:

b=b₄(7·5·3)+b₃(7·5)+b₂7+b₁, тогда b=0·(7·5·3)+0·(7·5)+1·7+1, где b₂=1, b₁=1.

Используя таблицу 1 с b_p=b₂ и b_i≠0 для i ≠ р, получим

где Q=2 или =2·7

Далее по алгоритму деления, изложенному выше, находим ,

где - это произведение двух модулей 7·2.

q₁=(0,4,2,0)→14.

Используя q_1, найдем

a₁=a₀-bq₁=(5,1,0,1) - (1,3,2,0·0,4,2,0)=(5,4,2,1)→89.

Далее получаем остальные значения a_i и q_i:

Так как то q₆=1. Следовательно, Действительно

Итак, для основного деления модулярных чисел, при котором делимое и делитель являются произвольными числами, необходимо выбрать приблизительный делитель, представленный в обобщенной позиционной системе счисления в виде простого числа или произведений простых чисел, на основе которых провести округление делимого с целью вычисления ошибки делимого с нулевым остатком, которые в дальнейшем используются в итерациях получения приблизительных и окончательных значений частного.

На чертеже представлена схема нейронной сети основного деления модулярных чисел.

Принцип работы данного изобретения излагается ниже.

Нейронная сеть основного деления модулярных чисел позволяет выполнить операцию деления при произвольных значениях делимого и делителя.

Делимое "a" и делитель "b", представленные в системе остаточных классов, поступают во входные регистры 1 и 2, соответственно, делимое по шине 3, а делитель по шине 4. Делитель b с выхода регистра 2 по шине 17 поступает на преобразователь кода системы остаточных классов в код обобщенной позиционной системы счисления (ОПСС) 6 (патент RU 3218238, опубликовано 27.02.2008, Бюл. №6) и на первый вход схемы умножения делителя b на промежуточное частное q_i 10. Делитель b, представленный в виде коэффициентов a_i в ОПСС, по шине 19 с выхода 6 поступает на адресные входы ПЗУ 7, реализующего нахождение в соответствии с таблицей. Далее, выбранные из ПЗУ значения приблизительного делителя, равного , в качестве разрешающего сигнала поступают по шине 22 на вход блока деления с нулевым остатком 5 (патент RU 3218239, опубликовано 27.02.2008, Бюл. №6), с выхода которого промежуточное частное q_i по информационной шине 28 поступает на второй вход блока умножения 10 и на входы сумматора 8 и схемы сравнения 9.

Если q_i=0, то схема сравнения 9 формирует сигнал управления "Да", который по шине 24 через ключ 13, выход которого по шине 25 поступает на управляющий вход сумматора 8, на выходе которого, шина 15, формируется результат деления.

Если q_i≠0, то схема сравнения 9 формирует сигнал управления "Нет", который по шине 23 поступает на разрешающий вход схемы запрета 14, которая разрешает прохождение по шине 18 промежуточного значения a_i на вход регистра 1 по шине 21. Кроме того, сигнал "Нет" разрешает умножение промежуточного частного q_i на делитель "b", поступающий по шине 17.

Результат умножения в блоке 10 по шине 20 поступает на первый вход блока вычитателя 11, на второй вход которого поступает значения a_i по шине 16 с выхода регистра 1. Результат вычитания по шине 18 поступает на вход схемы сравнения с ^b/₂ блока 12 и на информационный вход схемы запрета 14, с выхода которого по шине 21 a_i подается на вход регистра 1. Кроме того, a_i сравнивается с ^b/₂ блока 12, если формируется сигнал "нет", то схема сравнения 12 выдает управляющий сигнал, который по шине 27 через ключ 13 и шину 25 считывает результат деления, шина 15, который сформирован в накапливающем сумматоре 8, если схема сравнения 12 формирует сигнал "Да", то схема сравнения выдает сигнал "1", который по шине 26 подается на вход сумматора, где суммируется с содержимым сумматора 8, на выходе которого просуммированные частные q_i выдаются на выход, шина 15, которые являются выходом нейронной сети основного деления модулярных чисел.

Время деления определяется количеством итераций, которые выполняются за четыре цикла синхронизации.

Нейронная есть основного деления модулярных чисел, содержащая входные регистры делимого и делителя, на входы которых подаются соответственно делимое и делитель, представленные в системе остаточных классов (СОК), выходы входного регистра делимого соединены с входами блока деления с нулевым остатком, выполненного в виде нейронной сети для деления чисел в СОК, и входом блока вычитателя, который реализует вычислительную модель a_i-b_qi, где а_i - исходное или промежуточное значение делимого, b - значение делителя и q_i - промежуточное частное, выходы входного регистра делителя соединены с входом блока преобразования остаточного кода в код обобщенной позиционной системы счисления (ОПСС), выполненного в виде нейронной сети, и первым входом блока умножения, который реализует вычислительную модель b_qi, отличающаяся тем, что выходы блока преобразования остаточного кода в код ОПСС соединены с адресными входами постоянного запоминающего устройства, в котором хранятся значения приблизительного делителя где Q - коэффициент, являющийся простым числом, для выбранного набора модулей СОК, a p_i - значения модулей или их произведений, выходы которого соединены с входами блока деления с нулевым остатком, выходы которого соединены со вторыми входами блока умножения, информационными входами сумматора и схемы сравнения с нулем, выход схемы сравнения с нулем, на котором формируется сигнал «Нет», соединен с разрешающим входом блока запрета и разрешающим входом блока умножения, выход которого соединен с первым входом блока вычитания, выход которого соединен с информационным входом блока запрета и входом блока сравнения с величиной b/2, выход указанного блока, на котором формируется сигнал «Нет», соединен с управляющим входом ключа, второй вход которого соединен с выходом схемы сравнения с нулем, на котором формируется сигнал «Да», выход ключа соединен с управляющим входом сумматора, выход блока сравнения с величиной b/2, на котором формируется сигнал «Да», соединен с входом сумматора для добавления единицы к содержимому сумматора, выходы которого являются выходами нейронной сети основного деления модулярных чисел, выход блока запрета, на котором формируется промежуточное значение делимого q_i, соединен с входом входного регистра делимого.