Способ прогнозирования разрушения

Способ прогнозирования разрушения

Иллюстрации

Показать все

Реферат

Область техники

[0001] Настоящее изобретение относится к способу и устройству, а также программному продукту и носителю информации для прогнозирования разрушения тонкой пластины, выполненной из металлического материала, и оно особенно предпочтительно в качестве критерия определения разрушения в случае разрушения материала в процессе повреждения при аварии автомобильной детали, подвергнутой прессованию (штамповке).

Уровень техники

[0002] Предел разрушения определяется, вообще говоря, с использованием критерия утонения или диаграммы предельного деформирования (ДПД) (от англ. «forming limit diagram», FLD). ДПД указывает главную и второстепенную деформацию (ε₁ и ε₂ соответственно), при которой происходит разрушение, и может использоваться в анализе повреждений при аварии (т.н. «краш-анализе»). ДПД может быть экспериментально определена посредством нагружения образцов по различным пропорциональным траекториям. Наказима (Nakazima) и др., например, применяли вытягивание полусферическим пуансоном для прямоугольных образцов с различными ширинами. Перед операцией формовки на поверхность листа наносят маленькие разметочные кольца или сетки посредством гравировки или печатания. Эти кольца искажаются в эллипсы во время операции формовки, которая заканчивается при начале образования шейки или трещины. Размер эллипса вблизи шейки варьируется с шириной образца. Главную и второстепенную деформации измеряют по эллипсу у шейки или трещины. Наконец, предельную кривую деформирования (ПКД) проводят так, чтобы она устанавливала измеренные предельные деформации для различных траекторий.

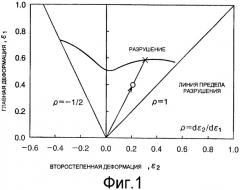
[0003] На фиг.1 показана измеренная при эксперименте предельная кривая разрушения. В качестве способа прогнозирования ДПД используется объединение критериев Хилла (Hill) и Свифта (Swift), модель Маркиньяк-Кусчински (Marciniak-Kuczynski), модель Сторен-Райса (Storen-Rice) и т.п., и ДПД может быть получена посредством коррекции влияния толщины листа по эмпирическому правилу Килера. Разрыв может быть произведен посредством динамического кода конечных элементов, тогда как первый не может быть обнаружен при конечноэлементных анализах. Вместо прямых предсказаний разрыва, рассчитанные деформации сравнивают с критическими значениями, внешне заданными, и считается, что разрушение происходит тогда, когда одна из рассчитанных деформаций достигает предела.

[0004] Непатентный документ 1: Journal of the Japan Society for Technology of Plasticity, 45, 123, 2004.

Непатентный документ 2: CAMP-ISIJ 17, 1063, 2004.

Непатентный документ 3: Metal Forming, Hosford, 319, 1993.

Непатентный документ 4: Transactions of the Japan Society of Mechanical Engineers, Series A, 54, 1617, 1998.

Сущность изобретения

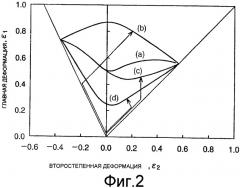
[0005] Схематическая иллюстрация экспериментальных предельных деформаций при формовке для (a) пропорционального нагружения, (b) одноосного растяжения с последующим равно-двухосным растяжением, (c) равно-двухосного растяжения с последующим растяжением при плоской деформации и (d) равно-двухосного растяжения с последующим одноосным напряжением приведена на фигуре 2. На фигуре 2 показано, что максимальная кривая наблюдается при одноосном растяжении с последующим равно-двухосным растяжением, тогда как минимальная кривая получается для противоположной последовательности. ПКД для равно-двухосного растяжения с последующим растяжением при плоской деформации несколько выше, чем эта минимальная кривая.

[0006] В процессе деформирования при аварии детали кузова автомобиля, подвергнутой прессованию или предварительному деформированию при прессовании, траектория деформации часто изменяется. При оценке разрушения с использованием полученных при эксперименте предельных деформаций при формовке эти предельные деформации при формовке должны быть получены заранее по бесконечному числу траекторий деформации. Поэтому на практике для оценки разрушения необходимо использовать значение предельной деформации при формовке относительно траектории пропорционального нагружения и, следовательно, нельзя ожидать высокой точности прогнозирования.

[0007] Кроме того, разрушение стальных листов происходит при растягивающем загибании кромок, когда деформация растяжения в окружном направлении обрезной кромки достигает критического значения. Напряженное состояние на участке обрезной кромки близко к одноосному растяжению, но имеются резкие градиенты напряжения и деформации внутрь от участка обрезной кромки. Таким образом, предел разрушения указывает значение, которое довольно сильно отличается от предела деформации или напряжения разрушения, полученного при испытании на одноосное растяжение. Конкретнее, высокопрочные стали с прочностью свыше 590 МПа «страдают» разламыванием при отбортовке кромок, даже когда участок обрезной кромки достигает пластической неустойчивости и возникает локальное утонение (образование шейки по толщине), внутренний материал, исключая участок обрезной кромки, все еще не достигает пластической неустойчивости. Таким образом, будучи ограниченной внутренним материалом, пластическая неустойчивость не может быть достигнута в целом, и продвижение локализованного утонения задерживается.

[0008] Кроме того, при пределе растягивающего загибания кромок в окружном направлении участка обрезной кромки образуется большое количество шеек по толщине, и, таким образом, разрушение задерживается. Например, предполагая, что в одном положении участка обрезной кромки образовалось локализованное утонение, напряжение в окружном направлении вблизи локализованного утонения ослабляется. Однако влияние этого ослабления напряжения уменьшается с расстоянием от локализованного утонения, и когда деформирование протекает далее, образуется следующее локализованное утонение в местоположении, отделенном от первого локализованного утонения. Когда деформирование протекает еще далее, образуется новое утонение (шейка). Повторяя этот процесс, в окружном направлении участка обрезной кромки образуется большое количество шеек, и локализованное утонение растет. В данном случае причина, по которой ранее образовавшиеся шейки по толщине листа растут, но не приводят к разрушению, заключается в том, что они сдерживаются материалом, имеющим малую деформацию, и не удовлетворяют пластической неустойчивости, как весь участок обрезной кромки в окружном направлении. Поэтому при пределе растягивающего загибания, когда в одном положении в окружном направлении участка обрезной кромки образуется шейка по толщине, она не приводит к разрушению, но замедляется.

[0009] Таким образом, способ прогнозирования предела растягивающего загибания (отбортовки) кромок непрост из-за существования градиента деформации, направленного внутрь от участка обрезной кромки, и из-за эффекта замедления, так что разрушение не происходит, даже когда одно положение в окружном направлении удовлетворяет локализованному утонению. Таким образом, до настоящего времени такой способ еще не предложен.

[0010] Настоящее изобретение направлено на решение вышеуказанных технических проблем в существующем уровне техники, и задача изобретения состоит в том, чтобы предоставить способ прогнозирования разрушения, посредством которого при прогнозировании наличия возникновения разрушения в стальном листе в процессе, включающем в себя одну или более траекторий деформации, может быть легко и эффективно получена предельная кривая разрушения, и появление разрушения может быть спрогнозировано с высокой точностью прогнозирования, и риск разрушения при прессовании или стойкость к ударным нагрузкам могут быть оценены количественно, тем самым реализуя эффективную и высокоточную разработку кузовов автомобилей, оптимизируя при этом материал, формовку и конструкции кузова автомобиля для безопасности при аварии.

[0011] Способ прогнозирования разрушения по настоящему изобретению представляет собой способ оценки предела разрушения тонкой пластины из металлического материала, и этот способ включает в себя, при прогнозировании возникновения разрушения в тонкой пластине в процессе пластического деформирования в соответствии с одним или более изменениями траектории деформирования, процедуру преобразования предельной кривой разрушения в пространстве деформаций в предельную кривую разрушения в пространстве напряжений и процедуру прогнозирования наличия возникновения разрушения с использованием полученной предельной кривой разрушения в пространстве напряжений.

[0012] Кроме того, в результате специальных исследований для решения вышеуказанных проблем авторы настоящего изобретения разработали несколько следующих аспектов изобретения. Ясно показано, что прогнозирование с высокой точностью возможно за счет использования в качестве критерия разрушения коэффициента раздачи отверстия, имеющего хорошую корреляцию с пределом растягивающего загибания кромок, и, кроме того, посредством выполнения определения разрушения в пространстве напряжений, в котором можно учесть влияние деформационной предыстории, вместо пространства деформаций.

[0013] Кроме того, в результате специальных исследований для решения вышеуказанных проблем авторы настоящего изобретения разработали несколько следующих аспектов изобретения. Способ получения предела разрушения по настоящему изобретению представляет собой способ получения предела разрушения, используемого для определения предела разрушения тонкой пластины, выполненной из металлического материала, в котором коэффициент λ деформации растяжения, полученный из испытания на раздачу отверстия, преобразуют в предельную кривую разрушения в пространстве напряжений при определении предела разрушения тонкой пластины в процессе, включающем в себя одну или более вариаций траектории деформирования.

[0014] Предельная кривая разрушения, выраженная в пространстве напряжений, не зависит от траектории деформирования и, следовательно, может быть выражена единственной предельной кривой. Поэтому, используя ее в качестве критерия определения разрушения, разрушение на участке растягивающего загибания кромок, включающем в себя одну или более вариаций траектории деформирования, можно определить с высокой точностью.

[0015] В соответствии с настоящим изобретением, прогнозируя наличие возникновения разрушения в тонкой пластине в процессе, включающем в себя одну или более вариаций траектории деформирования, возможно получить предельную кривую разрушения легко и эффективно и спрогнозировать наличие возникновения разрушения с высокой точностью прогнозирования. Таким образом, риск разрушения при прессовании или аварии может быть оценен количественно, тем самым реализуя эффективную и очень точную разработку автомобильного кузова, одновременно учитывающую материал, способ конструирования и саму конструкцию.

Краткое описание чертежей

[0016] Фиг.1 - диаграмма, показывающая диаграмму предельного деформирования (ДПД), используемую для пояснения традиционного уровня техники.

Фиг.2 - диаграмма предельного деформирования, используемая для пояснения проблем, решаемых настоящим изобретением.

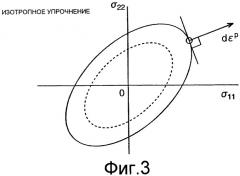
Фиг.3 - диаграмма для пояснения преобразования от деформации к напряжению.

Фиг.4 - диаграмма для пояснения закона преобразования координат.

Фиг.5 - диаграмма, показывающая, что, в то время как ДПД в пространстве деформаций зависит от траектории деформирования и ее предельная кривая разрушения значительно варьируется, предельная кривая разрушения в пространстве напряжений может быть выражена единственной кривой.

Фиг.6 - диаграмма, показывающая соотношение между ходом пуансона и максимальной главной деформацией.

Фиг.7 - диаграмма, показывающая сравнение точности прогнозирования при выполнении численного моделирования с различными условиями анализа и с использованием ДПД, полученной при эксперименте, и пределом возникновения локализованного утонения в качестве критерия определения разрушения.

Фиг.8 - диаграмма, показывающая позиционное соотношение между предысторией напряжения в процессе формовки, полученной численным моделированием, и предельной кривой разрушения.

Фиг.9 - диаграмма, показывающая точность прогнозирования способа по настоящему изобретению.

Фиг.10 - диаграмма, показывающая деталь с тавровым профилем сечения, которая является объектом проверки точности прогнозирования при краш-анализе, и общий вид трехточечного испытания на изгиб падающим грузом.

Фиг.11 - диаграмма, показывающая результат анализа формовки вытяжкой с изгибом таврового профиля посредством численного моделирования.

Фиг.12 - диаграмма, показывающая соотношение между эквивалентной пластической деформацией и эквивалентным напряжением в соответствии со скоростью деформации.

Фиг.13 - диаграмма, показывающая позиционное соотношение между предельной кривой динамического напряжения разрушения в пространстве напряжений и динамическим напряжением, полученным при моделировании аварии.

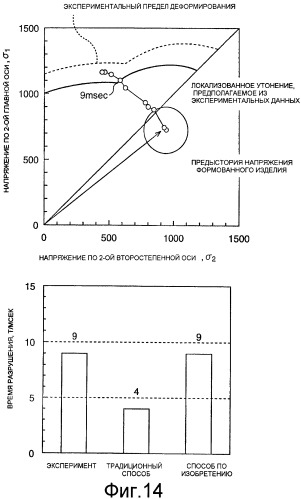
Фиг.14 - диаграмма, показывающая позиционное соотношение между предысторией напряжения в процессе формовки, полученной численным моделированием, и предельной кривой разрушения и точность прогнозирования способа по настоящему изобретению.

Фиг.15 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой, поясняющей экспериментальный способ.

Фиг.16 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой, поясняющей модель анализа.

Фиг.17 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся контурной диаграммой, отображающей результат анализа относительно распределения главной деформации.

Фиг.18 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой, показывающей соотношение между расстоянием от края отверстия и максимальной главной деформацией в связи с результатом анализа.

Фиг.19 - диаграмма, используемая для пояснения примера по настоящему изобретению, причем она является диаграммой, показывающей соотношение между расстоянием от края отверстия и максимальной главной деформацией в связи с результатом анализа.

Фиг.20 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой, показывающей позиционное соотношение между предысторией напряжения в процессе формовки, полученной численным моделированием, и линией предельного напряжения возникновения утонения.

Фиг.21 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой, показывающей позиционное соотношение между предысторией напряжения в процессе формовки, полученной численным моделированием, и кривой предельного напряжения возникновения утонения, и критерием определения разрушения, полученным преобразованием коэффициента раздачи отверстия в пространство напряжений.

Фиг.22 - блок-схема, показывающая основную структуру устройства прогнозирования разрушения в соответствии с этим примером.

Фиг.23 - блок-схема последовательности операций, показывающая этапы выполнения прогнозирования разрушения в процессе формовки тонкой пластины из металлического материала, со способом прогнозирования разрушения в соответствии с этим примером.

Фиг.24 - блок-схема последовательности операций, показывающая этапы выполнения прогнозирования разрушения в процессе повреждения, продолженная из схемы прогнозирования разрушения на этапе формовки по фиг.23, со способом прогнозирования разрушения в соответствии с этим примером.

Фиг.25 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой предельного деформирования (ДПД), измеренной при эксперименте.

Фиг.26 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой предельного деформирования (ДПД), учитывающей влияние толщины стали с использованием правила коррекции Килера на толщину стали по отношению к предельной кривой пластической неустойчивости, спрогнозированной по теории Хилла-Свифта и модели Сторен-Райса.

Фиг.27 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой предельного деформирования (ДПД), спрогнозированной с использованием закона зависимости приращения напряжения, исходя из модели Сторен-Райса.

Фиг.28 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой, поясняющей преобразование от деформации к напряжению.

Фиг.29 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой, показывающей, что, в то время как ДПД пространства деформации зависит от траектории деформирования и предел разрушения на ней значительно варьируется, предельная кривая разрушения в пространстве напряжений может быть выражена единственной кривой.

Фиг.30 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой, поясняющей экспериментальный способ.

Фиг.31 - диаграмма, используемая для пояснения примера по настоящему изобретению и являющаяся диаграммой, показывающей линию предельного напряжения разрушения, выражающую коэффициент раздачи отверстия в пространстве напряжений.

Фиг.32 - блок-схема, показывающая основную структуру устройства получения предела разрушения в соответствии с примером 1.

Фиг.33 - блок-схема последовательности операций, показывающая этапы способа получения предела разрушения в соответствии с примером 1.

Фиг.34 - блок-схема, показывающая основную структуру устройства получения предела разрушения в соответствии с примером 2.

Фиг.35 - блок-схема последовательности операций, показывающая этапы способа получения предела разрушения в соответствии с примером 2.

Фиг.36 - блок-схема, показывающая основную структуру устройства получения предела разрушения в соответствии с примером модификации примера 2.

Фиг.37 - схематическая диаграмма, показывающая внутреннюю структуру персонального пользовательского терминального устройства.

Подробное описание предпочтительных вариантов реализации

Первый вариант реализации

[0017] Запас до разрушения при оценке формуемости определяется обычно с использованием критерия утонения или ДПД, что также может быть использовано для прогнозирования разрушения при краш-анализе автомобиля. При этом известно, что ДПД значительно изменяется в зависимости от изменений траектории деформирования, и поэтому нельзя ожидать, что она будет иметь высокую точность прогнозирования в качестве способа оценки разрушения в процессе пластического деформирования, при котором траектория деформирования значительно изменяется, как при поломке детали автомобильного кузова, подвергнутой прессованию или предварительному деформированию при прессовании.

[0018] Вместе с тем, недавно Кувабара (Kuwabara) и др. (см. непатентные документы 1, 2) подтвердили посредством эксперимента и анализа, что, используя предельную кривую разрушения, выраженную в пространстве напряжений для случая экструдированного алюминиевого материала или мягкой листовой стали в качестве объекта, предел разрушения может быть представлен почти однозначно, без зависимости от траектории деформирования. Эти сведения относятся к алюминию или мягкой листовой стали и не прояснены для высокопрочных сталей с прочностью свыше 440 МПа и, следовательно, не могут использоваться для современной разработки автомобильного кузова, в котором главным образом используются листы из высокопрочной стали.

[0019] Соответственно, авторы настоящего изобретения впервые добились следующих позиций.

(1) Когда детальный эксперимент выполняют на листах из высокопрочной стали, имеющих прочность на растяжение 440 МПа или выше, и используют предельную кривую разрушения, выраженную в пространстве напряжений, предел разрушения может быть выражен единственной предельной кривой разрушения без зависимости от траектории деформирования.

(2) При использовании предельной кривой разрушения, выраженной в пространстве напряжений, возможно с высокой точностью спрогнозировать оценку разрушения в процессе пластического деформирования, при котором траектория деформирования значительно изменяется, как при поломке детали автомобильного кузова, подвергнутой прессованию или предварительному деформированию при прессовании.

Примеры

[0020] Ниже на основе различных примеров будет подробно рассмотрен первый вариант реализации.

Пример 1

[0021] Сначала будет пояснен способ получения предельной кривой разрушения в пространстве напряжений. Используя в качестве объекта стальной лист, показанный в таблице 1, измерили (1) предельную деформацию разрушения на траектории пропорционального нагружения и (2) предельную деформацию разрушения при вариации траектории деформирования. Здесь t обозначает толщину тонкой пластины, YP обозначает условный предел текучести, TS обозначает предел прочности на растяжение, U.El обозначает равномерное удлинение, El обозначает полное удлинение, r_m обозначает среднее значение r (указывающее значение Лэнкфорда и выражаемое как r_m=(r₀+2r₄₅+r₉₀)/4, где r₀ - значение r в направлении прокатки, r₄₅ - значение r в направлении под 45° относительно направления прокатки, и r₉₀ - значение r в направлении под 90° относительно направления прокатки), а K, ε₀, n обозначают параметры материала, полученные в том случае, когда кривая напряжение-деформация, полученная из испытания на одноосное растяжение, аппроксимирована выражением функции

[Уравнение 1]

.

[0022] Для предельной деформации разрушения на траектории пропорционального нагружения деформацию разрушения измеряли при диаметре разметочной окружности 6 мм одноосным растяжением, способом Накаджима (вытягивание полусферическим пуансоном с использованием листа Тефлона (зарегистрированный товарный знак)) и испытанием на гидравлическое выгибание. С другой стороны, для предельной кривой разрушения при изменениях траектории деформации, после того как выполнили 10%-ное растяжение вдоль направления прокатки в качестве первого деформирования, деформацию разрушения измеряли одноосным растяжением и способом Накаджима так, чтобы направление под углом 90° относительно направления первичной раздачи соответствовало максимальному основному напряжению.

[0023]

[Таблица 1]
ЗНАЧЕНИЯ МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛА И ПАРАМЕТРЫ МАТЕРИАЛА
t/мм	YP	TS	U.El	El	rm	K	ε0	n
1,2	460	598	12	23	1,00	937	0,0108	0,157
(Единицы: t - мм; YP, TS, K - МПа; El, U.El - %)

[0024] Преобразование от деформации к напряжению становится возможным в предположении (1) несжимаемости, (2) функции текучести Мизеса, (3) закона изотропного упрочнения материала, (4) принципа нормальности и (5) безмоментного состояния напряжения. Далее будет пояснен конкретный способ преобразования предельной кривой разрушения в пространстве деформаций в пространство напряжений.

[0025] ДПД пространства деформации - это диаграмма, показывающая главную деформацию ε₁₁, дающую предел разрушения для каждой второстепенной деформации ε₂₂, и по ним и закону постоянного объема может быть получена деформация по толщине ε₃₃:

[Уравнение 2]

.

Обычно если используется уравнение состояния материала при анализе формовки или краш-анализе, то используется закон изотропного упрочнения, предполагающий, что эквивалентное пластическое напряжение σ_eq является однозначной функцией эквивалентной пластической деформации ε_eq независимо от траектории деформирования и может быть отображено с использованием закона деформационного упрочнения Свифта в виде

[Уравнения 3]

.

В качестве функции деформационного упрочнения может быть использовано, например, полиномиальное выражение высокой степени эквивалентной пластической деформации или выражение другого вида, но предпочтительно использовать уравнение Свифта, которое дает хорошее приближение и часто используется в численном моделировании тонколистовой стали.

[0026] При использовании функции текучести Мизеса для поверхности текучести, например, эквивалентная пластическая деформация ε_eq может быть представлена в виде

[Уравнения 4]

и может быть получена с использованием анизотропного критерия Хилла в случае плоской изотропии посредством

[Уравнения 5]

.

При использовании функции анизотропной текучести Хилла требуется значение параметра r пластической анизотропии, которое может быть получено специально как r=(r₀+2r₄₅+r₉₀)/4 из значений r (r₀, r₄₅, r₉₀) в направлениях 0°, 45°, 90° относительно направления прокатки.

[0027] Кроме того, при необходимости может использоваться функция анизотропной текучести высокой степени, однако она имеет много параметров и требует учета направления на поверхности пластины при обработке и, следовательно, обеспечивает недостаточное улучшение точности, даже несмотря на то, что она усложнена. Таким образом, на практике достаточно функции текучести в предположении плоскостной изотропии (изотропной плоскости). В любой функции текучести эквивалентное пластическое напряжение σ_eq, учитывающее вариацию траектории деформирования, может быть получено с использованием эквивалентной пластической деформации ε_eq, полученной интегрированием приращения dε_eq эквивалентной пластической деформации по траектории деформирования и с помощью закона деформационного упрочнения.

[0028] Затем компонента σ_ij отклонения напряжения получается посредством изотропного упрочнения поверхности текучести, показанной на фиг.3, и принципа нормальности:

[Уравнение 6]

.

Наконец, предполагая плоское напряжение (σ₃₃=0), компонента напряжения σ'_ij может быть получена из

[Уравнения 7]

.

[0029] Следует отметить, что когда главная ось деформации и направление прокатки не совпадают, как показано на фиг.4, необходима операция преобразования координат, показанная ниже. На диаграмме x_i обозначает ось x₁//RD, ось x₂//TD, ось x₃//ND, которые являются координатными осями системы координат материала, а X_i обозначает главную ось деформации в деформации n-го порядка. Если в системе координат материала отображение компоненты тензора A есть Â_ij, а тензор с преобразованными координатами есть R, то (1) компонента деформации ε_ij, измеренная посредством экспериментальной системы координат, может быть преобразована в компоненту деформации

[Уравнение 8]

,

причем система координат материала является опорной системой координат в соответствии с законом преобразования координат. Затем компонента отклонения напряжения получается из (2) функции текучести, смоделированной с системой координат материала, являющейся опорной системой координат, и критерием нормальности, и, наконец, (3) закон преобразования координат используется для получения компоненты напряжения

[Уравнение 9]

с экспериментальной системой координат, являющейся опорной системой координат.

[0030] На фиг.5 показана ДПД, измеренная в эксперименте, и предельная кривая разрушения, полученная преобразованием ДПД в пространство напряжений с главным напряжением и второстепенным напряжением посредством вышеупомянутого способа. ДПД пространства деформации зависит от траектории деформирования, и предельная кривая разрушения значительно изменяется, но предельная кривая разрушения, выраженная в пространстве напряжений, становится единственной предельной кривой разрушения.

[0031] Кроме того, авторы настоящего изобретения продемонстрировали, что в результате выполнения экспериментов и исследований на листах высокопрочной стали классов прочности от 440 МПа до 980 МПа, показанных ниже в таблице 2, независимо от прочности материала на растяжение или механизма упрочнения, получаются единственные предельные кривые разрушения в широком диапазоне. Используя эти предельные кривые разрушения, выраженные в пространстве напряжений, оценка разрушения в процессе пластического деформирования, при котором траектория деформирования значительно изменяется, как при повреждении детали автомобильного кузова, подвергнутой прессованию или предварительному деформированию при прессовании, может быть спрогнозирована с высокой точностью.

[0032] Следует отметить, как само собой разумеющееся, что может быть использована предельная кривая разрушения, полученная преобразованием ДПД, измеренной экспериментальным способом, отличным от способа Накаджима, в пространство напряжений, или же для прогнозирования разрушения может быть использована предельная кривая разрушения, полученная преобразованием теоретической ДПД по модели локализованного утонения Хилла, модели размытого утонения Свифта, методу Маркиньяк-Кусчинского, модели Сторен-Райса или им подобных в пространство напряжений.

[0033]

[Таблица 2]
ЗНАЧЕНИЯ МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛА И ПАРАМЕТРЫ МАТЕРИАЛА
МАТЕРИАЛ	t	YP	TS	U.El	El
A: ТВЕРДОРАСТВОРНО-УПРОЧНЕННАЯ СТАЛЬ 440 МПа	1,2	368	460	18	35
B: ДИСПЕРСИОННО-УПРОЧНЕННАЯ СТАЛЬ 590 МПа	1,2	460	598	12	23
C: ДВУХФАЗНАЯ СТАЛЬ 780 МПа	2,0	490	840	10	19
D: ДВУХФАЗНАЯ СТАЛЬ 980 МПа	2,0	710	1010	8	14
(Единицы: t - мм; YP, TS - МПа; El, U.El - %)

[0034] Далее будет пояснен способ оценки предела разрушения. При прогнозировании разрушения материала численным моделированием методом конечных элементов (МКЭ) возникают следующие технические проблемы.

(1) На ДПД, измеренную в эксперименте, сильно влияет расстояние между точками оценки и режим трения. Таким образом, при использовании ДПД в качестве критерия определения разрушения требуется коррекция согласно условиям анализа численного моделирования.

(2) В численном моделировании увеличение деформации вплоть до равномерной деформации может быть смоделировано точно, но для моделирования локализованного утонения, возникающего в некоторой области вплоть до толщины листа или полосы скольжения, в которой деформация локализована в более узкой области, конечные элементы должны быть адекватно сегментированы. Таким образом, при производительности современных компьютеров прогнозирование является трудным.

(3) С уравнением состояния материала, используемым обычно в универсальных программных средствах, локализация деформации задерживается, и, следовательно, оценка с точки зрения риска дается в том случае, когда в качестве критерия определения разрушения принимается фактически измеренная ДПД.

[0035] В результате специальных исследований этих проблем авторы настоящего изобретения прояснили критерий определения разрушения, подходящий для численных моделирований. Пользуясь в качестве объектов стальными листами, показанными в таблице 1, выполнили численное моделирование МКЭ вытягивания полусферическим пуансоном и изучили влияния размера элемента и уравнения состояния материала на процесс локализации деформации.

[0036] На фиг.6 показано соотношение максимальной главной деформации, произведенной ходом пуансона и прессованием. Влияния размера элемента и уравнения состояния материала почти не сказываются от начала формовки до хода пуансона в приблизительно 25 мм, но эти влияния становятся заметными выше 25 мм, где начинается локализация деформации.

[0037] На фиг.7 показано сравнение точности прогнозирования при выполнении численного моделирования с различными условиями анализа и с использованием ДПД, полученной в эксперименте, и пределом возникновения локализованного утонения в качестве критерия определения разрушения. Когда в качестве критерия определения разрушения используется фактически измеренная ДПД, процесс локализации деформации нельзя точно смоделировать, и, таким образом, точность прогнозирования разрушения невысока. С другой стороны, когда в качестве предела разрушения используется предел возникновения локализованного утонения, прогнозирование становится возможным с относительно высокой точностью независимо от размера элемента и используемого уравнения состояния материала, и может быть получена оценка с точки зрения безопасности. Это предполагает, что предел возникновения локализованного утонения может быть на практике использован в качестве критерия определения разрушения, потому что вязкое разрушение в стальном листе происходит в том положении, где локализуется деформация при локализованном утонении, и когда возникает локализованное утонение, оно приводит к разрушению за очень короткое время.

[0038] Предел возникновения локализованного утонения может рассматриваться в рамках пластической неустойчивости и может быть спрогнозирован посредством теоретической ДПД по модели локализованного утонения Хилла, модели размытого утонения Свифта, методу Маркиньяк-Кусчинского, модели Сторен-Райса или им подобным.

[0039] Как показано в этом конкретном примере, в результате специальных исследований авторы настоящего изобретения обнаружили, что высокая точность прогнозирования может быть гарантирована при использовании в качестве критерия определения разрушения предельной кривой разрушения, полученной преобразованием кривой начала утонения в пространстве деформаций в пространство напряжений при оценке разрушения с помощью численного аналитического моделирования с использованием метода конечных элементов.

[0040] Далее будет пояснен конкретный пример способа оценки предела разрушения. Показывается конкретный пример прогнозирования разрушения на нелинейной траектории, например такой, что, используя в качестве объектов стальные листы, показанные в таблице 1, в качестве первого деформирования выполняют 10%-ное одноосное растяжение в направлении прокатки и после этого выполняют деформирование в условиях плоской деформации вытягиванием полусферическим пуансоном. На фиг.8 показано соотношение между предысторией напряжения в процессе формовки, полученной численным моделированием, и предельной кривой разрушения, полученной преобразованием кривой начала утонения в пространстве деформаций в пространство напряжений.

[0041] При использовании явного динамического метода численного моделирования полученное напряжение увеличивается, значительно колеблясь, поскольку распространение волны напряжения решается при минутных временных интервалах, без выполнения повторного вычисления в пределах временного шага. При этом способе сравнения позиционного соотношения между напряжением и предельным напряжением разрушения для оценки разрушения затруднительно обеспечить высокую точность прогнозирования.

[0042] В результате специальных исследований авторы настоящего изобретения изобрели способ определения разрушения с высокой точностью, при котором можно избежать, используя явный динамический метод численного моделирования, колебания напряжения путем преобразования пластической деформации в напряжение посредством последующей обработки.

[0043] На фиг.9 показаны результаты прогнозирования разрушения способом по настоящему изобретению. При обычном способе прогнозирования разрушения посредством ДПД прогнозирование с высокой точностью затруднено, поскольку предельная кривая разрушения значительно варьируется в зависимости от траектории деформирования. Напротив, применяя настоящее изобретение, можно видеть, что разрушение может быть спрогнозировано с хо