Способ определения постоянных времени формирования пограничного слоя упруго опертой жесткой пластины при дозвуковом обтекании

Способ определения постоянных времени формирования пограничного слоя упруго опертой жесткой пластины при дозвуковом обтекании

Иллюстрации

Показать все

Реферат

Изобретение относится к области теории управления, а именно к способам определения постоянных времени формирования пограничного слоя упруго опертой жесткой пластины на основе оценки устойчивости упругих пластин при дозвуковом обтекании потоком газа, и может быть использовано в авиационной технике.

Точные решения уравнений пограничного слоя были получены только в некоторых простейших случаях. Блазиусом и Хоуэрзом был разработан метод расчета пограничного слоя, основанный на представлении решения в виде степенного ряда. Однако расчет пограничного слоя по этому методу связан со значительной вычислительной работой. Существующие приближенные методы расчета пограничного слоя сводятся либо к приближенным способам решения дифференциальных уравнений Прандтля, либо к использованию интегрального соотношения, установленного Карманом. Среди интегральных методов наибольшее распространение получили методы Польгаузена, Кочина и Лойцянского.

Известен способ оценки постоянных времени формирования пограничного слоя, принятый за прототип (см. В.В.Струминский. Теория нестационарного пограничного слоя. - М.: Государственное издательство оборонной промышленности, 1957).

В указанном способе за аппереодическое звено выбрана толщина пограничного слоя и граница его распространения по ширине профиля. А в данной работе за аппереодическое звено берется эффективный угол атаки, который определяется скоростью распространения толщины пограничного слоя по ширине профиля.

Если тело совершает установившееся движение и в некоторый момент времени это движение нарушается, например внезапно меняется угол атаки крыла, то переход к новому установившемуся движению, соответствующему новому положению крыла в потоке, не происходит столь же быстро, как изменение угла атаки, а запаздывает (Лойцянский Л.Г. Ламинарный пограничный слой / Л.Г.Лойцянский // М.: Государственное издательство физико-математической литературы. - 1962. - 480 с., с.114).

В основу работы положен способ оценки устойчивости упруго опертой жесткой пластины - определение критической скорости флаттера с использованием датчика перемещений (вибраций), установленного на пластине, и осциллографа, подключенного к цепи измерения, содержащий датчик перемещений (вибраций). Дальнейшее определение постоянных времени формирования пограничного слоя, используя полученное значение критической скорости флаттера и нелинейный частотный критерий устойчивости (Санкин Ю.Н. Частотный критерий устойчивости нелинейных замкнутых систем, включающих вязкоупругое звено с распределенными параметрами / Ю.Н.Санкин // Труды СВМО, 2005, Т.7, №1 / УДК 621.9-05).

К причинам, препятствующим достижению указанного ниже результата, относится значительная сложность вычислительных работ. Учет постоянных времени формирования пограничного слоя на несущих плоскостях летательного аппарата позволяет уточнить допустимые режимы маневрирования по сравнению с тем, что дает модель обтекания без учета постоянных времени формирования пограничного слоя.

Технический результат - создание методики определения постоянных времени формирования пограничного слоя упруго опертой жесткой пластины при дозвуковом обтекании потоком газа, посредством методов теории управления, основанное на учете скорости флаттера (возникновение неустойчивого движения), что позволяет создать методы расчета динамики летательного аппарата в условиях интенсивного маневрирования.

Динамические характеристики летательного аппарата изменяются в зависимости от скорости движения (особенно на малых скоростях полета и при интенсивном маневрировании), когда постоянная времени формирования пограничного слоя оказывают существенное влияние на эти характеристики.

Математическая модель заключается в следующем: определение постоянных времени формирования пограничного слоя и влияние их на флаттер и управление летательным аппаратом. Заявленное изобретение поясняется чертежами.

На фиг.1. - АФЧХ амплитуд изгибных колебаний;

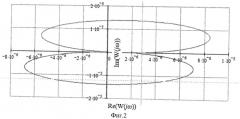
на фиг.2. - АФЧХ амплитуд крутильных колебаний;

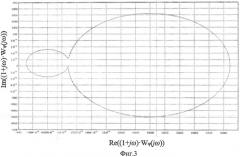
на фиг.3. - Зависимость (1+jω)·W_ψ(jω);

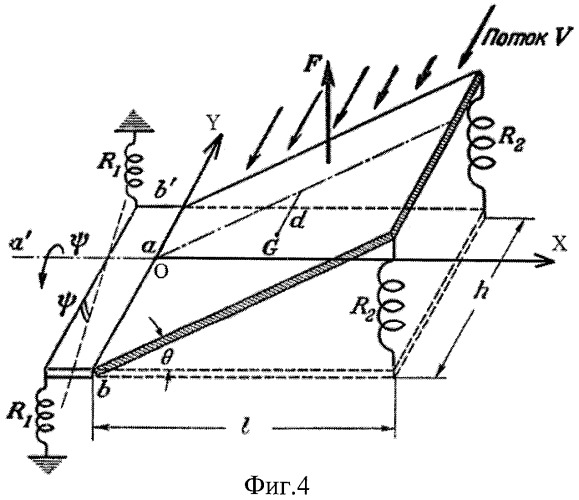
на фиг.4. - Расчетная схема;

на фиг.5. - Схема приложения подъемной силы;

При воздействии на упруго опертую жесткую пластину дозвукового потока воздуха происходят колебания как системы с двумя степенями свободы, зависящие от многих параметров, таких как собственный частоты изгибных и крутильных колебаний, положение центра жесткости, положение центра тяжести, скорость набегающего потока и д.р. (см. И.Рокар. Неустойчивость в механике. - М.: Издательство иностранной литературы 1959. 289 с., с.80)

В данной работе предлагается использовать частотный метод для решения задачи о колебаниях жесткой упруго опертой пластины в дозвуковом потоке газа, с учетом рассеяния энергии при нагружении, с учетом всех вышеперечисленных факторов, с целью определения постоянных времени формирования пограничного слоя.

При рассмотрении тела, погруженного в вязкую жидкость или газ, можно наблюдать следующее характерное для такого рода нестационарных процессов явление. Пограничный слой образуется не мгновенно, а требует на свое развитие конечного промежутка времени, сравнимого по величине с характерным для данного движения временем, потребным для прохождения телом пути, равного размеру тела (см. Лойцянский Л.Г. Ламинарный пограничный слой / Л.Г.Лойцянский // М.: Государственное издательство физико-математической литературы. - 1962. - 480 с., с.114).

Рассмотрим уравнения динамики вязкоупругой системы в операторной форме:

где σ, u - обобщенные силы и перемещения, f - вектор функция; характеризующая силовое воздействие на упругую систему, R - оператор распределенных масс, С - оператор, характеризующий распределение упругих сил, Т - оператор внешнего рассеяния энергии, C₁ - оператор внутреннего рассеяния энергии, t - время, D и D* - дифференциальные операторы, сопряженные в смысле Лагранжа.

Уравнение для силового воздействия f=f(е), нелинейно зависящего от некоторого параметра e, возьмем в виде:

где е=е(α,t) - управляющее воздействие, зависящее от угла атаки, α - пространственная координата, с₁ - оператор обратных связей по перемещению, с₂ - оператор обратных связей по скорости, h - положительно определенная симметричная весовая матрица управляющих воздействий.

Пограничный слой является нестационарным и в самом простейшем виде нестационарность учитывается уравнением (3).

Если исключить из уравнения динамики обобщенные силы σ, то получим уравнение в обобщенных перемещениях:

где B=T+DC₁D* и K=DCD* - положительно определенные, вполне непрерывные операторы рассеяния энергии и упругости.

Рассмотрим уравнения движения упруго опертой жесткой пластины, данные в работе (И.Рокар. Неустойчивость в механике. - М.: Издательство иностранной литературы 1959, 289 с.):

где J₁ и J₂ осевые моменты инерции пластины, J₁₂ - центробежный момент инерции пластины, θ - угол отклонения при изгибе, ψ - угол отклонения при кручении, ω₁ - собственная частота изгибных колебаний, ω₂ - собственная частота крутильных колебаний, ρ₀ - плотность воздуха, h - ширина пластины, l - длина пластины, V - скорость набегающего потока, , (C_z=4÷5).

Для рассматриваемого случая:

где γ - коэффициент рассеяния энергии,

j - мнимая единица;

i- угол атаки.

Тогда уравнение (2) запишется в виде (4)

Относительно сделаем предположение:

е - эффективный угол атаки; е переходит в ψ по окончанию переходного процесса. - скорость перехода к установившемуся значению.

c₂=0, c₁=β

Тогда уравнение (3) можно записать в следующем виде

где , τ - время формирования пограничного слоя

Сделаем замену переменных: u₁=u; . Тогда уравнение (4) можно записать так:

,

Рассмотрим функционал Ляпунова:

Функционал V является положительно определенным. Его производная в силу уравнений движения (7):

Если бы была знакоопределенной отрицательной величиной, то движение было бы асимптотически устойчиво. Первое слагаемое в формуле (9) отрицательно определенное, поэтому достаточно, чтобы:

Это выражение позволяет сформировать критерий устойчивости, который строится по форме этого выражения (10) (Санкин Ю.Н. Частотный критерий устойчивости нелинейных замкнутых систем, включающих вязкоупругое звено с распределенными параметрами / Ю.Н.Санкин // Труды СВМО, 2005, Т.7, №1 / УДК 621.9-05).

Построим передаточную функцию амплитуд крутильных колебаний W_ψ(jω). Для этого в уравнения движения упруго опертой жесткой пластины (5) введем рассеяние энергии, путем умножения членов, содержащих жесткость на (1+jγ), где γ - коэффициент рассеяния энергии.

Возмущающее воздействие приравнивается к единице.

Решение будем искать в виде θ=θ₁sin(ωt+φ), ψ=ψ₁sin(ωt+φ)

Получим систему:

При изменении ω от 1 до 10000 рад/с получим АФЧХ амплитуд изгибных колебаний (фиг.1) и АФЧХ амплитуд крутильных колебаний (фиг.2).

Известно, что каждому витку АФЧХ соответствует один член ряда в разложении по форме колебаний. Между экстремальными точками АФЧХ и коэффициентами соответствующих членов ряда существует однозначная связь, которая используется в настоящей работе для осуществления обратного преобразования Лапласа.

В формуле

- коэффициент усиления;

, - постоянные времени.

В рассматриваемом случае доминирующими являются два витка АФЧХ, поэтому достаточно двух членов ряда разложения по формам колебаний (13). Это в свою очередь означает, что система ведет себя как система с двумя степенями свободы (Санкин Ю.Н. Динамические характеристики вязкоупругих систем с распределенными параметрами / Ю.Н.Санкин // Саратов: Издательство Саратовского университета. - 1977. - 312 с.).

Зависимость (1+jω)·W_ψ(jω) дана на фиг.3:

По этой зависимости определяем крайнее левое пересечение с действительной осью.

Для экспериментального определения критической скорости флаттера (V_k) рассматривается модель установки пластины и обтекания из работы (И.Рокар. Неустойчивость в механике. - М.: Издательство иностранной литературы. 1959. 289 с., с.80).

Тонкая упруго опертая жесткая пластина установлена так, как показано на фиг.4. Пластина может:

1. Поворачиваться на угол ψ вокруг горизонтальной оси aa′, причем образуется угол атаки ψ по отношению к потоку, имеющему скорость V и движущемуся в указанном на фигуре направлении. Две пружины R₁ препятствуют повороту на угол ψ.

2. Поворачиваться на угол θ вокруг оси bb′, перпендикулярной к aa′, две пружины R₂ препятствуют повороту на угол θ.

Угловое премещение θ моделирует изгиб крыла, а угловое перемещение ψ - кручение.

Ось aa′, относительно которой происходит кручение, проходит на расстоянии d впереди центра тяжести G пластины («впереди» - значит в направлении против потока).

Направим ось ОХ по оси aa′, а ось OY по оси bb′, которую примем также проходящей через точку a.

Пусть координаты центра тяжести будут (х₀,y₀). Угол ψ считается положительным, если пластина поворачивается против часовой стрелки, угол θ положителен при подъеме пластины. При таком выборе осей y₀=d будет отрицательным, если центр тяжести G находится позади оси кручения.

Равнодействующая возникающей подъемной силы приложена в точке с абсциссой x=l/2 в середине пластины, расположенной на расстоянии 0,25h от входной кромки (см. фиг.5).

Для простоты предположим, что ось aa′ проходит на расстоянии фокуса. Тогда сила F, приложенная в точке на этой оси, не будет создавать момента, который мог бы дополнительно закручивать упруго опертую жесткую пластину. Но в тоже время эта сила будет давать момент F·l/2, стремящийся изогнуть упруго опертую жесткую пластину в сторону положительных θ, когда F, т.е. угол ψ, имеет положительное значение.

Определим критическую скорость флаттера (V_k) с использованием датчика перемещений (вибраций), установленного на пластине, и осциллографа, подключенного к цепи измерения, содержащей датчик перемещений (вибраций).

Следовательно, из соотношения (6) и (11) следует:

После чего уравнение нестационарного пограничного слоя записывается в виде: . В пределе f(e)=τα′ψ.

Способ определения постоянных времени формирования пограничного слоя, заключающийся в том, что упруго опертую жесткую пластину помещают в дозвуковой поток газа, отличающийся тем что формируют нелинейный частотный критерий устойчивости, выражающийся формулой: ,где h - положительно определенная симметричная весовая матрица управляющих воздействий;j - мнимая единица;ω - круговая частота;W_ψ(jω) - передаточная функция амплитуд крутильных колебаний,а затем определяют критическую скорость флаттера с использованием датчика перемещений, установленного на пластине, и осциллографа, подключенного к цепи измерения, содержащей датчик перемещений, и после чего постоянные времени формирования пограничного слоя определяют по формуле: ,где ρ₀ - плотность воздуха;h - ширина пластины;l - длина пластины;V_k - критическая скорость флаттера.