Способ выравнивания хроматограмм пептидных смесей

Способ выравнивания хроматограмм пептидных смесей

Иллюстрации

Показать все

Реферат

Изобретение относится к методам анализа биологических материалов и может быть использовано для диагностических целей в медицине, ветеринарии и других областях, где необходим анализ сложных биологических смесей.

Масс-спектрометрия (МС), совмещенная с высокоэффективной жидкостной хроматографией (ВЭЖХ), является одним из основных методов идентификации пептидов в протеомных исследованиях. Наиболее распространенным подходом к такой идентификации пептидов в сложных смесях (гидрализате белковой смеси, например) является метод тандемной масс-спектрометрии, основанный на использовании белковых баз данных для сравнения экспериментально полученных масс фрагментов пептидов с теоретически возможными массами фрагментов пептидов белков из баз данных. При таком анализе используется только информация о массе пептида; ВЭЖХ используется лишь для разделения пептидов во времени элюирования по гидрофобности, необходимого из-за большого количества компонентов смеси с близкими массами. Разделение во времени также увеличивает динамический диапазон эксперимента в целом, так как в пределах одного спектра динамический диапазон современных масс-спектрометров ограничен 10⁴, и разнося интенсивные ионы с малоинтенсивными во времени, мы увеличиваем вероятность детектирования небольших пиков в спектрах.

Так как аминокислотная последовательность (сиквенс) пептида влияет на время удержания его в хроматографической колонке, то информация о времени является дополнительной к информации о массе самого пептида и его фрагментов - это дополнительное измерение, которое дает несколько новых возможностей:

а) повысить надежность идентификации пептида;

б) понизить требования на точность измерения масс у масс-спектрометра;

в) идентифицировать пептиды лишь по точной массе (целого пептида, но не его фрагментов) и времени удержания в хроматографической колонке [1].

Последняя из перечисленных возможностей является основой метода точной массово-временной метки (АМТ). При его использовании возникает необходимость сравнения времен хроматографического удержания идентифицируемых пептидов. Небольшие изменения в потоке мобильной фазы, длине хроматографической колонки, изменения в плотности набивки колонки приводят к сдвигу этих времен. Это далеко не полный список факторов, приводящих к этому нежелательному эффекту ([2]).

Одним из часто применяемых способов нормирования хроматограмм является подбор линейной или кусочно-линейной функции, которая, будучи применена к временам удержания в одном хромато-масс-спектрометрическом эксперименте (LC-MS эксперименте), максимизирует их корреляцию с временами из какого либо другого эксперимента, что, однако, не гарантирует, что коррелировать будут одинаковые пептиды в разных экспериментах. Также, например, используются генетические алгоритмы для оптимизации (подбора) коэффициентов линейного уравнения, минимизирующие отклонения времен удержания определенных пептидов, что требует выбора пептидов, используемых для нормализации, заранее. Можно использовать и все пептиды, но это требует гораздо больше времени вычислений [3]. Простое линейное выравнивание времен удержания методом наименьших квадратов, уменьшающее при помощи линейной калибровки отклонения времен выхода ионов с одинаковыми массами, подвержено сильному влиянию шума (случаи, когда массы ионов близки (лежат в пределах точности измерения масс используемого масс-спектрометра) или совпадают для разных пептидов) - каждая точка имеет квадратичный вес в нормировке, а следовательно, каждая точка, выпадающая из линейного тренда, может сильно повлиять на итог.

Учитывая это, нами предложен новый способ выравнивания хроматограмм в хромато-масс-спектрограммах, обладающий высокой устойчивостью к зашумленности данных.

При этом предлагаемый нами способ базируется на следующих представлениях.

При любом алгоритме выравнивания хроматограмм главную проблему представляют пики, соответствующие близким по массам ионам. При отсутствии такой неоднозначности сопоставления пиков всегда можно безошибочно подобрать функцию нормировки. Так как в реальных экспериментах не достигается необходимая для однозначного сопоставления пиков точность измерения масс, используется нижепредлагаемый алгоритм для выделения группы соответствующих пиков из обеих хроматограмм.

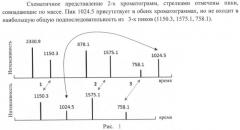
В высокоэффективной жидкостной хроматографии времена удержания молекул (здесь и далее мы будем говорить о пептидах в качестве хроматографируемых образцов) в колонке линейным образом зависят от таких параметров, как скорость потока мобильной фазы, величины градиента концентрации растворителя, длины самой колонки, которые могут варьироваться от эксперимента к эксперименту. Это означает, что порядок выхода пептидов из колонки не должен меняться от эксперимента к эксперименту и от образца к образцу. Следовательно, при отборе пептидов, по которым будет производиться нормировка времен, задача сводится к нахождению наибольшей общей подпоследовательности времен элюирования. Пики, содержащиеся в ней, с большей вероятностью соответствуют одинаковым пептидам в разных экспериментах (например, наибольшей общей подпоследовательностью двух строк 'ABCDABCD' и 'BCDECG' будет строка 'BCDC'). На рис.1 приведен пример хроматограмм с наибольшей общей подпоследовательностью из 3-х совпадающих по массам пиков и одним пиком (1024.5), хотя и совпадающим по массе, но выбивающимся из последовательности.

При такой постановке задачи не учитывается точность совпадения масс для 2-х пиков, а лишь задается пороговое значение для целевой функции ошибки измерения масс, но имеется возможность производить поиск общей подпоследовательности сразу в нескольких хроматограммах. При учете величины точности задача сводится к более сложной проблеме нахождения наидлиннейшего пути на направленном нециклическом графе и имеется возможность сравнить максимум две хроматограммы.

Для решения задач о наибольших общих подпоследовательностях необходимо использовать метод динамического программирования. Суть его заключается в построении матрицы с последующим нахождением в ней маршрута наибольшей длины. Алгоритм построения матрицы прост: по горизонтали откладываются массы из одной хроматограммы, отсортированные по времени элюирования, по вертикали массы из второй хроматограммы, отсортированные тем же образом. На пересечении строки и столбца ставится значение некоторой функции точности совпадения масс, например сигмоиды или ступенчатой функции для задания порога отсечения пиков, не совпадающих по массе (пример такой матрицы приведен в таблице 1).

Таблица 1
Построение матрицы соответствий масс, которая поможет нам найти наибольшую общую подпоследовательность. Для наглядности нули в матрице заменены пустыми ячейками.

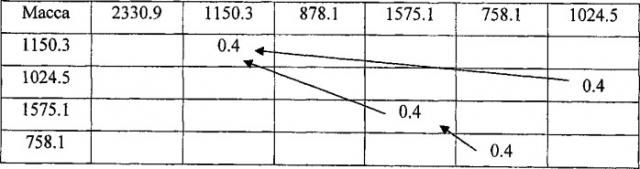
Целью процедуры является обход матрицы, начиная с верхнего левого угла, таким образом, чтобы сумма значений в ячейках на пути была максимальной. При этом на каждом шаге необходимо смещаться минимум на одну клетку вправо и на одну клетку вниз относительно текущей позиции. Алгоритмы поиска таких путей известны, например, можно (как показано в таблице 2) составить еще одну матрицу, назовем ее Т, заполняя каждую ячейку по следующим правилам:

где i - номер строки, j - номер столбца, T_0,j=T_i,0=0 для любых i, j и func(Δm) - целевая функция разности масс соответствующих пиков в спектрах.

Таблица 2
Схематичная иллюстрация матрицы Т, используемой в алгоритме обратного обхода матрицы соответствий масс
Масса	2330.9	1150.3	878.1	1575.1	758.1	1024.5
1150.3	0	0.4	0.4	0.4	0.4	0.4
1024.5	0	0.4	0.4	0.4	0.4	0.8
1575.1	0	0.4	0.4	0.8	0.8	0.8
758.1	0	0.4	0.4	0.8	1.2	1.2

Для нахождения наибольшей общей подпоследовательности требуется обойти матрицу Т в обратном направлении, начиная в правом нижнем углу. На каждом шаге разрешается смещаться на одну клетку влево, вверх или по диагонали, двигаясь в направлении наименьшего изменения значений в ячейках матрицы. Если все окружающие значения одинаковы, то делается шаг по диагонали, а в случае, когда при этом значения в текущей ячейке, в той, куда сделан шаг, различаются, соответствующие массы добавляются к наибольшей общей подпоследовательности. Если достигнута левая либо верхняя граница матрицы, шаги продолжаются в единственном оставшемся допустимом направлении. Когда обход закончен, получившуюся последовательность следует обратить, так как при построении она записывается в обратном порядке, начиная с конца. Таким образом, для матрицы Т из таблицы 2 находим наибольшую общую подпоследовательность элюирования (1150.3; 1575.1; 758.1).

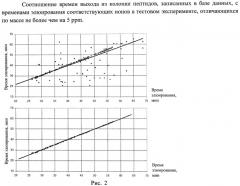
Было проведено сравнение качества нормировок, полученных для одного и того же эксперимента, при сравнении его с нашей базой данных, нормировка была линейной и проводилась по методу наименьших квадратов. По рисункам 2а и 2б видно, насколько эффективно прошла фильтрация данных, автоматически отобранные точки лежат на почти идеальной прямой. В первом случае (рис.2а) отобраны все пики из хроматограммы, совпадающие с записями в базе данных с точностью 5ppm или меньше, уравнение нормировки

t₂=0.89*t₁+3.7, коэффициент корреляции R=0.777

После фильтрации данных методом наибольшей общей подпоследовательности времен элюирования

t₂=0.98*t₁+0.8, коэффициент корреляции R=0.999

Таким образом удается выделить тренд почти идеальной линейной корреляции между множеством экспериментов в базе данных и тестовым экспериментом, проведенным с образцом той же природы, улучшив точность нормировки более чем на 20%, что немаловажно, учитывая тот факт, что, например, в методе точных массово-временных меток при сопоставлении времен выхода из колонки часто используют окно допущения в 3-5% от общего времени эксперимента.

Проверка разработанного метода была осуществлена при исследовании протеома мочи.

Пример

Пробоподготовка

Были собраны образцы мочи от здоровых людей, отцентрифугированы при 2000 g в течение 10 минут. 15 мл надосадочной жидкости из каждого образца концентрировали центрифугированием через фильтр Amicon Ultra Ultracel-15 при 1000 g до объема 500 мкл, полученный концентрат упаривался в лиофильной сушке. Осадок растворялся в буфере для восстановления (0,2 М Tris-HCl, pH 8,5, 2,5 мМ ЭДТА, 8М мочевина) до концентрации белка 10 г/л. Осуществлялось восстановление цистеиновых остатков в белках, алкилирование SH-групп, очистка переосаждением. Затем проводился трипсинолиз полученной белковой фракции мочи для получения итоговой пептидной смеси, готовой для хромато-масс-спектрометрии. Все реагенты покупались у Sigma-Aldrich (США), если не указано иначе.

Хромато-масс-спектрометрия

Эксперименты проводились на нано-ВЭЖХ-МС/МС системе, состоящей из хроматографа Agilent 1100 (Agilent Technologies Inc., Санта-Клара, США) и гибридного масс-спектрометра LTQ-FT Ultra (Thermofisher, Бремен, Германия) - масс-спектрометр ионного циклотронного резонанса (ИЦР), совмещенный с линейной квадрупольной ионной ловушкой, использующейся для накопления ионов и измерения спектров столкновительной фрагментации (МС/МС) ионов. Для хроматографии использовалась колонка ([6] Ishihama et al. 2002) с внутренним диаметром 75 мкм, набитая обращенной фазой ReproSil-Pur С18, диаметр частиц 3 мкм, диаметр пор 100 Å (Dr. Maisch GmbH, Аммербух-Энтринген, Германия). В качестве мобильной фазы (растворителей) использовались (A) вода (с добавлением 0.1% трифторуксусной кислоты) и (B) ацетонитрил.

Проводилась градиентная хроматография с линейным увеличением относительного содержания растворителя B в потоке от 5% до 50% за 90 минут, после каждого эксперимента система промывалась 95% ацетонитрилом в течение 15 минут, а затем 100% растворителем А еще 5 минут. Измерения масс-спектров продуктов хроматографии производились в диапазоне от 300 до 2000 m/z.

Анализ хромато-масс-спектрограмм

Хромато-масс-спектрограммы преобразовывались в списки моноизотопных масс и времен удержания в хроматографической колонке при помощи программы Hardklor [7], эти списки затем обрабатывались программой Kronik (), сворачивающей записи о продолжительно элюирующих пептидах в одну запись с указанием времени хроматографического максимума. Результирующие списки масс/времен сравнивались вышеописанным методом с имеющейся у нас базой данных, составленной по более чем 200 экспериментам с образцами мочи от 18 людей.

Таким образом, предложен новый способ, позволяющий нормировать данные как 2-х, так и большего количества экспериментов. Он может применяться для выравнивания хроматограмм, полученных в разных лабораториях на различном оборудовании, однако в таких случаях может возникнуть необходимость нелинейных или кусочно-линейных нормировок. Теоретически способ также может быть применен для фильтрации данных, полученных при анализе образцов различной природы, при условии наличия в них некоторого количества одинаковых белков (например, мажорных, таких как альбумин).

СПИСОК ЛИТЕРАТУРЫ

1. Angela D. Norbeck, Matthew E. Monroe, Joshua N. Adkins, Kevin K. Anderson, Don S. Daly and Richard D. Smith // Journal of the American Society for Mass Spectrometry. 2005. Vol.16, Issue 8, 1239-1249.

2. Krokhin O.V. // Analitycal Chemistry. 2006. V.78, 7785-7795.

3. Konstantinos Petritis, Lars Kangas, Patrick Ferguson, Gordon Anderson, Ljiljana Paša-Tolić, Mary Lipton, Kenneth Auberry, Eric Strittmatter, Yufeng Shen, Rui Zhao, Richard D. Smith // Analytical Chemistry. 2003. Volume 75, Issue 5, p.1039-1048.

4. D.S.Hirschberg // Journal of the ACM. 1977. V.24, 664.675.

5. Ishihama Y, Rappsilber J, Andersen JS, Mann M. // Journal of Chromatography A. 2002. V.979, 233-239.

6. Hoopmann MR, Finney GL, MacCoss MJ // Analitycal Chemistry. 2007. V.79, 5630-5632.

Способ выравнивания хроматограмм пептидных смесей, включающий отбор образца от биологического объекта, подлежащего исследованию, получение пептидной смеси, готовой для хромато-масс-спектрометрии, проведение хромато-масс-спектрометрии, сравнение полученной хроматограммы с эталонной и нахождение наиболее общих подпоследовательностей, при этом нахождение наиболее общих подпоследовательностей осуществляют следующим образом: проводят построение матрицы, по горизонтали которой откладываются массы из одной хроматограммы, отсортированные по времени элюирования, по вертикали - массы из второй хроматограммы, отсортированные тем же образом, на пересечении строки и столбца ставится значение функции точности совпадения масс для задания порога отсечения пиков, не совпадающих по массе, далее начинают обход матрицы, начиная с правого нижнего угла, на каждом шаге разрешается смещаться на одну клетку влево, вверх или по диагонали, двигаясь в направлении наименьшего изменения значений в ячейках матрицы, если все окружающие значения одинаковы, то делается шаг по диагонали, а в случае, когда при этом значения в текущей ячейке, в той, куда сделан шаг, различаются, соответствующие массы добавляются к наибольшей общей подпоследовательности, если достигнута крайняя левая, либо верхняя граница матрицы, шаги продолжаются в оставшемся допустимом направлении, после окончания обхода получившуюся последовательность необходимо записать в обратном порядке, начиная с конца.