Способ определения массы и координат центра масс тела в заданной плоскости

Способ определения массы и координат центра масс тела в заданной плоскости

Иллюстрации

Показать все

Реферат

Цель изобретения - расширение номенклатуры объектов и повышение точности измерения.

Известен способ определения массы, координат центра масс и центрального момента инерции тела в заданной плоскости по значениям периода собственных крутильных колебаний, измеряемых для различных позиций тела на платформе. По значениям периода рассчитывают центр масс, координаты центра масс и центральный момент инерции тела (авт. св. №1046633, БИ №37, 1983 г.).

Недостатком способа является не учет способности исследуемого образца, закрепленного на платформе, обладать колебательными свойствами. Упругость и инертность элементов конструкции образца придают ему свойства самостоятельной крутильной колебательной системы, присоединенной к платформе, которая совершает собственные крутильные колебания. В результате взаимодействия колебательных систем искажается закон движения платформы как чувствительного элемента измерительной системы.

Кроме этого, подлежащий измерению интервал времени - это величина, в которой скрадывается частотный состав суммарных крутильных колебаний платформы. Невозможно разделить (фильтровать) колебания платформы и собственные крутильные колебания образца на платформе. Их взаимное влияние приводит к динамическим погрешностям измерения интервалов времени. Образцами, обладающими указанными свойствами, могут быть тонкостенные корпусные детали, конструкции пространственных ферм, объекты зоологической природы. Невозможность регулировать динамические нагрузки, воздействующие на образец в процессе измерения, могут приводить к деформации пространственных форм самого образца. В целом, это объекты, для которых модель "твердого тела" применима с ограничениями.

Наиболее близким по технической сущности является способ определения величины и фазы дисбаланса тела в поле центробежных сил, имеющих знакопостоянный характер по направлению и величине и легко регулируемых по величине путем изменения скорости вращения объекта (патент №2237878, БИ №28, 2004 г.).

Однако этот способ не отвечает на вопрос о величине массы и положении центра масс, а позволяет определить только величину произведения массы образца на радиус-вектор центра масс. Каждый из сомножителей в отдельности остается неизвестным. Величина произведения при этом известна, поскольку известна масса пробного груза и радиус установки пробного груза [1, 2].

Цель изобретения - определить массу и радиус-вектор центра масс тела.

Цель достигается за счет того, что измеряются три последовательные интервала времени для каждой из двух известных на платформе позиций каретки массой m с закрепленным на ней исследуемым телом, а по интервалам определяются соответствующие радиус-векторы смещения платформы. По величинам этих радиус-векторов, массе каретки и радиус-вектору положения каретки на платформе рассчитываются масса и координаты центра масс тела. Собственная масса m каретки здесь играет роль пробного груза.

Проведенный заявителем анализ уровня техники, включающий поиск по патентным и научно-техническим источникам информации, позволил установить, что заявителем не обнаружен аналог, характеризующийся признаками, идентичными всем существенным признакам заявленного изобретения.

Следовательно, заявленное изобретение соответствует требованию "новизна" по действующему законодательству.

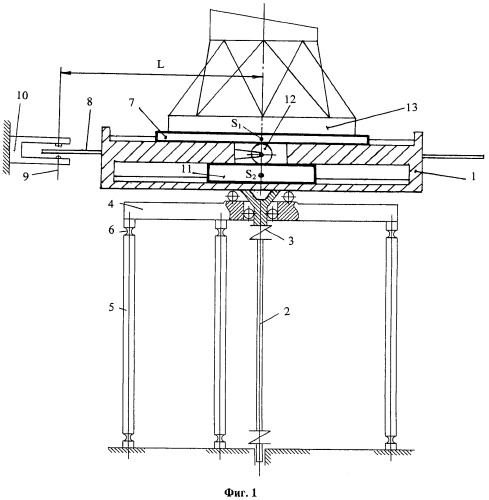
Способ осуществляется следующим образом. Вращение платформе 1 (Фиг.1) сообщается от двигателя через вал 2 с двойным карданным шарниром 3, который не вносит кинематической погрешности по углу поворота. Платформа 1 вместе с основанием 4, тремя стойками 5 и упругими шарнирами 6 образуют колебательную систему типа астатического маятника. Подробная работа стенда, процедура измерения интервалов времени и алгоритмы расчета радиус-вектора приведены в [2] и полностью аналогичны прототипу. Каретка 7 известной массы m может перемещаться и фиксироваться в прямолинейных направляющих, проходящих через ось симметрии вала 2, совпадающую с началом подвижной системы координат Oξ₁η₁, связанной с платформой 1. Ортогональные координатные оси ξ₁ и η₁ расположены на прозрачном носителе 8. При вращении платформы они пересекают оптическую ось 9 датчика 10, расположенного на расстоянии L от оси вала 2. Смещение каретки от оси вала 2 и начала координат всегда может быть определено устройством (не показано). Под кареткой по аналогичным направляющим перемещается уравновешивающий груз 11, массой m, равной массе каретки. Груз предназначен для уравновешивания центробежной силы от действия каретки, если она смещена от начала координат Oξ₁η₁. Перемещение груза 11 в противоположную сторону на равное с кареткой расстояние осуществляется двойной зубчатой реечной передачей, элементами которой служат каретка 7, уравновешивающий груз 11 и два зубчатых колеса 12, расположенных на одной оси и способных блокироваться и разъединяться за счет их взаимного смещения вдоль оси вращения, не выходя из зацепления с рейками. Одно колесо всегда в зацеплении с рейкой на каретке, другое - с рейкой на уравновешивающем грузе 11 (подробно механизм не показан). Находясь в центральном положении, центры масс каретки S₁ и груза - S₂ находятся в начале системы координат и уравновешены. Неуравновешенность всей подвижной системы возможна только из-за смещения центра масс исследуемого тела 13. Пусть этот неизвестный радиус-вектор равен R₁ в координатах Oξ₁η₁, а неизвестная масса тела равна М (Фиг.2).

Вращение платформы 1 с частотой Ω вызовет появление центробежной силы F₁, равной F₁=Ω²МR₁.

Действие силы F₁ вызовет смещение платформы 1 на радиус-вектор r₁. Фазовый угол γ отставания вектора r₁ от R₁ всегда постоянный при постоянных Ω и М. Величина и положение радиус-вектора r₁ с полярным углом β₁ определяются по трем интервалам времени в системе координат Oξ₁η₁ по известному алгоритму. Платформа останавливается.

Каретка 7 с закрепленным на ней телом 13 смещается по направляющим на произвольный, но известный радиус-вектор k, направление которого определено направляющими, и совпадает с координатной осью η₁. Уравновешивающий груз 11 смещается при этом в противоположную сторону на величину k (Фиг.3). Центр масс тела 13 занял новое положение, определяемое неизвестным радиус-вектором R₂=R₁+k (Фиг.2). Соответствующая центробежная сила равна F₂=Ω²МR₂. Она вызовет смещение платформы на радиус-вектор r₂ с полярным углом β₂. Эти координаты находятся по измеренным интервалам времени. Платформа останавливается.

Зубчатые колеса 12 разъединяются между собой и уравновешивающий груз 11 возвращается в исходное центральное положение. Каретка 7 с телом 13 остались в прежнем положении.

При вращении платформа испытывает одновременно действие двух центробежных сил. От неуравновешенной каретки сила F₃=Ω²mk. Направление и величина этой силы известны, т.к. известны m и k (Фиг.2). От действия этой силы смещение платформы составляет вектор r₃. Угол отставания вектора r₃ от вектора k тот же, т.е. γ. Величина и направление этого вектора пока неизвестны, поскольку неизвестен γ и коэффициент динамичности λ измерительной колебательной системы.

Вторая сила - это центробежная сила F₂, а реакция от ее воздействия на динамическую систему - уже известный радиус-вектор r₂. Результирующее смещение платформы от действия двух сил равно вектору r: r=r₂+r₃.

Вектор r и его полярный угол β в системе координат Oξ₁η₁ находится по измерениям трех интервалов времени.

Известные величины r, r₁, r₂, β, β₁, β₃, масса m и величина вектора k позволяют однозначно определить массу М тела и координаты центра масс в плоскости каретки в системе координат Oξ₁η₁.

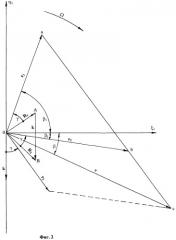
Действительно, Δ ОАВ подобен Δ oab. Это следует из того, что векторы r₁ и ₂ отстают от векторов R₁ и R₂ на один и тот же угол γ. Отсюда следует, что ΔОАВ повернут на угол γ относительно Δoab. Сторона ab в Δ oab находится по теореме косинусов .

Из подобия указанных треугольников следует .

Угол фазового отставания γ определяется из скалярного произведения известных векторов k и ab .

По известным векторам r₁ и r и углу (β₁+β) между ними находим длину стороны ас в Δоас .

Тогда отрезок bc равен: |bc|=|ас|-|ab|.

Но |bc|=|r₃| по построению как противоположная сторона параллелограмма. Модуль |r₃| определяется только действием известной силы F₃=Ω²m|k|, и существует пропорциональная зависимость между |r₃| и F₃: |r₃|=λΩ²m|k|. Кроме этого, вектор ab - это векторная разность ab=r₂-r₁ и, следовательно, модуль вектора ab определяется только действием дисбаланса М|k|, т.е. |ab|=λΩ²М|k|. Оба равенства для |r₃| и |ab| определяют M .

Таким образом найдены масса М и координаты центра масс - R₁ и β₁ в полярной системе координат в плоскости каретки.

Источники информации

1. Штейнвольф Л.И. Динамические расчеты машин и механизмов. - М.: Машиностроение, 1961. 340 с.

2. Алешин А.К. Метод определения величины и фазы дисбаланса ротора // Проблемы машиностроения и надежности машин. 2006. №6.

Способ определения массы и координат центра масс тела в заданной плоскости, заключающийся в определении радиусов-векторов смещения вращающейся платформы с измеряемым телом, отличающийся тем, что производят измерения трех радиусов-векторов: первый вызван действием только дисбаланса тела, закрепленного в каретке известной массы и способной перемещаться и фиксироваться на платформе; второй - действием дисбаланса тела, смещенного вместе с кареткой на произвольную известную величину; третий обусловлен совместным действием этого же дисбаланса и известного дисбаланса каретки из-за ее смещения от оси вращения, а по трем радиусам-векторам, массе и величине смещения каретки определяют массу тела и координаты центра масс в плоскости каретки.